Teorema lui Pitagora - ce trebuie să știi

Istoric

Ce este o teoremă

Enunțul teoremei lui Pitagora

Un exemplu practic

Reprezentarea geometrică a teoremei lui Pitagora

La școală

Vezi și
 

Istoric

Teorema lui Pitagora este una dintre cele mai cunoscute teoreme din Matematică. Teorema este atribuită lui Pitagora, un matematician din Grecia Antică (c. 570 – c. 495 î.Hr.) deși există unele izvoare istorice care sugerează că aceste lucruri erau cunoscute dinainte de Pitagora. Teorema lui Pitagora este foarte importantă pentru omenire. În timpuri străvechi, teorema lui Pitagora le-a permis strămoșilor noștri să navigheze. Ulterior, pe baza teoremei lui Pitagora oamenii de știință au făcut descoperiri importante în domenii precum cartografia (= știința de a face hărți) și trigonometria (= ramură a matematicii care studiază relația dintre laturile și unghiurile unui triunghi). 

Ce este o teoremă

Este posibil să nu fi auzit cuvântul teoremă foarte des înainte de a învăța despre teorema lui Pitagora. Înainte să discutăm despre teorema lui Pitagora e bine să știm în general ce este o teoremă. O explicație pe înțelesul tuturor este că o teoremă este o afirmație cu conținut matematic. Dar asta nu e tot. Afirmația conținută în teoremă s-a demonstrat prin mijloace matematice că este adevărată. Teoremele sunt importante pentru că ne ajută să înțelegem lucruri noi și să rezolvăm probleme. De aceea trebuie să le înțelegem și să le memorăm.

Enunțul teoremei lui Pitagora

Teorema lui Pitagora stabilește o relație între cele trei laturi ale unui triunghi dreptunghic și sună în felul următor: într-un triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei. Dacă nu știți ce este o catetă și ce este o ipotenuza explicăm pe scurt. Un triunghi dreptunghic conține un unghi de 90 de grade. Cele două laturi alăturate unghiului de 90 de grade se numesc catete în timp ce latura opusă unghiului de 90 de grade se numește ipotenuză.

 

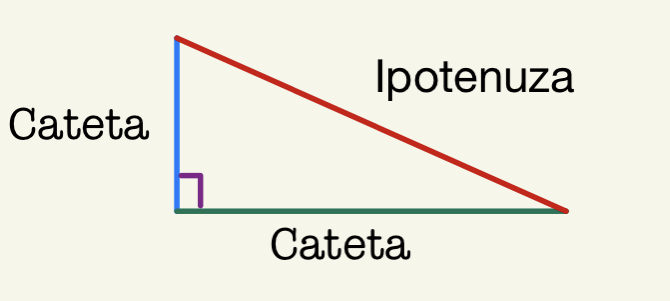
În mod frecvent, catetele și ipotenuza se notează cu litere mici ca în exemplul de mai jos.


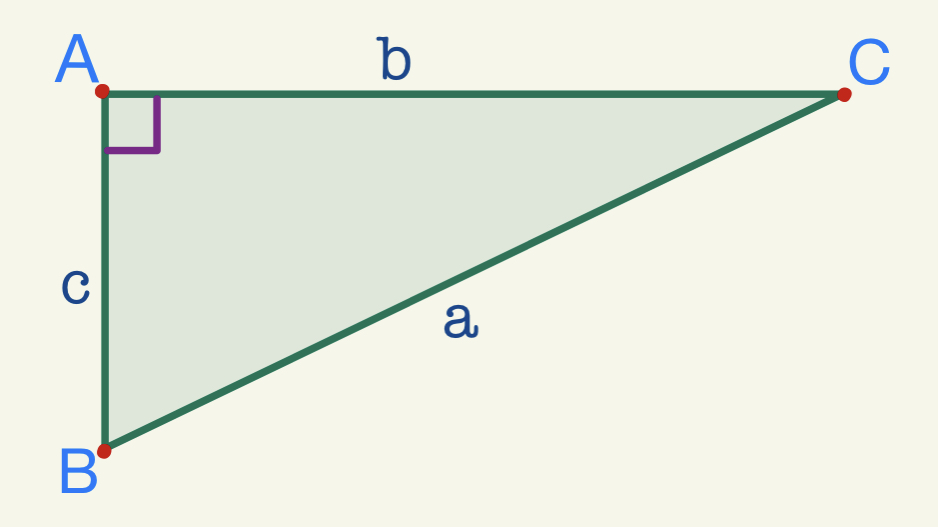
Acest exemplu ne permite să scriem următoarea concluzie:

Pe scurt:

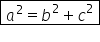
Un exemplu practic

Să presupunem că avem o casă ca în desenul de mai jos și că vrem să tragem un fir electric de la priza din stânga la priza din dreapta imaginii. Deși nu am desenat ne putem închipui că avem pereți interiori și mobilă care nu ne permit să măsurăm direct lungimea acestui fir. Cum altfel am putea face? Evident, putem afla lungimea firului nostru cu ajutorul teoremei lui Pitagora.

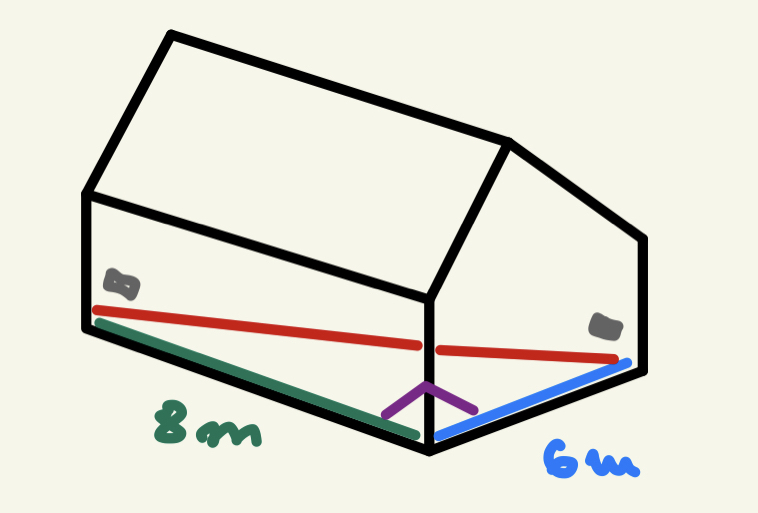
Observăm că muchia casei reprezentată cu albastru are 6 metri și cea reprezentată cu verde are 8 metri și că unghiul format de cele două muchii figurat cu violet este de 90 de grade. Firul nostru va fi reprezentat de segmentul de culoare roșie care reprezintă în același timp ipotenuza. Am reprezentat mai jos aceeași podeau casei și trinunghiul dreptunghic format de cele trei segmente.

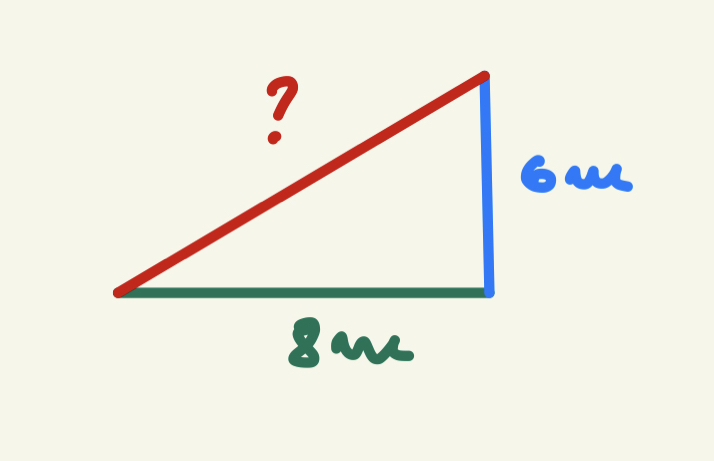
Notăm lungimea firului nostru cu x și aplicând teorema lui Pitagora obținem că:



Prin urmare, lungimea firului nostru este de 10 metri. Nu trebuie să uităm unitatea de măsura. De asemenea, nu uitați că lungimile segmentelor în teorema lui Pitagora sunt la puterea a doua sau la pătrat. Ca să afli de ce lungimile segmentelor din teorema lui Pitagora sunt la puterea a doua și care este legătura cu figura geometrică reprezentată de pătrat citește mai jos.

Reprezentarea geometrică a teoremei lui Pitagora

Se pare că atunci când Pitagora încerca să găsească o demonstrație pentru observațiile sale despre laturile triunghiului dreptunghic, el a văzut o legătură între ariile pătratelor care se pot construi pe baza laturilor unui triunghi dreptunghic. În figura de mai jos am reprezentat la scară aceleași dimensiuni ale triunghiului din problema de mai sus (6 și 8 metri pentru catete și respectiv 10 metri pentru ipotenuză) dar de data aceasta am reprezentat și cele trei pătrate care se pot construi plecând de la acest triunghi dreptunghic.


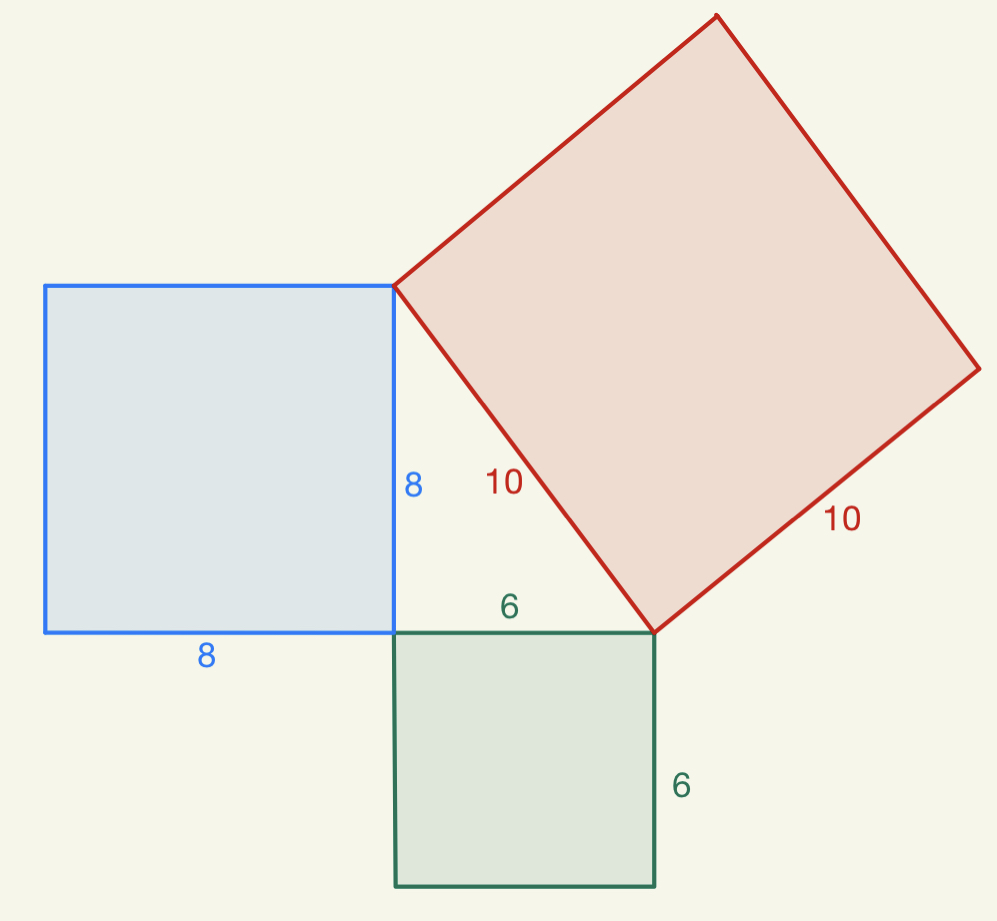
Stim că un pătrat este o figură geometrică, mai bine zis un poligon, în care toate laturile sunt egale (= congruente) și paralele două câte două. Aria unui pătrat se obține înmulțind două laturi între ele sau altfel sus, ridicând lungimea unei laturi la puterea a doua. Spre exemplu, în figura de mai sus:
Pătratul verde are aria de
Pătratul albastru are aria de 
Pătratul roșu are aria de
Observați: Pătratul verde + Pătratul albastru = Pătratul roșu (36cm² + 64cm²=100cm²) sau cu alte cuvinte, suma pătratelor formate de catete este egală cu pătratul format pe baza ipotenuzei.

O altă idee interesantă este că unui segment putem să-i măsurăm lungimea dar un segment considerat de unul singur are o singură dimensiune - lungimea sa. Lungimea unui segment se poate măsura ca fiind 1 milimetru (1 mm), 1 centimetru (1cm), 1 metru ș.a.m.d. Ei bine, spre deosebire de lungimea unui segment care este unidimensională, aria unui pătrat este bidimensională. Adică aria unui pătrat se obține prin înmulțirea a două laturi și de aceea unitate de măsură a ariei este la puterea a doua (1 mm², 1 cm², 1 m²  ș.a.m.d) sau se mai spune și la pătrat.   

La școală
În general, la școală vi se vor da probleme în care fie se cunoaște lungimea catetelor și se cere să se calculeze lungimea ipotenuzei, fie se cunoaște lungimea unei catete și a ipotenuzei și se cere să se calculeze lungimea celeilalte catete. Vă invităm să faceți înlocuirile în figura de mai jos și să vedeți dacă obțineți rezultatele corecte. În primul triunghi se cere calcularea ipotenuzei -  deja am rezolvat mai sus pe pagină acest caz. Vă invităm să faceți înlocuirile în celelalte două exemple și să vedeți dacă puteți calcula corect lungimea catetei mari (cu verde) și a catetei mici (cu albastru).


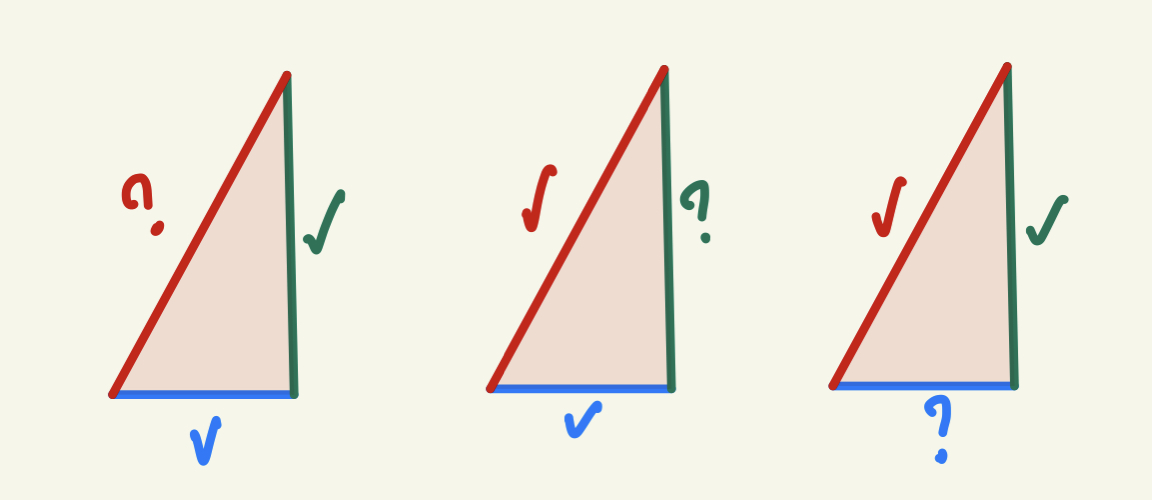
Vezi și
Teorema lui Pitagora - lecție video
Teorema lui Pitagora - exerciții rezolvate