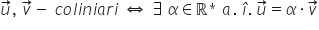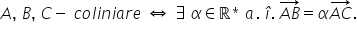Coliniaritatea a doi vectori

în această lecție o să vedem Care

este condiția de coliniaritate

a 2 vectori respectiv condiția

de coliniaritate a 3 puncte doi

vectori sunt coliniari dacă au

aceeași direcție dacă ne uităm

la vectorii a și b observăm că

aceștia au drepte suport paralele

prin urmare a și b sunt vectori

coliniari De asemenea și vectori

c și d sunt coliniare pentru că

au aceeași dreaptă suport în schimb

vectorii A și F nu sunt coliniari

pentru că aceștia nu au aceeași

direcție Așadar doi vectori vor

fi necoliniari dacă dreptele lor

suport sunt concurente în lecția

trecută am văzut că atunci când

înmulțim un Vector cu un scalar

se obține un alt Vector având aceeași

direcție cu vectorul dat aceasta

va fi și condiția de coliniaritate

a 2 vectori Iată vectorii u și

v sunt coliniari Dacă și numai

dacă există un număr real Alfa

pe lângă tu să fie egal cu alfa

ori V în mod asemănător vom scrie

și condiția de coliniaritate a

3 puncte punctele a b și c sunt

coliniare Dacă și numai dacă vectorii

ab și ac sunt coliniari adică există

un scalar Alfa astfel încât ab

să fie egal cu alfa ori ac de fapt

punctele a b și c sunt coliniare

dacă oricare doi dintre vectorii

AB AC sau BC sunt coliniari în

continuare o să facem o aplicație

Fie a b c d un pătrat la punctul

a se cere sa construim punctele

m n p și q astfel încât vectorul

BM să fie egal cu 2 pe 3 ori bc

vectorul AB să fie egal cu 3 pe

2 ori a d și a q să fie egal cu

3 ab iar la punctul b se cere să

demonstrăm că punctele p c și q

sunt coliniare în această prima

relație de ducem că vectorii b

m și b c sunt vectori coliniari

întrucât vectorul BM se obține

Înmulțind vectorul BC cu scalarul

2 pe 3 Așadar punctele b m și c

trebuie să fie puncte coliniare

din moment ce 2 supra 3 este o

fracție subunitară înseamnă că

punctul M va fi situat pe dreapta

BC dar în interiorul segmentului

BC o să mai scriu această relație

încă o dată b m este egal cu 2

pe 3 ori b c această relație se

mai poate scrie și a astfel b m

supra bc Acum ne referim la segmentele

b m și b c egal cu 2 pe 3 Așadar

ca să construim punctul M va trebui

să împărțim segmentul BC în trei

părți egale iar m va fi situat

la două treimi de b și o treime

de ce iartă Aici este punctul M

acum trebuie să construim punctul

p astfel încât ab să fie egal cu

3 pe 2 din ad Așadar vectorii AB

și AD trebuie să fie vectori coliniari

prin urmare punctul P va fi situat

pe dreapta A D din moment ce 3

supra 2 este o fracție supraunitară

înseamnă că punctul pe va fi situat

în exteriorul segmentului ad ne

uităm și la sensul acestor vectori

sensul este de la ei spre de prin

urmare va trebui să prelungim segmentul

ad în sus 3 supra 2 înseamnă un

întreg și 1 pe 2 Așadar prelungim

segmentul ad cu un segment având

lungimea egală cu jumătate din

lungimea segmentului ad Iată aici

va fi punctul p am construit Așadar

punctul p astfel încât modulul

vectorului AB să fie egal cu 3

pe 2 din modulul vectorului ad

și acum trebuie să construim punctul

q astfel încât modulul vectorului

a q să fie egal cu 3 ori modulul

vectorului ab observăm Așadar că

punctele a q și b trebuie să fie

puncte coliniare Deci q va fi situat

pe dreapta ab notăm la sensul vectorului

de la ei trebuie prelungim Așadar

segmentul ab în partea dreaptă

cu un segment având lungimea de

două ori mai mare decât cea a segmentului

AB Aici este punctul q Așadar lungimea

segmentului a q este de trei ori

mai mare decât cea a segmentului

AB Să arătăm acest lucru și pe

figură de stil mentele acestea

sunt congruente la fel și aceste

segmente erau congruente am reușit

așa de astea construim punctul

q astfel încât modulul vectorului

a q să fie de trei ori mai mare

decât modulul vectorului ape și

acum trebuie să arătăm că punctele

p c și q sunt coliniare perfect

pentru a demonstra că punctele

p c și q sunt coliniare trebuie

să arătăm că vectorii CP și cq

sunt coliniari sau c p și q p sau

Q c respectiv q pe ce oricare doi

vectori dintre cei care se formează

cu ajutorul acestor litere trebuie

să fie vectori coliniari vom arăta

că vectorii CP și cq sunt vectori

coliniari pentru aceasta trebuie

să arătăm că are loc următoarea

relație si q este egal cu alfa

ori CP dacă reușim să demonstrăm

că are loc această relație atunci

vectorii sunt coliniari iar punctele

p c și q sunt coliniare Așadar

Haideți exprimăm vectorul c p ne

uităm În triunghiul C pe D observăm

că vectorul c p este egal cu cd

plus de pe Aplicând regula triunghiului

se obține astfel că vectorul c

este suma vectorilor c d și d p

dacă ne uităm acum la vectori cd

și ab observăm că aceștia au aceeași

direcție dar sensuri opuse prin

urmare vectorul CD este egal cu

minus ab iar de pe este jumătate

din ad Așadar vom scrie unu pe

doi ori Ade și acum să exprimăm

și vectorul c q ne uitam în triunghiul

a c b q acest Vector este suma

dintre vectorii c b și b q scopul

nostru este să o exprima un vectorul

c q cu ajutorul vectorului CP Așadar

în exprimarea lui cq va trebui

să regăsim această expresie și

acum si b este egal cu minus a

d pentru că CD și AD sunt vectorii

opuși iar b q este de două ori

mai mare decât ab Deci avem 2ab

adunarea vectorilor este comutativă

prin urmare Putem să scriem 2 ab

minus ad și acum ca să ajungem

la această relație o să îl dăm

factor comun pe minus doi avem

minus 2 pe lângă minus a b plus

1 pe 2 a d observăm acum că expresia

din paranteză este chiar vectorul

c p am arătat Așadar că există

un scalar Alfa Iar acest calar

este minus 2 astfel încât c q să

fie egal cu al fă orice pe DC q

este minus 2 ori c p egal cu alfa

orice prin urmare cei doi vectori

sunt coliniari și atunci punctele

p și q sunt coliniare