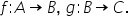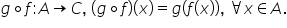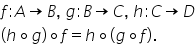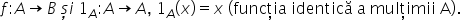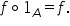Compunerea funcțiilor (teorie)

avem o mulțime A și o altă mulțime

b dacă definim o funcție f de la

a cu valori în b atunci fiecărui

element x din mulțimea A o se corespundă

un unică element în mulțimea B

notat cu ftxf25a Mo altă mulțime

C și definim am o funcție de la

b cu valori în c pe care o Vom

nota cu gem atunci această funcție

Asociază fiecărui element f de

x din mulțimea B un unic element

în mulțimea C notat cu g d e f

de x g d f de x va fi imaginea

elementului fdx prin funcția G

având aceste două funcții F și

G cu ajutorul lor putem să definim

o a treia funcție care duce elementele

din ei direct în mulțimea c iar

această funcție se numește compunerea

funcțiilor g și se notează astfel

și citim G compus cu F atenție

importantă ordinea în care scriem

Mai întâi se scrie a doua funcție

apoi prima observăm că operația

de compunere a două funcții poate

avea loc numai atunci când există

o relație de incluziune sau de

egalitate între codomeniul funcției

f și domeniul funcției G așa dar

având o funcție f definită pe a

cu valori în b și o altă funcție

G definită pe b cu valori în c

iar t cu domeniul funcției f coincide

cu domeniul de definiție al funcției

G atunci în aceste condiții putem

să definim o altă funcție compus

cu F definită pe r cu valori în

c a astfel G compus cu F în punctul

x va fi egal cu g d f d x pentru

orice x din mulțimea A deci x este

element al mulțimii f de x sau

imaginea elementului x prin f este

element din mulțimea b iar g d

e f de x va fi un element din mulțimea

C să reținem că este importantă

această notație mai exact ordinea

în care scriem cele două funcții

pentru că operația de compunere

a două funcții nu este comutativă

o să vedem imediat și un exemplu

așa de edgecam Pascu f nu este

același lucru cu F compus cu g

în continuare o să facem un exemplu

simplu pentru a înțelege mai bine

această operație de compunere A

funcțiilor Avem două funcții F

și G definite astfel e f definită

pe mulțimea formată din elementele

minus 1 0 și 2 cu valori în mulțimea

4 5 6 iar G definită pe mulțimea

4 5 6 cu valori în mulțimea formată

din elementele minus 37 și nouă

din moment ce codomeniul funcției

f este identic cu domeniul funcției

G are loc compunerea G compus cu

F aceasta va fi o funcție definită

pe mulțimea minus 1 0 2 și cu valori

în mulțimea formată din elementele

minus 3 7 și 9 iar G compus cu

f de x egal cu g de f de x și Haideți

să calculăm G compus cu F pentru

fiecare element din domeniul de

definiție începem cu minus 1 g

compus cu F de minus 1 va fi egal

cu g de f de minus 1 Ashley minus

1 este 4 Deci avem g de 4 iar g

de 4 este egal cu minus 3 apoi

Jack compus cu F Calculați în punctul

zero va fi egal cu g de f de 0

f de 0 este 5 prin urmare o să

avem g de 5 egal cu 7 și ce compus

cu F de 2 a fi egal cu g d f de

2 de 2 este egal cu 6 Așadar avem

g de 6 iar g de 6 este egal cu

9 iar eu zic că este destul de

simplă această operație de compunere

a două funcții iar în continuare

aș vrea să amintesc câteva proprietăți

ale acesteia înainte însă trebuie

să definim funcția identică a unei

mulțimi dacă avem o funcție f definită

pe a cu valori în aceeași mulțime

A unde f de x este egal cu x o

astfel de funcție se numește funcție

identică a mulțimii a se va înota

în general astfel un indice a definită

pe a cu valori in A1 indice a d

x egal cu x o notăm astfel pentru

AO diferenția de celelalte funcții

să dăm și un exemplu funcția identică

a mulțimii R calculată în radical

din 2 va fi egal cu radical din

2 Așadar imaginea unui element

prin funcția identică este elementul

respectiv și acum să vedem în continuare

două proprietăți ale compunerii

funcțiilor dacă avem funcția identică

a mulțimii a unde 1A de x este

egal cu x și o altă funcție f definită

pe a cu valori în b atunci f compus

cu funcția identică la fiecare

chiar cu F știu că două funcții

sunt egale dacă ele au același

domeniu același codomeniu și punctuală

funcțiile coincide Haideți să vedem

care ar fi domeniul și codomeniul

acestei funcții f compus cu funcția

identică va fi va avea ca domeniul

de definiție mulțimea A iar codomeniul

acesteia va fi mulțimea B urmare

uitând un a la f compus cu funcția

identică și la funcția f observăm

că ele au același domeniu de definiție

a același codomeniul b iar f compus

cu funcția identică calculată în

punctul x va fi egal cu F d 1 a

b x iar 1 a de x este chiar x Așa

da să reținem că atunci când compunem

o funcție e f cu funcția identică

Rezultatul este chiar funcția f

și o a doua proprietate dacă avem

o funcție f definită pe a cu valori

în b g definită pe r cu valori

în c și h definită pe r cu valori

în d atunci compunere acestor funcții

este o operație asociativă pentru

că a compus cu gem compus cu F

este același lucru cu h compus

cu g compus cu F compunerea funcțiilor

nu este comutativă să vedem un

exemplu avem o funcție f definită

pe r cu valori in R Unde f de x

este egal cu 2 x și g definită

pe r cu valori in r g de x egal

cu x plus 2 observăm că aceste

două funcții au același domeniu

și același codomeniu prin urmare

există G compus cu F și F compus

cu g g compus cu f de x este egal

cu g de f de x pentru a calcula

g d f d x ne uităm la Legea funcției

g g de x este egal cu x plus doi

dar acum noi avem g d e f de x

prin urmare în această formulă

în loc de x o să avem f de x pentru

că acum argumentul funcției este

fdx Așadar va fi egal în continuare

cu f de x plus 2 iar f de x este

egal cu 2x plus doi și acum să

calculăm f compus cu g de x a fi

egal cu F de g de x aceasta este

egală cu 2x argumentul funcției

f în acest caz este gdx Așadar

în loc de x momaie g de x 2 ori

g de x iar g d x este x plus 2

face calculele și obținem 2 x plus

4 și acum îl tendoane la aceste

rezultate putem observa că G compus

cu F nu este același lucru cu F

compus cu g Așadar să reținem că

operația de compunere nu este comutativă

putem să compunem o funcție e f

și cu ea însăși iar pentru această

compunere vom folosi următoarea

notație f compus cu F se notează

astfel f indice superior 2 între

paranteze sau în unele cărți se

folosește și această notație f

cu indice inferior 2 fără paranteze

ia dacă avem f compusă cu ea însăși

de n ori pentru aceasta vom folosi

notația f indice superior n între

paranteze în următorul film o să

facem câteva exerciții pentru a

trage mai bine ai compunerea funcțiilor