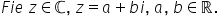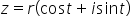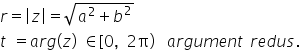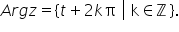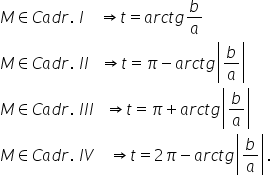Forma trigonometrică a unui număr complex

în această lecție voi prezenta

a forma trigonometrică a numerelor

complexe am văzut că unui număr

complex z de formă a plus b e e

corespunde un Unix punct în plan

numit imaginea geometrică a numărului

complex acest punct pe care îl

am notat cu m va avea coordonatele

a și b unde a este partea reală

iar b este partea imaginară a numărului

complex numerele a și b se numesc

coordonate carteziene dar poziția

punctului m în plan mai poate fi

caracterizată și de alte două elemente

mai întâi de lungimea segmentului

om pe care o voi nota cu aer apoi

de unghiul pe care îl face semidreapta

om cu semiaxa pozitivă a numerelor

reale voi nota acest unghi cute

numerele ieșite se vor numi coordonate

polare Dacă erai este egal cu om

iar o m știind că este egal cu

modulul numărului complex z atunci

va rezulta că r este egal cu radical

din a pătrat plus b pătrat acest

număr ar se numește raza polară

sau raza vectoare numărul de se

numește argumentul redus al numărului

complex det și se notează astfel

3 este egal cu arc z citim argumentul

numărului complex det vom considera

că unghiul t este în intervalul

0 2 pi Deci raza polară a imaginii

lui z este egală cu modulul lui

z iar argumentul polar te al imaginii

lui z se numește argumentul redus

al lui z și se notează în concluzie

Orice număr complex poate fi reprezentat

în plan dacă se cunosc cele două

coordonate polare dacă notez proiecția

punctului m pe axa o x cu A atunci

În triunghiul dreptunghic a o m

Aplicând cosinus de T obținem cosinus

de TE egal cu raportul dintre catetele

tu rată și ipotenuză adică amic

supra R de aici se obține a egal

cu r cosinus de ten dacă aplicăm

sinus de ten avem sinus de TE egal

cu b supra R și obținem b egal

cu r ori sinus de te și acum înlocuim

aceste două valori în expresia

algebrică a numărului complex z

10 este a plus b egal în continuare

în loc de a voi scrie aer cosinus

de T plus e în loc de B avem ursinus

de ten se poate da factor comun

pe r și obținem 10 egal cu r pe

lângă cosinus de T plus e sinus

de ten aceasta este forma trigonometrică

a numărului complex z unde t este

un unghi din intervalul 0 2 pi

Dacă punem în locul lui t valoarea

te plus 2k nu am obține 10 egal

cu a r pe lângă cosinus de te plus

2k plus sinus de te plus doi copii

unde k este un număr întreg însă

funcțiile ce nu și cosinus sunt

periodice având perioada principală

2 pi Așadar cosinus de te plus

doi copii va fi egal cu cosinus

de timp și la fel sinus de T plus

2k este egal cu sinus de ten obținem

Așadar aer pe lângă cosinus de

ten plus e sinus de te și atunci

Orice număr te pentru care este

verificată această relație se numește

argument a lui z mulțimea tuturor

argumentelor numărului complex

z se va nota astfel arg Z egal

cu mulțimea formată din argumentul

redus al numărului complex Z plus

2k unde k este număr întreg Așadar

diferența dintre două argumente

ale unui număr complex nenul este

multiplu întreg de doi fii cu alte

cuvinte dacă raza este constantă

valorile lui t ce diferă prin doi

capii caracterizează același punct

în plan pentru determinarea argumentului

polar trebuie să avem în vedere

cadranul în care este situată imaginea

geometrică astfel dacă m este situat

în cadranul întâi atunci abscisa

este pozitivă și ordonata este

pozitivă dacă imaginea geometrică

a lui z este un punct situat în

cadranul al doilea atunci a este

negativ iar b este pozitiv Dacă

M este situat în cadranul 3 a este

negativ și b este de asemenea negativ

iar dacă m este un punct din cadranul

patrulea atunci abscisa este pozitivă

iar ordonata va fi negativă Haideți

să vedem cum cred câteva exemple

avem numărul complex Z egal cu

1 plus radical din 3 și dorim să

scriem acest număr sub forma trigonometrică

pentru aceasta va trebui să găsim

cele două coordonate polare adică

raza polară și argumentul redus

pentru început am reprezentat în

plan imaginea geometrică a numărului

complex z am obținut punctul M

având coordonatele 1 și radical

din 3 am notat cu a proiecția punctului

m pe axa o x raza polară este lungimea

segmentului o m iar argumentul

redus este unghiul a o m pentru

a găsi raza R vom calcula modulul

numărului complex z și avem radical

din 1 la pătrat plus radical din

3 la pătrat egal cu radical din

4 și egal cu 2 iar pentru a găsi

argumentul te vom aplica în triunghiul

dreptunghic a o m tangentă de te

tangenta este raportul dintre cateta

opusă și cateta alăturată avem

a m supra o a egal cu radical din

3 supra 1 și egal cu radical din

3 Deci tangentă de tei este radical

din 3 noi Trebuie să găsim unghiul

t a cărui tangentă este radical

din 3 pentru aceasta vom folosi

următoarea notație de este egal

cu arc tangentă de radical din

3 despre funcția arctangenta vom

discuta pe larg pentru altă lecție

deocamdată tot ce trebuie să știți

este că această notație se referă

la unghiul a cărui tangentă este

radical din 3 Iar ace Asta este

pi supra 3 pentru că tangență de

pi supra 3 este radical din 3 am

găsit raza polară și argumentul

redus și acum putem să scriem formă

trigonometrică a numărului complex

z z va fi egal cu r pe lângă cosinus

de te plus sinus de ten egal cu

2 pe lângă cosinus de pi supra

3 plus sinus de pi supra 3 aceasta

este forma trigonometrică a numărului

complex Haideți să scriem și argumentul

numărului complex z acesta va fi

mulțimea argumentelor de forma

pe supra 3 plus 2k unde k este

număr întreg putem să facem și

o scurtă verificare pentru a vedea

dacă această formă trigonometrică

Este corectă deci putem să calculăm

mai departe și obținem 2 pe lângă

cosinus de pi supra 3 este 1 pe

2 plus e sinus de pi supra 3 este

radical din 3 pe 2 dacă desfacem

parantezele și simplificăm obținem

întradevăr z t egal cu 1 plus radical

din 3 asa dar forma trigonometrică

la care am ajuns Este corectă să

vedem un alt exemplu avem numărul

complex z de forma minus radical

din 3 plus in am reprezentat în

plan imaginea geometrică și am

obținut punctul M având coordonatele

minus radical din trei și unu observăm

că punctul m este situat în cadranul

al doilea pentru a scrie Acest

număr sub forma trigonometrică

om calculat mai întâi R adică modulul

numărului complex sat și avem radical

din minus radical din 3 la pătrat

plus 1 la pătrat egal cu radical

din 4 și egal cu 2 argumentul redus

al numărului complex z este măsura

în radiani a acestui unghi întotdeauna

Considerăm unghiurile în sens trigonometric

Deci acesta este argumentul te

și mai notez unghiul om cu alfa

folosind această notație putem

scrie că te este egal cu pi minus

Alfa Așadar vom calcula mai întâi

unghiul Alfa apoi unghiul t pentru

a calcula unghiul Alfa în triunghiul

a o m aplicăm tangentă de Alfa

aceasta va fi egală cu a m supra

AO și egal cu 1 supra a o va fi

modul din minus radical din 3 Considerăm

valoarea aceasta în modul deoarece

vorbim despre lungimea laturii

AO egal cu 1 pe radical din 3 și

egal cu radical din 3 pe 3 atunci

Alfa va fi arctangenta de radical

din 3 pe 3 adică unghiul a cărui

tangentă este radical din 3 supra

3 egal cu pi supra 6 este egal

cu pi minus Alfa adică pe minus

pi supra 6 egal cu 5 supra 6 am

găsit raza polară și argumentul

redus în consecință putem să scrie

formă trigonometrică a numărului

complex z va fi egal cu r pe lângă

cosinus de te plus e sinus de TE

egal cu 2 pe lângă cosinus de 5

supra 6 plus e sinus de 5.000 supra

6 Haide să scriem și argumentul

numărului complex z argumentul

lui z va argumentul redus 5 pi

supra 6 plus 2k unde k este număr

întreg continuăm cu un alt exemplu

avem numărul complex Z egal cu

minus 2 minus 2 e Și ne propunem

să scriem acest număr sub forma

trigonometrică am reprezentat în

plan imaginea geometrică a acestui

număr am obținut punctul M având

coordonatele minus 2 minus 2 pentru

a calcula raza polară R vom calcula

modulul numărului complex z și

avem radical din minus 2 la pătrat

plus minus 2 la pătrat egal cu

radical din 4 plus 4 adică radical

din 8 și egal cu 2 radical din

2 argumentul redus este măsura

în radiani a acestui unghi acesta

este argumentul te și dacă nu te

măsura acestui unghi cu alfa atunci

te va fi egal cu pi plus Alfa mai

întâi voi calcula unghiul Alfa

din triunghiul dreptunghic a om

aplicăm tangentă de Alfa și avem

cateta opusă a m supra cateta alăturată

a o egal Considerăm modulul acestor

numere avem modul din minus 2 supra

modul din minus 2 întrucât vorbim

de lungimea laturilor a m respectiv

a și gaz Motan Noir a cu 1 Alfa

va fi arctangenta de 1 unghiul

a cărui tangentă este 1 are măsura

egală cu pi supra 4 Revenim la

3 este egal cu p plus p supra 4

și egal cu 5 supra 4 Deci argumentul

redus este egal cu 5 p supra 4

și atunci forma trigonometrică

a numărului z va fi pe lângă cosinus

de 3 plus sinus de ten egal cu

2 radical din 2 pe lângă cosinus

de 5 p supra 4 plus e sinus de

5 pi supra 4 aceasta este forma

trigonometrica a lui z Putem să

scriem și argumentul lui z vom

avea argumentul redus adică 5 p

supra 4 plus 2k unde k este număr

întreg și să mai vedem un ultim

exemplu am ales de data aceasta

Un punct situat în cadranul 4 Iată

avem numărul complex Z egal cu

2-a minus 3 i am construit imaginea

sa geometrică a mutat cu m punctul

de coordonate 2 și minus 3 și ne

propunem să scriem acest număr

sub formă trigonometrică calculăm

mai întâi aer inel modul din z

și a egal cu radical din 2 la pătrat

plus minus 3 la pătrat egal cu

radical din 4 plus 9 13 argumentul

numărului complex z este măsura

în radiani a acestui unghi acesta

este unghiul t voi nota cu alfa

unghiul acesta a om și folosim

relația te este egal cu 2 pi minus

Alfa Deci unghiul te se obține

dacă efectuăm o rotație completă

apoi scădem acest unghi Alfa pentru

a calcula unghiul Alfa aplicăm

tangenta în triunghiul a o m tangentă

de Alfa este cateta opusă a m supra

cateta alăturată a o egal a m este

modul din minus 3 iar AO este 2

egal cu 3 pe 2 Alfa va fi egal

cu arc tangentă de 3 supra 2 nu

cunoaștem unghiul a cărui tangentă

este 3 supra 2 Așadar vom lăsa

unghiul Alfa a scris sub forma

aceasta te va fi egal cu 2 pi minus

arc tangentă de trei pe doi am

găsit raza polară și argumentul

redus Așadar să scriem formă trigonometrică

a lui z z va fi egal cu aer pe

lângă cosinus de T plus e sinus

de TE egal cu radical din 13 pe

lângă cosinus de 2 pi minus arc

tangentă de trei pe doi acesta

este unghiul t plus e sinus de

2pi minus ar tangentă de trei pe

doi aceasta este forma trigonometrică

a numărului complex z Putem să

scriem și argumentul lui z mama

avea argumentul redus adică 2pi

minus arctangenta de 3 supra 2

plus 2k unde k este număr întreg