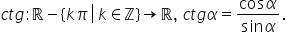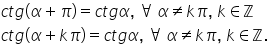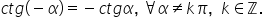Funcția cotangentă

în această lecție o să discutăm

despre funcția cotangentă și proprietățile

acesteia avem cercul trigonometric

și am construit o tangentă la cerc

aceasta intersectează cercul în

punctul A am construit de asemenea

un unghi Alfa în sens trigonometric

și am prelungit raza vectoare om

până intersectează tangenta întru

un punct pe care îl am notat cu

b abscisa punctului b este proiecția

punctului pe axa o x și am notat

abscisa cu X iar ordonata punctului

b este dată de proiecție a acestui

punct pe axa o y mai exact de lungimea

segmentului o A dar o a este raza

În cercul trigonometric prin urmare

ordonat acestui punct este egală

cu 1 observăm că tangentă la cerc

este paralelă cu Axa o x prin urmare

aceste două unghiuri sunt congruente

ele fiind unghiuri alterne interne

și acum ne uităm În triunghiul

dreptunghic a o b dreptunghic în

A și avem cotangentă de Alfa este

raportul dintre cateta alăturată

unghiului Alfa și cateta opusă

Deci ab supra o A dar lungimea

segmentului AB este egală cu X

iar lungimea segmentului AO este

1 Prin urmare avem cotangentă de

Alfa egal cu x observăm Așadar

că putem să construim o funcție

care Asociază fiecărui unghi Alfa

din orice cadran abscisa punctului

de pe tangentă iar această funcție

va fi în acest triunghi AOB putem

exprima sinusul și cosinusul unghiului

Alfa și putem observa că funcția

cotangentă se poate exprima raportul

dintre cosinus și sinus Haideți

să facem cosinus de Alfa supra

sinus de Alfa și avem cosinus de

Alfa este cateta alăturată supra

ipotenuză Deci ab supra OB iar

sinus de Alfa este cateta opusă

supra ipotenuză a o supra OB avem

AB supra OB ori o b supra a o se

simplifică și ne rămâne a b supra

a o d c egal cu cotangentă de Alfa

prin urmare funcția cotangentă

va fi definită ca raportul dintre

cosinus de Alfa și sinus de Alfa

însă funcția cotangentă nu va fi

definită pentru acele valori ale

lui Alfa pentru că are sinusul

este 0 iar sinus de Alfa este 0

când unghiul are măsura egală cu

0 grade sau 0 radiani ep 2 3 pi

și așa mai departe prin urmare

vom defini funcția cotangentă pe

r întrucât putem avea atât unghiul

pozitive cât și negative dar din

care scădem acele valori care anulează

numitorul la aceste fracții mai

exact scădem acei multiplii întregi

dep avem ca papi Și cu valori în

R Unde k este număr întreg în continuare

vom studia semnul acestei funcții

pentru unghiurile din cele patru

cadrane am văzut că valoarea funcției

cotangentă de Alfa este dată de

lungimea segmentului AB dacă segmentul

ab este situat la dreapta axa o

y atunci accesa punctului b este

pozitivă prin urmare cotangenta

este pozitivă iar dacă segmentul

ab este situat în partea stângă

axa o y a tunci Da este negativă

pentru unghiurile Alfa din primul

cadran cotangenta este pozitivă

observăm că abscisa acestui punct

este situată la dreapta axei o

e y pentru unghiurile din cadranul

2 cotangenta este negativă aici

se punctului b este negativă pentru

unghiurile din cadranul 3 Iată

am prelungit raza vectoare până

intersectează tangenta în punctul

b și observăm că funcția cotangentă

ia valori pozitive pentru unghiurile

din cadranul 3 iar pentru în grile

din cadranul 4 la fel și aici am

prelungit raza vectoare până intersectează

tangenta în punctul b iar pentru

aceste unghiuri cotangenta este

negativă în cazul în care unghiul

are măsura egală cu 0 grade sau

0 radiani atunci raza vectoare

este paralelă cu tangenta Așadar

funcția cotangentă nu are o valoare

reală pentru unghiul cu măsura

de 0 grade sau 0 radiani întrucât

nu există punct de intersecție

între raza vectoare și tangentă

putem spune că pentru unghiul de

0 Radian cotangenta are valoarea

egală cu plus infinit în cazul

în care unghiul Alfa are măsura

egală cu radiani atunci observăm

că și în această situație raza

vectoare este paralelă cu tangenta

însă orientată la stânga axa o

y prin urmare vom spune că funcția

cotangentă de pi are valoarea egală

cu minus infinit în continuare

vom studia monotonia acestei funcții

pentru unghiurile din cadranul

întâi observăm că cu cât crește

măsura unghiului Alfa a cu atât

scade lungimea segmentului AB prin

urmare funcția cotangentă este

descrescătoare chiar strict descrescătoare

pentru unghiurile din cadranul

2 funcția de asemenea este descrescătoare

pentru că cu cât crește măsura

unghiului Alfa abscisa punctului

b scade de la 0 la minus infinit

Pentru unghiurile din cadranul

al treilea funcția cotangentă este

descrescătoare cu cât crește măsura

unghiului Alfa cu atât ca de lungimea

segmentului AB iar pentru unghiurile

din cadranul al patrulea funcția

a fost tangentă este de asemenea

descrescătoare aceasta ia valori

negative de la 0 către minus infinit

în continuare vom studia paritatea

aceste funcții ca și funcția tangentă

funcția cotangentă este o funcție

impară Iată Dacă vom construi un

unghi în sens negativ am construit

aici un unghi egal în modul cu

unghiul Alfa dar orientat în sens

negativ prin urmare cotangenta

acestui unghi va fi dată de abscisă

acestui punct am prelungit raza

vectoare până intersectează tangenta

iar segmentul acesta care se formează

pe tangentă are aceeași lungime

cu segmentul ab Însă este orientat

în sens negativ prin urmare putem

spune că funcția cotangentă de

minus Alfa este egală cu minus

cotangentă de Alfa Așadar funcția

cotangentă este o funcție impară

singura funcție pară este funcția

cosinus ca și funcția tangentă

funcția cotangentă este o funcție

periodică având perioada principală

egală cu piată dacă la acest unghi

adunăm radiani atunci în Baum obține

unghiul acesta Așadar aici avem

unghiul Alfa plus pai observăm

că acestui unghi corespunde același

punct pe tangentă prin urmare abscisa

unghiului Alfa coincide cu abscisa

unghiului Alfa plus pai prin urmare

cotangentă de Alfa este egală cu

cotangentă de Alfa plus p Așadar

funcția cotangentă este o funcție

periodică având perioada principală

egală cu pi graficul acestei funcții

se va reprezenta pe un interval

de lungime a unei perioade de regula

acest interval este zero p iar

apoi se regenerează translate în

duel la stânga și la dreapta Am

de a lungul axei o x Haideți să

vedem și graficul acestei funcții

acesta este graficul funcției cotangentă

observăm că funcția este descrescătoare

pe intervalul 0 pini apoi funcția

cotangentă nu este definită în

punctele 0 p2p minus pe minus 2

pi și așa mai departe stau mai

putem spune că în aceste puncte

funcție a fost tangentă nu are

o valoare reală deoarece cotangentă

de 0 este plus infinit iar cotangentă

de pi este minus infinit de asemenea

trebuie remarcat faptul că funcția

cotangentă este o funcție periodică

iar perioada principală este egală

cu pi prin urmare este suficient

să Reprezentăm graficul acesteia

pe intervalul 0 pi și apoi să îl

translator de a lungul axei o x