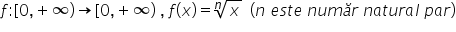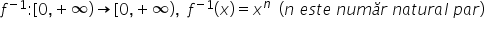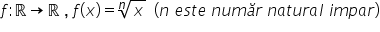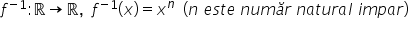Funcția radical de ordin n

în lecția trecută am discutat despre

funcția putere și am văzut reprezentarea

grafică a funcției f definită pe

r cu valori in r f de x egal cu

x la a doua această funcție nu

este bijectivă dar dacă luăm în

considerare restricția a la intervalul

0 plus infinit și cu valori în

mulțimea 0 plus infinit funcția

devine bijectivă și inversabilă

Să considerăm Așadar funcția f

definită pe intervalul 0 plus infinit

cu valori în intervalul 0 plus

infinit dată de legea f de x egal

cu x la a doua această funcție

este inversabilă iar inversa a

va fie funcția f la minus 1 definită

pe intervalul 0 plus infinit cu

valori în intervalul 0 plus infinit

exprimată prin legea f la minus

1 de x egal cu radical Linex această

funcție se numește funcția radical

de ordinul 2 trasarea graficului

aceste funcții se va face prin

puncte funcția directă x la a doua

trece prin originea reperului cartezian

și prin punctele de coordonate

1 1 și 2 4 având în vedere că funcția

inversă inversează aceste valori

putem deduce că graficul funcției

radical din x va trece prin punctele

de coordonate 1 1 și 4 2 să trasăm

în continuare graficul funcției

radical din x pentru a reprezenta

grafic funcția radical din x vom

Uni printr o linie continuă punctele

de coordonate 0 0 1 1 și 4 2 Iată

acesta este graficul funcției radical

din x monotonia funcției radical

din x Se poate stabili ținând cont

de monotonia funcției directe întotdeauna

inversă unei funcții are aceeași

monotonie cu funcția directă funcția

x la a doua era o funcție strict

crescătoare pe intervalul 0 plus

infinit și atunci și funcția radical

din x va fi strict crescătoare

pe intervalul 0 plus infinit Nu

are sens să studiem paritatea aceste

funcții întrucât domeniul de definiție

intervalul 0 plus infinit Nu este

o mulțime simetrică așa dar nu

putem calcula f de minus x putem

observa că această funcție are

doar valori pozitive iar graficul

acesteia este situat deasupra axei

o x Dacă vom reprezenta în același

reper cartezian graficele funcțiilor

x la a doua și radical din x se

poate observa că acestea sunt simetrice

față de prima bisectoare Până acum

am discutat despre funcția radical

de ordinul 2 iar în continuare

vom prezenta principalele proprietăți

ale funcției radical de ordinul

3 pornind de la funcția directă

f de x egal cu x la a treia al

cărei grafic este redat în această

imagine funcția este bijectivă

pe întreg domeniul de definiție

aer pentru că oriunde aș duce o

paralelă la axa o x aceasta intersectează

graficul funcției în act un punct

avem Așadar funcția directă f definită

pe r cu valori in R exprimată prin

legea f de x egal cu x la puterea

a treia inversă aceste funcții

va fi la minus 1 definită pe r

cu valori în aer dată prin legea

radical de ordinul 3 din x aceasta

este funcția radical de ordinul

3 trasarea graficului aceste funcții

se va face tot prin puncte obține

cont de faptul că funcția directă

x la a treia trece prin originea

reperului cartezian și prin punctele

de coordonate 1 1 3 supra 2 și

27 pe 8 respectiv minus 1 minus

unu și minus 3 supra 2 minus 27

pe 8 funcția radical de ordinul

3 din x va inversa aceste valori

și atunci graficul acesteia va

trece prin punctele de coordonate

1 127 pe 8 3 pe 2 respectiv minus

1 minus unu și minus 27 pe 8 minus

3 pe 2 să vedem în continuare în

graficul funcției radical de ordinul

3 din x Demonii printro linie continuă

punctele de coordonate 0 0 unu

unu și 27 pe 8 3 pe 2 27 supra

8 este aproximativ 3 iar 3 supra

2 este 1 graficul se continuă prin

punctele de coordonate minus 1

minus 1 și minus 27 pe 8 minus

3 pe 2 Iată acesta este graficul

funcției radical de ordinul 3 din

x funcția păstrează monotonia funcției

directe astfel funcția este strict

crescătoare pe r se poate verifica

că funcția este impară pentru că

f de minus x este egal cu minus

f de x iar referitor la semnul

funcției observăm că funcția are

valori pozitive pe intervalul 0

plus infinit graficul fiind situat

deasupra axei o x și valori negative

pe intervalul minus infinit 0 pentru

că în această zonă graficul este

situat sub axa o x dacă Reprezentăm

în același reper cartezian graficele

funcțiilor x la a treia și radical

de ordinul 3 din x se poate observa

că acestea sunt simetrice față

de prima bisectoare în continuare

vom defini funcția radical de ordinul

n pentru n par respectiv N impar

Dacă n este număr natural par Considerăm

funcția f definită pe intervalul

0 plus infinit cu valori în intervalul

0 plus infinit exprimată prin legea

f de x egal cu radical de ordinul

n din x aceasta se va numi funcția

radical de ordin par Ea este o

funcție inversabilă iar invers

a acesteia este funcția f la minus

1 definită pe intervalul 0 plus

infinit cu valori în 0 plus infinit

f de x egal cu x la puterea n este

greșit să spunem că inversă a funcției

radical de ordinul par este funcția

putere x la n pentru că funcția

putere era definită pe r cu valori

in r iar Aici avem alt domeniu

respectiv codomeniu în cazul în

care an este impar Considerăm funcția

f definită pe r cu valori în aer

x egal cu radical de ordinul n

din x aceasta este funcția radical

de ordin impar iar inversa ei este

funcția putere f la minus 1 va

fi definită pe r cu valori în aer

taf la minus 1 de x este egal cu

x la puterea n este important să

reținem că la adică lydiard din

par există doar din valori pozitive

în schimb radicalul de ordin impar

se poate Extrage din orice număr

aici nu avem nici o restricție

să rezolvăm în continuare următorul

exercițiu Stabiliți domeniul de

definiție pentru funcțiile la punctul

a avem e f de x egal cu radical

de ordinul 3 din 2 plus x având

în vedere că avem un radical de

ordin impar nu trebuie pusă nicio

condiție asupra valorii de sub

radical Așadar în această situație

domeniul de definiție este mulțimea

numerelor reale la punctul B avem

funcția f de x egal cu radical

din 1 minus 7x aici avem un radical

de ordinul 2 iar radicali de ordin

par există doar din valori pozitive

vom pune condiția ca 1 minus 7x

să fie mai mare sau egal cu 0 de

aici vom obține 1 mai mare sau

egal decât 7 x x mai mic sau egal

decât 1 supra 7 definiție va fi

intervalul minus infinit 1 supra

7