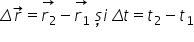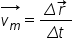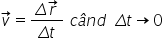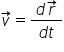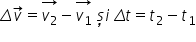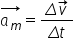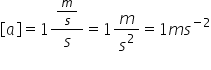Operaţii cu vectori. Viteza şi acceleraţia.

În ce dată doua lecție de mecanică

newtoniană vom vorbi despre operații

cu vectori și apoi despre viteză

și accelerația în lecția trecută

am introdus noțiunea de vectori

și proprietățile ei vom vorbi acum

despre adunarea vectorilor și scăderea

lor să luăm doi vectori a și b

și să construim suma lor esti diferența

lor tei la început folosind metoda

paralelogramului primul pas este

propunerea celor doi vectori a

și b coadă la coadă adică pornind

din același punct și formăm paralelogramul

care are laturile egale cu a și

b atunci vectorul sumă S va fi

diagonala paralelogramului ce pleacă

din același punct ca și vectorii

originali pentru a forma vectorul

diferență observăm că diferența

a doi vectori a minus b în cazul

ăsta Acesta este de fapt același

lucru ca suma lor în sensul că

a minus b este egal cu a plus minus

Deci formăm vectorul minus pe care

este egal în magnitudine cu b are

aceeași direcție adică dreaptă

de suport dar sens contrar deci

a minus b va fi diagonala paralelogramului

cu o latură egală cu minus b observăm

că În paralelogramul originar vectorul

diferență de este diagonala mică

a paralelogramului există două

metode alternative foarte foarte

similare cu metoda paralelogramului

la pot fi folosite în loc și anume

pentru adunare putem folosi metoda

numită cap coadă în care cei doi

vectori de adunat a și b sunt puși

coadă la cap adică alegem latura

opusă pentru beci această latură

este tot vectorul b dar punem vectorul

b cu coada la capul vectorului

și atunci suma s Completează triunghiul

Deci metoda cap coadă presupune

punerea celor doi vectori cu coada

celui de al doilea la capul primului

lector deci a și b sunt acești

doi vectori și atunci vectorul

sumă va completa triunghiul format

de a și b pentru diferență putem

folosi metoda coadă coadă care

din nou se vede în metoda paralelogramului

deci punem vectorii de scăzut a

și b coadă la coadă Și atunci vectorul

diferență va completa triunghiul

Deci dacă luăm vectorul A punem

vectorul b cu coada la Coada vectorului

a b c avem a și b m și atunci vectorul

diferență de fac Completați unghiul

vârful vectorului de corespunde

cu vârful primului Factor din diferență

în cazul acesta vectorul a să dăm

un exemplu intuitiv al acestor

operații cu Vector Să considerăm

că doriți să ajungeți în Frankfurt

plecând din București o metodă

de a face acest lucru este de a

lua un zbor Lufthansa să notăm

această metodă de zbor cu unul

dar în același timp puteți ajunge

în Frankfurt London zbor Tarom

zboruri Tarom afaceri scol în Cluj

Deci veți ajunge în Frankfurt unui

rând de la București la Cluj notăm

acest Vector cu 2 și apoi din Cluj

la Frankfurt pe care îl notăm cu

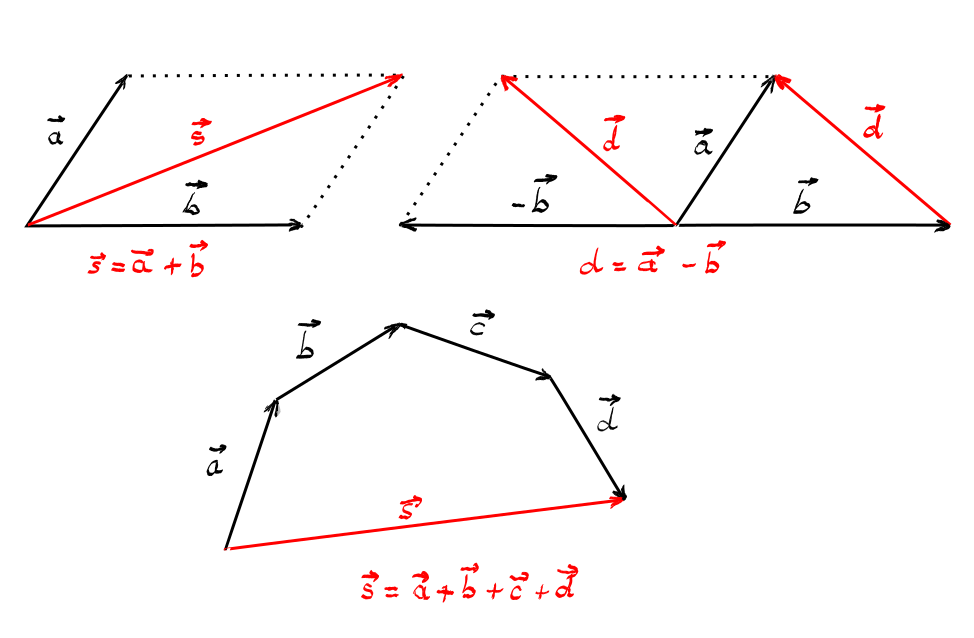
3 se poate observa imediat că suma

vectorilor doi și 3 este egală

cu vectorul 1 aceasta deoarece

cei doi vectori sunt coadă la cap

iar vectorul 1 Completează triunghiul

interpretare intuitivă fiindcă

cei trei vectori dau o dau două

metode alternative de ajungi în

același punct plecând din același

punct Deci plecăm din București

și ajungem în Frankfurt prin două

pe două drumuri iar suma vectorilor

de pe drumul la doilea va da același

rezultat ca vectorul de pe primul

drum la fel foarte ușor se poate

vedea că vectorul 3 este egal cu

diferența dintre vectorul 1 și

vectorul 2 și interpretarea evidentă

fiindcă vectorul diferență ne arată

cu cât zboară cei din Cluj mai

puțin decât cei care zboară din

București care deși au două alternativele

ajunge în Frankfurt Voi mai mult

în operațiile cu vectori direcția

și sensul sunt la fel de importante

ca și magnitudinea pentru a arăta

acest lucru important pe care îl

vom întâlni de multe ori Să considerăm

doi vectori cu aceeași magnitudine

să zicem 5:00 o pereche de vectori

cu magnitudinea 5 și vom face diferite

operații cu ei în primul rând Să

considerăm acest Vector ca fiind

coliniari atunci suma celor doi

vectori va da deci cinci plus cinci

va da 10 în cazul în care ei sunt

luați cu același sens dar de ce

nu acest caz 5 plus 5 de zeci dar

putem să luăm vectorii ca având

sensuri opuse deci 5 plus 5 din

nou dar sensurile celor două vectori

celor doi vectori sunt contrare

în acest caz suma va da 0 deci

5 plus 5 în acest caz este egal

cu zero putem să luăm acești doi

vectori ca fiind ortogonali pentru

a face suma lor folosind metoda

cap coadă deci punem cel de al

doilea factor cu coada la capul

primului Vector Și luăm un unghi

de 90 de grade între ei aceasta

înseamnă că sunt ortogonali Deci

avem cei doi vectori și suma lor

este ipotenuza Deci vectorul sumă

este acesta și nu poate fi calculat

cu teorema Pitagora care spune

că ipotenuza la pătrat Pitagora

care spune că ipotenuza la pătrat

deces pătrat este egală cu suma

catetelor la pătrat Deci cinci

pătrat plus 5 pe la pătrat rezultă

că în acest caz suma celor doi

vectori 5 plus 5 va da 7 7 Sectorială

deci 5 plus 5 sumă vectorială poate

da 7 plus în 7 7 la fel putem vedea

pentru scădere în cazul vectorilor

coliniari că diferența de rezultate

foarte diferite în funcție de orientare

și sensul direcția și sensul celor

doi vectori de cinci minus cinci

vectori au același sens de mod

Evident 0 deci 5 minus 5 este egal

cu 0 dar la fel de bine dacă cei

doi vectori au orientări contrare

sensuri contrare aceeași direcție

dar sens contrar Deci cel de al

doilea factor are sens contrar

atunci obținem o diferență egală

cu 10 Deci 5-a minus 5 poate fi

egal cu 10 și pentru vectori ortogonali

punem cei doi vectori descăzut

coadă la coadă vrei amintesc scăderea

se face prin metoda coadă la coadă

un unghi de 90 de grade doi vectori

cu magnitudinea 5 și vectorul diferență

este ipotenuza și aplică metoda

Pitagora obținem la fel că 5 minus

5 pentru vectorul ortogonali de

7 7 vector Deci folosind doi vectori

cu aceeași magnitudine sau modul

și anume 5 putem obține pentru

adunarea și scăderea lor rezultate

foarte diferite în funcție de Direcția

și sensul celor doi vectori să

introducem viteza unui mobil aflat

pe o traiectorie rectilinie dea

lungul coordonatei x Deci ne aflam

pe axa de coordonate o x aleasă

de a lungul traiectoriei dacă acest

mobil trece prin punctul a aflat

în poziția X1 la momentul T1 și

prin punctul B aflată în poziția

X2 la momentul T2 putem defini

viteza medie a mobilului pe segmentul

ab al traiectoriei ca fiind Delta

x adică x 2 minus x 1 împărțit

la Delta t Adică te 2 minute 1

să observăm că dacă luăm mai multe

puncte de a lungul acestei traiectorie

notate aici cu c d și e de exemplu

viteza medie pe veri segmente ale

traiectoriei este în general diferită

pentru că de obicei îmi și care

este neuniformă adică mai înceată

sau mai rapidă pe Vali segmentele

ale tractor in Aceasta este o problemă

dacă dorim să definim viteza momentană

la moment dat A deci dacă considerăm

un moment dat te da lungul traiectorii

și vrem să definim viteza exact

în acest punct Nu putem deoarece

viteza medie este definită pentru

interval în jurul momentului te

interval în care în mod uzual viteza

variază nu avem o singură valoare

pentru acest vede la momentul te

Deci pentru a rezolva această problemă

trebuie să considerăm punctele

sau momentele T1 și T2 ce încadrează

momentul t m astfel încât Delta

t să fie foarte mică acest interval

temporar cetine de către 0 Pentru

că atunci nu mai avem de a face

cu ou variația vitezei în acest

interval valoarea vitezei E unică

Deci definită și putem introduce

viteza momentană la momentul t

definită ca și viteza medie dar

cu specificarea foarte importantă

că Delta te tin de către 0 pentru

a introduce viteza în cazul mai

general 3 Dimensional facem extensiei

simplă vectorul viteză medie pe

același sector a b Dar al unei

traiectorii tridimensionale în

acest caz va fi definit ca Delta

R pe Delta t adică r 2 minus seru

nu diferența dintre vectorii poziție

la cele două momente T2 și te 1

împărțit la diferența dintre doi

și te 1 bineînțeles această diferență

este o diferență vectorială la

fel se introduce și vectorul viteza

momentană ca fiind Delta R împărțit

la Delta t dar cu Delta t tinde

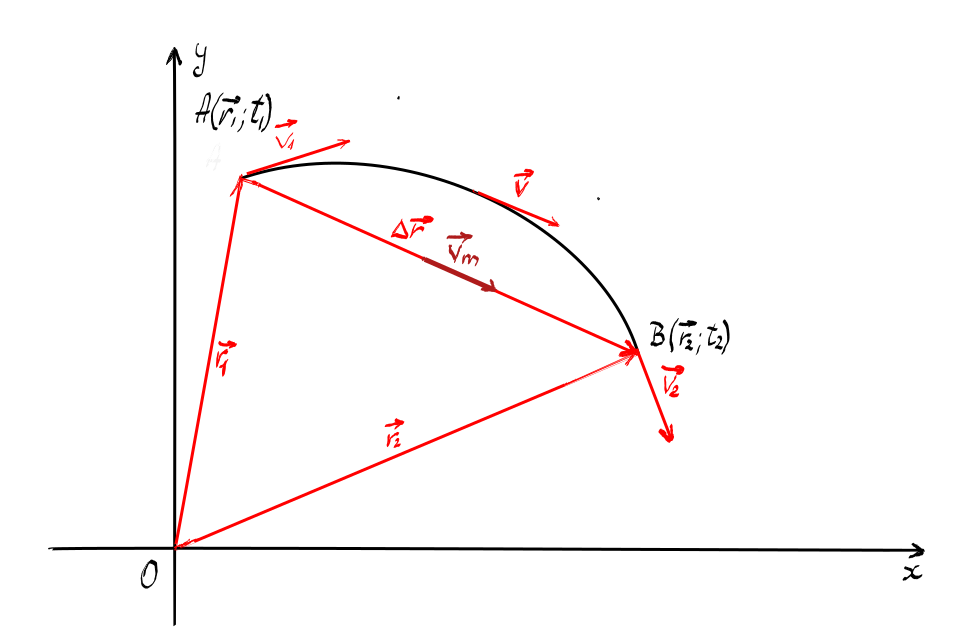
la 0 Să considerăm un alt caz cel

al traiectoriei curbilinii Deci

pentru traiectoria curbilinie în

particular în acest desen consideram

o traiectorie circulară vectorul

poziție ia va descrie verii poziții

pe acest cerc corespunzând verilor

momente d1 și d2 în acest caz dacă

Delta t tinde către 0 Delta t care

este prin definiție te 2 minus

de 1 minus t 1 tinde către 0 atunci

cele cei doi vectori aer 1 și r

2 Se apropie foarte mult pentru

că distanța dintre cele două poziții

scade și atunci vectorul aer din

mijlocul acestui segment de cerc

va fi perpendicular pe Delta aer

Da deci pentru Delta te tin de

către 0 1 și r 2 Se apropie foarte

mult unul de celălalt devenind

un Vector R care devine perpendicular

pe e dar viteza la momentul t este

definită ca Delta Air PDL tot A

deci în concluzie viteza momentană

la momentul t m este perpendiculară

pe vectorul poziție la acel moment

te În consecință dacă acesta este

vectorul aer la momentul t Viteza

va fi tangentă viteza la momentul

t va fi tangentă la cerc în în

raza descrisă de rdt magnitudinea

vitezei momentane vedete este definită

tot prin de el tire împărțită la

del tate mici magnitudinea vectorului

este magnitudinea aceste diferențe

pentru accelerație de formulele

directe fără a mai explicat foarte

mult pentru că ideea este aceeași

accelerația pe un segment AB de

dreaptă este viteza de variația

vitezei Deci Delta V împărțit la

Delta t pe acel segment a b accelerația

momentană se definește identica

Viteza momentană e viteza de variația

vitezei Deci Delta veni pe Delta

t dar cu un Delta t tinzând către

0 iar extensia încă pentru cazul

3 dimensionali Deci pentru Vector

este imediată a m Vita accelerația

medie vectorială pe segmentul a

b este definită ca Delta V Vector

împărțită la deltat A deci diferența

celor doi vectori viteză V1 minus

seria 2 împărțit la Delta t iar

accelerația momentană este definită

ca Delta V împărțită la Delta t

cu Delta t tinzând către 0
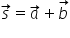
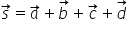
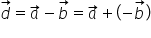
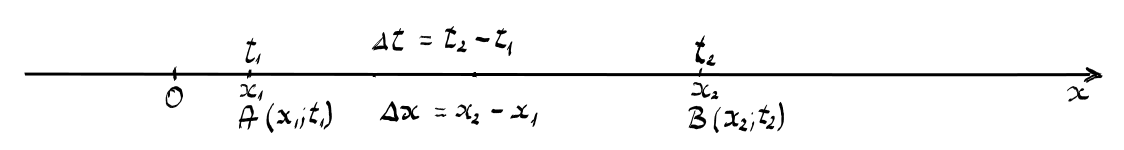
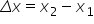
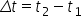
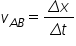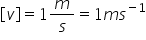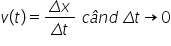
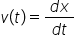
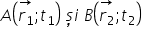