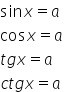Rezultate pentru tag: f
Proiecții ortogonale pe un plan
Proiecția unui punct pe un plan. Proiecția unui segment pe un plan. Lungimea proiecției unui segment pe un plan. Proiecția unei drepte pe un plan.
Teorema celor trei perpendiculare
Distanța de la un punct la o dreaptă în spațiu. Teorema celor trei perpendiculare. Enunțul și demonstrația teoremei celor trei perpendiculare.
Reciprocele teoremei celor trei perpendiculare
Enunțarea reciprocelor teoremei celor trei perpendiculare.
Unghiul a două plane
Unghi diedru. Unghi plan al unui diedru. Determinarea măsurii unghiului format de două plane
Prisma triunghiulară regulată
Aria prismei și volumul prismei. Deducerea formulelor de calcul pentru arie prismă triunghiulară și volum prismă triunghiulară regulată. Aria laterală a prismei triunghiulare regulate. Aria totală a prismei triunghiulare regulate. Volumul unei prisme triunghiulare regulate.
Propagarea luminii. Reflexia si refracţia.
Propagarea luminii în medii omogene: constanţa vitezei şi conceptul de rază de lumină. Legile reflexiei şi refracţiei. Reflexia totală: definiţie, aplicaţii.
Prisma. Oglinzi plane şi sferice.
Prisma optică. Formarea imaginilor. Oglinda plană. Oglinzi sferice: proprietăţi, construcţia imaginilor.
Aproximaţiile lentilei. Lentila convergentă.
Aproximaţiile lentilei: lentila subţire, stigmatismul. Lentila convergentă: proprietăţi, construcţia imaginilor.
Lentile divergente. Convergenţa lentilelor.
Lentile divergente: proprietăţi, construcţia imaginilor. Convergenţa lentilelor: definiţie, ecuaţie.
Formulele lentilelor: Newton şi Descartes.
Explicarea convenţiei de semn pentru lentile. Deducerea formulelor Newton şi Descartes pentru imagini în lentile.
Calculul lentilelor. Sisteme de lentile.
Folosim formula Descartes pentru a calcula proprietăţile imaginii formate într-o lentilă. Prezentăm sistemele centrate şi acolate de lentile.
Microscopul. Ochiul uman.
Exemple de instrumente optice cu sisteme centrate de lentile: microscopul (parametri, exemple) şi ochiul uman (componente, acomodarea).
Imagini şi obiecte virtuale.
O discuţie detaliată asupra conceptelor de obiect virtual şi imagine virtuală: semnificaţie, proprietăţi.
Dispersia luminii.
Definiţia dispersiei. Descompunerea luminii albe în spectrul de radiaţii vizibile. Dispersia în prisma optică. Dispersia normală şi anomală.
Interferenţa luminii. Dispozitivul Young.
Interferenţa staţionară: surse coerente; intensitate constantă; franje luminoase şi întunecate. Dispozitivul Young.
Interferometrele Lloyd şi Fresnel.
Interferometre nelocalizate: oglinda Lloyd, oglinzile Fresnel şi biprisma Fresnel.
Lama cu feţe plan paralele.
Aplicaţii ale interferenţei nelocalizate. Lama cu feţe plan paralele: franjele de egală înclinare. Stratul antireflex.
Pana optică.
Interferometre cu interferenţă localizată. Pana optică: franje de egală grosime. Inelele Newton.
Difracţia luminii.
Definiţie, exemple. Franje de difracţie printr-o fantă. Reţele de difracţie.
Polarizarea luminii.
Stările de polarizare a luminii. Polarizarea prin reflexie - legea Brewster. Polarizarea prin transmisie - polarizorii. Legea Malus. Birefringenţa.
Noțiuni introductive
Materia, substanțe, molecule, atomi, ioni. Particulele subatomice: electroni, protoni, neutroni. Unitatea atomică de masă (u.a.m.) și sarcina electrică. Numărul atomic Z, numărul de masă A, numărul de neutroni N.
Masă atomică. Izotopi. Mol de atomi
Masa atomică relativă medie. Compoziția procentuală a izotopilor în natură. Numărul lui Avogadro.
Noţiuni de cinematică.
Introducem noţiunile şi mărimile de bază ale cinematicii. Discutăm ecuaţia de mişcare. Prezentăm definiţia şi proprietăţile vectorilor.
Viteza şi acceleraţia.
Metode de adunare şi scadere a vectorilor. Viteza medie şi viteza momentană. Acceleraţia medie şi acceleraţia momentană.
Mişcarea rectilinie uniform variată.
Definiţie, legea vitezei, ecuaţia mişcării, relaţia Galilei.
Mişcarea circulară uniformă.
Definiţie, ecuaţia de mişcare, mărimi caracteristice, acceleraţia centripetă.
Noţiuni de dinamică. Principiile mecanicii.
Inerţia şi masa, principiul I (al inerţiei), forţa, principiul II (fundamental.)
Acţiunea şi reacţiunea. Problemă de dinamică.
Principiul III, al acţiunii şi reacţiunii. Exemplu de problemă dinamică rezolvată.
Elasticitatea. Legea Hooke.
Elasticitatea. Forţa elastică. Legea Hook. Efortul unitar.
Forţa de frecare. Corpul pe plan înclinat.
Frecarea. Forţa de frecare. Aplicaţiile frecării. Corpul pe plan înclinat.
Legea atracţiei gravitaţionale.
Legea atracţiei gravitaţionale universale. Câmpul gravitaţional terestru.
Echilibrul de translaţie.
Echilibrul de translaţie sub acţiunea a două sau mai multe forţe. Echilibrul punctului material supus la legături.
Momentul forţei. Cuplul de forţe.
Efectul forţelor la rotaţia unui solid rigid. Momentul forţei şi cuplul de forţe. Convenţii de semn.
Echilibrul de rotaţie.
Legea echilibrului de rotaţie. Exemple. Stabilitatea echilibrului.
Lucrul mecanic.
Definiţie. Interpretare geometrică. Forţe conservative. Lucrul mecanic al forţelor elastică şi de greutate.
Puterea şi randamentul.
Definiţia puterii. Randamentul unei maşini. Randamentul planului înclinat.
Energia cinetică şi energia potenţială.
Energia cinetică. Teorema variaţiei energiei cinetice. Energia potenţială gravitaţională şi elastică.
Legea conservării energiei mecanice.
Energia mecanică. Legea conservării energiei mecanice. Exemple de aplicare în cazuri concrete.
Legea conservării impulsului.
Impulsul forţei. Impulsul punctului material. Legea conservării impulsului. Exemple.
Mişcarea oscilatorie armonică.
Mărimi caracteristice ale mişcării oscilatorii. Mişcarea oscilatorie armonică. Pendulul elastic.
Proprietăţile mişcării oscilatorii armonice.
Defazaje, reprezentarea fazorială, conservarea energiei. Pendulul gravitaţional.
Oscilaţii amortizate. Compunerea oscilaţiilor paralele.
Forţa rezistivă şi amortizarea oscilaţiilor. Compunerea a două oscilaţii paralele.
Compunerea oscilaţiilor perpendiculare.
Discuţia fenomenului de bătăi. Compunerea a două oscilaţii perpendiculare.
Oscilaţii forţate. Rezonanţa.
Oscilaţii cuplate şi oscilaţii forţate. Fenomenul de rezonanţă a oscilaţiilor cuplate.
Modelul undei plane.
Unde mecanice: definiţie, mărimi caracteristice. Unde longitudinale şi transversale. Modelul undei plane.
Ecuaţia undei plane.
Deducerea ecuaţiei undei plane. Proprietăţile undei plane: periodicitatea, intensitatea.
Principiul Huygens. Reflexia undelor.
Principiul Huygens - propagarea frontului de undă. Reflexia undelor mecanice.
Refracţia undelor.
Refracţia undelor mecanice. Seismologia - undele mecanice terestre.
Interferenţa undelor.
Interferenţa undelor mecanice. Unde staţionare. Formarea ventrelor si nodurilor.
Interferenţa prin reflexie.
Interferenţa prin reflexie. Unde mecanice staţionare în corzi şi tuburi.
Instrumente muzicale. Acustica.
Unde staţionare în instrumente muzicale şi organe umane. Acustica.
Structura substanţei.
Structura substanţei. Ipoteza atomică. Numarul lui Avogadro. Molul.
Noţiuni de termodinamică.
Sistem termodinamic. Stări şi parametri de stare. Procese şi parametri de proces. Echilibru termodinamic.
Echilibrul termic. Temperatura.
Echilibrul termic. Temperatura. Scări de temperatura. Termometre.
Procese izobare. Procese izocore.
Procese izobare: legea Gay-Lussac. Procese izocore: legea Charles. Temperatura zero absolut.
Procese izoterme. Ecuaţia generală a gazelor.
Procese izoterme: legea Boyle-Mariotte. Ecuaţia generală a gazelor (Clapeyron-Mendeleev).
Teoria cinetico-moleculara: fundamente.
Principiul echipartiţiei energiei pe grade de libertate. Formula fundamentală a teoriei cinetico-moleculare.
Teoria cinetico-moleculara: aplicaţii.
Deducerea legii Dalton. Extinderea modelului gazului ideal la substanţe reale. Clasificarea stărilor de agregare.
Calorimetrie I.
Lucrul mecanic: definiţie, ecuaţii pentru varii procese. Căldura. Coeficienţi calorici: definţii, tipuri.
Calorimetrie II.
Calorimetrul şi utilizarea lui. Ecuaţia calorimetrică. Energia internă.
Principiul I. Maşina termică.
Principiul I al termodinamicii. Maşina termică. Perpetuum mobile de speţa I şi II. Relaţia Mayer.
Motoare termice.
Randamentul maşinii termice. Motoarele termice Otto şi Diesel.
Ciclul Carnot.
Ciclul Carnot. Teorema Carnot: randament maxim. Motorul cu reacţie.
Entropia. Principiul II.
Entropia: definiţie, interpretare. Procese reversibile şi ireversibile. Principiul II al termodinamicii.
Transformări de stări de agregare.
Stări de agregare: definiţie, faze, transfromări. Vaporizarea, evaporarea, fierberea. Căldura latentă.
Lichefierea, topirea. Diagrama de fază.
Izotermele Andrews ale gazului real. Lichefierea. Topirea şi solidificarea. Diagramele de fază. Punctul triplu.
Legea Coulomb. Câmpul electric.
Sarcina electrică. Legea Coulomb a interacţiunii electrostatice. Câmpul electric, linii de câmp.
Mărimile câmpului electric. Capacitatea electrică.
Potenţialul electric, tensiunea electrică, lucrul mecanic electric. Energia potenţială electrostatică. Capacitatea electrică.
Condensatorul electric.
Condensatorul electric. Condensatorul plan. Gruparea în serie şi paralel a condensatoarelor.
Tensiunea şi intensitatea.
Mecanismul de generare a curentului electric. Tensiunea electromotoare. Intensitatea curentului electric.
Rezistenţa. Legea Ohm.
Rezistenţa şi rezistivitatea electrica. Supraconductibilitatea. Legea Ohm pentru o porţiune şi pentru întregul circuit.
Legile Kirchhoff.
Reţele electrice. Legile Kirchhoff. Convenţii de semn. Exemplu de aplicare.
Gruparea rezistoarelor.
Grupările în serie şi paralel ale rezistoarelor. Grupările în stea şi triunghi ale rezistoarelor.
Gruparea generatoarelor.
Gruparea în serie şi paralel a generatoarelor. Metoda superpoziţiei de calcul a reţelelor.
Măsurători electrice.
Şuntul ampermetrului. Rezistenţa adiţională a voltmetrului. Montaje aval şi amonte. Puntea Wheastone.
Legea Joule. Electroliza.
Energia electrică – legea Joule. Puterea electrică. Randamentul electric. Efectul chimic - electroliza.
Câmpul magnetic. Forţa electromagnetică.
Câmpul magnetic. Produsele scalare şi vectoriale ale vectorilor. Forţa electromagnetică.
Inducţia magnetică. Forţa electrodinamică.
Inducţia magnetică: conductorii rectiliniu şi circular, solenoidul, bobina. Forţa electrodinamică.
Inducţia electromagnetică.
Inducţia electromagnetică. Fluxul câmpului magnetic. Regula Lenz. Exemplu.
Legea Faraday.
Legea Faraday. Tensiunea electromotoare. Autoinducţia. Inductanţa: definiţie, solenoidul.
Generarea tensiunii alternative.
Energia câmpului magnetic. Exemplu: bobina. Generarea tensiunii electrice alternative. Aplicaţii.
Mărimile curentului alternativ.
Valorile momentane şi valorile efective ale mărimilor curentului alternativ: fluxul, tensiunea, intensitatea.
Reprezentarea fazoriala.
Reprezentarea fazorială a curentului alternativ. Reprezentarea fazorială polară a curentului alternativ.
Proprietăţile funcţiilor sinusoidale.
Proprietăţile funcţiilor sinusoidale: suma şi viteza de variaţie momentană.
Elemente de circuit: R, L, C.
Elemente de circuit în curent alternativ: rezistorul, bobina, condensatorul.
Circuitele RLC serie şi paralel.
Legea Ohm pentru circuite RLC serie şi paralel. Impedanţa. Construcţia diagramelor fazoriale.
Rezonanţa circuitelor RLC.
Frecvenţa de rezonanţă. Factorul de calitate. Comportarea circuitelor serie şi paralel. Interpretarea energetică.
Gruparea bobinelor. Circuit RLC mixt.
Gruparea serie şi paralel a bobinelor în curent alternativ. Rezonanţa circuitului RLC mixt.
Puterea în curent alternativ.
Puterea momentană şi puterea medie. Interpretarea geometrică. Triunghiul puterilor: puterile activă, reactivă şi aparentă.
Transformatorul. Alternatorul.
Transformatorul: raportul de transformare, randamentul. Maşini de curent alternativ. Alternatorul.
Oscilaţii electromagnetice.
Circuitul oscilant RLC. Oscilaţii electromagnetice libere, amortizate, forţate. Interpretarea energetică.
Oscilaţii electromagnetice şi oscilaţii mecanice.
O comparatie exhaustivă între oscilaţiile electromagnetice şi oscilaţiile mecanice.
Unda electromagnetică.
Principiile Maxwell ale teoriei câmpului electromagnetic. Proprietăţile undei electromagnetice: viteza de propagare, ortogonalitatea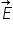 ,
, 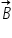 şi
şi 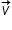 .
.
Circuitul oscilant deschis. Antene.
Circuitul oscilant deschis. Antene dipol de emisie şi recepţie. Clasificarea undelor electromagnetice.
Operaţii cu mulţimi
Operaţii cu mulţimi. Reuniunea mulțimilor. Intersecţia mulțimilor. Diferenţa mulțimilor.
Determinism predictibil. Spaţiul fazelor.
Determinismul predictibil al sistemelor clasice. Spaţiul fazelor. Atractori. Sensibilitatea la condiţiile iniţiale.
Teoria haosului. Geometrie fractală.
Determinismul impredictibil al sistemelor haotice. Atractori stranii. Geometrie fractală. Fractalul Koch.
Transformările Galilei. Relativitatea clasică.
Spaţiul şi timpul în fizica clasică. Transformările Galilei. Principiul relativităţii clasice. Electromagnetismul - o excepţie.
Experimentul Michelson.
Modelul eterului universal pentru unde electromagnetice. Experimentul Michelson: eşecul modelului eteric şi constanţa vitezei luminii în vid.
Principiile Einstein. Transformările Lorentz.
Principiile Einstein ale relativităţii restrânse. Spaţiu-timpul în fizica relativistă. Transformările Lorentz. Relativitatea simultaneităţii.
Cinematica relativistă.
Sistemul de referinţă propriu. Contracţia lungimilor. Dilatarea duratelor.
Compunerea vitezelor.
Legea compunerii vitezelor. Exemple de cinematică relativistă.
Dinamica relativistă. Ecuaţia Einstein.
Dinamica relativistă: masa, impusul şi forţa în fizica relativistă. Ecuaţia Einstein: relaţia masă-energie.
Efectul fotoelectric extern.
Dispozitiv experimental. Legile efectului fotoelectric extern. Eşecul modelului ondulatoriu de a explica efectul.
Ipotezele Planck şi Einstein.
Ipoteza Planck: cuantele de energie. Ipoteza Einstein: fotonul. Explicarea efectului fotoelectric cu formula Einstein şi modelul corpuscular.
Efectul Compton.
Dispozitivul experimental. Calculul variaţiei lungimii de undă. Eşecul modelului ondulatoriu şi succesul modelului corpuscular.
Ipoteza de Broglie. Difracţia electronilor.
Dualismul unda-corpuscul: ipoteza de Broglie. Relaţia de Broglie. Difracţia electronilor: legea Bragg.
Microscopul electronic.
Microscopul electronic: rezoluţia spaţială, funcţionare. Discuţie despre dualismul unda-corpuscul.
Relaţia de incertitudine Heisenberg.
Relatia de incertitudine Heisenberg pentru poziţie-impuls şi pentru timp-energie. Consecinţe. Exemple.
Spectre atomice.
Spectre atomice de emisie şi absorbţie: definiţii, proprietăţi. Legea seriilor spectrale ale hidrogenului. Analiza spectrală.
Experimentul Rutherford.
Dispozitiv experimental, rezultate, concluzii. Modelul planetar al atomului.
Experimentul Franck-Hertz.
Dispozitiv experimental, rezultate, concluzii. Cuantificarea energiei atomice.
Postulatele Bohr.
Postulatele Bohr ca şi consecinţe ale experimentelor Rutherford şi Franck-Hertz.
Modelul atomic Bohr I.
Modelul atomic Bohr: condiţia de cuantificare, condiţia de echilibru. Cuantificarea razelor orbitelor.
Modelul atomic Bohr II.
Cuantificarea energiei. Numărul cuantic principal. Cuantificarea vitezei. Cuantificarea vitezei de rotaţie.
Nivelele energetice ale atomului de hidrogen.
Nivelele energetice Bohr ale atomului de hidrogen. Tranziţiile atomului de hidrogen. Energia de ionizare.
Interpretarea spectrelor hidrogenului.
Interpretarea legii seriilor spectrale ale atomului de hidrogen prin modelul Bohr. Calculul constantei Rydberg.
Modelul păturilor electronice.
Modelul păturilor electronice pentru atomi cu mai mulţi electroni (Z>1). Numerele cuantice (n,l,m,mS).
Principiul de excluziune Pauli.
Principiul de excluziune Pauli. Pături (straturi) şi substraturi electronice.
Aplicaţii: radiaţiile X.
Radiaţiile X de frânare şi caracteristice: producere şi proprietăţi. Interacţiunea cu substanţa. Aplicaţii.
Aplicaţii: laseri.
LASERi: emisia stimulată, inversia de populaţie. Tehnologii de construcţie, proprietăţi, aplicaţii.
Structura învelișului electronic
Electroni. Înveliş electronic - straturi electronice, substraturi electronice, orbitali. Spin electronic.
Configurația electronică a elementelor din primele 3 perioade (Z 1-18)
Straturi electronice, substraturi electronice, orbitali. Spin electronic. Configurația electronică. Reguli de ocupare cu electroni a straturilor şi substraturilor. Principiul lui Pauli. Regula lui Hund.
Semiconductori intrinseci şi extrinseci.
Legături covalente. Semiconductori intrinseci. Semiconductori extrinseci P şi N - doparea cu impurităţi.
Configurația electronică a elementelor din perioada a 4-a
Straturi electronice, substraturi electronice, orbitali, spin electronic. Configurația electronică a elementelor din perioada a patra. Diferenţa dintre configuraţia electronică şi ordinea de ocupare cu electroni. Principiul lui Pauli. Regula lui Hund.
Tabelul periodic – grupe şi perioade
Tabelul periodic. Grupe, perioade. Legea periodicității. Grupe principale, Grupe secundare. Electron distinctiv. Metale alcaline. Metale alcalino-pământoase. Halogeni.
Poziţia elementelor în tabelul periodic şi proprietăţile periodice
Tabelul periodic. Poziţia elementelor în tabelul periodic. Proprietăţile periodice. Raza atomică, volumul atomic. Ion, cation, anion.
Dioda semiconductoare.
Dioda semiconductoare. Joncţiunea PN. Polarizarea directă şi inversă a diodei. Străpungerea joncţiunii.
Aplicaţii ale diodei. Tranzistorul.
Aplicaţii ale diodei: dioda varicap, redresarea curentului alternativ. Tranzistorul cu efect de câmp.
Forma nucleului. Forţa nucleară.
Compoziţia, forma şi densitatea nucleului. Forţa nucleară. Defectul de masă.
Modele nucleare de structură.
Modele nucleare de structură: modelul picătură de lichid şi modelul în pături.
Variaţia energiei de ionizare
Ion, cation, anion. Proprietăți periodice. Energie de ionizare - definiție, variație în tabelul periodic.
Energia de legătură. Stabilitatea nucleară.
Energia de legătură. Energia de legătură pe nucleon. Platoul de stabilitate. Procese de creştere a stabilităţii.
Variaţia proprietăţilor periodice chimice
Proprietățile periodice chimice. Electronegativitate, caracter metalic, caracter nemetalic, valență. Scara electronegativităţii. Elemente electronegative şi elemente electropozitive. Proprietăţile fizice ale metalelor şi nemetalelor. Caracterul bazic şi caracterul acid al oxizilor metalici.
Legi de conservare în reacţii nucleare.
Reacţii nucleare. Legi de conservare. Dezintegrarea nucleară.
Legătura ionică. Compuşii ionici.
Regula octetului. Legături chimice. Cedare şi primire de electroni. Punere în comun de electroni. Compuşi ionici. Ioni pozitivi – cationi. Ioni negativi – anioni. Simboluri Lewis. Substanţe cristaline. Proprietăţile compuşilor ionici.
Radiaţii nucleare. Legea dezintegrării radioactive.
Radiaţii nucleare α, β şi γ. Legea dezintegrării radioactive. Activitatea substanţelor.
Interacţia cu substanţa. Fisiunea nucleară.
Interacţia radiaţiilor α, β şi γ cu substanţa. Dozimetrie. Fisiunea nucleară şi produsele ei.
Legătura covalentă şi compuşii moleculari
Legături covalente. Compuşi moleculari. Legături covalente polare. Molecule polare – molecula de apă şi molecula de acid clorhidirc.
Fisiunea în lanţ. Reactorul nuclear.
Reacţia de fisiune în lanţ. Criticalitatea fisiunii în lanţ. Reactorul nuclear. Bomba nucleară.
Legătura coordinativă. Combinaţiile complexe.
Legătura coordinativă. Coordinare. Combinații complexe. Donor, acceptor, ion central, ligand. Număr de coordinare.
Forţe intermoleculare. Legături de hidrogen.
Forțe intramoleculare şi forțe intermoleculare. Legătura de hidrogen, forțe dipol-dipol, forțe de dispersie London, forțe van der Waals. Proprietățile influențate de forțele intermoleculare: punct de fierbere, punct de topire, stare de agregare.
Proprietăţile apei
Molecula de apă. Proprietățile apei. Legături de hidrogen. Dipoli. Gheța. Solubilitate, punct de topire, punct de fierbere.
Forţele dipol-dipol şi forţele de dispersie London
Forțe intermoleculare. Legătura de hidrogen, forțe dipol-dipol, forțe de dispersie London, forțe van der Waals. Punct de fierbere, punct de topire, stare de agregare, electronegativitate.
Fuziunea nucleară. TOKAMAK-ul.
Fuziunea nucleară. Reactorul TOKAMAK. Efectul de stricţiune al plasmei.
Valenţa şi numărul de oxidare
Valența, covalența, electrovalența, numărul de oxidare. Electronii de valenţă. Reguli pentru determinarea numerelor de oxidare. Determinarea numerelor de oxidare în funcţie de electronegativitate. Valenţa şi poziţia în tabelul periodic.
Evoluţia stelelor.
Naşterea şi moartea stelelor. Lanţul de fuziune proton-proton.
Acceleratoare liniare de particule.
Acceleratoare de particule. Acceleratorul liniar rezonant. Sincronismul.
Acceleratoare circulare de particule.
Acceleratoare circulare: ciclotronul şi sincrotronul. Radiaţia sincrotronică. Aplicaţii.
Starea gazoasă. Legea gazelor ideale.
Gaze reale. Modelul gazului ideal. Legea gazelor ideale. Parametrii de stare ai gazelor. Valori numerice ale lui R (constanta molară a gazelor ideale). Variaţia parametrilor gazelor ideale. Condensarea.
Legea generală a gazelor
Legea gazelor ideale. Legea lui Avogadro. Parametrii de stare ai gazelor. Ecuaţia lui van der Waals. Aplicaţie.
Modelul standard. Particule elementare.
Modelul standard al interacţiunilor cuantice de câmp. Fizica particulelor elementare.
Soluţii. Dizolvarea compuşilor ionici şi moleculari în apă.
Soluţii. Amestecuri omogene şi amestecuri eterogene. Solvent/dizolvant şi solut/dizolvat/solvat. Soluţii lichide, gazoase şi solide. Solubilitate. Factorii care influenţează solubilitatea. Apa – cel mai bun solvent. Dizolvarea. Dizolvarea compuşilor ionici în apă. Dizolvarea substanţelor polare în apă.
Concentraţia soluţiilor. Cristalohidraţi.
Soluţii. Concentraţia. Concentraţia procentuală şi concetraţia molară. Aplicaţie. Cristalohidraţi. Substanţă anhidră, eflorescenţă, higroscopicitate.
Concentraţia procentuală - aplicaţii
Soluții, dizolvare. Concentrație procentuală. Masă dizolvată, masa soluției. Aplicații.
Concentraţia molară - aplicaţii
Calculul concentraţiei molare a unei soluţii. Regula de trei simplă. Molaritate. Aplicaţii.
Echilibre chimice – legea acţiunii maselor
Reacţia directă, reacţia inversă. Procedeul Haber, obţinerea amoniacului. Starea de echilibru chimic. Variaţia în timp a concetraţiilor şi a vitezelor de reacţie. Reacţii reversibile. Legea acţiunii maselor. Constanta de echilibru. Aplicaţii – legea acţiunii maselor.
Echilibre chimice – aplicaţie
Viteza reacţiei directe, viteza reacţiei inverse. Starea de echilibru chimic. Constanta de echilibru. Aplicaţii.
Factorii care influenţează echilibrele chimice
Principiul lui LeChatelier. Influenţa concentraţiei, a presiunii şi a temperaturii asupra echilibrelor chimice. Reacţii endoterme şi reacţii exoterme. Procedeul Haber-Bosch, obţinerea amoniacului la scală industrială. Reacţii reversibile şi reacţii ireversibile.
Acizi şi baze. Teoria protolitică.
Reacţia de neutralizare. Acizi, baze. Protonul. Transferul de protoni. Ion hidroniu. Teoria Brönsted-Lowry sau teoria protolitică. Clasificarea acizilor. Acid conjugat, bază conjugată. Cupluri acid-bază conjugate.
Tăria acizilor şi bazelor – amfoliţi acido-bazici
Acizi tari şi acizi slabi. Ionizarea acizilor tari. Ionizarea acizilor slabi. Constanta de aciditate. Ka. Baze tari şi baze slabe. Ionizarea bazelor tari. Ionizarea bazelor slabe. Constanta de bazicitate, Kb. Caracterul amfoter. Amfoliţi acido-bazici.
pH-ul soluţiilor apoase
pH – definiţie, semnificaţie matematică. Reacţia de autoprotoliză a apei. Soluţie neutră. Produsul ionic al apei, Kw. Soluţii acide, soluţii neutre şi soluţii bazice. pH neutru, pH bazic şi pH acid. Scala de pH.
Reacţii redox. Oxidanţi şi reducători.
Transferul de electroni. Reacţia de oxidare. Reacţia de reducere. Numărul de oxidare. Reguli pentru determinarea numerelor de oxidare. Reacţii redox. Agenţi oxidanţi şi agenţi reducători. Caracter oxidant şi carcter reducător. Seria activităţii metalelor.
Seria activităţii metalelor
Oxidant, reducător. Metale active, metale foarte active şi metale inactive. Atomi metalici, ioni metalici – configuraţia electronică.
Coeficienţii stoechiometrici în ecuaţiile reacţiilor redox
Coeficienţi stoechiometrici. Stabilirea coeficienţilor stoechiometrici prin metoda redox – aplicaţii.
Celule electrochimice
Electrochimie. Celulă electrochimică. Elemente galvanice/voltaice. Conductori metalici şi electroliţi. Electrod, anod, catod. Semicelulă galvanică. Punte de sare. Procesele chimice care au loc la anod şi la catod. Simbolizarea unei celule electrochimice. Pile uscate/baterii. Pila Daniell.
Coroziunea. Prevenirea coroziunii.
Coroziunea. Reacţiile chimice care generează coroziunea. Metode de prevenire a coroziunii. Galvanizarea. Protecţia catodică.
Transformări de fracții ordinare în fracții zecimale 1
Transformarea fracțiilor ordinare în fracții zecimale. Transformarea fracțiilor ordinare ai căror numitori au in descompunerea lor doar puteri cu baza 2 sau 5.
Mulţimi - noţiuni introductive
Noțiuni introductive privind mulțimile. Relația dintre un element și o mulțime (relația de apartenență). Reprezentarea mulțimilor: cu ajutorul diagramelor, prin enumerarea elementelor și prin enunțarea proprietăților caracteristice elementelor. Mulțimi finite. Mulțimi infinite. Mulțimea vidă. Relații între mulțimi. Submulțimi.
Teorema împărţirii cu rest
Împărțirea cu rest a numerelor naturale. Teorema împarțirii cu rest.
Deîmpărţit = cât x împărţitor + rest, restul < împărţitorul (d = c x î + r, r < î)
Operații cu numere naturale. Ridicarea la putere
Puterea unui număr natural. Ridicarea la putere a unui număr natural. Reguli de calcul cu puteri. Compararea puterilor. Ordonarea puterilor.
Operații cu numere naturale. Ordinea efectuării operațiilor
Ordinea efectuării operaţiilor. Adunarea, scăderea, înmulțirea și împărțirea, ridicarea la putere
Sisteme de numerație
Sistemul de numerație zecimal (baza 10). Sistemul de numerație binar (baza 2). Sistemul de numerație hexazecimal (baza 16). Conversia unui număr dintr-un sistem de numerație în altul.
Divizibilitatea numerelor naturale. Divizor. Multiplu
Divizibilitatea numerelor naturale. Noţiunea de divizor. Noţiunea de multiplu.
Proprietăţile divizibilităţii
Proprietățile divizibilității. Proprietăţi ale relaţiei de divizibilitate în mulțimea numerelor naturale N.
Criterii de divizibilitate
Criteriile de divizibilitate cu 2, 3, 4, 5, 9, 10, 25.
Numere prime. Numere compuse
Un număr prim este un număr natural care are exact doi divizori: numărul 1 și numărul în sine. Un număr compus este orice număr natural care are cel puțin 3 divizori. Algoritmul de verificare a numerelor prime.
Descompunerea unui număr natural în produs de puteri de numere prime
Descompunerea unui număr natural în produs de factori primi.
Cel mai mare divizor comun (c.m.m.d.c.) şi cel mai mic multiplu comun (c.m.m.m.c.)
Noțiunile de cel mai mare divizor comun (c.m.m.d.c) şi cel mai mic multiplu comun (c.m.m.m.c) al numerelor naturale.
Numere prime între ele
Se numesc numere prime între ele acele numere naturale, diferite de zero, care au c.m.m.d.c. = 1.
Modulul unui număr întreg
Noțiunea de modul. Valoarea absolută a unui număr întreg. Numere întregi opuse.
Adunarea şi scăderea numerelor întregi
Operaţii cu numere întregi. Adunarea numerelor întregi. Scăderea numerelor întregi.
Înmulţirea şi împărţirea numerelor întregi
Operaţii cu numere întregi. Înmulţirea numerelor întregi. Împărţirea numerelor întregi. Regula semnelor.
Ordinea efectuării operațiilor cu numere întregi
Operații cu numere întregi.
Puterea cu exponent natural a unui număr întreg
Ridicarea la putere a numerelor întregi și reguli de calcul cu puteri.
Divizibilitatea numerelor întregi
Divizibilitatea numerelor întregi.
Fracţii
Noțiunea de fracție. Identificarea în limbajul cotidian sau în probleme a fracţiilor ordinare.
Fracţii subunitare, echiunitare, supraunitare
Tipuri de fracţii. Clasificarea fracțiilor ordinare în fracții subunitare, fracții echiunitare și fracții supraunitare.
Transformări de fracții ordinare în fracții zecimale 2. Periodicitate
Transformarea fracțiilor ordinare în fracții zecimale. Transformarea fracțiilor ordinare ai căror numitori au în descompunerea lor și puteri cu baza diferită de 2 sau 5. Fracții zecimale periodice.
Amplificarea şi simplificarea fracţiilor
Amplificarea fracțiilor. Simplificarea fracţiilor. Fracții echivalente.
Legătura dintre numitorul unei fracții ordinare ireductibile și numărul zecimal obținut
Modul în care numitorul unei fracții ordinare ireductibile determină obținerea unei fracții zecimale finite sau periodice
Aducerea fracţiilor la acelaşi numitor
Aflarea numitorului comun a două sau mai multe fracții. Aducerea fracțiilor la același numitor.
Adunarea fracțiilor zecimale
Adunarea fracțiilor zecimale care au un număr finit de zecimale nenule
Adunarea fracțiilor ordinare pozitive
Adunarea numerelor raționale pozitive reprezentate de fracții care au același numitor sau numitori diferiți.
Scăderea fracțiilor ordinare pozitive
Scăderea numerelor raționale pozitive reprezentate de fracții care au același numitor sau numitori diferiți.
Înmulţirea fracțiilor ordinare pozitive
Înmulțirea unei fracții cu un număr natural. Aflarea unei fracții dintr-un număr. Înmulţirea numerelor raționale pozitive reprezentate prin fracții ordinare.
Împărțirea fracțiilor ordinare pozitive
Scoaterea întregilor din fracție şi introducerea întregilor în fracţie
Scoaterea întregilor din fracție și introducerea întregilor în fracţie. Reprezentare prin desen
Transformarea fracţiilor ordinare cu numitorul putere a lui 10 în fracţii zecimale
Transformarea fracțiilor ordinare în fracții zecimale. Metode de transformare a fracţiilor ordinare în fracții zecimale.
Scăderea fracțiilor zecimale
Scăderea fracțiilor zecimale care au un număr finit de zecimale nenule
Ordinea efectuării operaţiilor cu numere raționale pozitive
Calcule cu fracţii folosind ordinea efectuării operațiilor.
Înmulțirea numerelor reale (1)
Produsul numerelor reale de forma 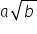 , reguli de calcul cu radicali.
, reguli de calcul cu radicali.
Scoaterea factorilor de sub radical
Calcule cu radicali: scoaterea factorilor de sub radical
Operaţii cu numere reale
Adunarea numerelor reale. Scăderea numerelor reale. Înmulţirea numerelor reale. Împărţirea numerelor reale. Ridicarea la putere a numerelor reale. Calcule cu radicali.
Raţionalizarea numitorului unei fracții (1)
Raţionalizarea numitorului de forma 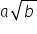
Ecuații de gradul întâi cu două necunoscute
Ecuația de gradul I cu două necunoscute. Reprezentarea geometrică a mulțimii soluțiilor unei ecuații de gradul întâi cu două necunoscute.
Intervale de numere reale
Noțiunea de interval. Intervale mărginite de numere reale, intervale nemărginite. Interval deschis, interval închis. Legătura dintre intervale și modul. Determinarea soluțiilor unor inecuații (în mulțimea numerelor reale) care au necunoscuta în modul.
Media aritmetică, media ponderată, media geometrică
Formulele pentru medie aritmetică, medie ponderată și medie geometrică a numerelor reale. Inegalitatea mediilor.
Rădăcina pătrată a unui număr rațional pozitiv
Noțiunea de radical. Rădăcina pătrată. Extragerea rădăcinii pătrate.
Rotunjirea şi aproximarea unui număr real
Aproximări, rotunjiri. Aproximarea unui număr real. Rotunjirea unui număr real.
Adunarea și scăderea numerelor reale reprezentate prin litere
Operații cu numere reale reprezentate prin litere. Adunarea numerelor reale reprezentate prin litere. Scăderea numerelor reale reprezentate prin litere.
Descompuneri în factori
Descompunerea în factori. Metode de descompunere în factori: metoda factorului comun, formule de calcul prescurtat și metode combinate.
Rapoarte de numere reale reprezentate prin litere
Definirea unui raport algebric. Găsirea domeniului de definiție al unui raport. Amplificarea unui raport. Simplificarea unui raport. Operații cu rapoarte algebrice. Aducerea unei expresii algebrice la forma cea mai simplă.
Ecuații cu numere zecimale
Rezolvarea unor ecuații cu o necunoscută în care apar numere zecimale
Proporţii. Proporţii derivate
Proporţii. Aflarea unui termen necunoscut dintr-o proporţie. Proporţii derivate.
Mărimi direct proporţionale
Rezolvarea problemelor cu mărimi direct proporţioale. Regula de trei simplă pentru mărimi d.p.
Mărimi invers proporționale
Rezolvarea problemelor cu mărimi invers proporţionale. Regula de trei simplă pentru mărimi i.p.
Rapoarte și procente
Raportul a două numere, scara hărții, titlul unui aliaj. Procente, concentrația procentuală
Probabilitatea unui eveniment
Experienţă, eveniment, probabilitatea realizării unui eveniment. Probleme cu probabilități
Secțiuni axiale în corpurile care admit axă de simetrie
Exemple de secțiuni axiale în corpurile geometrice care admit axă de simetrie.
Inecuaţii în mulțimea numerelor reale
Rezolvarea unor inecuații în mulțimea numerelor reale. Scrierea soluției sub formă de interval.
Sisteme de ecuaţii
Definirea unui sistem de ecuații cu două necunoscute. Soluția unui sistem de ecuații cu două necunoscute.
Ecuaţia de gradul al doilea
Forma unei ecuații de gradul doi. Deducerea formulelor care apar în rezolvarea unei ecuații de gradul al doilea.
Probleme care se rezolva cu ajutorul ecuaţiilor (numere naturale)
Etapele rezolvării unei probleme cu ajutorul ecuațiilor.
Funcții: definiție, terminologie
Definirea noțiunii de funcție. Domeniul de definiție. Codomeniu. Lege de corespondență.
Mulțimea valorilor unei funcții
Imaginea unei funcției (sau mulțimea de valori a funcției). Legătura dintre imaginea unei funcții și codomeniul său.
Funcţii liniare
Funcție liniară. Trasarea graficului unei funcții liniare. Intersecția dintre graficul unei funcții și axele de coordonate.
Graficul unei funcții
Graficul funcției definite pe o mulțime finită. Reprezentarea geometrică a unui grafic funcție. Citirea unui grafic dat.
Instrumente geometrice: riglă, echer, raportor, compas
Utilizarea instrumentelor geometrice: riglă, echer, raportor, compas.
Punct, dreaptă, semidreaptă, segment, plan, semiplan
Noţiuni elementare în geometrie. Punct, dreaptă, semidreaptă, segment, plan, semiplan.
Pozițiile relative ale unui punct față de o dreaptă. Puncte coliniare
Poziţiile relative ale unui punct faţă de o dreaptă. Puncte coliniare. Puncte necoliniare.
Poziţiile relative a două drepte. Drepte coplanare și necoplanare
Poziţiile relative a două drepte în plan. Drepte coplanare: drepte confundate, drepte secante (drepte concurente), drepte paralele. Drepte necoplanare (drepte in plane diferite).
Lungimea unui segment. Segmente congruente
Distanţa dintre două puncte, lungimea unui segment, segmente congruente. Mijlocul unui segment.
Unghiuri. Clasificarea unghiurilor
Unghi ascuţit, unghi drept, unghi obtuz, unghi nul, unghi alungit.
Unghiuri adiacente. Bisectoarea unui unghi
Unghiuri adiacente. Bisectoarea unui unghi. Unghiuri congruente.
Unghiuri suplementare. Unghiuri complementare
Unghiuri complementare şi suplementare.
Unghiuri opuse la vârf
Două unghiuri se numesc unghiuri opuse la vârf dacă laturile lor sunt perechi de semidrepte opuse
Unghiuri în jurul unui punct
Suma unghiurilor formate în jurul unui punct este de 360 grade
Triunghiul
Definiţia unui triunghi. Elementele unui triunghi. Noțiunea de perimetru triunghi, semiperimetru. Suma măsurilor unghiurilor unui triunghi. Unghi exterior unui triunghi.
Clasificarea triunghiurilor
Clasificarea triunghiurilor după laturi şi după unghiuri: triunghi oarecare, triunghi isoscel, triunghi echilateral, triunghi ascuţitunghic, triunghi dreptunghic, triunghi obtuzunghic
Congruenţa triunghiurilor
Triunghiuri congruente. Cazurile de congruenţă ale triunghiurilor oarecare
Metoda triunghiurilor congruente - aplicaţii
Pentru a demonstra că două segmente sau unghiuri sunt congruente, căutăm să le încadrăm în două triunghiuri a căror congruenţă poate fi demonstrată. Triunghiuri congruente.
Drepte perpendiculare. Distanţa de la un punct la o dreaptă
Drepte perpendiculare. Distanţa de la un punct la o dreaptă. Două drepte concurente care formează un unghi drept se numesc drepte perpendiculare.
Criteriile de congruenţă ale triunghiurilor dreptunghice
Congruenţa triunghiurilor dreptunghice. Criteriile de congruenţă ale triunghiurilor dreptunghice
Mediatoarea unui segment. Concurenta mediatoarelor laturilor unui triunghi
Linii importante în triunghi: mediatoarea, concurența mediatoarelor. Centrul cercului circumscris triunghiului. Proprietatea punctelor situate pe mediatoarea unui segment. Noțiunea de 'Teoremă directă' și 'Teoremă reciprocă'
Bisectoarea unui unghi. Concurența bisectoarelor unghiurilor unui triunghi
Linii importante în triunghi: bisectoarea, concurența bisectoarelor. Proprietatea punctelor situate pe bisectoarea unui unghi. Centrul cercului înscris în triunghi.
Drepte paralele. Criterii de paralelism
Drepte paralele tăiate de o secantă. Unghiuri alterne interne. Unghiuri alterne externe. Unghiuri corespondente. Unghiuri interne de aceeaşi parte a secantei. Unghiuri externe de aceeaşi parte a secantei. Axioma lui Euclid. Distanța dintre două drepte paralele.
Drepte paralele intersectate de o secantă
Drepte paralele intersectate de o secantă. Unghiuri alterne interne. Unghiuri alterne externe. Unghiuri corespondente. Unghiuri interne de aceeaşi parte a secantei. Unghiuri externe de aceeaşi parte a secantei.
Proprietați ale triunghiurilor oarecare
Suma masurilor unghiurilor unui triunghi este de 180 de grade. Unghi exterior unui triunghi.Teorema unghiului exterior. Bisectoarea interioară și bisectoarea exterioară a unui triunghi. Relații între unghiurile și laturile unui triunghi.
Mediana în triunghi. Concurența medianelor laturilor unui triunghi
Linii importante în triunghi: mediana, concurența medianelor unui triunghi. Centru de greutate al triunghiului. Mediana împarte un triunghi în două triunghiuri echivalente.
Proprietăţile triunghiului isoscel
Proprietăţile triunghiului isoscel. Un triunghi isoscel are două unghiuri congruente. Într-un triunghi isoscel, mediana, înălțimea, bisectoarea și mediatoarea corespunzătoare bazei coincid.
Proprietăţile triunghiului echilateral
Triunghiul echilateral. Un triunghi echilateral are toate unghiurile congruente. Într-un triunghi echilateral, toate liniile importante ce pornesc din același vârf coincid.
Proprietăţile triunghiului dreptunghic
Triunghiul dreptunghic. Proprietăţile triunghiului dreptunghic. Mediana într-un triunghi dreptunghic este jumătate din ipotenuză. Cateta opusă unghiului de 30 de grade este jumătate din ipotenuză
Patrulatere convexe
Patrulater convex. Patrulater concav. Suma măsurilor unghiurilor unui patrulater convex este de 360 de grade
Paralelogramul
Patrulaterul convex care are laturile opuse paralele se numește paralelogram. Proprietățile paralelogramului. Modalități de a demonstra că un patrulater este paralelogram.
Dreptunghiul
Paralelogramul care are un unghi drept se numește dreptunghi. Proprietățile dreptunghiului. Modalități de a demonstra că un patrulater este dreptunghi.
Rombul
Paralelogramul care are două laturi consecutive congruente se numește romb. Proprietățile rombului. Modalități de a demonstra că un patrulater este romb.
Pătratul
Un paralelogram care este și dreptunghi și romb se numește pătrat. Proprietățile pătratului. Modalități de a demonstra că un patrulater este pătrat.
Trapezul
Patrulaterul care are două laturi opuse paralele, iar celelalte două neparalele se numește trapez. Definiția unui trapez isoscel. Proprietățile trapezului isoscel. Modalități de a demonstra că un trapez este isoscel.
Centrul de simetrie şi axe de simetrie pentru patrulaterele studiate
Centru de simetrie şi axe de simetrie pentru patrulaterele studiate.
Teorema paralelelor echidistante
Teorema paralelelor echidistante.
Teorema lui Thales
Teorema lui Thales: O paralelă dusă la una din laturile unui triunghi determină pe celelalte două laturi (sau pe prelungirile acestora) segmente proporţionale.
Teorema reciprocă a Teoremei lui Thales
Folosim reciproca Teoremei lui Thales pentru a demonstra că două drepte sunt paralele.
Linia mijlocie în triunghi
Linie mijlocie în triunghi este un segment care uneşte mijloacele a două laturi ale triunghiului. Proprietățile liniei mijlocii.
Linia mijlocie în trapez
Segmentul care uneşte mijloacele laturilor neparalele ale unui trapez se numeşte linie mijlocie a trapezului.
Triunghiuri asemenea
Două triunghiuri se numesc triunghiuri asemenea dacă au toate laturile respectiv proporţionale şi toate unghiurile respectiv congruente
Teorema fundamentală a asemănării
O paralelă la una din laturile unui triunghi formează cu celelalte două laturi (sau cu prelungirile lor) un triunghi asemenea cu cel dat.
Criterii de asemănare a triunghiurilor
U.U., L.U.L., L.L.L; Raportul ariilor a două triunghiuri asemenea.
Proiecţii ortogonale pe o dreaptă
Proiecţia ortogonală a unui punct pe o dreaptă, proiecția ortogonală a unui segment pe o dreaptă
Teorema înălţimii
Într-un triunghi dreptunghic, lungimea înălțimii corespunzătoare unghiului drept este medie proporțională între lungimile proiecțiilor catetelor pe ipotenuză. Teorema înălțimii și reciproca.
Teorema catetei
Într-un triunghi dreptunghic, lungimea unei catete este medie proporțională între lungimea proiecției sale pe ipotenuză şi lungimea ipotenuzei.Teorema catetei și reciproca.
Teorema lui Pitagora
Într-un triunghi dreptunghic, suma pătratelor lungimilor catetelor este egală cu pătratul lungimii ipotenuzei.
Reciproca teoremei lui Pitagora
Dacă într-un triunghi pătratul lungimii unei laturi este egal cu suma pătratelor lungimilor celorlalte două laturi atunci triunghiul este dreptunghic.
Noţiuni de trigonometrie în triunghiul dreptunghic
Funcții trigonometrice: sinus, cosinus, tangentă, cotangentă.
Valorile funcţiilor trigonometrice ale unghiurilor de 30, 45, 60 grade
Valorile funcţiilor trigonometrice pentru unghiuri uzuale.
Rezolvarea triunghiului dreptunghic
Rezolvarea triunghiului dreptunghic folosind funcții trigonometrice și teorema lui Pitagora.
Cercul- definiție, elemente
Definiția cercului. Elementele unui cerc: rază, diametru, coardă. Centrul cercului. Arc de cerc. Semicerc. Puncte diametral opuse. Definiția unui disc.
Unghi la centru
Unghi cu vârful în centrul cercului. Măsura unui unghi la centru. Măsura unui arc de cerc. Arce congruente.
Coarde şi arce in cerc
Teoreme referitoare la coarde și arce în cerc. Coarde congruente. Arce congruente. Diametru perpendicular pe o coardă.
Unghi înscris în cerc
Unghi cu vârful pe cerc. Măsura unui unghi înscris în cerc. Unghi înscris în semicerc. Triunghi înscris în cerc.
Patrulater înscris în cerc; patrulater inscriptibil
Un patrulater se numește patrulater înscris în cerc dacă vârfurile sale aparțin cercului. În acest caz cercul se numește cerc circumscris patrulaterului. Proprietatea unui patrulater înscris în cerc. Patrulater inscriptibil.
Pozitiile relative ale unei drepte faţă de un cerc
Dreaptă exterioară cercului. Tangenta la cerc. Punct de tangență. Dreaptă secantă față de cerc. Tangenta dintr-un punct exterior la un cerc. Triunghi circumscris unui cerc.
Poligoane regulate (înscrise în cerc). Calculul elementelor în poligoane regulate
Măsura unui unghi al unui poligon regulat cu n laturi. Măsura unghiului la centru al unui poligon cu n laturi. Latura și apotema unui poligon. Suma măsurilor unghiurilor unui poligon convex. Măsura unui unghi al unui poligon regulat. Formula pentru arie poligon regulat, în funcţie de raza cercului circumscris.
Introducere în geometria în spaţiu
Noțiunile de bază ale geometriei în spațiu și relațiile care se stabilesc între ele.
Reprezentarea dreptelor paralele, a unghiurilor și a lungimilor segmentelor
Precizări legate de construcția dreptelor și a unghiurilor în spațiu. "Deformarea" unghiurilor, a dreptelor și a lungimilor segmentelor în spațiu
Tetraedrul
Descrierea tetraedrului. Elementele unui tetraedru. Desfășurarea tetraedrului.Tetraedru regulat.
Paralelipipedul dreptunghic
Descrierea unui paralelipiped dreptunghic. Elementele unui paralelipiped dreptunghic. Diagonala paralelipipedului. Desfășurarea paralelipipedului.
Teoreme de paralelism
Enunțarea unor teoreme importante de paralelism în spațiu. Modalități de a demonstra că două plane sunt paralele.
Dreaptă perpendiculară pe plan
Modalități de a demonstra că o dreaptă este perpendiculară pe un plan. Definiția unei drepte perpendiculare pe un plan.
Teoreme de perpendicularitate
Enunțarea unor teoreme de perpendicularitate. Cum arătăm că o dreaptă este perpendiculară pe un plan
Distanţe în spațiu. Perpendiculare și oblice.
Distanța dintre două puncte. Distanța dintre un punct și o dreaptă. Distanța dintre un punct și un plan. Distanța dintre două plane. Oblică la plan.
Secțiuni paralele cu baza în corpuri geometrice
Secțiune în corp geometric. Secțiuni paralele cu baza în prismă. Secțiuni paralele cu baza în corpuri rotunde. Secțiuni paralele cu baza în piramide.
Trunchiul de piramidă (definiție, elemente)
Trunchi de piramidă. Definiția și elementele trunchiului de piramidă. Înălțimea trunchiului. Apotema trunchiului. Apotema bazei mari, apotema bazei mici. Trunchi de piramidă patrulateră regulată. Trunchi de piramidă triunghiulară regulată.
Corpuri geometrice asemenea
Corpuri asemenea. Definiția a două piramide asemenea. Raport de asemănare. Raportul ariilor a două suprafețe omoloage. Raportul volumelor a două piramide asemenea.
Poziții relative a două drepte în spațiu
Stabilirea pozițiilor relative a două drepte în spațiu. Drepte paralele, drepte concurente, drepte necoplanare.
Relația de paralelism
Relația de paralelism. Teorema de tranzitivitate a relației de paralelism în spațiu.
Unghiuri în spațiu (Unghiuri cu laturile respectiv paralele)
Teorema unghiurilor cu laturile respectiv paralele. Unghiul a două drepte concurente
Unghiuri în spațiu (Unghiul a două drepte în spațiu)
Unghiul format de două drepte paralele, concurente sau necoplanare. Determinarea măsurii unghiului format de două drepte necoplanare.
Poziții relative ale unei drepte față de un plan
Dreaptă inclusă în plan, dreaptă secantă unui plan, dreaptă paralelă cu un plan. Cum demonstrăm că o dreaptă este paralelă cu un plan
Poziții relative a două plane
Plane confundate, plane secante, plane paralele. Cum demonstrăm că două plane sunt confundate sau secante sau paralele
Unghiul unei drepte cu un plan
Unghiul dintre o dreaptă și un plan. Măsura unghiului format de o dreaptă cu un plan.
Piramida patrulateră regulată
Descrierea piramidei patrulatere regulate. Elementele unei piramide patrulatere. Înalțimea piramidei. Apotema piramidei. Apotema bazei. Desfășurarea piramidei patrulatere.
Prisma
Descrierea prismei. Elementele unei prisme. Înălțimea prismei. Prisma dreaptă. Prisma oblică. Desfășurarea prismei.
Cubul
Descrierea cubului. Elementele unui cub. Diagonala cubului. Desfășurarea cubului.
Piramida triunghiulară regulată
Descrierea piramidei triunghiulare regulate. Elementele unei piramide triunghiulare. Înalțimea piramidei. Apotema piramidei. Apotema bazei. Desfășurarea piramidei triunghiulare.
Aria triunghiului
Formula pentru arie triunghi. Aria triunghiului oarecare și aria triunghiului dreptunghic.
Alcani – nomenclatură, proprietăţi fizice, aplicaţii practice
Alcani, izoalcani. Metan, etan, propan, butan, izobutan. Izomerie de catenă. Serie omoloagă. Corelaţia dintre structura alcanilor şi proprietăţile fizice (starea de agregare, temperatura de fierbere).
Alcani – proprietăţi chimice
Reacţii care au loc cu scindarea legăturilor C – C. Reacţii care au loc cu scindarea legăturilor C – H. Arderea alcanilor. Reacţia de substituţie – halogenarea alcanilor. Reacţia de dehidrogenare – piroliza, cracarea. Izomerizarea alcanilor. Izomerizarea n-butanului. Cifra octanică a benzinelor. Solubilitatea alcanilor.
Alchene – nomenclatură, proprietăţi fizice, aplicaţii practice
Serie omoloagă. Nomenclatură. Atomi de carbon vinilici şi atomi de carbon alilici. Caracteristicile legăturii duble. Izomerie geometrică (izomeri cis-trans). Izomerie de catenă. Izomerie de funcţiune. Izomerie de poziţie. Proprietăţi fizice
Alchene – proprietăţi chimice
Reacţii specifice hidrocarburilor nesaturate – reacţii de adiţie, de oxidare şi de polimerizare. Hidrogenarea alchenelor, halogenarea alchenelor, adiţia hidracizilor la alchene, adiţia apei la alchene. Oxidare blândă şi oxidare energică. Reacţii comune cu hidrocarburile saturate – reacţii de ardere, reacţii de substituţie. Regula lui Markovnikov. Polimeri vinilici.
Alchine – nomenclatură, proprietăţi fizice
Caracteristicile legăturilor covalente triple. Nomenclatură. Izomerie de constituţie – izomerie de catenă şi izomerie de poziţie. Structura alchinelor. Proprietăţi fizice.
Alchine – proprietăţi chimice
Hidrogenarea acetilenei. Adiţia halogenilor. Adiţia apei. Tautomerizare. Adiţia hidracizilor. Dimerizarea şi trimerizarea acetilenei. Obţinerea vinilacetilenei şi a benzenului. Reacţii de substituţie.
Alcadiene – nomenclatură, proprietăţi fizice şi chimice
Nomenclatură. Clasificarea alcadienelor în funcţie de poziţia legăturilor duble în catenă. Adiţia hidrogenului. Adiţia halogenilor. Adiţia 1,2 şi adiţia 1,4. Reacţia de polimerizare. Reacţia de copolimerizare. Obţinerea butadienei şi a izoprenului.
Arene – nomenclatură, clasificare şi proprietăţi fizice
Hidrocarburi aromatice. Structuri de rezonanţă (structuri limită). Benzenul. Modelul Kékulé. Structura inelului benzenic. Caracter aromatic. Clasificarea arenelor. Nomenclatură. Poziţiile orto-, meta-, şi para-. Proprietăţi fizice.
Arene – proprietăţi chimice (substituţie la nucleul aromatic)
Reacţiile specifice hidrocarburilor aromatice. Reacţii de substituţie la nucleul benzenic. Orientarea reacţiilor de substituţie. Substituenţi de gradul I. Substituenţi de gradul II. Nitrarea toluenului. Reacţia de halogenare a benzenului şi a naftalinei. Reacţia de sulfonare a benzenului şi a naftalinei. Reacţia de alchilare Friedel – Crafts. Reacţia de acilare Friedel – Crafts.
Arene – adiţie la nucleul aromatic, reacţii la catena laterală
Reacţia de hidrogenare a benzenului, a naftalinei şi a antracenului. Reacţii caracteristice catenei laterale – halogenarea şi oxidarea. Poziţia benzilică. Oxidare blândă şi oxidare energică.
Chimia carbonului – chimia organică
Carbonul – “elementul vieţii”. Diferenţa dintre compuşii organici şi compuşii anorganici. Obiectul de studiu al chimiei organice. Elemente organogene. Hidrocarburi. Compuşi organici cu funcţiuni.
Legături covalente în compuşii organici
Tipuri de catene de atomi de carbon. Tipuri de legături covalente în compuşii organici. Orbitali moleculari de legătură. Hibridizare. Orbitali hibrizi. Hibridizare sp3. Hibridizare sp2. Hibridizare sp. Caracteristicile legăturilor covalente. Legătură σ, legătură π, geometrie tetraedrică, geometrie trigonal-planară, geometrie liniară.
Catene de atomi de carbon – clasificarea compuşilor organici
Compuşi organici saturaţi. Compuşi organici nesaturaţi. Atom de carbon primar, secundar, terţiar, cuaternar. Clasificarea compuşilor organici.
Structura compuşilor organici – formule moleculare şi formule structurale
Structură chimică. Analiza elementală. Determinarea formulei procentuale, a formulei brute şi a formulei moleculare (exemple de calcul). Formule structurale: formule de proiecţie, formule de proiecţie restrânse (plane). Izomerie. Izomeri geometrici (izomeri cis-trans).
Reacţii ale compuşilor organici
Clasificarea reacţiilor chimice ale compuşilor organici. Schema generală a unei reacţii. Substrat organic şi reactant. Reacţii de substituţie. Reacţii de adiţie. Reacţii de eliminare. Reacţii de transpoziţie.
Reacţii de halogenare
Halogenarea prin reacţii de substituţie – halogenarea alcanilor, halogenarea în poziţie alilică, halogenarea în poziţie benzilică, halogenarea nucleului aromatic. Halogenarea prin reacţii de adiţie – adiţia halogenilor la alchene, adiţia halogenilor la alchine, adiţia halogenilor la alcadiene, adiţia halogenilor la benzen, adiţia hidracizilor la alchene, adiţia hidracizilor la alchine.
Reacţii de alchilare
Agenţi de alchilare. Alchilarea Friedel-Crafts. Alchilarea arenelor cu alchene. Alchilarea aminelor. Alchilări cu oxid de etenă. Obţinerea oxidului de etenă. Alchilarea aminelor cu oxid de etenă. Alchilarea alcoolilor cu oxid de etenă.
Reacţii de polimerizare
Importanţa reacţiilor de polimerizare. Schema generală a unei reacţii de polimerizare. Proprietăţile polimerilor. Procedee de polimerizare – polimerizare radicalică, reacţia de policondensare. Radicali liberi. Polimerizarea radicalică. Polimeri vinilici. Reacţia de coplimerizare. Copolimeri.
Reacţii de esterificare
Obţinerea esterilor. Derivaţi funcţionali ai acizilor carboxilici. Aplicaţii industriale ale reacţiilor de esterificare. Obţinerea aspirinei. Acidul acetilsalicilic.
Reacţii de hidroliză
Hidroliza compuşilor halogenaţi – hidroliza compuşilor monohalogenaţi, a compuşilor dihalogenaţi geminali şi a compuşilor trihalogenaţi geminali. Hidroliza esterilor în mediu acid. Hidroliza esterilor în mediu bazic. Hidroliza trigliceridelor.
Reacţii de condensare şi policondensare
Reacţii de condensare între compuşii carbonilici – condensarea aldolică şi crotonică. Componentă carbonilică şi componentă metilenică. Reacţii de policondensare. Obţinerea şi proprietăţile fenoplastelor – bachelita şi novolacul.
Izomerie optică – chiralitatea
Clasificarea izomerilor în izomeri de constituţie şi stereoizomeri. Clasificarea stereoizomerilor în izomeri de conformaţie şi izomeri de configuraţie. Clasificarea izomerilor de configuraţie în enantiomeri şi diastereoizomeri. Chiralitate. Obiecte chirale şi obiecte achirale. Atom de carbon asimetric. Centru de chiralitate. Molecule chirale şi molecule achirale. Enantiomeri
Configuraţia enantiomerilor. Formule de perspectivă, formule Fischer
Formule de perspectivă. Formule de proiecţie Fischer. Configuraţia enantiomerilor. Sistemul R, S. Denumirea enantiomerilor reprezentaţi prin formule de perspectivă. Denumirea enantiomerilor reprezentaţi prin formule de proiecţie Fischer.
Alcooli – metanol, etanol, glicerină.
Clasificarea compuşilor organici cu funcţiuni. Alcool. Grupa funcţională hidroxil. Nomenclatură. Clasificarea alcoolilor. Structură. Proprietăţi fizice. Metanol şi etanol – acţiune biologică. Obţinerea etanolului – fermentaţia alcoolică. Glicerina, trinitratul de glicerină. Dinamita şi Premiile Nobel.
Acizi carboxilici. Acidul acetic.
Caracteristicile şi structura grupei funcţionale carboxil. Obţinerea acidului acetic/oţetului de vin – fermentaţia acetică. Proprietăţile fizice şi chimice ale acidului acetic. Reacţia cu metale active, cu oxizi metalici, cu sărurile acidului carbonic şi cu hidroxizii alcalini. Reacţia de esterificare.
Grăsimi
Acizii graşi saturaţi. Acizi graşi nesaturaţi. Trigliceride simple şi mixte. Grăsimi saturate. Grăsimi nesaturate. Grăsimi mononesaturate. Omega 3. Grăsimi trans. Acţiunea grăsimilor asupra organismului uman.
Săpunuri şi detergenţi
Reacţia de saponificare. Agenţi activi de suprafaţă (surfactanţi). Clasificarea şi structura surfactanţilor. Modul de acţiune al săpunurilor şi detergenţilor. Clasificarea detergenţilor.
Alcooli – proprietăţi chimice
Caracteristicile grupei funcţionale hidroxil. Reacţia cu metalele alcaline. Reacţia de deshidratare (eliminarea apei). Reactivitatea alcoolilor în funţie de structură. Deshidratarea intramoleculară şi deshidratarea intermoleculară a alcoolilor. Obţinerea eterilor. Oxidarea alcoolilor – oxidarea blândă şi oxidarea energică. Reacţia de esterificare – esteri organici şi esteri anorganici.
Fenoli
Clasificarea fenolilor. Nomenclatură. Caracteristicile grupei hidroxil fenolice. Proprietăţi fizice. Proprietăţi chimice – reacţii specifice grupei hidroxil şi reacţii specifice nucleului aromatic. Reacţia cu metalele alcaline. Reacţia cu hidroxizii alcalini. Reacţii de substituţie la nucleul aromatic – reacţia de sulfonare şi reacţia de nitrare a fenolului. Aplicaţii practice.
Derivaţi halogenaţi – importanţă, proprietăţi fizice
Aplicaţii practice ale derivaţilor halogenaţi. Clasificare. Nomenclatură. Caracteristicile legăturilor C – halogen. Proprietăţi fizice. Obţinere.
Derivaţi halogenaţi – proprietăţi chimice
Derivaţi halogenaţi cu reactivitate normală, derivaţi halogenaţi cu reactivitate mărită şi derivaţi halogenaţi cu reactivitate scăzută. Reacţii de substituţie – reacţia de hidroliză, reacţia cu cianurile alcaline. Reacţia de dehidrohalogenare (de eliminare a hidracidului). Regula lui Zaiţev.
Amine
Clasificarea şi nomenclatura aminelor. Caracteristicile grupei funcţionale amino. Proprietăţi fizice. Caracterul bazic al aminelor. Amine aromatice. Reacţii de substituţie. Reacţii de alchilare. Obţinerea sărurilor de arendiazoniu. Aplicaţii practice.
Compuşi carbonilici
Grupa funcţională carbonil. Aldehide şi cetone. Nomenclatura aldehidelor. Nomenclatura cetonelor. Proprietăţi fizice. Reacţii de adiţie – adiţia hidrogenului. Reacţii de oxidare. Aplicaţii practice.
Zaharide - Glucoza
Compuşi organici cu acţiune biologică. Compuşi cu mai multe grupe funcţionale. Zaharide – polihidroxialdehide şi polihidroxicetone. Monozaharide. Zaharide de policondensare. Glucoza. Structura zaharidelor. Proiecţii Fischer – notaţii D şi L. Atom de carbon asimetric. Importanţa biologică a glucozei. Aplicaţiile practice ale glucozei.
Zaharide – produşi de policondensare ai monozaharidelor
Zaharoza – carcateristici şi aplicaţii practice. Zahăr rafinat şi zahăr nerafinat. Amidonul. Amiloza şi amilopectina. Surse de amidon. Fotosinteza. Celuloza. Surse de celuloză. Proprietăţi şi aplicaţii practice.
Proteine
Aminoacizi – structură şi nomenclatură. Peptide şi polipeptide. Reacţia de policondensare a aminoacizilor. Legătura peptidică. Clasificarea proteinelor. Funcţii. Proprietăţi fizice. Proteine simple şi proteine conjugate. Grupe prostetice. Denaturarea proteinelor. Factori denaturanţi.
Aria dreptunghiului
Formula pentru arie dreptunghi. Exercițiu cu aria unui dreptunghi.
Aria cercului (discului); Aria sectorului de cerc
Formula de calcul pentru aria cercului. Aria discului. Aria sectorului de cerc. Exemplu de calcul pentru aria cercului.
Enantiomeri - proprietăţi, importanţă. Diastereoizomeri
Interacţiunea enantiomerilor cu lumina polarizată. Activitate optică. Substanţe optic active - izomeri optici, antipozi optici. Polarimetru. Dextrogir, levogir, amestec racemic. Compuşi cu două centre de chiralitate. Diastereoizomeri. Proprietăţi fizice şi chimice ale enantiomerilor. Acţiunea fiziologică a enantiomerilor. (R) - talidomidă, (S) - talidomidă.
Aminoacizi
Proteine, peptide, aminoacizi. Legătură peptidică, rest de aminoacid. Cei 20 de aminoacizi naturali. Structura aminoacizilor. Sistemul D, L. Aminoacizii - seria sterică L. Reacţii stereospecifice. Proprietăţi chimice ale aminoacizilor. Amfion (formă dipolară). Clasificarea aminoacizilor în funcţie de polaritatea radicalului hidrocarbonat. Caracterul amfoter al aminoacizilor. Soluţii tampon.
Proteine - structura primară
Proteine - polimeri ai aminoacizilor. Policondensarea aminoacizilor. Hidroliza proteinelor. Structura proteinelor. Structura primară - secvenţa resturilor de aminoacizi. Corelaţia structură - funcţie. Conformaţie. Legătura peptidică - proprietăţi.
Proteine - structura secundară, terţiară şi cuaternară
Structura secundară - helix α, foi pliate β, structuri secundare nedefinite. Orientarea în spaţiu a proteinelor. Interacţiuni intramoleculare care stabilizează structura secundară. Structura terţiară. Interacţiuni care stabilizează structura terţiară a proteinelor. Protomeri. Structura cuaternară. Clasificarea proteinelor în funcţie de structură. Denaturarea proteinelor.
Zaharide
Fotosintesză, respiraţie. Funcţia zaharidelor în organismele vii. Monozaharide - aldoze, cetoze. D-glucoza, D-fructoza, D-riboza. Formule de proiecţie Fischer. Strucutra ciclică a D-glucozei şi D-ribozei. Adiţie intramoleculară. Semiacetali, semicetali. Anomer α, anomer β, mutarotaţie, centru anomeric. Ciclu piranozic, ciclu furanozic. Formule Haworth. Hidroxil glicozidic. Dizaharide - zaharoză. Polizaharide - amidon, celuloză.
Acizi nucleici - mononucleotide, polinucleotide
Secvenţă de nucleotide. Acid deoxiribonucleic (ADN) şi acid ribonucleic (ARN). Informaţie genetică. Structura acizilor nucleici. Mononucleotide - pentoză, acid fosforic, baze azotate. Baze purinice şi baze pirimidinice. Riboză şi deoxiriboză. Nucleozide. Policondensarea mononucleotidelor.
Acizi nucleici - ADN, ARN, codul genetic
Structura de dublu helix a ADN-ului. Perechi de baze complementare în ADN şi perechi de baze complementare in ARN. Secvenţa mononucleotidelor. ARN mesager, ARN de transport, ARN ribozomal. Sinteza proteinelor - transcriere, traducere. Cod genetic, codon, genă, universalitatea codului genetic.
Ridicarea la putere a fracțiilor ordinare pozitive
Puterea cu exponent natural a unui număr rațional pozitiv. Reguli de calcul cu puteri.
Media aritmetică și media aritmetică ponderată
Formulele pentru medie aritmetică și medie ponderată a numerelor raționale pozitive.
Ecuații în mulțimea numerelor raționale pozitive
Rezolvarea ecuațiilor în mulțimea numerelor raționale pozitive. Probleme care se rezolvă cu ajutorul ecuațiilor
Elemente de organizare a datelor
Reprezentarea și interpretarea unor dependențe funcționale prin tabele și diagrame
Mulțimea numerelor întregi. Axa numerelor
Mulțimea numerelor întregi. Numere întregi pozitive și negative. Reprezentarea pe axă a numerelor întregi.
Ecuații în mulțimea numerelor întregi
Rezolvarea ecuațiilor în mulțimea numerelor întregi
Inecuații în mulțimea numerelor întregi
Rezolvarea inecuațiilor în mulțimea numerelor întregi. Inecuații cu modul
Înălțimea în triunghi. Concurența înălțimilor
Linii importante în triunghi: înălțimea, concurența înălțimilor. Ortocentru.
Simetria față de o dreaptă
Simetricul unui punct față de un punct. Simetricul unui punct față de o dreaptă. Axa de simetrie. Simetrica unei figuri față de o axă
Înmulțirea numerelor raționale
Înmulțirea numerelor raționale scrise sub formă de fracție ordinară.
Împărțirea numerelor raționale
Împărțirea numerelor raționale scrise sub formă de fracție ordinară.
Ridicarea la putere a numerelor raționale
Ridicarea la putere a numerelor raționale, reguli de calcul cu puteri.
Ordinea efectuării operațiilor cu numere raționale
Exerciții cu fracții folosind ordinea efectuării operațiilor.
Împărțirea numerelor reale (1)
Împărțirea numerelor reale de forma 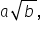 reguli de calcul cu radicali.
reguli de calcul cu radicali.
Ridicarea la putere a numerelor reale
Puterea cu exponent întreg a unui numar real. Reguli de calcul cu puteri.
Înmulțirea, împărțirea și ridicarea la putere a numerelor reale reprezentate prin litere
Operații cu numere reale reprezentate prin litere. Înmulțirea numerelor reale reprezentate prin litere. Împărțirea numerelor reale reprezentate prin litere. Ridicarea la putere a numerelor reale reprezentate prin litere.
Mulțimea numerelor reale
Număr real. Mulțimea numerelor reale. Definiția unui număr irațional. Numere iraționale. Relația de incluziune dintre mulțimile N, Z, Q, R.
Axa numerelor reale. Ordonare
Reprezentarea numerelor reale pe axa numerelor. Ordonarea numerelor reale. Partea întreagă a unui număr real. Partea fracționară a unui număr real.
Adunarea numerelor reale (1)
Adunarea numerelor reale de forma 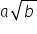 , calcule cu radicali
, calcule cu radicali
Scăderea numerelor reale (1)
Scăderea numerelor reale de forma 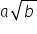 , calcule cu radicali
, calcule cu radicali
Introducerea factorilor sub radical
Calcule cu radicali: introducerea factorilor sub radical
Ecuații în mulțimea numerelor reale
Rezolvarea ecuațiilor în mulțimea numerelor reale. Ecuații de gradul I. Ecuații simple de gradul al II-lea.
Inecuații cu coeficienți reali
Inecuații de gradul I cu coeficienți reali.
Produsul cartezian a două mulțimi
Elemente de organizare a datelor. Produs cartezian a două mulțimi. Sistem de axe ortogonale.
Mulțimea numerelor raționale
Numere raționale. Mulțimea numerelor raționale. Forme de scriere a unui număr rațional. Transformarea fracțiilor ordinare în fracții zecimale.
Opusul unui numar rațional
Opusul unui numar rațional. Numere raționale opuse.
Valoarea absolută a unui numar rațional
Modulul unui numar rațional. Proprietățile modulului.
Ordonarea numerelor raționale
Compararea fracțiilor ordinare având același numitor sau numitori diferiți. Compararea a două fracții cu același semn sau cu semne diferite. Ordonarea numerelor raționale. Partea întreagă și partea fracționară a unui număr rațional.
Adunarea numerelor raționale
Adunarea numerelor raționale având același semn sau semne diferite.
Scăderea numerelor raționale
Scăderea numerelor raționale având același semn sau semne diferite.
Aria pătratului
Formula pentru arie pătrat. Exercițiu cu aria unui pătrat.
Punct, dreaptă, plan.
Noțiuni primare de geometrie plană. Punct, dreaptă, semidreaptă, segment. Plan, semiplan.
Segmentul. Lungimea unui segment.
Segmentul, lungimea unui segment, segmente congruente.
Unghiuri - definiție și clasificare
Clasificarea unghiurilor. Unghi nul, unghi alungit, unghi ascuțit, unghi obtuz, unghi drept.
Poligoane
Linii frânte, poligoane. Elementele unui poligon: laturi, vârfuri, unghiuri, diagonale.
Triunghiul
Triunghiul. Definiția triunghiului. Elementele unui triunghi.
Patrulatere
Pătrat, dreptunghi, romb, paralelogram, trapez. Prezentare prin descriere și desen.
Cercul
Linii curbe. Cercul. Elmentele unui cerc. Centrul cercului. Raza cercului. Diametrul cercului.
Corpuri geometrice
Cubul, paralelipipedul dreptunghic, piramida, cilindrul, conul, sfera. Recunoașterea elementelor: muchii, fețe, vârfuri.
Unități de măsură pentru lungimi. Transformări.
Unități de masură pentru lungime. Metrul. Multiplii și submultiplii metrului.
Perimetre
Perimetrul unui poligon. Perimetrul triunghiului. Perimetrul pătratului. Perimetrul dreptunghiului. Perimetrul paralelogramului. Perimetrul rombului. Perimetrul trapezului.
Unități de măsură pentru suprafețe. Transformări.
Unități de masură pentru suprafață. Metru pătrat. Multiplii și submultiplii metrului pătrat.
Aria unui dreptunghi
Deducerea formulei pentru arie dreptunghi. Exemplu de calcul pentru aria dreptunghiului.
Aria unui pătrat
Deducerea formulei pentru arie pătrat. Exemplu de calcul pentru aria pătratului.
Unități de măsură pentru volum. Transformări.
Unități de măsură pentru volum. Metru cub. Multiplii și submultiplii metrului cub.
Volumul cubului
Formula de calcul pentru volumul unui cub.
Volumul paralelipipedului dreptunghic
Formula de calcul pentrul volumul unui paralelipiped dreptunghic.
Unități de măsură pentru capacitate. Transformări.
Unități de măsură pentru capacitate. Litrul. Multiplii și submultiplii litrului.
Unități de măsură pentru masă. Transformări.
Unități de măsură pentru masă. Kilogramul. Transformări.
Unități de măsură pentru timp. Transformări.
Unități de măsură pentru timp. Ore,minute, secunde. Transformări.
Unități monetare
Unități monetare: lei, bani.
Aria paralelogramului
Formula pentru arie paralelogram. Înălțimea unui paralelogram. Aria paralelogramului folosind sinusul. Probleme cu aria unui paralelogram.
Aria rombului
Formula pentru arie romb. Aria rombului folosind sinusul. Probleme cu aria unui romb.
Aria trapezului
Formula pentru arie trapez. Înălțimea unui trapez. Probleme cu aria unui trapez.
Teorema paralelelor neechidistante
Împărțirea unui segment în părți proporționale cu numere date.
Teorema bisectoarei
Bisectoarea unui unghi determină pe latura opusă segmente proporționale cu celelalte două laturi.
Segmente proporționale
Raportul a două segmente. Segmente proporționale.
Latura, apotema și aria triunghiului echilateral înscris în cerc
Latura triunghiului echilateral în funcție de raza cercului circumscris. Apotema triunghiului echilateral în funcție de raza cercului circumscris. Formula pentru arie triunghi echilateral în funcție de raza cercului circumscris.
Latura, apotema și aria pătratului înscris în cerc
Latura pătratului în funcție de raza cercului circumscris. Apotema pătratului în funcție de raza cercului circumscris. Formula pentru arie pătrat în funcție de raza cercului circumscris.
Latura, apotema și aria hexagonului regulat înscris în cerc
Latura unui hexagon regulat în funcție de raza cercului circumscris. Formula pentru apotemă hexagon regulat în funcție de raza cercului circumscris. Formula pentru arie hexagon regulat în funcție de raza cercului circumscris. Perimetrul hexagonului.
Lungimea cercului. Lungimea unui arc de cerc
Lungimea cercului și lungimea unui arc de cerc.
Noţiuni de termochimie, partea I
Tipuri de energie. Termodinamică – definiţie. Energie potenţială. Energie gravitaţională. Lucru mecanic. Căldură. Energie internă. Variaţia energiei interne într-un sistem termodinamic.
Noţiuni de termochimie, partea II
Reacţii endoterme. Reacţii exoterme. Efecte termice: degajare de căldură, absorbţie de căldură. Căldura de reacţie. Condiţii standard de determinare a căldurii de reacţie.
Entalpia
Energie cinetică. Energie potenţială. Energie internă. Funcţii de stare şi funcţii de proces. Variabile de stare. Mărimi de stare extensive şi intensive. Transfer de energie internă. Entalpia. Semnificaţia relaţiei de definire a entalpiei. Variaţia entalpiei. Calorimetrie.
Legea lui Hess. Entalpia de formare standard.
Termochimie. Variaţia entalpiei în reacţiile endoterme. Variaţia entalpiei în reacţiile exoterme. Legea aditivităţii căldurilor de reacţie – Legea lui Hess. Condiţii standard de reacţie. Entalpia molară de formare standard.
Căldura de combustie
Combustie. Tipuri de combustibili. Entalpia de combustie standard. Ardere completă şi ardere incompletă. Căldura de combustie. Puterea calorică. Condiţii normale pentru măsurarea puterii calorice. Putere calorică inferioară şi putere calorică superioară.
Aplicaţii
Căldura specifică, c. Căldura specifică molară. Exemple de calcul pentru capitolul termochimie.
Viteza de reacţie
Cinetica chimică – definiţie. Viteza medie de reacţie. Variaţia concentraţiei reactanţilor şi a produşilor de reacţie în timp. Exemplu de calcul pentru viteza medie de reacţie. Clasificarea reacţiilor chimice în funcţie de viteza de reacţie. Reacţii rapide. Reacţii cu viteză moderată. Reacţii lente. Măsurarea vitezei de reacţie.
Energia de activare. Teoria complexului activat.
Redistribuirea legăturilor chimice în timpul unei reacţii. Ciocniri eficace. Ciocniri ineficace. Energie de activare. Stare de tranziţie sau complex activat. Energia potenţială a complexului activat. Reprezentarea grafică a energiei de activare pentru o reacţie endotermă şi pentru o reacţie exotermă. Energia de activare a reacţiei directe şi energia de activare a reacţiei inverse. Teoria complexului activat. Condiţia geometrică şi condiţia energetică pentru ciocniri eficace.
Legea vitezei de reacţie
Viteza de reacţie. Variaţia vitezei de reacţie în funcţie de concentraţia reactanţilor şi în funcţie de concentraţia produşilor. Legea vitezei de reacţie. Expresia matematică a vitezei de reacţie. Constanta vitezei de reacţie. Ordine parţiale de reacţie. Ordin total de reacţie. Ordine parţiale de reacţie vs coeficienţi stoechiometrici.
Influenţa suprafeţei de contact şi a temperaturii asupra vitezei de reacţie
Factorii care influenţează viteza de reacţie. Influenţa suprafeţei de contact asupra vitezei de reacţie. Influenţa temperaturii asupra vitezei de reacţie. Dependenţa constantei de viteză de temperatură. Relaţia lui Arrhenius. Semnificaţia matematică a elementelor din relaţia lui Arrhenius. Determinarea energiei de activare. Metoda grafică de determinare a energiei de activare.
Influenţa catalizatorilor asupra vitezei de reacţie
Catalizatori – definiţie şi mod de funcţionare. Reprezentarea grafică a energiei de activare pentru o reacţie necatalizată şi o reacţie catalizată. Etapa determinantă de viteză. Reacţii catalitice. Proprietăţile catalizatorilor - activitatea catalitică, selectivitatea. Promotorii şi otrăvurile. Tipuri de reacţii catalitice –reacţii omogene, eterogene şi enzimatice. Suport catalitic. Inhibitori.
Aplicaţii
Timp de înjumătăţire. Unităţi de măsură pentru constanta de viteză. Exemple de calcul.
Paralelipipedul dreptunghic
Aria paralelipipedului și volumul paralelipipedului. Deducerea formulelor de calcul pentru arie paralelipiped și volum paralelipiped dreptunghic. Aria laterală a paralelipipedului. Aria totală a paralelipipedului. Volumul unui paralelipiped dreptunghic.
Numere naturale scrise în formă arabă și romană
Scrierea unui număr cu cifre arabe sau cifre romane. Reguli de scriere folosind cifrele romane
Cubul
Aria cubului și volumul cubului. Deducerea formulelor de calcul pentru arie cub și volum cub. Aria laterală a cubului. Aria totală a cubului. Volumul cubului.
Aproximarea și rotunjirea numerelor naturale
Aproximarea prin lipsă și prin adaos, rotunjirea numerelor naturale
Operații cu numere naturale. Adunarea
Adunarea numerelor naturale. Proprietățiile adunării
Operații cu numere naturale. Scăderea
Scăderea numerelor naturale.
Adunarea numerelor naturale. Suma lui Gauss
Modalități de determinare a formulei sumei lui Gauss.
Operații cu numere naturale. Înmulțirea
Înmulțirea numerelor naturale. Proprietățiile înmulțirii.
Înmulțirea numerelor naturale. Factor comun
Definiția factorului comun. Scoaterea factorului comun
Operații cu numere naturale. Împărțirea
Împărțirea numerelor naturale. Împărțirea exactă (cu rest zero) a două numere naturale. Împărțirea cu rest diferit de zero a două numere naturale. Enunțarea teoremei împărțirii cu rest.
Divizor. Multiplu. Noțiuni introductive
Divizori ai unui număr natural. Multiplii unui număr natural.
Criterii de divizibilitate cu 2, 5 și 10
Enunțarea criteriilor de divizibilitate. Criteriul de divizibilitate cu 2. Criteriul de divizibilitate cu 5. Criteriul de divizibilitate cu 10.
Ecuații în mulțimea numerelor naturale
Exprimarea ecuațiilor cu ajutorul balanțelor. Rezolvarea principalelor tipuri de ecuații date în mulțimea numerelor naturale
Inecuații în mulțimea numerelor naturale
Rezolvarea inecuațiilor în mulțimea numerelor naturale
Media aritmetică a două sau mai multe numere naturale
Formula de calcul pentru medie aritmetică. Media aritmetică a numerelor naturale.
Reprezentarea numerelor raționale pozitive pe axa numerelor
Reprezentarea fracțiilor subunitare, echiunitare și supraunitare pe axa numerelor
Adunarea și scăderea fracțiilor cu același numitor
Operații cu numere raționale pozitive reprezentate prin fracții care au același numitor. Adunarea fracțiilor cu același numitor. Scăderea fracțiilor cu același numitor.
Aflarea unei fracții dintr-un număr
Modalități de calcul pentru determinarea unei fracții dintr-un număr natural sau pentru determinarea unei fracții dintr-o altă fracție (înmulțirea a două fracții)
Numere (fracții) zecimale
Numere zecimale. Citirea numerelor zecimale. Partea întreagă, partea zecimală (fracționară).
Puteri cu exponent întreg
Puterea cu exponent întreg a unui număr real. Proprietățile puterilor cu exponent întreg. Inversul unui număr. Calculul puterilor cu exponent negativ.
Logaritmi
Noțiunea de logaritm, exemple de logaritmi. Condițiile de existență a logaritmilor.
Puteri cu exponent rațional
Puteri cu exponent rațional. Proprietățile puterilor cu exponent rațional. Scrierea puterilor cu exponent rațional cu ajutorul radicalilor. Ordonarea puterilor, compararea puterilor cu exponent rațional.
Proprietățile logaritmilor
Propritățile logaritmilor: logaritmul produsului, logaritmul raportului, logaritmul unei puteri. Formula pentru schimbarea bazei logaritmului și alte formule logaritmice. Operații cu logaritmi.
Radicali de ordin n
Radicalul de ordin n dintr-un număr real pozitiv. Radicalul de ordin impar dintr-un număr negativ. Proprietățile radicalilor de ordin superior: produsul radicalilor, câtul a doi radicali, puterea unui radical, amplificarea, simplificarea radicalilor, compunerea radicalilor, scoaterea factorilor de sub radical și introducerea factorilor sub radical.
Compararea radicalilor
Aducerea radicalilor la același ordin. Compararea radicalilor de ordin n. Exerciții de ordonare a radicalilor de ordin superior.
Ecuații de gradul I
Forma generală e ecuațiilor de gradul I. Modalitatea teoretică de rezolvare a unei ecuații de gradul întâi. Interpretarea geometrică pentru ecuația de gradul I. Ecuații cu parametru real- exerciții.
Inecuații de gradul I
Forma generală a inecuațiilor de gradul I cu o necunoscută. Modalitatea teoretică de rezolvare a unei inecuații de gradul întâi. Ecuații cu modul, explicitarea modulului.
Sisteme formate dintr-o ecuație de gradul I și o ecuație de gradul II
Rezolvarea unor tipuri de sisteme de ecuații cu coeficienți reali: sisteme formate dintr-o ecuație de gradul I și o ecuație de gradul II. Interpretarea geometrică a acestora
Sisteme de ecuații omogene
Ecuații omogene. Sisteme omogene, algoritmul de rezolvare.
Sisteme de ecuații simetrice
Ecuații simetrice. Sisteme de ecuații simetrice. Algoritmul de rezolvare a sistemelor simetrice. Sistem simetric fundamental.
Funcția de gradul II
Funcția de gradul al doilea: definiția funcției de gradul II. Noțiuni introductive. Probleme care conduc la funcția de gradul doi. Exemple de funcții de gradul doi. Graficul unei funcții de gradul II.
Semnul funcției de gradul II
Semnul funcției de gradul al doilea. Convexitate. Concavitate. Funcție convexă, funcție concavă. Graficul funcției de gradul doi (convex, concav). Poziții relative ale graficului funcției de gradul II.
Monotonia funcției de gradul II
Funcția de gradul II, forma canonică a funcției de gradul al doilea. Punct de minim, punct de maxim. Vârf parabolă- coordonate. Tabel de variație, monotonia funcției de gradul al doilea.
Ecuații de gradul al doilea
Recapitulare ecuații de gradul II cu rădăcini reale. Modalități de rezolvare. Ecuația de gradul al doilea: formarea ecuației când se cunosc rădăcinile (folosind suma și produsul rădăcinilor).
Operații cu radicali. Raționalizarea numitorului
Operații cu radicali de ordin n. Înmulțirea radicalilor, împarțirea radicalilor, ridicarea la putere. Scoaterea și introducerea factorilor sub radical. Amplificarea și simplificarea radicalilor. Compunerea radicalilor. Raționalizarea numitorului. Perechi de expresii conjugate.
Inecuații de gradul al doilea
Inecuații de gradul II: forma generală, modalități de rezolvare. Exemple de inecuații de gradul doi.
Inecuații de gradul al doilea ce conțin modul
Inecuații de gradul II ce conțin modul. Explicitarea modulului unei inecuații de gradul doi.
Sisteme de inecuații de gradul al doilea
Sisteme formate din inecuații de gradul II și inecuații de gradul I, sau sisteme ce conțin doar inecuații de gradul II.
Rezolvarea ecuațiilor de gradul II în mulțimea numerelor complexe
Ecuații de gradul al doilea cu soluții complexe. Formarea ecuației de gradul doi când se cunosc soluțiile complexe. Descompunerea trinomului de gradul doi în factori liniari.
Mulțimea numerelor complexe
Noțiunea de număr complex. Mulțimea numerelor complexe.
Numere complexe scrise sub formă algebrică
Forma algebrică a numerelor complexe. Partea reală a unui număr complex. Partea imaginară a unui număr complex. Definirea operațiilor algebrice cu numere complexe. Puterile numărului complex i. Numere complexe conjugate. Determinarea raportului dintre două numere complexe. Modulul unui număr complex. Conjugatul unui număr complex.
Funcții trigonometrice- coordonate în plan
Funcții trigonometrice- coordonatele punctelor situate în cele patru cadrane ale cercului trigonometric.
Operația de logaritmare, calcule cu logaritmi
Logaritmarea unei expresii, calcule cu logaritmi. Restrângerea unor expresii folosind proprietățile logaritmilor.
Forma trigonometrică a numerelor complexe
Numere complexe exprimate trigonometric. Coordonate polare în plan. Raza polară. Argumentul unui număr complex. Pentru a determina argumentul redus al unui număr complex vom ține cont de cadranul în care se află imaginea geometrică a numărului complex.
Ecuații iraționale
Ecuații iraționale- ecuații ce conțin necunoscuta sub radical; metode de rezolvare a ecuațiilor iraționale
Înmulțirea fracțiilor zecimale
Înmulțirea fracțiilor zecimale care au un număr finit de zecimale nenule
Ridicarea la putere cu exponent natural a fracțiilor zecimale
Ridicarea la putere a fracțiilor zecimale. Calculul unor puteri care au exponentul număr natural și baza număr zecimal. Reguli de calcul cu puteri.
Împărțirea fracțiilor zecimale
Împărțirea unui număr natural la o fracție zecimală finită, împărțirea unei fracții zecimale finite la un număr natural, împărțirea a două fracții zecimale finite
Ordinea efectuării operațiilor cu fracții zecimale
Operații cu fracții zecimale. Ordinea efectuării operațiilor cu fracții zecimale finite. Ordinea de efectuare a operațiilor din paranteze.
Media aritmetică a două sau mai multe fracții zecimale finite
Formula de calcul pentru medie aritmetică a fracțiilor zecimale finite. Interpretarea rezultatelor.
Operații cu intervale de numere reale
Reuniunea intervalelor. Intersecția intervalelor. Diferența dintre un interval și o mulțime finită.
Formula de trinom la pătrat
Determinarea formulei de calcul pentru pătratul unui trinom.
Cubul sumei și al diferenței
Determinarea formulelor de calcul pentru cubul sumei și cubul diferenței de două numere reale.
Adunarea și scăderea numerelor reale (2)
Adunarea și scăderea numerelor reale de forma 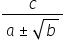
Înmulțirea și împărțirea numerelor reale (2)
Înmulțirea și împărțirea numerelor reale de forma 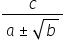
Ridicarea la putere a rapoartelor de numere reale
Ridicarea la putere cu exponent întreg a unor rapoarte de numere reale. Reguli de calcul cu puteri
Inecuații cu numere zecimale
Rezolvarea inecuațiilor cu numere zecimale. Tipuri de inecuații
Probleme care se rezolvă cu ajutorul ecuațiilor (numere zecimale)
Rezolvarea unor probleme folosind ecuații matematice
Sisteme de ecuații- metoda grafică
Rezolvarea unui sistem de două ecuații cu două necunoscute prin metoda grafică.
Sisteme de ecuații- metoda substituției
Rezolvarea unui sistem de două ecuații cu două necunoscute prin metoda substituției.
Sisteme de ecuații- metoda reducerii
Rezolvarea unui sistem de două ecuații cu două necunoscute prin metoda reducerii.
Probleme care se rezolvă cu ajutorul inecuațiilor (numere zecimale)
Rezolvarea unor probleme folosind inecuații matematice
Piramida triunghiulară regulată
Aria piramidei și volumul piramidei. Deducerea formulelor de calcul pentru arie piramidă triunghiulară regulată și volum piramidă triunghiulară regulată. Aria laterală a piramidei triunghiulare regulate. Aria totală a piramidei triunghiulare regulate. Volumul unei piramide triunghiulare regulate.
Piramida patrulateră regulată
Aria piramidei și volumul piramidei. Deducerea formulelor de calcul pentru arie piramidă patrulateră regulată și volum piramidă patrulateră regulată. Aria laterală a piramidei patrulatere regulate. Aria totală a piramidei patrulatere regulate. Volumul unei piramide patrulatere regulate.
Piramida hexagonală regulată
Aria piramidei și volumul piramidei. Deducerea formulelor de calcul pentru arie piramidă hexagonală regulată și volum piramidă hexagonală regulată. Aria laterală a piramidei hexagonale regulate. Aria totală a piramidei hexagonale regulate. Volumul unei piramide hexagonale regulate.
Trunchiul de piramidă regulată
Aria trunchiului de piramidă și volumul trunchiului de piramidă. Deducerea formulelor de calcul pentru arie trunchi de piramidă regulată și volum trunchi de piramidă regulată. Aria laterală a trunchiului de piramidă regulată. Aria totală a trunchiului de piramidă regulată. Volumul unui trunchi de piramidă regulată.
Cilindrul circular drept
Descrierea cilindrului circular drept. Elementele unui cilindru circular drept. Înălțimea cilindrului. Generatoarea unui cilindru. Secțiunea axială a cilindrului. Desfășurarea unui cilindru circular drept. Aria cilindrului și volumul cilindrului. Deducerea formulelor de calcul pentru arie cilindru circular și volum cilindru circular. Aria laterală a cilindrului circular drept. Aria totală a cilindrului circular drept. Volumul cilindrului circular drept.
Conul circular drept
Descrierea conului circular drept. Elementele unui con circular drept. Înălțimea conului. Generatoarea conului. Secțiunea axială a conului. Desfășurarea unui con circular drept. Aria conului și volumul conului. Deducerea formulelor de calcul pentru arie con circular și volum con circular. Aria laterală a conului circular drept. Aria totală a conului circular drept. Volumul conului circular drept.
Trunchiul de con circular drept
Descrierea trunchiului de con circular drept. Elementele unui trunchi de con circular drept. Înălțimea trunchiului de con. Generatoarea trunchiului de con. Secțiunea axială a trunchiului de con. Desfășurarea unui trunchi de con circular drept. Aria trunchiului de con și volumul trunchiului de con. Deducerea formulelor de calcul pentru arie trunchi de con și volum trunchi de con. Aria laterală a trunchiului de con circular drept. Aria totală a trunchiului de con circular drept. Volumul trunchiului de con circular drept.
Sfera
Descrierea unei sfere. Formulele de calcul pentru arie sferă și volum sferă. Probleme cu aria sferei și volumul sferei.
Reprezentarea geometrică a numerelor complexe
Imaginea geometrică a unui număr complex. Interpretarea geometrică a modulului unui număr complex. Interpretarea geometrică a sumei și a diferenței a două numere complexe. Interpretarea geometrică a numerelor complexe opuse și a numerelor complexe conjugate.
Funcții definite pe intervale
Trasarea graficului unor funcții care au ca domeniu de definiție un interval.
Determinarea dreptei și a planului
Modalități de a determina o dreaptă și un plan cu ajutorul unor axiome și a unor teoreme
Plane perpendiculare
Plane perpendiculare. Demonstrarea perpendicularității a două plane.
Noțiuni introductive de logică matematică
Noțiuni generale de logică matematică: propoziții, predicate, cuantificatori. Cuantificatorul existențial, cuantificatorul universal.Propoziție existențială, propoziție universală. Valoarea de adevăr a unei propoziții, mulțimea de adevăr a unui predicat. Propoziții adevărate, propoziții false. Principiile logicii matematice. Exerciții de stabilire a valorii de adevăr a unor propoziții.
Operații logice: negația
Negația propozițiilor, negația predicatelor. Complementara unei mulțimi. Negația propozițiilor care conțin cuantificatori. Valoarea de adevăr a negației unei propoziții. Mulțimea de adevăr a negației unui predicat.
Operații logice: conjuncția
Conjuncția propozițiilor, conjuncția predicatelor. Intersecția mulțimilor. Valoarea de adevăr a conjuncției a două propoziții. Mulțimea de adevăr a conjuncției predicatelor.
Operații logice: disjuncția
Disjuncția propozițiilor, disjuncția predicatelor. Reuniunea mulțimilor. Valoarea de adevăr a disjuncției a două propoziții. Mulțimea de adevăr a disjuncției predicatelor.
Operații logice: implicația
Implicația propozițiilor. Ipoteză, concluzie. Implicația predicatelor. Incluziunea mulțimilor. Valoarea de adevăr a implicației.
Operații logice: echivalența
Echivalența propozițiilor, echivalența predicatelor. Egalitatea mulțimilor. Valoarea de adevăr a echivalenței a două propoziții.
Formule de calcul propozițional. Legile lui De Morgan
Formulă de calcul propozițional. Formule echivalente. Legile lui De Morgan. Valoarea de adevăr a unei formule propoziționale. Noțiunea de tautologie.
Metoda inducției matematice
Inducție matematică. Etapele principiului inducției matematice (etapa de verificare, etapa de demonstrație). Demonstrația unei propoziții matematice folosind principiul inducției matematice.
Simbolul Sigma și calculul unor sume
Scrierea unor sume restrâns cu ajutorul simbolului Sigma. Proprietățile simbolului Sigma. Calculul unor sume, demonstație prin inducție matematică. Metoda coeficienților nedeterminați.
Metoda inducției matematice în demonstrarea unor inegalități
Demonstrarea unor inegalități prin inducție matematică.
Șiruri mărginite
Șir mărginit superior, șir mărginit inferior. Mărginirea șirurilor. Definiția șirurilor mărginite, exemple de șiruri mărginite.
Șiruri monotone
Șir crescător, șir descrescător, șir monoton. Definiția șirurilor monotone. Metode prin care se poate studia monotonia șirurilor. Exemple de șiruri monotone.
Progresii geometrice- noțiuni introductive
Noțiunea de progresie geometrică. Proprietățile progresiei geometrice. Exemple de progresii geometrice.
Proprietățile progresiei geometrice
Termenul general al unei progresii geometrice în funcție de primul termen și de rația progresiei. Condiția ca n numere să fie în progresie geometrică. Suma primilor n termeni ai unei progresii geometrice.
Funcții mărginite
Imaginea unei funcții, noțiunea de funcție mărginită. Graficul unei funcții mărginite. Mărginirea unei funcții numerice.
Funcții pare, funcții impare
Funcție pară, funcție impară. Exemple de funcții pare, funcții impare. Graficul unei funcții pare. Graficul unei funcții impare. Proprietăți ale graficelor. Paritatea funcțiilor - exerciții.
Funcții periodice
Noțiunea de funcție periodică, noțiunea de perioadă, perioadă principală. Exemple de funcții periodice. Proprietăți ale funcțiilor periodice. Graficul unei funcții periodice - proprietate. Periodicitatea funcțiilor - exerciții.
Monotonia funcțiilor numerice
Funcție crescătoare, funcție descrescătoare, funcție monotonă. Exemple de funcții monotone. Modalități de a studia monotonia funcțiilor. Intervale de monotonie. Exerciții de stabilire a monotoniei funcțiilor.
Compunerea funcțiilor
Compunerea funcțiilor. Proprietăți ale compunerii funcțiilor. Exerciții- funcții compuse.
Funcții numerice- noțiuni introductive
Noțiunea de funcție numerică, modalități de definire a unei funcții numerice și exemple de funcții. Graficul unei funcții. Reprezentarea grafică a unei funcții numerice.
Operații cu funcții numerice
Operații cu funcții: suma funcțiilor, produsul funcțiilor, câtul funcțiilor.
Semnul funcției de gradul I
Semnul funcției de gradul I. Exerciții de stabilire a semnului funcției de gradul I. Semnul unor expresii algebrice. Rezolvarea unor ecuații cu modul și inecuații cu modul, folosind semnul funcției de gradul I.
Relațiile lui Viete. Natura și semnele rădăcinilor ecuației de gradul II
Legătura dintre rădăcinile reale ale ecuației de gradul al doilea și coeficienții acesteia. Formarea ecuației de gradul al doilea când se cunosc rădăcinile. Natura rădăcinilor și semnele rădăcinilor ecuației de gradul al doilea.
Descompunerea trinomului de gradul II
Descompunerea unui trinom de gradul al doilea în factori liniari. Simplificarea unor expresii algebrice.
Vectori
Direcția unei drepte. Segmente cu aceeași direcție. Segmente orientate. Segmente echipolente. Noțiunea de vector. Vector nul. Vector unitate. Vectori egali. Vectori opuși.
Adunarea vectorilor
Adunarea vectorilor: regula paralelogramului, regula triunghiului, regula poligonului. Proprietățile operației de adunare a vectorilor.
Înmulțirea vectorilor cu scalari
Înmulțirea unui vector cu un scalar. Proprietăți ale înmulțirii vectorilor cu scalari.
Descompunerea unui vector într-un reper cartezian
Noțiunea de versor. Descompunerea unui vector după doi vectori dați. Coordonatele unui vector. Înmulțirea unui vector cu un scalar. Suma vectorilor. Coliniaritatea vectorilor. Vectori egali. Formula de calcul pentru lungimea unui vector exprimat cu ajutorul versorilor. Modulul unui vector. Expresia analitică a unui vector.
Vectori în reper cartezian
Vectori exprimați cu ajutorul versorilor: coordonatele unui vector, modulul unui vector.
Scăderea vectorilor
Diferența vectorilor.
Vectori coliniari
Vectori coliniari, condiția de coliniaritate a doi vectori.
Echilibre acido-bazice. Tăria acizilor. Exponentul de aciditate.
Protonul și ionul de hidrogen. Ionul hidroniu și ionul hidroxil. Teoria protolitică Brønsted-Lowry. Cuplu acid-bază conjugată. Echilibru acido-bazic. Constanta de aciditate. Disocierea în apă a acizilor tari. Disocierea în apă a acizilor slabi. Exemple de acizi tari. Exemple de acizi slabi.
Tăria bazelor. Constanta de bazicitate și exponentul de bazicitate.
Disocierea bazelor tari în apă. Disocierea bazelor slabe în apă. Exemple de baze tari și baze slabe. Constanta de bazicitate. Exponentul de bazicitate. Apa - substanță amfoteră (amfolit acido-bazic). Produsul ionic al apei.
pH-ul soluțiilor apoase de acizi
Definiție pH. Produsul ionic al apei. pH și pOH. Calculul concentrației ionilor hidroniu pentru soluțiile de acizi tari și pentru soluțiile de acizi slabi. Calculul pH-ului pentru soluțiile de acizi tari și pentru soluțiile de acizi slabi. Exemplu de calcul pH pentru o soluție de acid tare. Exemplu de calcul pH pentru o soluție de acid slab.
pH-ul soluțiilor apoase de baze
Calculul concentrației ionilor hidroxil din soluțiile de baze tari și din soluțiile de baze slabe. Calculul concentrației ionilor hidroniu din soluțiile de baze tari și din soluțiile de baze slabe. Calculul pH-ului soluțiilor de baze tari și al soluțiilor de baze slabe. Exemplu de calcul pH pentru o soluție de bază tare. Exemplu de calcul pH pentru o soluție de bază slabă (o soluție de amoniac).
Reacția de neutralizare în soluții apoase
Reacția de neutralizare - definiție. Neutralizarea unui acid tare cu o bază tare. Ioni spectatori. Căldura molară de neutralizare. Formarea sărurilor prin neutralizarea unui acid tare cu o bază tare. Reacția dintre un acid slab și o bază tare. Reacția dintre un acid tare și o bază slabă.
Titrări acido-bazice
Reacția de neutralizare. Titrare acido-bazică. Punct de echivalență. Indicatori acido-bazici. Domeniu de viraj. Exemple de indicatori acido-bazici: metiloranj, turnesol, fenolftaleină. Biuretă. Exemplu de calcul: aflarea concentrației unei soluții de acid clorhidric prin titrare acido-bazică cu o soluție de hidroxid de sodiu de concentrație cunoscută.
Hidroliza sărurilor
Sărurile - compuși ionici. Comportamentul anionilor în apă. Comportamentul cationilor în apă. Reacția de hidroliză. Săruri care formează soluții neutre (săruri provenite de la acizi tari și baze tari). Săruri care formează soluții acide (săruri provenite de la acizi tari și baze slabe). Săruri care formează soluții bazice (săruri provenite de la acizi slabi și baze tari). Săruri provenite de la acizi slabi și baze slabe. Hidroliza azotatului de sodiu (NaNO3), hidroliza clorurii de amoniu (NH4Cl), hidroliza sulfurii acide de sodiu (NaHS), hidroliza cianurii de amoniu (NH4CN). Aplicații; calculul pH-ului unei soluții de sare.
Șiruri
Șiruri, notații, moduri de a defini un șir. Șir definit descriptiv, șir definit printr-o regulă de calcul, șir definit printr-o relație de recurență. Termenii unui șir. Rangul unui termen. Exemple de șiruri.
Progresii aritmetice- noțiuni introductive
Noțiunea de progresie aritmetică, rația progresiei, proprietățile progresiei aritmetice. Exemple de progresii aritmetice.
Proprietățile progresiei aritmetice
Termenul general al unei progresii aritmetice în funcție de primul termen și de rație. Proprietățile progresiei aritmetice. Condiția ca n numere sa fie în progresie aritmetică. Suma primilor n termeni ai unei progresii aritmetice.
Funcția de gradul I
Funcția de gradul întâi. Graficul funcției de gradul I, intersecția cu axele. Monotonia unei funcții de gradul I. Reprezentarea grafică a funcției de gradul I, funcții definite pe ramuri.
Vectorul de poziție al unui punct
Vector de poziție al unui punct. Vectorul de poziție al punctului care împarte un segment într-un raport dat. Vector de poziție al mijlocului unui segment.
Vectorul de poziție al centrului de greutate al unui triunghi
Vector de poziție al centrului de greutate al unui triunghi ABC, exprimat cu ajutorul vectorilor de poziție ai punctelor A, B, C.
Teorema lui Menelaus
Condiția de coliniaritate a trei puncte. Teorema lui Menelaus și reciproca.
Teorema lui Ceva
Concurența unor linii într-un triunghi. Teorema lui Ceva. Reciproca teoremei lui Ceva.
Măsurarea unghiurilor
Măsurarea unghiurilor în grade sexagesimale și radiani. Transformarea gradelor în radiani. Tranformarea radianilor în grade.
Cercul trigonometric
Cerc trigonometric (cerc unitate). Exprimarea unghiurilor uzuale în grade și radiani și scrierea coordonatelor punctelor de pe cerc corespunzătoare.
Operații cu numere complexe scrise sub formă algebrică
Adunarea numerelor complexe. Scăderea numerelor complexe. Modulul unui număr complex. Conjugatul unui număr complex. Înmulțirea numerelor complexe. Raportul a două numere complexe. Egalitatea a două numere complexe.
Funcția cosinus
Funcția cosinus. Proprietăți: semnul funcției cosinus, periodicitate, paritate, monotonie. Graficul funcției cosinus.
Funcția tangentă
Funcția tangentă. Proprietăți: semnul funcției tangentă, periodicitate, paritate, monotonie. Graficul funcției tangentă.
Funcția cotangentă
Funcția cotangentă. Proprietăți: semnul funcției cotangentă, periodicitate, paritate, monotonie. Graficul funcției cotangentă.
Relațiile între funcțiile trigonometrice ale unui unghi
Formula fundamentală a trigonometriei. Formule trigonometrice pentru unghiuri complementare. Relații între funcții trigonometrice.
Reducerea la primul cadran
Calculul funcțiilor trigonometrice folosind formule de reducere la primul cadran. Trecerea din cadranul II în cadranul I. Trecerea din cadranul III în cadranul I. Trecerea din cadranul IV în cadranul I.
Formule trigonometrice ale sumei și diferenței a două unghiuri
Formule trigonometrice pentru suma și diferența a două unghiuri
Formule trigonometrice pentru argumentul dublu și triplu
Formulele trigonometrice ale argumentului dublu și triplu.
Transformarea sumelor în produse
Transformarea sumelor în produse
Transformarea produselor în sume
Transformarea produselor în sume
Produsul scalar a doi vectori
Produsul scalar a doi vectori. Proprietățile produsului scalar. Produs scalar: expresia analitică. Unghiul a doi vectori. Modulul unui vector.
Teorema cosinusului
Aplicații ale produsului scalar: teorema cosinusului.
Teorema medianei
Aplicații ale produsului scalar: teorema medianei.
Teorema sinusurilor
Teorema sinusurilor.
Rezolvarea triunghiurilor oarecare
Rezolvarea triunghiurilor oarecare (folosind teorema cosinusului, teorema sinusurilor).
Aria triunghiului- formula lui Heron
Aria triunghiului oarecare folosind formula lui Heron.
Razei cercului circumscris și raza cercului înscris în triunghi
Formulele de calcul pentru raza cercului circumscris și raza cercului înscris în triunghi.
Funcția sinus
Funcția sinus. Proprietăți: semnul funcției sinus, periodicitate, paritate, monotonie. Graficul funcției sinus.
Operații cu permutări
Compunerea permutărilor de grad n.Proprietăți ale compunerii permutărilor de grad n. puterea unei permutări de grad n.Proprietăți ale transpozițiilor.
Noțiunea de permutare
Noțiunea de permutare, noțiunea de permutare de grad n, exemple, permutări de grad n particulare
Inversiunile unei permutări. Semnul unei permutări
Inversiunile unei permutări. Semnul unei permutări.Permutări pare. Permutări impare
Înmulțirea numerelor complexe scrise sub formă trigonometrică
Operații cu numere complexe exprimate trigonometric: înmulțirea numerelor complexe. Modulul produsului. Argumentul produsului.
Ridicarea la putere a numerelor complexe sub formă trigonometrică
Operații cu numere complexe exprimate trigonometric: ridicarea la putere a unui număr complex. Formula lui Moivre. Modulul puterii. Argumentul puterii.
Împărțirea numerelor complexe sub formă trigonometrică
Operații cu numere complexe exprimate trigonometric: împărțirea numerelor complexe. Modulul câtului. Argumentul câtului.
Rădăcinile de ordinul n ale unui număr complex
Rădăcina de ordin n dintr-un număr complex. Rădăcinile de ordin n ale unității.
Ecuații binome
Rezolvarea ecuațiilor binome.
Proprietăți ale funcțiilor: injectivitate
Funcții injective, noțiunea de funcție injectivă. Modalități de a studia injectivitatea unei funcții.
Proprietăți ale funcțiilor: surjectivitate
Funcții surjective, noțiunea de funcție surjectivă. Modalități de a studia surjectivitatea unei funcții.
Proprietăți ale funcțiilor: bijectivitate
Funcții bijective, noțiunea de funcție bijectivă. Modalitați de a studia bijectivitatea unei funcții.
Funcții inversabile
Funcții inverse. Inversa unei funcții. Condiția necesară și suficientă ca o funcție să fie inversabilă.
Funcția putere cu exponent natural
Funcția putere cu exponent natural și proprietățile acesteia: paritate, monotonie, semnul funcției. Graficul funcției putere cu exponent natural.
Funcția radical de ordin n
Funcția radical de ordin n și proprietățile acesteia. Graficul funcției radical de ordin n.
Funcția exponențială
Noțiunea de creștere exponențială, descreștere exponențială. Funcția exponențială și proprietățile acesteia. Grafice de funcții exponențiale.
Funcția logaritmică
Funcția logaritmică și proprietățile acesteia. Graficul funcției logaritmice.
Ecuații exponențiale
Rezolvarea ecuațiilor exponențiale, diverse tipuri de ecuații exponențiale.
Inecuații exponențiale
Rezolvarea inecuațiilor exponențiale, diverse tipuri de inecuații exponențiale.
Ecuații logaritmice
Rezolvarea ecuațiilor logaritmice, diverse tipuri de ecuații logaritmice.
Inecuații logaritmice
Rezolvarea inecuațiilor logaritmice, diverse tipuri de inecuații logaritmice.
Funcția arcsinus
Funcția arcsinus: definiție, grafic, proprietăți, exemple.
Funcția arccosinus
Funcția arccosinus: definiție, grafic, proprietăți, exemple.
Funcția arctangentă
Funcția arctangentă: definiție, grafic, proprietăți, exemple.
Funcția arccotangentă
Funcția arccotangentă: definiție, grafic, proprietăți, exemple.
Tipuri de ecuații trigonometrice
Rezolvarea unor tipuri de ecuații trigonometrice:
- ecuații trigonometrice de forma: sinf(x)=sing(x), cosf(x)=cosg(x), tgf(x)=tgg(x), ctgf(x)=ctgg(x);
- ecuații trigonometrice care se reduc la ecuații algebrice;
- ecuații trigonometrice liniare în sin x și cos x.
Permutări
Noțiunea de permutare. Numărul permutărilor de grad n. Simbolul n! (n factorial). Exerciții cu permutări.
Aranjamente
Numărul de aranjamente de n elemente luate câte k. Exerciții cu aranjamente.
Combinări
Combinări. Numărul de combinări de n elemente luate câte k. Exerciții cu combinări.
Proprietăți ale combinărilor
Proprietăți ale combinărilor: formula combinărilor complementare, formula de recurență în calculul cu combinări. Numărul tuturor submulțimilor unei mulțimi cu n elemente. Calculul unor sume folosind proprietățile combinărilor.
Binomul lui Newton
Binomul lui Newton. Formula de calcul pentru suma Formula termenului general din dezvoltarea binomială.
Mulţimi mărginite
Noţiunile de minorant şi majorant al unei mulţimi. Mulţimi mărginite. Axioma lui Cantor.
Mulţimi nemărginite
Marginile unei mulţimi nemărginite. Dreapta reală încheiată. Operaţiile aritmetice în .
Vecinătăţile unui punct pe axa reală
Noţiunea de vecinătate a unui număr real. Punct de acumulare al unei mulţimi, punct izolat.
Şiruri convergente
Limita unui şir, definiţia cu vecinătăţi a limitei unui şir. Şir convergent. Şiruri care au limită. Şir divergent.
Proprietăţile limitei unui şir
Principalele proprietăţi ale şirurilor care au limită.
Criteriul de convergenţă cu epsilon
Criteriul de existenţă a limitei unui şir cu epsilon. Teorema de convergenţă cu epsilon în cazul limitei finite. Criteriul cu epsilon pentru limită infinită.
Operaţii cu şiruri convergente
Operaţii cu şiruri convergente: limita sumei a două şiruri convergente, limita produsului, limita câtului, limita unei puteri.
Criterii de existenţă a limitei unui şir: criteriul majorării
Criteriul majorării pentru şiruri convergente. Criteriul majorării pentru şiruri divergente.
Criterii de existenţă a limitei unui şir: criteriul cleştelui
Trecerea la limită în inegalitaţi. Criteriul cleştelui.
Proprietăţi ale şirurilor convergente la zero
Şiruri convergente la zero, proprietăţi. Operaţii cu şiruri convergente la zero.
Proprietatea lui Weierstrass
Proprietatea lui Weierstrass pentru studiul convergenţei şirurilor. Lema lui Cesaro.
Numărul e
Definiţia numărului real iraţional e. Şirul remarcabil
Limite remarcabile
Şiruri cu limita numărul e. Limite remarcabile.
Teorema Stolz-Cesaro
Metode de calcul a unor limite de şiruri: lema Stolz-Cesaro.
Limita unei funcții într-un punct
Noţiunea de limită a unei funcţii într-un punct. .
Limite laterale
Limitele la stânga şi la dreapta ale unei funcţii într-un punct. Limite laterale. Criteriul de existenţă a limitei unei funcţii într-un punct folosind limitele laterale.
Criterii de existenţă a limitei unei funcţii: criteriul majorării
Criterii de existenţă a limitei unei funcţii într-un punct: criteriul majorării pentru limite finite şi criteriul majorării pentru limite infinite.
Trecerea la limită în inegalităţi. Criteriul cleştelui (pentru limite de funcţii)
Trecerea la limită în inegalităţi. Criteriul cleştelui (pentru limite de funcţii)
Limitele unor funcţii elementare
Limita funcţiei raţionale în caz de nedeterminare 0/0.
Limitele funcţiilor elementare
Limita funcției raționale. Limita funcţiei radical. Limita funcţiei exponenţiale. Limita funcţiei logaritmice.
Limitele funcţiilor trigonometrice directe
Limitele funcţiilor trigonometrice directe: sinus, cosinus, tangentă, cotangentă.
Limitele funcţiilor trigonometrice inverse
Limitele funcţiilor trigonometrice inverse: arcsinus, arccosinus, arctangentă, arccotangentă.
Operaţii cu limite de funcţii
Operaţii cu limite de funcţii: adunarea, înmulţirea, câtul, ridicarea la putere.
Funcţie continuă într-un punct
Definiţia unei funcţii continue într-un punct. Punct de continuitate. Puncte de discontinuitate.
Continuitatea laterală
Funcţie continuă la stânga într-un punct, funcţie continuă la dreapta.
Puncte de discontinuitate
Punct de discontinuitate de prima speţă, punct de discontinuitate de a doua speţă.
Continuitatea pe o mulţime
Funcţii continue pe o mulţime.
Operaţii cu funcţii continue
Suma, produsul, câtul a două funcţii continue. Puteri de funcţii continue.
Proprietăţi ale funcţiilor continue pe un interval: proprietatea lui Darboux
Funcţii cu proprietatea lui Darboux. Proprietăţi ale funcţiilor continue pe un interval. Teorema Cauchy-Weierstrass-Bolzano.
Funcţii continue pe un interval: existenţa soluţiilor unei ecuaţii
Proprietăţi ale funcţiilor continue pe un interval: existenţa soluţiilor unei ecuaţii.
Funcţii continue pe un interval: stabilirea semnului
Stabilirea semnului unei funcţii continue pe un interval.
Mărginirea funcţiilor continue pe un interval închis
Proprietăţi de mărginire ale funcţiilor continue pe un interval închis. Teorema lui Weierstrass.
Derivata unei funcţii într-un punct
Noţiunea de derivată a unei funcţii într-un punct. Definiţia derivatei. Funcţii derivabile.
Continuitatea funcţiilor derivabile
Legătura dintre funcţiile continue şi funcţiile derivabile. Condiţia necesară pentru derivabilitatea unei funcţii într-un punct.
Derivate laterale
Derivata la stânga şi derivata la dreapta a unei funcţii într-un punct. Existenţa derivatei unei funcţii într-un punct folosind derivatele laterale.
Puncte remarcabile ale graficului unei funcţii: puncte de întoarcere
Puncte remarcabile pentru graficul unei funcţii: puncte de întoarcere.
Puncte remarcabile ale graficului unei funcţii: puncte unghiulare
Puncte remarcabile pentru graficul unei funcţii: puncte unghiulare.
Puncte remarcabile ale graficului unei funcţii: puncte de inflexiune
Puncte remarcabile pentru graficul unei funcţii: puncte de inflexiune.
Derivatele unor funcţii elementare
Derivatele unor funcţii elementare: funcţia constantă, funcţia putere, funcţia radical de ordin n, funcţia logaritmică, funcţia exponenţială.
Derivatele funcţiilor trigonometrice sinus şi cosinus
Derivatele funcţiilor trigonometrice sinus şi cosinus.
Operaţii cu funcţii derivabile (1)
Operaţii cu funcţii derivabile. Derivata sumei, derivata produsului, derivata câtului a două funcţii.
Operaţii cu funcţii derivabile (2)
Operaţii cu funcţii derivabile. Derivarea funcţiilor compuse.
Operaţii cu funcţii derivabile (3)
Operaţii cu funcţii derivabile. Derivarea funcţiei inverse.
Derivatele funcţiilor trigonometrice inverse
Derivatele funcţiilor trigonometrice inverse: funcţia arcsinus, arccosinus, arctangentă, arccotangentă.
Derivate de ordin superior
Derivate de ordin superior: derivata de ordinul II. Definiţia derivatei a doua.
Puncte de extrem ale unei funcţii
Puncte de extrem ale unei funcţii: punct de maxim local, punct de minim local, punct de maxim absolut, punct de minim absolut.
Teorema lui Fermat
Teorema lui Fermat.
Teorema lui Rolle
Teorema lui Rolle
Teorema lui Lagrange
Teorema lui Lagrange
Consecinţe ale teoremei lui Lagrange
Consecinţe ale teoremei lui Lagrange. Funcţii cu derivata nulă. Funcţii cu derivate egale.
Regulile lui l'Hospital
Regulile lui l'Hospital. Rezolvarea unor cazuri de nedeterminare în calculul limitelor de funcţii cu ajutorul derivatelor.
Rolul derivatei întâi în studiul funcţiilor
Rolul derivatei întâi în studiul funcţiilor. Determinarea intervalelor de monotonie ale unei funcţii. Determinarea punctelor de extrem.
Rolul derivatei a doua în studiul funcţiilor
Rolul derivatei a doua în studiul funcţiilor. Determinarea intervalelor de convexitate şi concavitate. Determinarea punctelor de inflexiune.
Asimptote orizontale
Noţiunea de asimptotă orizontală.
Asimptote oblice
Noţiunea de asimptotă oblică.
Asimptote verticale
Noţiunea de asimptotă verticală.
Primitive. Integrala nedefinită a unei funcţii
Noţiunea de funcţie primitivă. Primitivele unei funcţii. Integrala nedefinită a unei funcţii.
Existenţa primitivelor
Condiţii ca o funcţie să admită primitive.
Proprietăţi ale integralei nedefinite
Proprietăţi ale integralei nedefinite.
Primitive uzuale
Tabelul integralelor nedefinite deduse din derivatele funcţiilor elementare.
Metoda integrării prin părţi
Metode de calcul ale primitivelor: formula de integrare prin părţi.
Metoda integrării prin substituţie (schimbare de variabilă)
Metode de calcul ale primitivelor: formula schimbării de variabilă
Diviziuni ale unui interval. Sume Riemann
Definirea noţiunilor de: diviziune a unui interval [a,b], norma unei diviziuni, suma Riemann.
Integrala definită
Definiţia integrabilităţii unei funcţii pe un interval [a,b]. Noţiunea de funcţie integrabilă Riemann. Integrala definită.
Integrabilitatea funcţiilor continue
Integrabilitatea funcţiilor continue. Condiţii ca o funcţie să fie integrabilă.Teorema lui Lebesgue.
Formula lui Leibniz-Newton
Metode de calcul pentru integrala definită. Formula lui Leibniz-Newton.
Proprietăţi ale integralei definite
Proprietăţi ale integralei definite: proprietatea de liniaritate, proprietatea de aditivitate la interval, pozitivitatea integralei, monotonia integralei, inegalitatea mediei, modulul integralei.
Metoda integrării prin părţi
Metode de calcul pentru integrale definite, metoda integrării prin părţi.
Integrarea prin schimbare de variabilă (1)
Metode de calcul pentru integrale definite: metoda integrării prin substituţie. Prima metodă de schimbare de variabilă.
Integrarea prin schimbare de variabilă (2)
Metode de calcul pentru integrale definite: metoda integrării prin substituţie. A doua metodă de schimbare de variabilă.
Teorema de medie
Teorema de medie, interpretare geometrică.
Aria unei suprafeţe plane
Aria unui subgrafic. Aria suprafeţelor plane cuprinse între două curbe.
Volumul corpurilor de rotaţie
Volumul corpurilor de rotaţie.
Lege de compoziţie internă
Lege de compoziţie pe o mulţime.
Parte stabilă
Noţiunea de parte stabilă.
Proprietăţi ale legilor de compoziţie (1)
Proprietăţi ale legilor de compoziţie: proprietatea de comutativitate şi proprietatea de asociativitate.
Proprietăţi ale legilor de compoziţie (2)
Proprietăţi ale legilor de compoziţie: element neutru, elemente simetrizabile.
Monoizi
Noţiunea de monoid, monoid comutativ.
Grupuri
Definiţia grupului. Grup abelian. Exemple de grupuri. Grup finit. Ordinul unui grup.
Reguli de calcul într-un grup
Reguli de calcul într-un grup: puterea unui element, legi de simplificare.
Morfisme de grupuri
Morfism de grupuri. Izomorfism de grupuri. Grupuri izomorfe. Endomorfism al unui grup. Automorfism al unui grup.
Subgrupuri
Definiţia noţiunii de subgrup.
Inele
Noţiunea de inel. Inel comutativ. Exemple de inele.
Reguli de calcul într-un inel
Divizori ai lui zero într-un inel. Noţiunea de inel integru (domeniu de integritate). Regula semnelor într-un inel. Legi de simplificare.
Morfisme de inele
Morfism de inele. Izomorfism. Inele izomorfe.
Corpuri
Noţiunea de corp. Corp comutativ. Exemple de corpuri.
Morfisme de corpuri
Morfism de corpuri, izomorfism de corpuri.
Şiruri de elemente din corpul K
Şir de elemente dintr-un corp. Operaţii cu şiruri de elemente din corpul K. Noţiunea de polinom cu coeficienţi în corpul K.
Forma algebrică a polinoamelor
Forma algebrică a unui monom. Forma algebrică a unui polinom.
Funcţii polinomiale
Funcţie polinomială ataşată unui polinom. Valoarea unui polinom.
Operaţii cu polinoame (1)
Adunarea polinoamelor scrise sub formă algebrică.
Operaţii cu polinoame (2)
Înmulţirea polinoamelor scrise sub formă algebrică.
Operaţii cu polinoame (3)
Împărţirea polinoamelor scrise sub formă algebrică. Teorema împărţirii cu rest.
Împărţirea unui polinom la X-a. Schema lui Horner
Împărţirea unui polinom la X-a. Schema lui Horner.
Divizibilitatea polinoamelor
Divizibilitatea polinoamelor. Proprietăţile relaţiei de divizibilitate. Polinoame asociate în divizibilitate.
Cel mai mare divizor comun şi cel mai mic multiplu comun al polinoamelor
Cel mai mare divizor comun şi cel mai mic multiplu comun al polinoamelor.
Rădăcini ale polinoamelor. Teorema lui Bezout
Rădăcini ale polinoamelor. Teorema lui Bezout. Rădăcini multiple ale unui polinom. Ordin de multiplicitate al rădăcinilor.
Descompunerea polinoamelor în factori ireductibili
Polinoame ireductibilie. Descompunerea polinoamelor în factori ireductibili.
Relaţiile lui Viete
Relaţiile lui Viete pentru polinoame de grad n.
Distanţa între două puncte
Distanţa dintre două puncte în plan când se cunosc coordonatele celor două puncte. Lungimea unui segment. Coordonatele mijlocului unui segment.
Panta unei drepte
Panta unei drepte.
Ecuaţia dreptei determinată de un punct şi o directie dată
Ecuaţia dreptei care trece printr-un punct şi are panta m.
Ecuaţia dreptei determinată de două puncte distincte
Ecuaţia dreptei determinată de două puncte distincte.
Ecuaţia carteziană generală a unei drepte
Ecuaţia carteziană generală a unei drepte.
Condiţii de paralelism a două drepte din plan
Condiţii de paralelism a două drepte din plan.
Distanţa de la un punct la o dreaptă
Formula distanţei de la un punct la o dreaptă.
Aria triunghiului exprimată cu ajutorul coordonatelor vârfurilor sale
Formula ariei triunghiului când se cunosc coordonatele vârfurilor.
Procente
Procente, raport procentual, determinarea procentului dintr-un număr.
Dobânda simplă
Formula de calcul pentru dobănda simplă.
Dobânda compusă
Dobânda compusă. Suma obţinută după o perioadă folosind dobânda compusă.
Taxa pe valoarea adăugată
Taxa pe valoarea adăugată. TVA.
Noţiuni de statistică matematică
Noţiuni de statistică matematică: populaţie statistică, noţiunea de caracteristică a unei populaţii, frecvenţa absolută, frecvenţa relativă, frecvenţa cumulată.
Elemente caracteristice ale unei serii statistice
Interpretarea datelor statistice: media, mediana, modulul, dispersia, abaterea medie pătratică.
Evenimente
Evenimente. Operaţii cu evenimente.
Probabilitatea unui eveniment.
Probabilitatea unui eveniment. Funcţia probabilitate.
Proprietăţi ale probabilităţilor
Operaţii cu probabilităţi. Proprietăţi ale probabilităţilor.
Probabilităţi condiţionate
Probabilităţi condiţionate. Probabilitatea evenimentului A condiţionată de evenimentul B.
Evenimente dependente şi independente
Evenimente dependente şi independente.
Schema lui Poisson
Scheme clasice de probabilitate. Schema lui Poisson (sau schema binomială generalizată).
Schema lui Bernoulli
Scheme clasice de probabilitate. Schema lui Bernoulli (sau schema binomială).
Variabile aleatoare
Variabile aleatoare: tabelul de distribuţie, media, modulul, dispersia şi amplitudinea unei variabile aleatoare.
Limite de șiruri (radicali)
Limite de șiruri, caz de nedeterminare
Limite la infinit ale funcțiilor polinomiale
Limite la infinit ale funcțiilor polinomiale.
Introducere în HTML
HTML este limbajul marcant standard pentru crearea de pagini Web.
HTML reprezintă un început pentru realizarea site-urilor profesionale.
Declarația <! DOCTYPE html> definește acest document ca fiind HTML5.
Elementul <html> este elementul rădăcină al unei pagini HTML.
Elementul <head> conține meta informații despre document.
Elementul <titlu> specifică un titlu pentru document.
Elementul <body> conține conținutul paginii vizibile.
Elementul <h1> definește o rubrică mare.
Elementul <p> definește un alineat.
Editoare HTML
Paginile web pot fi create și modificate folosind editori HTML profesionali.
Elemente de bază HTML
Toate documentele HTML trebuie să înceapă cu o declarație de tip document: <! DOCTYPE html>.
Tag-urile utilizate sunt: <html> și </html>, <body> și </body>, <h1> la <h6>,
<p> și </p>, <a> și </a>, <img>, <ul> și </ul>, <button> și </button>
Elemente HTML
Un element HTML constă, de obicei, dintr-o etichetă de început și o etichetă finală, cu conținutul introdus între ele.
Etichetele folosite sunt: <html> și </html>,<body> și </body> <p> și </p>, <h> și </h>, <br>, <br />.
Atribute HTML
Atributele oferă informații suplimentare despre elementele HTML.
Adresa de legătură este specificată în atributul href.
Numele de fișier al sursei imaginii este specificat în atributul src.
Atributele width și height, care specifică lățimea și înălțimea imaginii.
Atributul alt specifică un text alternativ care trebuie utilizat, dacă nu poate fi afișată o imagine.
Atributul style este utilizat pentru a specifica stilul unui element.
Limbajul este declarat cu atributul lang.
Atributul title este adaugat la elementul <p>.
Titluri HTML
Titlurile (headings) sunt definite cu etichete de la <h1> la <h6>.
Fiecare titlu (heading) HTML are o dimensiune implicită. Cu toate acestea, puteți specifica dimensiunea pentru orice titlu (heading) cu atributul style, folosind proprietatea CSS font-size.
Eticheta <hr> definește o pauză tematică într-o pagină HTML.
Elementul HTML <head> este un container pentru metadate.
Metadatele HTML sunt date despre documentul HTML.
Elementul <head> este plasat între eticheta <html> și eticheta <body>.
Vizualizarea codului sursă HTML se face cu View Page Source.
Inspectarea unui element HTML se face cu Inspect Element.
Paragrafe HTML
Elementul HTML <p> definește un alineat.
Elementul HTML <br> definește o pauză de linie (Line Break).
Folosiți <br> dacă doriți o pauză de linie (o linie nouă) fără a începe un nou paragraf.
Eticheta <br> este o etichetă goală, ceea ce înseamnă că nu are o etichetă finală.
Elementul HTML <pre> definește textul preformatat.
Stiluri HTML
Setarea stilului unui element HTML, se poate face cu atributul style.
Proprietatea CSS background-color definește culoarea de fundal pentru un element
HTML.
Proprietatea CSS color definește culoarea textului pentru un element HTML.
Proprietatea CSS font-family definește fontul care va fi folosit pentru un element HTML.
Proprietatea CSS font-size definește dimensiunea textului pentru un element HTML.
Proprietatea CSS text-align definește alinierea textului orizontal pentru un element HTML.
Formatare text în HTML
Elementele de formatare au fost proiectate pentru a afișa tipuri speciale de text.
<b> definește textul bold, fără nici o importanță suplimentară.
<strong> definește un text intens, cu o importanță „puternică” semantică adăugată.
<i> definește textul italic, fără nicio importanță suplimentară.
<em> definește textul subliniat, cu o importanță semantică adăugată.
<small> definește textul mai mic.
<mark> definește textul marcat / evidențiat.
<del> definește textul șters / eliminat.
<ins> definește textul inserat / adăugat.
<sub> definește textul subscris.
<sup> definește textul suprascriptat.
Elemente de citare și citate în HTML
Elementele de citare folosite în HTML sunt:
<q> definește un citat scurt.
<blockquote> definește o secțiune care este citată dintr-o altă sursă.
<abbr> definește o prescurtare sau un acronim.
<address> definește informațiile de contact (autor / proprietar) ale unui document sau ale unui articol.
<cite> definește titlul unei lucrări.
<bdo> definește înlocuirea bidirecțională.
Comentarii în codul HTML
Etichetele de comentarii sunt utilizate pentru a insera comentarii în codul sursă HTML.
Comentariile nu sunt afișate de browser, dar vă pot ajuta să vă documentați codul sursă HTML.Cu ajutorul comentariilor puteți plasa notificări și memento-uri în HTML.
Comentariile sunt de asemenea foarte bune pentru depanarea HTML, deoarece puteți comenta câteodată liniile de cod HTML pentru a căuta erori:
Culori în HTML
Culorile în codul HTML sunt specificate folosind nume de culori predefinite sau valorile: RGB, HEX, HSL, RGBA, HSLA.
În HTML, o culoare poate fi specificată folosind un nume de culoare.
Puteți seta culoarea de fundal (Background Color) pentru elementele HTML folosind background-color.
Puteți seta culoarea textului folosind color.
Puteți seta culoarea marginilor folosind border.
Saturația poate fi descrisă ca intensitatea unei culori.
Luminozitatea unei culori poate fi descrisă cam cât de multă lumină doriți să dați culorii.
Valorile de culoare RGBA sunt o extensie a valorilor de culoare RGB cu un canal alfa - care specifică opacitatea unei culori.
Valorile de culoare HSLA sunt o extensie a valorilor de culoare HSL cu un canal alfa - care specifică opacitatea unei culori.
Stiluri CSS în HTML
Modelarea HTML cu CSS.
CSS descrie modul în care elementele HTML trebuie să fie afișate pe ecran, pe hârtie sau în alte suporturi. Poate controla aspectul mai multor pagini web simultan.
Utilizați atributul HTML style pentru stilul CSS în linie (inline).
Utilizați elementul HTML <style> pentru a defini stilul CSS intern.
Utilizați elementul HTML <link> pentru a vă referi la un fișier CSS extern.
Utilizați elementul HTML <head> pentru a stoca elementele <style> și <link>.
Utilizați proprietatea CSS color pentru culorile de text.
Utilizați proprietatea CSS font-family pentru fonturile text.
Utilizați proprietatea CSS font-size pentru dimensiunile textului.
Utilizați proprietatea CSS border pentru margini.
Utilizați proprietatea CSS padding pentru spațiu în interiorul border.
Utilizați proprietatea CSS margin pentru spațiu în afara border.
Pentru a defini un stil specific pentru un element special, adăugați un atribut id elementului:
Pentru a defini un stil pentru tipuri speciale de elemente, adăugați un atribut de clasă elementului:
Foile de stil externe (external style sheets ) pot fi trimise cu o adresă URL completă sau cu o cale relativă la pagina web curentă.
Linkuri HTML
Linkurile se găsesc în aproape toate paginile web. Link-urile permit utilizatorilor să facă click pe drumul lor de la pagină la pagină.
Link-urile HTML sunt hyperlink-uri.
Utilizați elementul <a> pentru a defini un link.
Utilizați atributul href pentru a defini adresa link-ului.
Utilizați atributul țintă (target) pentru a defini unde să deschideți documentul legat.
Utilizați elementul <img> (în interiorul <a>) pentru a utiliza o imagine ca link.
Utilizați atributul id (id = "valoare") pentru a defini marcajele (bookmarks) dintr-o pagină
Atributul title specifică informații suplimentare despre un element.
Utilizați atributul href (href = "# valoare") pentru a face legătura cu marcajul (bookmark).
Marcajele HTML (bookmarks) sunt utilizate pentru a permite cititorilor să sară la anumite părți ale unei pagini Web.
Paginile externe pot fi referite cu o adresă URL completă sau cu o cale relativă la pagina web curentă.
Imagini în HTML
Imaginile pot îmbunătăți designul și aspectul unei pagini web.
Utilizați elementul HTML <img> pentru a defini o imagine.
Utilizați atributul HTML src pentru a defini adresa URL a imaginii.
Utilizați atributul HTML alt pentru a defini un text alternativ pentru o imagine, dacă nu poate fi afișat.
Utilizați atributele HTML lățime și înălțime (width and height) pentru a defini dimensiunea imaginii.
Utilizați proprietățile CSS pentru lățime și înălțime (width and height) pentru a defini dimensiunea imaginii (alternativ).
Utilizați proprietatea CSS float pentru a lăsa imaginea să plutească.
Utilizați elementul HTML <map> pentru a defini o imagine-hartă (image-map).
Utilizați elementul HTML <area> pentru a defini zonele în care se poate face click pe imaginea hartă (image-map).
Utilizați atributul usemap al elementului HTML <img> pentru a indica o hartă-imagine(image-map).
Utilizați elementul HTML <picture> pentru a afișa imagini diferite pentru diferite dispozitive.
Imagini hărți în HTML
Cu hărți de imagine (Image Maps), puteți adăuga zone pe care se poate face click pe o imagine.
Eticheta <map> definește o imagine-hartă
Imaginea este introdusă folosind eticheta <img>.Singura diferență față de alte imagini este că trebuie să adăugați un atribut usemap.
Elementul <map> este utilizat pentru a crea o hartă a imaginii și este legat de imagine prin utilizarea atributului nume.
O zonă pe care se poate face click este definită folosind un element <area>.
Imagini de fundal în HTML
O imagine de fundal poate fi specificată pe aproape orice element HTML.
Pentru a adăuga o imagine de fundal în HTML, folosiți imaginea de fundal (background-image) a proprietății CSS.
Pentru a adăuga o imagine de fundal (background-image) la un element HTML, puteți utiliza atributul style.
Dacă doriți ca întreaga pagină să aibă o imagine de fundal (background-image), atunci trebuie să specificați imaginea de fundal (background-image) în elementul <body>.
Dacă imaginea de fundal este mai mică decât elementul, imaginea se va repeta, orizontal și vertical, până când va ajunge la sfârșitul elementului.
Pentru a evita ca imaginea de fundal (background-image)să se repete, utilizați proprietatea background-repeat.
Dacă doriți ca imaginea de fundal să acopere întregul element, puteți seta proprietatea de fundal (background-size) pe care să o acopere.
De asemenea, pentru a vă asigura că întregul element este întotdeauna acoperit, setați proprietatea de atașare în fundal la fix (background-attachment).
Dacă doriți ca întinderea imaginii de fundal să se potrivească întregii imagini din element, puteți seta proprietatea de fundal (background-size) la 100% 100%:
Element de imagine în HTML
Elementul de imagine ne permite să afișăm imagini diferite pentru diferite dispozitive sau dimensiuni de ecran.
Elementul HTML <picture>.
Elementul <picture> conține o serie de elemente <source>.
Elementul <img> este folosit de browserele care nu acceptă elementul <picture> sau dacă niciuna dintre etichetele <source> nu se potrivește.
Există două scopuri principale pentru elementul <picture>: Lățime de bandă (Bandwidth), Formatați suportul (Format Support).
Tabele HTML
Utilizați elementul HTML <table> pentru a defini un tabel.
Utilizați elementul HTML <tr> pentru a defini un rând de tabel.
Utilizați elementul HTML <td> pentru a defini datele unui tabel.
Utilizați elementul HTML <th> pentru a defini un titlu de tabel.
Utilizați elementul HTML <caption> pentru a defini o legendă de tabel.
Utilizați proprietatea CSS border pentru a defini o bordură.
Utilizați proprietatea CSS border-collapse pentru a restrânge marginile celulelor.
Utilizați proprietatea CSS padding pentru a adăuga umplutură la celule.
Utilizați proprietatea CSS text-align pentru a alinia textul celulelor.
Utilizați proprietatea CSS border-spacing pentru a seta distanța dintre celule.
Utilizați atributul colspan pentru a crea o celulă cu mai multe coloane.
Utilizați atributul linespan pentru a face ca o celulă să aibă mai multe rânduri.
Utilizați atributul id pentru a defini în mod unic o tabelă.
<colgroup> Specifică un grup de una sau mai multe coloane dintr-un tabel pentru formatare.
<col> Specifică proprietățile coloanei pentru fiecare coloană dintr-un element <colgroup>.
<thead> Grupează conținutul antetului într-un tabel.
<tbody> Grupează conținutul corpului într-un tabel.
<tfoot> Grupează conținutul subsolului într-un tabel.
Liste HTML
Elementele din listă pot conține alte elemente HTML
Utilizați elementul HTML <ul> pentru a defini o listă neordonată.
Utilizați proprietatea CSS list-style-type pentru a defini marcajul elementelor de listă.
Utilizați elementul HTML <ol> pentru a defini o listă ordonată.
Utilizați atributul HTML type pentru a defini tipul de numerotare.
Utilizați elementul HTML <li> pentru a defini un element de listă.
Utilizați elementul HTML <dl> pentru a defini o listă de descrieri.
Utilizați elementul HTML <dt> pentru a defini termenul de descriere.
Utilizați elementul HTML <dd> pentru a descrie termenul dintr-o listă de descrieri.
Listele pot fi amplasate în liste.
Elementele din listă pot conține alte elemente HTML.
Utilizați proprietatea CSS float: left sau display:inline pentru a afișa o listă pe orizontală.
Proprietatea CSS list-style-type este utilizată pentru a defini stilul marcajului articolului de listă:
disc - Setează marcajul elementului listei la un buletin (implicit).
circle - Setează marcajul elementului de listă într-un cerc.
square - Setează marcajul elementului de listă într-un pătrat.
none - Elementele din listă nu vor fi marcate.
Elementele HTML Block și Inline
Fiecare element HTML are o valoare de afișare implicită în funcție de tipul de element.Cele două valori afișate sunt: block și inlinie.
Un element la nivel de block (block-level element) pornește întotdeauna pe o linie nouă și ocupă toată lățimea disponibilă (se întinde spre stânga și spre dreapta, cât poate).
Elementul <div> este un element la nivel de block.
Un element inline nu pornește de pe o linie nouă ci ocupă doar lățimea necesară.
Acesta este un element inline <span> din interiorul unui paragraf.
Elementul <div> este adesea folosit ca și container pentru alte elemente HTML.
Elementul <div> nu are atribute necesare, dar stilul (style), clasa (class) și id-ul (id) sunt comune.
Când este utilizat împreună cu CSS, elementul <div> poate fi utilizat pentru a aplica stiluri blocurilor de conținut.
Elementul <span> este adesea folosit ca un container pentru un text.
Elementul <span> nu are atribute necesare, stilul (style), clasa (class) și id-ul (id) sunt comune.
Când este utilizat împreună cu CSS, elementul <span> poate fi utilizat pentru a aplica stiluri blocurilor de conținut.
Atributul HTML class
Atributul HTML class este folosit pentru a defini stiluri egale pentru elemente cu același nume de clasă.
Atributul HTML class poate fi folosit și pe elementele inline.
În CSS, pentru a selecta elemente cu o anumită clasă, scrieți un caracter (.), urmat de numele clasei.
Atributul class poate fi folosit pe orice element HTML.
Numele clasei este sensibil la litere mari și mici!
Elementele HTML pot avea mai mult de un nume de clasă, fiecare nume de clasă trebuie separat printr-un spațiu.
Etichetele diferite pot împărtăși aceeași clasă.
Etichetele diferite, cum ar fi <h2> și <p>, pot avea același nume de clasă și, prin urmare, au același stil.
Utilizarea atributului class în JavaScript.
JavaScript poate accesa elemente cu un nume de clasă specificat folosind metoda getElementsByClassName ().
Atributul HTML id
Atributul id specifică un id unic pentru un element HTML (valoarea trebuie să fie unică în documentul HTML).
Valoarea id poate fi folosită de CSS și JavaScript pentru a efectua anumite sarcini pentru elementul cu valoarea specifică de id.
În CSS, pentru a selecta un element cu un id specific, scrieți un caracter hash (#), urmat de id-ul elementului.
Valoarea id este sensibilă la litere mari și mici.
Atributul id poate fi utilizat pe orice element HTML.
Un element HTML poate avea un singur id unic care aparține acelui element singular, în timp ce un nume de clasă poate fi utilizat de mai multe elemente.
Marcajele (bookmarks) HTML sunt utilizate pentru a permite cititorilor să sară la anumite părți ale unei pagini Web.
Marcajele (bookmarks) pot fi utile dacă pagina dvs. web este foarte lungă.
Utilizarea atributului id în JavaScript.
JavaScript poate accesa un element cu un id specificat folosind metoda getElementById ().
HTML Iframes
Un iframe este utilizat pentru a afișa o pagină web în cadrul unei pagini web.
Un iframe HTML este definit cu eticheta <iframe>.
Atributul src specifică adresa URL (adresa web) a paginii inline frame.
Utilizați atributele height și width (înălțime și lățime) pentru a specifica dimensiunea iframei.
Sau puteți utiliza CSS pentru a seta height și width (înălțimea și lățimea) iframe-ului.
În mod implicit, un iframe are un chenar (border) în jurul său.
Pentru a elimina chenarul (border), adăugați atributul style și utilizați proprietatea CSS border.
Cu CSS, puteți modifica, de asemenea, dimensiunea, stilul și culoarea marginii iframe.
Un iframe poate fi folosit ca target frame pentru o legătură.
Atributul target al linkului trebuie să se refere la atributul name al iframe:
<iframe> Definește un cadru inline.
HTML JavaScript
JavaScript face ca paginile HTML să fie mai dinamice și mai interactive.
Eticheta <script> este utilizată pentru a defini un script din partea clientului (client-side script) (JavaScript).
Elementul <script> fie conține instrucțiuni script, fie indică prin atributul src un fișier script extern.
Pentru a selecta un element HTML, JavaScript utilizează cel mai adesea metoda document.getElementById ().
JavaScript poate schimba conținutul HTML.
JavaScript poate schimba stilurile HTML.
JavaScript poate schimba atributele HTML.
Eticheta <noscript> este utilizată pentru a furniza un conținut alternativ pentru utilizatorii care au scripturi dezactivate în browserul lor sau au un browser care nu acceptă scripturile din partea clientului.
Căi de fișiere în HTML
O cale de fișier descrie locația unui fișier în structura folderului unui site web.
Căile de fișiere sunt utilizate la conectarea la fișiere externe, cum ar fi: Pagini web, Imagini, Foi de stil, JavaScripts.
O cale absolută a fișierului este adresa URL completă a unui fișier internet.
O cale de fișier relativă indică un fișier relativ la pagina curentă.
Elementul HTML head
Elementul <head> este un container pentru metadate (date despre date) și este plasat între eticheta <html> și eticheta <body>.
<head> Definește informații despre document.
<titlu> Defineste titlul unui document.
<base> Definește o adresă implicită sau o țintă implicită pentru toate linkurile dintr-o pagină.
<link> Definește relația dintre un document și o resursă externă.
<meta> Definește metadatele despre un document HTML.
<script> Definește un script din partea clientului.
<style> Definește informațiile despre stil pentru un document.
HTML5 a introdus o metodă pentru a permite proiectanților web să preia controlul asupra viewport-ului, prin eticheta <meta>.
Viewport este zona vizibilă a utilizatorului unei pagini web. Aceasta variază în funcție de dispozitiv și va fi mai mică pe un telefon mobil decât pe ecranul computerului.
Ar trebui să includeți următorul element viewport <meta> în toate paginile web.
Partea width=device-width stabilește lățimea paginii pentru a urma lățimea ecranului dispozitivului (care va varia în funcție de dispozitiv).
Partea initial-scale=1.0 setează nivelul inițial de zoom când prima pagină este încărcată de browser.
Elemente HTML Layout
Site-urile web deseori afișează conținut în mai multe coloane (cum ar fi o revistă sau un ziar).
<header> - definește un antet pentru un document sau o secțiune
<nav> - definește un container pentru link-uri de navigație
<section> - definește o secțiune dintr-un document
<article> - definește un articol independent de sine stătător
<aside> - definește conținutul în afară de conținut (precum o bară laterală)
<footer> - definește un subsol pentru un document sau o secțiune
<detalii> - definește detalii suplimentare
<summary> - definește un titlu pentru elementul <details>
Tehnici Layout HTML. Există cinci moduri diferite de a crea multicolumn layouts: HTML tables (not recommended), CSS float property, CSS flexbox, CSS framework, CSS grid.
Elementul <table> nu a fost proiectat pentru a fi un instrument de aspect! Scopul elementului <tabel> este afișarea datelor tabulare.
Dacă doriți să vă creați rapid un layout, puteți utiliza un framework cum ar fi Bootstrap.
Este ceva comun să faceți machete web (web layouts) întregi folosind proprietatea CSS float.
Flexbox reprezintă un nou mod de dispunere în CSS3.
Modulul CSS Grid Layout oferă un sistem de dispunere bazat pe grilă, cu rânduri și coloane, ceea ce facilitează proiectarea paginilor web fără a fi nevoie să folosiți floats și poziționare.
HTML Responsive Web Design
Responsive Web Design vizează utilizarea HTML-ului și CSS-ului pentru redimensionarea, ascunderea, micșorarea sau mărirea unui site web automat, pentru a-l arăta bine pe toate dispozitivele (desktop-uri, tablete și telefoane).
Setarea Viewport. Când creați pagini web responsive, adăugați următorul element <meta> în toate paginile dvs. web.
Imaginile responsive sunt imagini care se dimensionează frumos pentru a se potrivi cu orice dimensiune a browserului.
Utilizarea proprietății lățime (width).
Utilizarea proprietății cu lățimea maximă (max-width).
Elementul HTML <picture> vă permite să definiți imagini diferite pentru dimensiuni diferite ale ferestrei browserului.
Responsive Text Size. Mărimea textului poate fi setată cu o unitate „vw”, ceea ce înseamnă „lățimea vizualizării” (viewport width).
Pe lângă redimensionarea textului și a imaginilor, este de asemenea obișnuit să folosești interogări media în paginile responsive web.
Cu interogări media, puteți defini stiluri complet diferite pentru diferite dimensiuni de browser.
O pagină Responsive Web ar trebui să arate bine pe ecrane desktop mari și pe telefoane mobile mici.
Există multe CSS Frameworks care oferă un Responsive Design.
O modalitate excelentă de a crea un Responsive Design este de a utiliza o responsive style sheet.
Un alt framework popular este Bootstrap, folosește HTML, CSS și jQuery pentru a face pagini web responsive.
Elemente de cod HTML pentru computer
Elementele de cod HTML pentru computer sunt:
<code> Defineste codul de programare.
<kbd> Definește introducerea tastaturii.
<samp> Definește ieșirea computerului.
<var> Definește o variabilă.
<pre>Definește un text preformatat.
Entități HTML
Caracterele rezervate în HTML trebuie înlocuite cu entități de caractere.
Caracterele care nu sunt prezente pe tastatură pot fi, de asemenea, înlocuite de entități.
Simboluri HTML
Multe simboluri matematice, tehnice și simboluri valutare nu sunt prezente pe o tastatură normală.
Pentru a adăuga astfel de simboluri la o pagină HTML, puteți utiliza un nume de entitate HTML.
Simboluri matematice acceptate de HTML: forall, part, exist, empty, nabla, isin, notin, ni, prod, sum.
Câteva litere grecești acceptate de HTML:Alpha, Beta, Gamma, Delta, Epsilon, Zeta.
Câteva entități acceptate de HTML:copy, euro, trade, larr, uarr, rarr, darr, clubs, diams.
Codare HTML (seturi de caractere)
Pentru a afișa corect o pagină HTML, un browser web trebuie să știe ce set de caractere să folosească.
ASCII a fost primul standard de codare a caracterelor (numit și set de caractere).
ISO-8859-1 a fost setul de caractere implicit pentru HTML 4
ANSI (Windows-1252) a fost setul de caractere Windows original.
UTF-8 (Unicode) acoperă aproape toate caracterele și simbolurile din lume.
Setul de caractere implicit pentru HTML5 este UTF-8.
Atributul HTML charset.
Pentru a afișa corect o pagină HTML, un browser web trebuie să cunoască setul de caractere utilizat în pagină.
Acest lucru este specificat în eticheta <meta>.
HTML Uniform Resource Locators (URL)
Un URL este un alt cuvânt pentru o adresă web.
O adresă URL poate fi compusă din cuvinte (lectii-virtuale.ro) sau o adresă IP (Internet Protocol) (192.68.21.51).
Majoritatea oamenilor introduc numele când navighează, deoarece numele sunt mai ușor de reținut decât numerele.
scheme - definește tipul serviciului de internet (cel mai frecvent este http sau https)
prefix - definește un prefix de domeniu (implicit pentru http este www)
domain - definește numele domeniului Internet (cum ar fi lectii-virtuale.ro)
port - definește numărul de port la gazdă (implicit pentru http este 80)
path - definește o cale pe server (Dacă este omis: directorul rădăcină al site-ului)
filename - definește numele unui document sau resursă
Scheme URL comune: HyperText Transfer Protocol (http), Secure HyperText Transfer Protocol (https), File Transfer Protocol (ftp).
Codificare URL.
Adresele URL pot fi trimise doar pe Internet folosind setul de caractere ASCII. Dacă o adresă URL conține caractere în afara setului ASCII, adresa URL trebuie convertită.
Codarea URL transformă caracterele care nu sunt ASCII într-un format care poate fi transmis pe internet.
Codarea URL înlocuiește caracterele care nu sunt ASCII cu un „%” urmat de cifre hexadecimale.
Adresele URL nu pot conține spații. Codarea URL înlocuiește în mod normal un spațiu cu un semn plus (+) sau% 20.
Setul de caractere implicit în HTML5 este UTF-8.
HTML și XHTML
XHTML este HTML scris ca XML.
XHTML înseamnă limbaj de extindere HyperText Markup Language
XHTML este aproape identic cu HTML
XHTML este mai strict decât HTML
XHTML este HTML definit ca o aplicație XML
XHTML este acceptat de toate browserele principale
Formulare HTML
Elementul HTML <form> definește un formular care este utilizat pentru a colecta intrarea utilizatorului.
Elementele de formular sunt diferite tipuri de elemente de intrare, cum ar fi câmpurile de text, casetele de selectare, butoanele radio, butoanele de trimitere și multe altele.
Elementul <input> este cel mai important form element.
Elementul <input> poate fi afișat în mai multe moduri, în funcție de atributul type.
<input type = "text"> Definește un câmp de introducere text dintr-o linie.
<input type = "radio"> Definește un buton radio (pentru selectarea uneia dintre mai multe opțiuni).
<input type = "submit"> Definește un buton de trimitere (pentru trimiterea formularului).
Form-handler este de obicei o pagină de server cu un script pentru procesarea datelor de intrare.
Form-handler este specificat în atributul de acțiune al formularului.
Atributul action definește acțiunea care trebuie executată la trimiterea formularului.
Atributul target specifică dacă rezultatul trimis se va deschide într-o nouă pagină a browser-ului, într-un cadru sau în fereastra curentă.
Valoarea implicită este „_self”, ceea ce înseamnă că formularul va fi transmis în fereastra curentă.
Pentru a face ca rezultatul formularului să fie deschis într-o nouă pagină a browser-ului, folosiți valoarea „_blank”.
Atributul method specifică metoda HTTP (GET sau POST) care trebuie utilizată la trimiterea datelor formularului.
Trimiterea datelor formularului se face cu metoda implicită GET.
Utilizați întotdeauna POST dacă datele din formular conțin informații personale sau sensibile. Metoda POST nu afișează datele formularului trimis în câmpul adresei paginii.
Elementul <fieldset> este utilizat pentru a grupa datele înrudite într-un formular.
Elementul <legend> definește o legendă pentru elementul <fieldset>.
Elemente de formulare HTML
<form> Definește un formular HTML pentru introducerea utilizatorului.
Cel mai important element de formă este elementul <input>.
Elementul <input> poate fi afișat în mai multe moduri, în funcție de atributul type.
Dacă atributul type este omis, câmpul de intrare primește tipul implicit: "text".
Elementul <select> definește o listă derulantă (drop-down list).
Elementul <option> definește o opțiune care poate fi selectată.
Utilizați atributul size pentru a specifica numărul de valori vizibile.
Utilizați atributul multiple pentru a permite utilizatorului să selecteze mai multe valori.
Elementul <textarea> definește un câmp de introducere pe mai multe linii (o zonă de text).
Atributul rows specifică numărul vizibil de linii dintr-o zonă de text.
Atributul cols specifică lățimea vizibilă a unei zone de text.
Elementul <button> definește un buton pe care se poate face click.
Elementul <datalist> specifică o listă de opțiuni predefinite pentru un element <input>.
Utilizatorii vor vedea o listă derulantă (drop-down list) a opțiunilor predefinite pe măsură ce introduc date.
Atributul listei elementului <input>, trebuie să se refere la atributul id al elementului <datalist>.
Elementul <output> reprezintă rezultatul unui calcul (ca unul realizat de un script).
<form> Definește un formular HTML pentru introducerea utilizatorului
<input> Definește un control de intrare
<textarea> Definește un control de intrare multilin (zona text)
<label> Definește o etichetă pentru un element <input>
<fieldset> Grupează elemente conexe într-o formă
<legend> Definește o legendă pentru un element <fieldset>
<select> Definește o listă derulantă
<optgroup> Definește un grup de opțiuni conexe dintr-o listă derulantă
<option> Definește o opțiune dintr-o listă derulantă
<button> Definește un buton pe care se poate face clic
<datalist> Specifică o listă de opțiuni predefinite pentru controale de intrare
<output> Definește rezultatul unui calcul
HTML Tipuri Input
Acest capitol descrie diferitele tipuri de intrare pentru elementul <input>.
Diferite tipuri de intrare pe care le puteți utiliza în HTML:<input type="button">, <input type="checkbox">, <input type="color">,
<input type="date">, <input type="datetime-local">, <input type="email">, <input type="file">, <input type="hidden">
<input type="image">, <input type="month">, <input type="number">, <input type="password">, <input type="radio">
<input type="range">, <input type="reset">, <input type="search">, <input type="submit">, <input type="tel">
<input type="text">, <input type="time">, <input type="url">, <input type="week">.
HTML5 a adăugat mai multe tipuri noi de intrare: color, date, datetime-local, email, month, number, range, search, tel, time, url, week.
Restricții de intrare: checked, disabled, max, maxlength, min, pattern, readonly, required, size, step, value.
<input type = ""> Specifică tipul de intrare de afișat.
HTML Atribute Input
Atributul value specifică valoarea inițială pentru un câmp de intrare.
Atributul readonly specifică faptul că un câmp de intrare este doar citit (nu poate fi modificat).
Atributul disabled specifică faptul că un câmp de intrare este dezactivat.
Atributul size specifică dimensiunea (în caractere) pentru câmpul de intrare.
Atributul maxlength specifică lungimea maximă permisă pentru câmpul de intrare.
Restricțiile de intrare nu sunt ignorate, iar JavaScript oferă multe modalități de a adăuga input-uri ilegale.
HTML5 a adăugat următoarele atribute pentru <input>: autocomplete, autofocus, form, formaction, formenctype, formmethod,
formnovalidate, formtarget, height and width, list, min and max, multiple, pattern (regexp), placeholder, required, step
și următoarele atribute pentru <form>: autocomplete, novalidate.
Atributul formaction este utilizat cu type="submit" și type="image".
Atributul formenctype este utilizat cu type = "submit" și type = "image".
Atributul formmethod poate fi utilizat cu type = "submit" și type = "image".
Atributul step funcționează cu următoarele tipuri de intrare (input types): number, range, date, datetime-local, month, time și week.
Atributul pattern funcționează cu următoarele tipuri de intrare (input types): text, search, url, tel, email, și password.
Utilizați atributul global title pentru a descrie pattern-ul care să ajute utilizatorul.
Atributul placeholder funcționează cu următoarele tipuri de intrare (input types): text, search, url, tel, email, și password.
Atributul required funcționează cu următoarele tipuri de intrare (input types): text, search, url, tel, email, password, date pickers, number, checkbox, radio, și file.
Atributul multiple funcționează cu următoarele tipuri de intrare (input types): e-mail și file.
Atributele min și max funcționează cu următoarele tipuri de intrare (input types): number, range, date, datetime-local, month, time și week.
Atributul list se referă la un element <datalist> care conține opțiuni predefinite pentru un element <input>.
Atributele înălțime și lățime (height și width) specifică înălțimea și lățimea unui element <input type = "image">.
Atributul formnovalidate poate fi utilizat cu type="submit".
Atributul formtarget înlocuiește atributul țintă (target) al elementului <form>.
Atributul formtarget poate fi utilizat cu type = "submit" și type = "image".
Atributul novalidate este un atribut <form>.
Atributul autocomplete funcționează cu <form> și următoarele tipuri <input>:text, search, url, tel, email, password, datepickers, range, și color.
Introducere în HTML5
WHATWG a dorit să dezvolte HTML ca un „standard de viață”. Un nivel de viață este mereu actualizat și îmbunătățit. Se pot adăuga noi funcții, dar funcționalitățile vechi nu pot fi eliminate.
Declarația DOCTYPE pentru HTML5.
Declarația de codare a caracterelor (charset).
Codificarea implicită a caracterelor în HTML5 este UTF-8.
Elementesemantice noi precum: <header>, <footer>, <article> și <section>.
Atribute ale elementelor de formular noi, cum ar fi: number, date, time, calendar, și range.
Elemente grafice noi: <svg> și <canvas>.
Elemente multimedia noi: <audio> și <video>.
Cele mai interesante API-uri noi în HTML5 sunt: HTML Geolocation, HTML Drag and Drop, HTML Local Storage, HTML Application Cache, HTML Web Workers, HTML SSE.
Următoarele elemente HTML4 au fost eliminate în HTML5: <acronym>, <applet>, <basefont>, <big>, <center>, <dir>, <font>, <frame>, <frameset>,
<noframes>, <strike>, <tt>.
Folosiți în schimb: <abbr>, <object>, CSS, <ul>, <s>, <del>.
Suport HTML5
HTML5 este acceptat în toate browserele moderne.
În plus, toate browserele, vechi și noi, gestionează automat elemente nerecunoscute ca elemente inline.
Din această cauză, puteți „învăța” browserele mai vechi să gestioneze elemente HTML „necunoscute”.
Puteți învăța browserele mai vechi să gestioneze corect HTML5.
HTML5 definește opt noi elemente semantice. Toate acestea sunt elemente la nivel de bloc (block-level elements).
Pentru a asigura un comportament corect în browserele mai vechi, puteți seta proprietatea de afișare CSS (CSS display property) pentru aceste elemente HTML pentru a le bloca.
Puteți adăuga, de asemenea, unei pagini HTML, elemente noi folosind un truc de browser.
Declarația JavaScript document.createElement ("myHero") este necesară pentru a crea un element nou în IE 9 și în versiunile anterioare.
Veți avea nevoie de HTML5Shiv pentru a oferi compatibilitate pentru browsere IE mai vechi decât IE 9.
HTML5Shiv este plasat în eticheta <head>.
HTML5Shiv este un fișier javascript la care se face referire într-o etichetă <script>.
Ar trebui să utilizați HTML5Shiv când utilizați noile elemente HTML5 precum: <article>, <section>, <aside>, <nav>, <footer>.
Elemente noi în HTML5
HTML5 oferă elemente noi pentru o structură mai bună a documentelor:
<article> - Definește un articol dintr-un document
<aside> - Definește conținutul în afară de conținutul paginii
<bdi> - Izolează o parte a textului care ar putea fi formatată într-o direcție diferită de celălalt text din afara acestuia
<detalii> - Definește detalii suplimentare pe care utilizatorul le poate vizualiza sau ascunde
<dialog> - Definește o casetă de dialog sau o fereastră
<figcaption> - Definește o legendă pentru un element <figure>
<figure> - Definește conținut autonom
<footer> - Definește un subsol pentru un document sau secțiune
<header> - Definește un antet pentru un document sau secțiune
<principal> - Definește conținutul principal al unui document
<mark> - Definește text marcat / evidențiat
<meter> - Definește o masurare scalara intr-un interval cunoscut (un ecartament)
<nav> - Definește legăturile de navigare
<progress> - Reprezintă progresul unei sarcini
<rp> - Definește ce trebuie afișat în browserele care nu acceptă adnotările ruby
<rt> - Definește o explicație / pronunție a caracterelor (pentru tipografia din Asia de Est)
<ruby> - Definește o adnotare rubin (pentru tipografia din Asia de Est)
<section> - Definește o secțiune dintr-un document
<summary> - Definește un titlu vizibil pentru un element <details>
<time> - Definește o data / ora
<wbr> - Definește o posibila pauza de linie
Elemente noi de formular (New Form Elements):
<datalist> - Specifică o listă de opțiuni predefinite pentru controale de intrare
<output> - Definește rezultatul unui calcul
Tipuri noi de intrare (New Input Types): color,date,datetime,datetime,local,email,month,number,range,search,tel,time,url,week,autocomplete,autofocus,form,formaction,formenctype,formmethod,formnovalidate,formtarget,height and width,list,min and max,multiple,pattern (regexp),placeholder,required,step.
Grafică HTML5:
<canvas> Desenați grafică din mers, prin scripturi (de obicei JavaScript)
<svg> Desenați grafică vectorială scalabilă
Elemente media noi:
<audio> - Definește conținutul sunetului
<embed> - Definește un container pentru o aplicație externă (non-HTML)
<source> - Definește mai multe resurse media pentru elemente media (<video> și <audio>)
<track> - Definește piesele text pentru elementele media (<video> și <audio>)
<video> - Defineste video sau film
Elemente semantice în HTML5
Semantica se referă la studiul sensurilor cuvintelor și frazelor dintr-o limbă.
Elemente semantice = elemente cu semnificație:
<article>, <aside>, <details>, <figcaption>, <figure>, <footer>, <header>, <main>, <mark>, <nav>, <section>, <summary>, <time>.
Exemple de elemente non-semantice: <div> și <span> - Nu spune nimic despre conținutul său.
Exemple de elemente semantice: <form>, <tabel> și <article> - definește clar conținutul său.
<article> Definește un articol
<aside> Definește conținutul în afară de conținutul paginii
<detalii> Definește detalii suplimentare pe care utilizatorul le poate vizualiza sau ascunde
<figcaption> Definește o legendă pentru un element <figure>
<figure> Specifică conținut independent, cum ar fi ilustrații, diagrame, fotografii, listări de coduri etc.
<footer> Definește un subsol pentru un document sau secțiune
<header> Specifică un antet pentru un document sau secțiune
<main> Specifică conținutul principal al unui document
<mark> Definește text marcat / evidențiat
<nav> Definește legăturile de navigare
<section> Definește o secțiune dintr-un document
<summary> Definește un titlu vizibil pentru un element <details>
<time> Definește o data / ora
Migrare în HTML5
Acest capitol se referă în întregime la modul de migrare de la HTML4 la HTML5.
Acest capitol arată cum se poate converti o pagină HTML4 într-o pagină HTML5, fără a distruge nimic din conținutul sau structura originală.
Migrarea de la HTML4 la HTML5:
<div id="header"> - <header>
<div id="menu"> - <nav>
<div id="content"> - <section>
<div class="article"> - <article>
<div id="footer"> - <footer>
Modificați doctype la doctype HTML5.
Modificați informațiile de codificare la codarea HTML5.
Adăugați HTML5Shiv.
Schimbare la elemente semantice HTML5.
CSS-ul existent conține ID-uri și clase pentru stilizarea elementelor.
Înlocuiți cu stiluri CSS egale pentru elemente semantice HTML5.
Schimbați elementele în elemente semantice HTML5.
Există o diferență confuză (lipsa) în standardul HTML5, între <article> <section> și <div>.
În standardul HTML5, elementul <secțiune> este definit ca un bloc de elemente conexe.
Elementul <article> este definit ca un bloc complet, de sine stătător, al elementelor conexe.
Elementul <div> este definit ca un bloc de elemente pentru copii.
<article> în <article>.
<div> în <article>.
<div> în <section> în <article>.
Ghid de stil în HTML5
O utilizare constantă a stilului face mai ușor pentru alții să înțeleagă HTML-ul.
În viitor, programe precum cititorii XML ar putea dori să citească HTML-ul.
Utilizarea unei sintaxe bine formate - „aproape de XHTML” poate fi inteligentă.
Vă recomandăm să folosiți numele elementelor scrise cu litere mici, deoarece:
În HTML5, nu trebuie să închideți toate elementele (de exemplu elementul <p>).
Vă recomandăm să închideți toate elementele HTML.
Închideți elementele HTML goale
În HTML5, este opțional să închideți elementele goale.
HTML5 permite amestecarea literelor mari și a literelor mici în nume de atribute.
Vă recomandăm să folosiți nume de atribute scrise culitere mici.
HTML5 permite ca valorile atributelor să fie scrise fără ghilimele.
Vă recomandăm să puneți între ghilimele valorile atributului.
Adăugați întotdeauna atributul alt la imagini. Acest atribut este important atunci când imaginea din anumite motive nu poate fi afișată. De asemenea, definiți întotdeauna lățimea și înălțimea (width și height) imaginii. Reduce pâlpâirea, deoarece browserul poate rezerva spațiu pentru imagine înainte de încărcare.
HTML5 permite spații în jurul semnelor egale. Dar fără spațiu este mai ușor de citit și grupează entitățile mai bine împreună.
Când utilizați un editor HTML, este incomod să derulați la dreapta și la stânga pentru a citi codul HTML.
Încercați să evitați liniile de cod mai lungi de 80 de caractere.
Nu adăugați linii necompletate fără un motiv.
Pentru lizibilitate, adăugați linii goale pentru a separa blocuri de coduri mari sau logice.
Pentru lizibilitate, adăugați două spații de indentare. Nu folosiți tasta tab.
Nu folosiți linii necompletate și indentate. Nu este necesar să indentizați fiecare elemen
În HTML5, eticheta <html> și eticheta <body> pot fi omise.
Nu vă recomandăm să omiteți etichetele <html> și <body>.
Elementul <html> este rădăcina documentului. Este locul recomandat pentru specificarea limbii paginii.
Omiterea <html> sau <body> poate bloca software-ul DOM și XML.
Omiterea <body> poate produce erori în browserele mai vechi (IE9).
În HTML5, eticheta <head> poate fi omisă.
În mod implicit, browserele vor adăuga toate elementele înainte de <body> la un element implicit <head>.
Puteți reduce complexitatea HTML prin omiterea etichetei <head>
Elementul <title> este necesar în HTML5. Faceți titlul cât mai semnificativ posibil
HTML5 a introdus o metodă pentru a permite proiectanților web să preia controlul asupra viewport-ului, prin eticheta <meta>.
Viewport este zona vizibilă a utilizatorului unei pagini web. Acesta variază în funcție de dispozitiv și va fi mai mic pe un telefon mobil decât pe ecranul computerului.
Lățimea (width) = partea lățimii dispozitivului (width=device-width part) - stabilește lățimea paginii pentru a urma lățimea ecranului dispozitivului (screen-width) (care va varia în funcție de dispozitiv).
Partea inițială = 1,0 setează nivelul de zoom inițial atunci când pagina este încărcată prima dată de browser
Comentariile scurte trebuie scrise pe o singură linie
Comentariile lungi sunt mai ușor de observat dacă sunt indentate în două spații.
Utilizați sintaxa simplă pentru a face legătura cu foile de stil (atributul tip nu este necesar)
Regulile scurte pot fi comprimate
Regulile lungi trebuie scrise pe mai multe rânduri
Puneți suportul de deschidere (opening bracket) pe aceeași linie cu selectorul.
Utilizați un spațiu înainte de suportul de deschidere (opening bracket).
Folosiți două spații de indentare.
Utilizați punct și virgulă după fiecare pereche proprietate-valoare, inclusiv ultima.
Utilizați ghilimele în jurul valorilor numai dacă valoarea conține spații.
Plasați suportul de închidere (opening bracket) pe o linie nouă, fără spații de conducere.
Evitați liniile de peste 80 de caractere.
Se încarcă JavaScript în HTML
Accesarea elementelor HTML cu JavaScript
Utilizați numele de fișiere scrise cu litere mici
Fișierele HTML ar trebui să aibă o extensie .html sau .htm.
Fișierele CSS ar trebui să aibă o extensie .css.
Fișierele JavaScript ar trebui să aibă o extensie .js.
Nu există nicio diferență între extensiile .htm și .html. Ambele vor fi tratate ca HTML de orice browser web sau server web.
Când o adresă URL nu specifică un nume de fișier (cum ar fi https://www.lectii-virtuale.ro/css/), serverul returnează un nume de fișier implicit. Numele de fișiere implicite obișnuite sunt index.html, index.htm, default.html și default.htm.
Dacă serverul dvs. este configurat doar cu "index.html" ca nume de fișier implicit, fișierul dvs. trebuie numit "index.html", nu "index.htm."
Grafică HTML
Pentru a desena grafică pe o pagină web este utilizat elementul HTML <canvas> .
Elementul HTML <canvas> este utilizat pentru a desena grafică, din nou, prin JavaScript.
Elementul <canvas> este doar un container pentru grafică. Pentru a desena grafică trebuie să utilizați JavaScript.
Canvas are mai multe metode pentru a desena căi, cutii, cercuri, text și adăugarea de imagini.
Specificați întotdeauna un atribut id (la care se face referire într-un script) și un atribut lățime și înălțime (width și height) pentru a defini dimensiunea pânzei (canvas). Pentru a adăuga un chenar (border), utilizați atributul stil (style).
HTML SVG
SVG înseamnă grafică vectorială scalabilă.
SVG este utilizat pentru a defini grafica pentru Web.
SVG este o recomandare W3C.
Elementul HTML <svg> este un container pentru grafică SVG.
SVG are mai multe metode pentru desenarea căilor, casetelor, cercurilor, textului și imaginilor grafice.
Diferențele dintre SVG și Canvas
SVG este un limbaj pentru descrierea graficelor 2D în XML.
Canvas desenează grafică 2D, pe fugă (cu un JavaScript).
SVG este bazat pe XML, ceea ce înseamnă că fiecare element este disponibil în DOM SVG. Puteți atașa manipulatoare de evenimente JavaScript (JavaScript event handlers) pentru un element.
În SVG, fiecare formă desenată este amintită ca obiect. Dacă se schimbă atributele unui obiect SVG, browserul poate reda automat forma.
Canvas: Rezoluție dependentă. Fără suport pentru organizatorii de evenimente.Capacități slabe de redare a textului. Puteți salva imaginea rezultată ca .png sau .jpg. Bine potrivit pentru jocuri cu intensitate grafică.
SVG: Rezoluție independentă. Suport pentru operatorii de evenimente. Cel mai potrivit pentru aplicații cu zone de redare mari (Google Maps). Redarea lentă, dacă este complexă (orice lucru care utilizează mult DOM va fi lent). Nu este potrivit pentru aplicații de joc.
HTML Media
Multimedia pe web inseamnă sunet, muzică, videoclipuri, filme și animații.
Exemple: imagini, muzică, sunet, videoclipuri, înregistrări, filme, animații și multe altele.
Paginile web conțin adesea elemente multimedia de diferite tipuri și formate.
Primele browsere web au avut suport doar pentru text, limitat la un singur font într-o singură culoare.
Mai târziu au venit browserele cu suport pentru culori și fonturi și imagini!
Formatele audio, video și animație au fost gestionate diferit de majoritatea browserelor. Diferite formate au fost acceptate, iar unele formate necesită programe auxiliare suplimentare (plug-in-uri) pentru a funcționa.
Sperăm că acest lucru va deveni istorie. Multimedia HTML5 promite un viitor mai ușor pentru multimedia.
Elementele multimedia (cum ar fi audio sau video) sunt stocate în fișiere media.
Cea mai obișnuită modalitate de a descoperi tipul de fișier este de a privi extensia de fișier.
Fișierele multimedia au formate și extensii diferite precum: .swf, .wav, .mp3, .mp4, .mpg, .wmv și .avi.
MP4 este noul și următorul format pentru video pe internet.
MP4 este recomandat de YouTube.
MP4 este acceptat de Flash Players.
MP4 este acceptat de HTML5.
Doar videoclipurile MP4, WebM și Ogg sunt acceptate de standardul HTML5.
MP3 este cel mai nou format pentru muzică înregistrată comprimat. Termenul MP3 a devenit sinonim cu muzica digitală.
Dacă site-ul dvs. web este despre muzică înregistrată, MP3 este alegerea.
Doar MP3, WAV și Ogg audio sunt acceptate de standardul HTML5.
HTML5 Video
Redarea videoclipurilor în HTML
Înainte de HTML5, un videoclip putea fi redat doar într-un browser cu un plug-in (precum flash).
Elementul HTML5 <video> specifică un mod standard de a încorpora un videoclip într-o pagină web.
Pentru a afișa un videoclip în HTML, utilizați elementul <video>.
Atributul de control (controls) adaugă controale video, cum ar fi: redare, pauză și volum.
Este o idee bună să includeți întotdeauna atributele de lățime și înălțime (width și height). Dacă nu sunt setate înălțimea și lățimea (width și height), pagina ar putea clipi în timp ce video-ul se încarcă.
Elementul <source> vă permite să specificați fișiere video alternative din care browserul poate alege. Browserul va folosi primul format recunoscut.
Textul dintre etichetele <video> și </video> va fi afișat numai în browserele care nu acceptă elementul <video>.
Pentru a începe un videoclip automat, utilizați atributul autoplay.
Atributul de redare automată (autoplay) nu funcționează pe dispozitive mobile precum iPad și iPhone.
În HTML5, există 3 formate video acceptate: MP4, WebM și Ogg.
HTML5 definește metodele, proprietățile și evenimentele DOM pentru elementul <video>.
Acest lucru vă permite să încărcați, să redați și să întrerupeți videoclipuri, precum și să setați durata și volumul.
<video> Definește un videoclip sau un film
<source> Definește mai multe resurse media pentru elemente media, cum ar fi <video> și <audio>
<track> Definește piesele text în playerele media
HTML5 Audio
Înainte de HTML5, fișierele audio puteau fi redate doar într-un browser cu un plug-in (cum ar fi flash).
Elementul HTML5 <audio> specifică un mod standard de a încorpora un audio într-o pagină web.
Pentru a reda un fișier audio în HTML, utilizați elementul <audio>:
Atributul de control (controls) adaugă controale audio, cum ar fi redare, pauză și volum.
Elementul <source> vă permite să specificați fișiere audio alternative din care browserul poate alege. Browserul va folosi primul format recunoscut.
Textul dintre etichetele <audio> și </audio> va fi afișat numai în browserele care nu acceptă elementul <audio>.
În HTML5, există 3 formate audio acceptate: MP3, WAV și OGG.
HTML5 definește metodele, proprietățile și evenimentele DOM pentru elementul <audio>.
Acest lucru vă permite să încărcați, să redați și să întrerupeți un fișier audio, precum și să setați durata și volumul.
Există, de asemenea, evenimente DOM care vă pot notifica atunci când un audio începe să se redea, este în pauză etc.
<source> - Definește multiple resurse media pentru elemente media, cum ar fi video și audio.
HTML Plug-ins
Scopul unui plug-in este extinderea funcționalității unui browser web.
Aplicațiile Helper (plug-in-uri) sunt programe de calculator care extind funcționalitatea standard a unui browser web.
Exemple de plug-in-uri cunoscute sunt applet-urile Java.
Plug-in-urile pot fi adăugate la paginile web cu eticheta <object> sau cu eticheta<embed>.
Plug-in-urile pot fi utilizate în mai multe scopuri: afișarea hărților, scanarea virușilor, verificarea codului dvs. bancar etc.
Pentru a afișa videoclipuri și audio: utilizați etichetele <video> și <audio>.
Elementul <object> este acceptat de toate browserele.
Elementul <object> definește un obiect încorporat într-un document HTML.
Este utilizat pentru a încorpora plug-in-uri (cum ar fi applet-uri Java, cititoare PDF, Flash Players) în paginile web.
Elementul <object> poate fi de asemenea utilizat pentru a include HTML în HTML sau imagini.
Elementul <embed> este acceptat în toate browserele principale.
Elementul <embed> definește, de asemenea, un obiect încorporat într-un document HTML.
Navigatoarele web au acceptat elementul <embed> de mai mult timp. Cu toate acestea, nu a făcut parte din specificația HTML înainte de HTML5.
Elementul <embed> nu are o etichetă de închidere. Nu poate conține text alternativ.
Elementul <embed> poate fi folosit și pentru a include HTML în HTML sau imagini.
HTML YouTube
Cel mai simplu mod de a reda videoclipuri în HTML, este să folosiți YouTube.
Conversia videoclipurilor în diferite formate poate fi dificilă și necesită mult timp.
O soluție mai ușoară este să permiteți YouTube-ului să redea videoclipurile din pagina dvs. web.
YouTube va afișa un id (cum ar fi tgbNymZ7vqY), atunci când salvați (sau redați) un videoclip.
Puteți utiliza acest id și faceți referire la videoclipul dvs. în codul HTML.
Pentru a reda videoclipul dvs. pe o pagină web, faceți următoarele:
Încărcați videoclipul pe YouTube Ia o notă de identificare a videoclipului.
Definiți un element <frame> în pagina dvs. web.
Lăsați atributul src să indice URL-ul videoclipului.
Utilizați atributele de lățime și înălțime (width și height) pentru a specifica dimensiunea playerului.
Adăugați alți parametri la adresa URL (vezi mai jos).
Redare automată YouTube (YouTube Autoplay)
Puteți face ca videoclipul dvs. să înceapă să se redea automat atunci când un utilizator vizitează pagina respectivă adăugând un parametru simplu la adresa URL a YouTube.
Fiți atenți când decideți redarea automată a videoclipurilor dvs. Pornirea automată a unui videoclip vă poate enerva vizitatorul și poate ajunge să provoace mai mult rău decât bine.
Listă de redare YouTube (YouTube Playlist)
O listă separată de virgule a videoclipurilor de redat (pe lângă adresa URL originală).
Buclă YouTube (YouTube Loop)
Valoarea 0 (implicit): Videoclipul va fi redat o singură dată.
Valoarea 1: Videoclipul se va bucla (pentru totdeauna).
Controale YouTube (YouTube Controls)
Valoarea 0: Player controls nu se afișează.
Valoarea 1 (implicit): Afișare player controls.
YouTube - Folosim <object> sau <embed>
YouTube <object> și <embed> sunt depășite din ianuarie 2015. Ar trebui să vă migrați videoclipurile pentru a utiliza <iframe>.
HTML APIs
API Geolocalizare HTML este utilizat pentru a localiza poziția unui utilizator.
Localizați Poziția Utilizatorului
API Geolocalizare în HTML este utilizat pentru a obține poziția geografică a unui utilizator.
Deoarece acest lucru poate compromite confidențialitatea, poziția nu este disponibilă decât dacă utilizatorul o aprobă.
Geolocalizarea este cea mai precisă pentru dispozitivele cu GPS, cum ar fi smartphone-ul.
Începând cu Chrome 5.0, API-ul de geolocalizare va funcționa numai pe contexte sigure, cum ar fi HTTPS. Dacă site-ul dvs. este găzduit pe o origine nesigură (cum ar fi HTTP), solicitările pentru a obține locația utilizatorilor nu vor mai funcționa.
Utilizarea geolocalizării în HTML
Metoda getCurrentPosition () este utilizată pentru a returna poziția utilizatorului.
Al doilea parametru al metodei getCurrentPosition () este utilizat pentru a gestiona erorile. Specifică o funcție care trebuie executată dacă nu reușește să obțină locația utilizatorului:
Pentru a afișa rezultatul într-o hartă, aveți nevoie de acces la un serviciu de hartă, cum ar fi Google Maps.
Geolocalizarea este de asemenea foarte utilă pentru informații specifice locației, cum ar fi:
Informații locale actualizate.
Afișare Puncte de interes în apropierea utilizatorului.
Navigare rotativă (GPS).
Metoda getCurrentPosition () returnează un obiect de succes. Proprietățile de latitudine, longitudine și precizie sunt întotdeauna returnate. Celelalte proprietăți sunt returnate dacă sunt disponibile:
coords.latitude - Latitudinea ca număr zecimal (întors întotdeauna)
coords.longitude - Longitudinea ca număr zecimal (întors întotdeauna)
coords.acuratetă - Precizia poziției (întoarsă întotdeauna)
coords.altitude - Altitudinea în metri peste nivelul mării medii (returnat dacă este disponibil)
coords.altitude - Accarity Precizia altitudinii de poziție (returnată dacă este disponibilă)
coords.heading - Titlul ca grade în sensul acelor de ceasornic dinspre nord (returnat dacă este disponibil)
coords.speed - Viteza în metri pe secundă (returnată dacă este disponibilă)
timestamp - Data / ora răspunsului (returnat dacă este disponibil)
Obiect de geolocalizare - Alte metode interesante
watchPosition () - returnează poziția actuală a utilizatorului și continuă să returneze poziția actualizată pe măsură ce utilizatorul se mișcă (precum GPS-ul într-o mașină).
clearWatch () - Oprește metoda watchPosition ().
HTML5 Drag and Drop
Drag and drop este o caracteristică foarte comună. Este atunci când „apucați” un obiect și îl trageți într-o altă locație.
În HTML5, drag and drop face parte din standard: Orice element poate fi tras.
Pentru a face un element care poate fi trasat, setați atributul dragable pe true
Atributul ondragstart apelează o funcție, drag (eveniment), care specifică ce date trebuie să fie trasate.
Metoda dataTransfer.setData () stabilește tipul de date și valoarea datelor trase.
Evenimentul ondragover specifică unde pot fi eliminate datele trase.
În mod implicit, datele / elementele nu pot fi abandonate în alte elemente. Pentru a permite o eliminare, trebuie să prevenim manipularea implicită a elementului.
Acest lucru se realizează prin apelarea metodei event.preventDefault () pentru evenimentul ondragover.
Atunci când datele glisate sunt abandonate, apare un eveniment drop.
Atributul ondrop apelează o funcție, drop(eveniment).
Call preventDefault() - pentru a preveni gestionarea implicită a datelor browserului (implicit este deschis ca link in drop)
Obțineți datele trase cu metoda dataTransfer.getData (). Această metodă va returna orice date care au fost setate la același tip în metoda setData()
Datele trase sunt id-ul elementului tras ("drag1")
Adăugați elementul tras în elementul drop.
Stocare Web în HTML5
Stocare web în HTML - mai bine decât cookie-urile.
Cu stocarea web, aplicațiile web pot stoca datele local în browserul utilizatorului.
Stocarea web este mai sigură și cantități mari de date pot fi stocate local, fără a afecta performanța site-ului web.
Spre deosebire de cookie-uri, limita de stocare este mult mai mare (cel puțin 5 MB) și informațiile nu sunt transferate niciodată pe server.
Stocarea web este pe origine (pe domeniu și protocol). Toate paginile, de la o origine, pot stoca și accesa aceleași date.
Obiecte de stocare Web în HTML
Stocarea web în HTML furnizează două obiecte pentru stocarea datelor pe client:
window.localStorage - stochează date fără dată de expirare.
window.sessionStorage - stochează datele pentru o sesiune (datele se pierd la închiderea filei browserului).
Înainte de a utiliza stocarea web, verificați asistența browserului pentru localStorage și sessionStorage.
Obiectul localStorage stochează datele fără data de expirare. Datele nu vor fi șterse atunci când browserul este închis și vor fi disponibile a doua zi, săptămână sau an.
Perechile nume / valoare sunt întotdeauna stocate ca șiruri. Nu uitați să le convertiți în alt format atunci când este nevoie!
Obiectul sessionStorage este egal cu obiectul localStorage, cu excepția faptului că stochează datele pentru o singură sesiune. Datele sunt șterse atunci când utilizatorul închide fila browserului specific.
HTML5 Web Workers
Un lucrător web este un JavaScript care rulează în fundal, fără a afecta performanța paginii.
Când executați scripturi într-o pagină HTML, pagina nu răspunde până la finalizarea scriptului.
Un lucrător web (web worker) este un JavaScript care rulează în fundal, independent de alte scripturi, fără a afecta performanța paginii. Puteți continua să faceți orice doriți: făcând click, selectând lucruri etc., în timp ce lucrătorul web (web worker) rulează în fundal.
Înainte de a crea un lucrător web (web worker), verificați dacă browserul utilizatorului îl acceptă.
Creați un fișier Web Worker.
Creăm lucrătorul nostru web (web worker) într-un JavaScript extern.
Creem un script care contează. Scriptul este stocat în fișierul "demo_workers.js".
Apoi putem trimite și primi mesaje de la lucrătorul web (web worker).
Adăugați un ascultător de eveniment „onmessage” la lucrătorul web (web worker).
Când lucrătorul web (web worker) postează un mesaj, codul din ascultătorul evenimentului este executat. Datele de la lucrătorul web (web worker) sunt stocate în event.data.
Încheiați un lucrător web (web worker).
Când se creează un obiect de lucru web(web worker), acesta va continua să asculte mesajele (chiar și după terminarea scriptului extern) până la încheierea acestuia.
Pentru a încheia un lucrător web (web worker) și a resurselor gratuite pentru browser / computer, utilizați metoda terminare ().
Reutilizați Web Worker.
Dacă setați variabila lucrător (worker) pe nedeterminată, după terminarea acesteia, puteți refolosi codul.
Întrucât lucrătorii web (web workers) se află în fișiere externe, aceștia nu au acces la următoarele obiecte JavaScript:
Obiectul ferestrei.
Obiectul documentului.
Obiectul părinte.
Evenimente trimise de server în HTML5
Evenimentele trimise de server permit unei pagini web să primească actualizări de la un server.
Evenimente trimise de server - mesagerie unidirecțională.
Un eveniment trimis de server este atunci când o pagină web primește automat actualizări de la un server.
Acest lucru era posibil și înainte, dar pagina web ar trebui să întrebe dacă există actualizări disponibile. Cu evenimente trimise de server, actualizările vin automat.
Obiectul EventSource este utilizat pentru a primi notificări de evenimente trimise de server.
Creați un nou obiect EventSource și specificați adresa URL a paginii care trimite actualizările (în acest exemplu "demo_sse.php").
De fiecare dată când se primește o actualizare, apare evenimentul onmessage.
Când are loc un eveniment onmessage, introduceți datele primite în elementul cu id = "result".
Verificați asistența pentru evenimente trimise de server
Aveți nevoie de un server capabil să trimită actualizări de date (cum ar fi PHP sau ASP).
Sintaxa fluxului de evenimente din partea serverului este simplă. Setați antetul „Content-Type” la „text / stream-event”. Acum puteți începe să trimiteți fluxuri de evenimente.
Setați antetul „Content-Type” la „text / stream-event”.
Specificați că pagina nu ar trebui să fie în cache.
Afișați datele care trebuie trimise (începeți întotdeauna cu „date:”).
Curățați datele de ieșire înapoi pe pagina web.
Evenimentul onmessage pentru a primi mesaje.
Alte evenimente:
onopen - Când se deschide o conexiune la server.
onmessage - Când un mesaj este primit.
onerror - Când apare o eroare.
CSS Introducere
CSS este un limbaj care descrie stilul unui document HTML.
CSS descrie modul în care trebuie afișate elementele HTML.
CSS reprezintă Cascading Style Sheets.
CSS descrie modul în care elementele HTML trebuie să fie afișate pe ecran, pe hârtie sau în alte suporturi.
CSS economisește multă muncă. Poate controla aspectul mai multor pagini web simultan.
Fișele de stil externe (external stylesheets) sunt stocate în fișiere CSS.
CSS este utilizat pentru a defini stiluri pentru paginile dvs. web, inclusiv designul, aspectul și variațiile de afișare pentru diferite dispozitive și dimensiuni de ecran.
HTML nu a fost niciodată destinat să conțină etichete pentru formatarea unei pagini web!
HTML a fost creat pentru a descrie conținutul unei pagini web.
Când etichete ca <font> și atribute de culoare au fost adăugate la specificația HTML 3.2, a început un coșmar pentru dezvoltatorii web. Dezvoltarea de site-uri web mari, unde fonturile și informațiile despre culoare erau adăugate la fiecare pagină, a devenit un proces lung și scump.
Pentru a rezolva această problemă, World Wide Web Consortium (W3C) a creat CSS.
Definițiile de stil sunt salvate în mod normal în fișiere .css externe.
Cu un fișier de foi de stil externe (external stylesheet file), puteți schimba aspectul unui întreg site web schimbând doar un singur fișier!
CSS Sintaxă
Un set de reguli CSS constă dintr-un selector și un bloc de declarații.
Selectorul indică elementul HTML pe care doriți să-l creeze în stil.
Blocul de declarație conține una sau mai multe declarații separate prin punct și virgulă.
Fiecare declarație include un nume de proprietate CSS și o valoare, separate de două puncte.
O declarație CSS se încheie întotdeauna cu punct și virgulă, iar blocurile de declarație sunt înconjurate de acolade.
Comentariile sunt utilizate pentru a explica codul și pot fi utile atunci când editați codul sursă la o dată ulterioară.
Comentariile sunt ignorate de browsere.
Un comentariu CSS începe cu / * și se termină cu * /. De asemenea, comentariile pot cuprinde mai multe linii.
CSS Selectori
Selectoarele CSS sunt utilizate pentru a „găsi” (sau a selecta) elementele HTML pe care doriți să le modelați.
Putem împărți selectorii CSS în cinci categorii:
Selectoare simple (selectează elemente bazate pe nume, id, clasă)
Selectoare combinate (elemente selectate bazate pe o relație specifică între ele)
Selectori de clasă pseudo (elemente selectate bazate pe o anumită stare)
Selectoare pseudo-elemente (selectează și stilează o parte dintr-un element)
Selectori de atribute (elemente selectate bazate pe un atribut sau o valoare de atribut)
Această pagină va explica cei mai de bază selectori CSS.
Selectorul de elemente selectează elemente HTML pe baza numelui elementului.
Selectorul id utilizează atributul id al unui element HTML pentru a selecta un anumit element.
ID-ul unui element este unic într-o pagină, astfel încât selectorul de id este utilizat pentru a selecta un element unic!
Pentru a selecta un element cu un anumit id, scrieți un caracter hash (#), urmat de id-ul elementului.
Selectorul CSS class
Selectorul de clase (class) selectează elemente HTML cu un atribut de clasă specific.
Pentru a selecta elemente cu o anumită clasă, scrieți un caracter (.), urmat de numele clasei.
Puteți specifica, de asemenea, că numai anumite elemente HTML ar trebui să fie afectate de o clasă.
Elementele HTML se pot referi, de asemenea, la mai multe clase.
Elementul <p> va fi stilat în funcție de class = "center" și de class = "large".
Numai elementele <p> cu class = "center" vor fi aliniate la centru (center-aligned).
Un nume de clasă nu poate începe cu un număr!
Selectorul universal CSS
Selectorul universal (*) selectează toate elementele HTML din pagină.
Selectorul de grupare CSS
Selectorul de grupare selectează toate elementele HTML cu aceleași definiții de stil.
.class .intro - Selectează toate elementele cu class = "intro".
#id #firstname - Selectează elementul cu id = "firstname".
* - Selectează toate elementele.
element p - Selectează toate elementele <p>.
element, element, .. div, p - Selectează toate elementele <div> și toate elementele <p>.
Cum să adăugați CSS
Când un browser citește o foaie de stil, acesta va format documentul HTML în conformitate cu informațiile din foaia de stil.
Trei modalități de a insera CSS.
Există trei moduri de inserare a unei foi de stil:
CSS extern
CSS intern
CSS inline
CSS extern
Cu o foaie de stil extern, puteți schimba aspectul unui întreg site web schimbând doar un singur fișier!
Fiecare pagină HTML trebuie să includă o trimitere la fișierul de stil extern din interiorul elementului <link>, în secțiunea head.
Stilurile externe sunt definite în elementul <link>, în secțiunea <head> a unei pagini HTML.
O foaie de stil extern poate fi scrisă în orice editor de text și trebuie salvată cu o extensie .css.
Fișierul .css extern nu trebuie să conțină nicio etichetă HTML.
Nu adăugați un spațiu între valoarea proprietății și unitate (cum ar fi margin-left: 20 px;). Modul corect este: margin-left: 20px;
CSS intern
Poate fi utilizată o foaie de stil internă (internal style sheet) dacă o singură pagină HTML are un stil unic.
Stilul intern este definit în elementul <style>, în interiorul secțiunii head.
CSS inline
Se poate folosi un stil inline pentru a aplica un stil unic pentru un singur element.
Pentru a utiliza stiluri în linie, adăugați atributul stylela elementul relevant. Atributul de stil poate conține orice proprietate CSS.
Stilurile în linie sunt definite în atributul „style ” al elementului relevant.
Fișe de stil multiple (Multiple Style Sheets)
Dacă unele proprietăți au fost definite pentru același selector (element) în foi de stil diferite, se va utiliza valoarea din ultima foaie de stil citită.
Comandă în cascadă
Toate stilurile dintr-o pagină se vor „încadra” într-o nouă foaie de stil „virtuală” după următoarele reguli, unde numărul unu are cea mai mare prioritate:
Stil în linie (în interiorul unui element HTML).
Fișe de stil externe și interne (în secțiunea cap).
Setare implicită a browserului.
Deci, un stil inline are cea mai mare prioritate și va înlocui stilurile externe și interne și valorile implicite ale browserului.
Culori CSS
Culorile sunt specificate folosind nume de culori predefinite sau valori RGB, HEX, HSL, RGBA, HSLA.
Nume de culoare CSS.
În CSS, o culoare poate fi specificată folosind un nume de culoare.
CSS / HTML acceptă 140 de nume standard de culori.
Culoare de fundal CSS (CSS Background Color).
Puteți seta culoarea de fundal pentru elementele HTML.
Culoare text CSS (CSS Text Color).
Puteți seta culoarea textului.
Culoarea marginilor în CSS (CSS Border Color).
Puteți seta culoarea marginilor.
Valori de culoare CSS (CSS Color Values).
În CSS, culorile pot fi de asemenea specificate folosind valori RGB, valori HEX, valori HSL, valori RGBA și valori HSLA.
Valoarea CSS RGB
În CSS, o culoare poate fi specificată ca valoare RGB, folosind această formulă:
rgb (roșu, verde, albastru) / rgb(red, green, blue)
Fiecare parametru (roșu, verde și albastru)/rgb(red, green, blue) definește intensitatea culorii între 0 și 255.
De exemplu, rgb (255, 0, 0) este afișat ca roșu, deoarece roșul este setat la valoarea cea mai mare (255), iar celelalte sunt setate pe 0.
Pentru a afișa culoarea neagră, toți parametrii de culoare trebuie să fie setați la 0, astfel: rgb (0, 0, 0).
Pentru a afișa culoarea albă, toți parametrii de culoare trebuie să fie setați la 255, astfel: rgb (255, 255, 255).
Valoarea CSS HEX
În CSS, o culoare poate fi specificată folosind o valoare hexadecimală sub forma:
#rrggbb
În cazul în care rr (roșu), gg (verde) și bb (albastru) sunt valori hexadecimale între 00 și ff (la fel ca zecimale 0-255).
De exemplu, # ff0000 este afișat ca roșu, deoarece roșul este setat la cea mai mare valoare (ff), iar celelalte sunt setate la cea mai mică valoare (00).
Valoare HSL.
În CSS, o culoare poate fi specificată folosind nuanță, saturație și ușurință (HSL) sub forma:
hsl (nuanță, saturație, ușurință)/ hsl (hue, saturation, lightness).
Hue este un grad pe roata de culoare de la 0 la 360. 0 este roșu, 120 este verde și 240 albastru.
Saturația este o valoare procentuală, 0% înseamnă o nuanță de gri, iar 100% este culoarea completă.
De asemenea, lumina este procentuală, 0% este negru, 50% nu este nici lumină, nici întunecată, 100% alb.
Saturația (saturation).
Saturația poate fi descrisă ca intensitatea unei culori.
100% este de culoare pură, fără nuanțe de gri
50% este 50% gri, dar puteți vedea în continuare culoarea.
0% este complet gri, nu mai puteți vedea culoarea.
Luminozitate (Lightness).
Luminozitatea unei culori poate fi descrisă cât de multă lumină doriți să dați culorii, unde 0% nu înseamnă lumină (negru), 50% înseamnă 50% lumină (nici întuneric, nici lumină) 100% înseamnă lumină completă (alb).
Nuanțele de gri sunt adesea definite prin setarea nuanței și a saturației la 0 și reglați luminozitatea de la 0% la 100% pentru a obține nuanțe mai închise / mai deschise.
Valoarea RGBA.
Valorile de culoare RGBA sunt o extensie a valorilor de culoare RGB cu un canal alfa - care specifică opacitatea unei culori.
O valoare de culoare RGBA este specificată cu:
rgba (roșu, verde, albastru, alfa) / rgba(red, green, blue, alpha)
Parametrul alfa este un număr între 0.0 (complet transparent) și 1.0 (deloc transparent).
Valoarea HSLA.
Valorile de culoare HSLA sunt o extensie a valorilor de culoare HSL cu un canal alfa - care specifică opacitatea unei culori.
O valoare de culoare HSLA este specificată cu:
hsla (nuanță, saturație, luminozitate, alfa) / hsla (hue, saturation, lightness, alpha)
Parametrul alfa este un număr între 0.0 (complet transparent) și 1.0 (deloc transparent).
CSS Fundaluri
Proprietățile de fundal CSS sunt utilizate pentru a defini efectele de fundal pentru elemente.
Proprietăți de fundal CSS: culoare de fundal, imagine de fundal, fundal repetare, background-attachment, background-position.
Culoare de fundal CSS ( CSS background-color).
Proprietatea de culoare de fundal specifică culoarea de fundal a unui element.
Cu CSS, o culoare este cel mai des specificată de: un nume de culoare valid - precum „roșu”, o valoare HEX - ca „# ff0000”, o valoare RGB - ca „rgb (255,0,0)”.
Imagine de fundal CSS (CSS background-image)
Proprietatea de fundal imagine specifică o imagine pe care să o folosească ca fundal al unui element.
În mod implicit, imaginea este repetată, astfel încât acoperă întregul element.
Când utilizați o imagine de fundal, utilizați o imagine care nu perturba textul.
Repetare de fundal CSS (CSS background-repeat)
În mod implicit, proprietatea imaginii de fundal repetă o imagine atât pe orizontală cât și pe verticală.
Unele imagini trebuie repetate doar pe orizontală sau vertical sau vor arăta ciudat, astfel:
Pentru a repeta o imagine pe verticală, setați background-repeat: repeat-y;
Fundal CSS-repetare: nu se repetă (CSS background-repeat: no-repeat)
Afișarea imaginii de fundal o singură dată este, de asemenea, specificată de proprietatea background-repeat.
În exemplul de mai sus, imaginea de fundal este plasată în același loc cu textul. Vrem să schimbăm poziția imaginii, astfel încât să nu deranjeze prea mult textul.
Poziția de fundal CSS (CSS background-position).
Proprietatea poziție fundal este utilizată pentru a specifica poziția imaginii de fundal.
Atasament de fundal CSS (CSS background-attachment).
Proprietatea de atașare de fundal specifică dacă imaginea de fundal trebuie să se deruleze sau să fie fixată (nu va defila cu restul paginii).
Fundal CSS - proprietatea shorthand
Pentru a scurta codul, este de asemenea posibil să specificați toate proprietățile de fundal într-o singură proprietate. Aceasta se numește o proprietate shorthand.
Proprietatea shorthand pentru fundal este fundal.
Când folosiți proprietatea shorthand ordinea valorilor proprietății este:
background-color
background-image
background-repeat
background-attachment
background-position
Nu contează dacă lipsește una din valorile proprietății, atât timp cât celelalte sunt în această ordine.
background - Setează toate proprietățile fundalului într-o singură declarație
background-attachment - Setează dacă o imagine de fundal este fixă sau defilează cu restul paginii
background-clip - Specifică zona de pictură a fundalului
background-color - Setează culoarea de fundal a unui element
background-image - Setează imaginea de fundal pentru un element
background-origin - Specifică unde este / sunt poziționate imaginile de fundal
background-position - Setează poziția de pornire a unei imagini de fundal
background-repeat - Setează modul în care se va repeta o imagine de fundal
background-size - Specifică dimensiunea imaginii de fundal
CSS Borders
Proprietăți CSS Borders.
Proprietățiile CSS Borders vă permit să specificați stilul, lățimea și culoarea chenarului unui element.
CSS Border Style.
Proprietatea CSS Border Style specifică ce fel de chenar trebuie afișat.
Sunt permise următoarele valori:
dotted (punctat) - Definește un chenar (border) punctat.
dashed - Definește o bordură (border) punctată.
solid - Definește o bordură (border) solidă.
double (dublu) - Definește o bordură (border) dublă.
groove - Definește un chenar cu caneluri 3D. Efectul depinde de valoarea culorii bordurii (border-color).
ridge - Definește un chenar (border) ridicat 3D. Efectul depinde de valoarea culorii bordurii (border-color).
inset - Definește un chenar (border) de inserție 3D. Efectul depinde de valoarea culorii bordurii (border-color).
outset - Definește un chenar (border) de declanșare 3D. Efectul depinde de valoarea culorii bordurii (border-color).
none - Nu definește nici o frontieră (border).
hidden (ascuns) - definește un chenar (border) ascuns.
Proprietatea border-style poate avea de la una până la patru valori (pentru top border, right border, bottom border, left border).
Niciuna dintre celelalte proprietăți CSS border descrise mai jos nu va avea NICIUN efect, decât dacă este setată proprietatea border-style!
Lățimea marginilor CSS (CSS Border Width)
Proprietatea border-width specifică lățimea celor patru chenare.
Lățimea poate fi setată ca o dimensiune specifică (în px, pt, cm, em, etc.) sau folosind una dintre cele trei valori predefinite: subțire, medie sau groasă (thin, medium, thick.).
Proprietatea border-width poate avea de la una până la patru valori (pentru marginea superioară, granița dreaptă, limita de jos și marginea din stânga/ top border, right border, bottom border, left border).
CSS Border Color
Proprietatea border-color este utilizată pentru a seta culoarea celor patru chenare.
Culoarea poate fi setată de:
name - Specificați un nume de culoare, cum ar fi „red”.
Hex - Specificați o valoare hexagonală, cum ar fi „# ff0000”.
RGB - Specificați o valoare RGB, cum ar fi „rgb (255,0,0)”.
transparent.
Proprietatea border-color poate avea de la una până la patru valori (pentru marginea de sus, marginea dreaptă, limita de jos și marginea din stânga/top border, right border, bottom border, left border).Dacă border-color nu este setată, moștenește culoarea elementului.
CSS Border - Individual Sides
Din exemplele de mai sus, ați văzut că este posibil să specificați o frontieră diferită pentru fiecare parte.
În CSS, există, de asemenea, proprietăți pentru specificarea fiecărui chenar (sus, dreapta, jos și stânga/top, right, bottom, left).
Dacă proprietatea border-style are patru valori:
border-style: punctat dublu punctat solid.
top border este punctat.
right border este solid.
bottom border este dublu.
left border este punctat.
Dacă proprietatea border-style are trei valori:border-style: dublu solid punctat.
top border este punctat.
right și left borders sunt solide.
bottom border este dublu.
Dacă proprietatea border-style are două valori:
border-style: solid punctat.
top și bottom borders sunt punctate.
right și left borders sunt solide.
Dacă proprietatea border-style are o valoare:
border-style: punctat.
toate cele patru granițe sunt punctate.
Proprietatea border-style este folosită în exemplul de mai sus. Cu toate acestea, funcționează, de asemenea, cu border-width și border-color.
CSS Border - Proprietatea Shorthand
După cum puteți vedea din exemplele de mai sus, există multe proprietăți de luat în considerare atunci când aveți de-a face cu frontierele.
Pentru a scurta codul, este de asemenea posibil să se specifice toate proprietățile de frontieră individuale într-o singură proprietate.
Proprietatea de frontieră (border) este o proprietate shorthand pentru următoarele proprietăți individuale de frontieră:
border-width
border-style (required)
border-color
Frontierele rotunjite CSS (CSS Rounded Borders).
Proprietatea border-radius este utilizată pentru a adăuga borduri rotunjite la un element.
Toate proprietățile top border într-o singură declarație.
Acest exemplu demonstrează o proprietate shorthand pentru setarea tuturor proprietăților pentru top border într-o singură declarație.
Setați stilul marginii de jos (bottom border).
Acest exemplu demonstrează cum să setați stilul marginii de jos (bottom border).
Setați lățimea marginii din stânga (left border).
Acest exemplu demonstrează modul de setare a lățimii marginii din stânga (left border).
Setați culoarea celor patru chenare (borders).
Acest exemplu demonstrează cum să setați culoarea celor patru chenare. Poate avea de la una la patru culori.
Setați culoarea marginii drepte (right border).
Acest exemplu demonstrează cum să setați culoarea marginii drepte (right border).
border Setează toate proprietățile de frontieră într-o singură declarație
border-bottom Setează toate proprietățile frontierei de jos într-o singură declarație
border-bottom-color Setează culoarea marginii de jos
border-bottom-style Setează stilul marginii de jos
border-bottom-width Setează lățimea marginii de jos
border-color Setează culoarea celor patru chenare
border-left Stabilește toate proprietățile frontierei din stânga într-o singură declarație
border-left-color Setează culoarea marginii din stânga
border-left-style Setează stilul chenarului din stânga
border-left-width Setează lățimea marginii din stânga
border-radius Setează toate cele patru chenare - * - proprietăți ale razei pentru colțurile rotunjite
border-right Setează toate proprietățile de frontieră dreaptă într-o singură declarație
border-right-color Setează culoarea marginii drepte
border-right-style Setează stilul chenarului drept
border-right-width Setează lățimea marginii drepte
border-style Setează stilul celor patru chenare
border-top Setează toate proprietățile de frontieră de sus într-o singură declarație
border-top-color Setează culoarea marginii superioare
border-top-style Setează stilul chenarului superior
border-top-width Setează lățimea marginii superioare
border-width Setează lățimea celor patru chenare
CSS Margini
Proprietățiile CSS margin sunt utilizate pentru a crea spațiu în jurul elementelor, în afara oricărui chenar definit.
Cu CSS, aveți control complet asupra marginilor. Există proprietăți pentru setarea marginii pentru fiecare parte a unui element (sus, dreapta, jos și stânga/top, right, bottom, left).
Margin - Individual Sides
CSS are proprietăți pentru specificarea marginii pentru fiecare parte a unui element: margin-top, margin-right, margin-bottom, margin-left.
Toate proprietățile marginii pot avea următoarele valori:
auto - browserul calculează marginea.
length - specifică o margine în px, pt, cm etc.
% - specifică o margine în% din lățimea elementului care conține.
inherit- specifică faptul că marginea ar trebui să fie moștenită de la elementul părinte. Valorile negative sunt permise.
Setați margini diferite pentru toate cele patru laturi ale unui element <p>.
Pentru a scurta codul, este posibil să specificați toate proprietățile marginii într-o singură proprietate.
Proprietatea margin este o proprietate shorthand pentru următoarele proprietăți margin individuale: margin-top, margin-right, margin-bottom, margin-left.
Dacă proprietatea marjei are patru valori:
margin: 25px 50px 75px 100px;
top margin este 25px
right margin este 50px
bottom margin este 75px
left margin este 100px
Dacă proprietatea margin are trei valori:
margin: 25px 50px 75px;
top margin este de 25px.
right și left margins sunt de 50px.
bottom margin este de 75px.
Dacă proprietatea margin are două valori:
margin: 25px 50px;
top și bottom margins sunt de 25px
right și left margins sunt de 50px
Dacă proprietatea margin are o valoare:
margin: 25px;
toate cele patru margini sunt de 25px
Valoarea auto (The auto Value)
Puteți seta proprietatea marginii ca automat (auto) să centreze orizontal elementul din containerul său.
Elementul va prelua apoi lățimea specificată, iar spațiul rămas va fi împărțit în mod egal între marginile din stânga și cea din dreapta.
Folosiți margin: auto.
Valoarea inherit (The inherit Value).
Acest exemplu permite ca marginea stângă a elementului <p class = "ex1"> să fie moștenită de la elementul părinte (<div>).
Margin Collapse
Marginile superioare și inferioare ale elementelor sunt uneori prăbușite într-o singură margine care este egală cu cea mai mare dintre cele două margini.
Acest lucru nu se întâmplă pe marginile din stânga și din dreapta! Doar marginile de sus și de jos!
Elementul <h1> are marginea de jos de 50px iar elementul <h2> are marginea de sus setată la 20px.
Simțul comun pare să sugereze că marginea verticală dintre <h1> și <h2> ar fi în total 70px (50px + 20px). Dar din cauza colapsului marginii, marginea reală ajunge să fie de 50px.
margin - Proprietate shorthand pentru setarea proprietăților marginii într-o singură declarație.
margin-bottom - Setează marginea de jos a unui element.
margin-left - Setează marginea stângă a unui element.
margin-right - Setează marginea dreaptă a unui element.
margin-top - Setează marginea superioară a unui element.
CSS Padding
Proprietățiile CSS padding sunt utilizate pentru a genera spațiu în jurul conținutului unui element, în interiorul oricărui chenar definit.
Cu CSS, aveți un control complet asupra padding- ului. Există proprietăți pentru setarea padding-ului pentru fiecare parte a unui element (sus, dreapta, jos și stânga/top, right, bottom, left).
Padding - Individual Sides
CSS are proprietăți pentru specificarea padding- ului pentru fiecare parte a unui element: padding-top, padding-right, padding-bottom, padding-left .
Toate proprietățile padding pot avea următoarele valori:
length - Specifică o căptușire în px, pt, cm etc.
% - Specifică un padding în % din lățimea elementului care îl conține.
inherit - Specifică faptul că padding-ul ar trebui să fie moștenit de la elementul părinte.
Valorile negative nu sunt permise.
Padding - Proprietatea Shorthand
Pentru a scurta codul, este posibil să specificați toate proprietățiile padding într-o singură proprietate.
Proprietatea padding este o proprietate shorthand pentru următoarele proprietăți individuale padding: padding-top, padding-right, padding-bottom, padding-left
Dacă proprietatea padding are patru valori:
padding: 25px 50px 75px 100px;
top padding este de 25px
right padding este de 50px
bottom padding este de 75px
left padding este de 100px
Dacă proprietatea padding are trei valori:
padding: 25px 50px 75px;
top padding este de 25px
right și left paddings sunt de 50px
bottom padding este de 75px
Dacă proprietatea padding are două valori:
padding: 25px 50px;
top și bottom paddings sunt de 25px
right și left paddings sunt de 50px
Dacă proprietatea padding are o valoare:
padding: 25px;
toate cele patru garnituri sunt de 25px
Padding și elementul width
Proprietatea CSS width specifică lățimea zonei de conținut a elementului. Zona de conținut este porțiunea din interiorul padding-ului, border și marginea unui element (modelul box).
Deci, dacă un element are o lățime specificată, padding-ul adăugat la acel element va fi adăugat la lățimea totală a elementului. Acesta este adesea un rezultat nedorit.
Pentru a menține lățimea la 300px, indiferent de cantitatea de padding, puteți utiliza proprietatea box-sizing. Acest lucru face ca elementul să-și mențină lățimea; dacă măriți padding-ul, spațiul de conținut disponibil va scădea.
Utilizați proprietatea box-sizing pentru a păstra lățimea la 300px, indiferent de cantitatea de padding.
Setați left padding
Acest exemplu demonstrează modul de setare a left padding-ului unui element <p>.
Setați right padding
Acest exemplu demonstrează cum să setați right padding-ul unui element <p>.
Setați top padding
Acest exemplu demonstrează modul de setare a top padding-ului unui element <p>.
Setați bottom padding
Acest exemplu demonstrează modul de setare a bottom padding-ului unui element <p>.
padding - O proprietate shorthand pentru setarea tuturor proprietăților de umplere într-o singură declarație.
padding-bottom - Setează bottom padding-ul unui element.
padding-left - Stabilește left padding-ul unui element.
padding-right - Setează right padding-ul unui element.
padding-top - Setează top padding-ul unui element.
CSS Height și Width
Proprietățiile height și width sunt utilizate pentru a seta înălțimea și lățimea unui element.
Proprietățiile height și width nu includ padding, borders sau margins. Stabilește înălțimea / lățimea (height/width) zonei din interiorul padding-ului, border-ului și marginii elementului.
Valori CSS înălțime / lățime (height/width)
Proprietățiile de înălțime și lățime (height/width) pot avea următoarele valori:
auto - Aceasta este implicită. Browserul calculează înălțimea și lățimea (height/width).
lenght - Definește înălțimea / lățimea (height/width) în px, cm etc.
% - Definește înălțimea / lățimea (height/width) în procente din blocul conținut.
inițial - Setează înălțimea / lățimea (height/width) la valoarea implicită.
inherit - Înălțimea / lățimea (height/width) vor fi moștenite de la valoarea sa parentală.
Nu uitați că proprietățiile de înălțime și lățime nu includ padding, borders sau margins! Ei setează înălțimea / lățimea zonei din interiorul paddingu-ului, border-ului și marginii elementului!
Setarea lățimii maxime (max-width).
Proprietatea max-width este utilizată pentru a seta lățimea maximă a unui element.
Lățimea maximă (max-width) poate fi specificată în valori de lungime, cum ar fi px, cm, etc., sau în procente (%) din blocul conținut sau setat pe niciunul (acesta este implicit. Înseamnă că nu există o lățime maximă).
Problema cu <div> de mai sus apare atunci când fereastra browserului este mai mică decât lățimea elementului (500px). Browserul apoi adaugă o pagină de defilare orizontală la pagină.
Folosind în schimb această lățime maximă (max-width), în această situație, veți îmbunătăți gestionarea browserului de la ferestrele mici.
Trageți fereastra browserului la o lățime mai mică de 500px, pentru a vedea diferența dintre cele două div-uri!
height - Setează înălțimea unui element.
max-height - Setează înălțimea maximă a unui element.
max-width - Setează lățimea maximă a unui element.
min-height - Setează înălțimea minimă a unui element.
min-width - Setează lățimea minimă a unui element.
width - Setează lățimea unui element.
CSS Box Model
Toate elementele HTML pot fi considerate casete (boxes). În CSS, termenul „model de cutie”(box model) este utilizat atunci când vorbim despre design și aspect.
Modelul CSS box este în esență o cutie care se înfășoară în jurul fiecărui element HTML. Este format din: margini, borders, padding și conținutul real.
Content - Conținutul căsuței, unde apar text și imagini.
Padding - Șterge o zonă din jurul conținutului. Padding este transparent.
Border - O graniță care se întinde pe padding și content.
Margin - Șterge o zonă în afara graniței. Marginea este transparentă
.Modelul casetei (box model) ne permite să adăugăm un chenar în jurul elementelor și să definim spațiul dintre elemente.
Lățimea și înălțimea unui element (Width and Height of an Element).
Pentru a seta corect lățimea și înălțimea (width și height) unui element în toate browserele, trebuie să știți cum funcționează modelul casetei (box model).
CSS Outline
Un outline este o linie care este desenată în jurul elementelor, în afara granițelor (borders), pentru a face ca elementul să „iasă în evidență”.
CSS are următoarele proprietăți outline (contur): outline-style, outline-color, outline-width, outline-offset, outline.
Conturul (outline) diferă de granițe (borders)! Spre deosebire de graniță (border), conturul (outline) este tras în afara graniței elementului și poate suprapune alt conținut. De asemenea, conturul (outline) NU este o parte din dimensiunile elementului; lățimea și înălțimea (height și weight) totală a elementului nu este afectată de lățimea conturului.
CSS Outline Style.
Proprietatea outlyne style specifică stilul conturului și poate avea una dintre următoarele valori:
dotted (punctat) - Definește un contur punctat.
dashed (marcat) - Definește un contur discret.
solid - Definește un contur solid.
double (dublu) - Definește un contur dublu.
groove (canelură) - Definește un contur în canelură 3D.
ridge - Definește un contur 3D ridged.
inset - Definește un contur de inserție 3D.
outset - Definește un contur de declanșare 3D.
none - Nu definește contur.
hidden (ascuns) - Definește un contur ascuns.
Niciuna dintre celelalte proprietăți outline nu va avea niciun efect, cu excepția cazului în care proprietatea în stil outline este setată!
CSS Outline Color.
Proprietatea CSS outline-color este utilizată pentru a seta culoarea conturului.
Culoarea poate fi setată de:
name - Specificați un nume de culoare, cum ar fi „red”.
RGB - Specificați o valoare RGB, cum ar fi „rgb (255,0,0)”.
Hex - Specificați o valoare hexagonală, cum ar fi „# ff0000”.
invert - Realizează o inversare a culorii (care asigură că conturul este vizibil, indiferent de fundalul culorii).
CSS Outline Width.
Proprietatea outline-width specifică lățimea conturului și poate avea una dintre următoarele valori:
thin (subțire) - de obicei 1px.
medium (mediu) - de obicei 3px.
thick (gros) - de obicei 5px.
O dimensiune specifică (în px, pt, cm, em, etc).
CSS Outline - Proprietatea Shorthand
Proprietatea outline este o proprietate shorthand pentru setarea următoarelor proprietăți outline individuale: outline-width, outline-style (required), outline-color.
CSS Outline Offset
Proprietatea outline-offset adaugă spațiu între un outline și edge/ border unui element. Spațiul dintre un element și conturul său este transparent.
Proprietățiile CSS Outline: outline, outline-color, outline-offset, outline-style, outline-width.
outline - O proprietate shorthand pentru setarea contur-lățime, stil contur și contur-culoare într-o singură declarație.
outline-color - Setează culoarea unui contur.
outline-offset - Specifică spațiul dintre un contur și marginea sau marginea unui element.
outline-style - Setează stilul unui contur.
outline-width - Setează lățimea unui contur.
CSS Text
Proprietatea de culoare este utilizată pentru a seta culoarea textului. Culoarea este specificată de:
un nume de culoare - ca „roșu”
o valoare HEX - ca „# ff0000”
o valoare RGB - ca „rgb (255,0,0)”
Consultați CSS Color Values pentru o listă completă a valorilor de culoare posibile.
Culoarea implicită a textului pentru o pagină este definită în selectorul body.
Aliniere text (Text Alignment).
Proprietatea text-align este utilizată pentru a seta alinierea orizontală a unui text.
Un text poate fi aliniat la stânga sau la dreapta, centrat sau justificat (left sau right, centered sau justified).
Când proprietatea de aliniere a textului este „justify”, fiecare linie este întinsă astfel încât fiecare linie să aibă lățimea egală, iar marginile stânga și dreapta sunt drepte (ca în reviste și ziare).
Decorarea textului (Text Decoration).
Proprietatea text-decoration este utilizată pentru a seta sau elimina decorațiunile din text.
Valoarea text-decoration: none; este adesea folosit pentru a elimina sublinierile din link-uri.
Nu este recomandat să subliniați textul care nu este o legătură, deoarece acest lucru încurcă cititorul.
Transformarea textului.
Proprietatea text-transform este utilizată pentru a specifica litere mari și minuscule (uppercase sau lowercase) într-un text.
Poate fi folosit pentru a transforma totul în litere mari sau minuscule (uppercase sau lowercase) sau pentru a valorifica prima literă a fiecărui cuvânt.
Indentare text (Text Indentation).
Proprietatea text-indent este utilizată pentru a specifica indentarea primei linii a unui text.
Spațiul dintre litere (Letter Spacing)
Proprietatea de spațiere a literelor (letter-spacing) este utilizată pentru a specifica spațiul dintre caracterele unui text.
Înălţimea liniei (Line Height).
Proprietatea line-height este utilizată pentru a specifica spațiul dintre linii.
Direcția textului (Text Direction).
Proprietatea direction este utilizată pentru a schimba direcția textului unui element.
Distanțarea cuvintelor (Word Spacing)
Proprietatea word-spacing a cuvintelor este utilizată pentru a specifica spațiul dintre cuvintele dintr-un text.
color - Setează culoarea textului.
direction - Specifică direcția textului / direcția de scriere.
letter-spacing - Crește sau scade spațiul dintre caractere dintr-un text.
line-height - Setează înălțimea liniei.
text-align - Specifică alinierea orizontală a textului.
text-decoration - Specifică decorația adăugată la text.
text-indent - Specifică indentarea primei linii dintr-un bloc de text.
text-shadow - Specifică efectul umbre adăugat textului.
text-transform - Controlează capitalizarea textului.
text-overflow - Specifică modul în care conținutul revărsat care nu este afișat trebuie semnalat utilizatorului.
unicode-bidi - Se folosește împreună cu proprietatea de direcție pentru a seta sau returna dacă textul ar trebui să fie anulat pentru a accepta mai multe limbi din același document.
vertical-align - Setează alinierea verticală a unui element.
white-space - Specifică modul în care este gestionat spațiul alb din interiorul unui element.
word-spacing - Crește sau scade spațiul dintre cuvinte dintr-un text.
CSS Fonturi
Proprietățiile fontului CSS definesc font family, boldness, size și style of a text.
Familii de fonturi CSS (CSS Font Families).
În CSS, există două tipuri de nume de fonturi:
generic family - un grup de familii de fonturi cu aspect similar (cum ar fi „Serif” sau „Monospace”).
font family - o familie de fonturi specifică (cum ar fi „Times New Roman” sau „Arial”).
Font Family.
Familia de fonturi a unui text este setată cu proprietatea font-family.
Proprietatea font-family ar trebui să dețină mai multe nume de font ca sistem „fallback”. Dacă browserul nu acceptă primul font, încearcă următorul font și așa mai departe.
Începeți cu fontul dorit și terminați cu o familie generică (generic family), pentru a permite browserului să aleagă un font similar în familia generică (generic family), dacă nu sunt disponibile alte fonturi.
Dacă numele unei familii de fonturi este mai mult de un cuvânt, acesta trebuie să fie între ghilimele, cum ar fi: „Times New Roman”.
Mai multe familii de fonturi sunt specificate într-o listă separată de virgule.
Stilul fontului (Font Style)
Proprietatea font-style este utilizată mai ales pentru a specifica textul italic.
Această proprietate are trei valori:
normal - Textul este afișat normal.
italic - Textul este afișat cu caractere italice.
oblique - Textul este „aplecat” (oblic este foarte similar cu italic, dar mai puțin susținut).
Proprietatea font-size stabilește dimensiunea textului.
Posibilitatea de a gestiona dimensiunea textului este importantă în proiectarea web. Cu toate acestea, nu ar trebui să utilizați ajustări de dimensiune a fontului pentru a face ca paragrafele să arate ca titluri sau rubricile să pară paragrafe.
Utilizați întotdeauna etichetele HTML adecvate, cum ar fi <h1> - <h6> pentru titluri și <p> pentru paragrafe.
Valoarea font-size poate fi o dimensiune absolută sau relativă.
Dimensiune absolută:
Setează textul la o dimensiune specificată.
Nu permite utilizatorului să modifice dimensiunea textului în toate browserele (greșit din motive de accesibilitate).
Dimensiunea absolută este utilă atunci când dimensiunea fizică a ieșirii este cunoscută.
Mărime relativă:
Setează dimensiunea în raport cu elementele din jur.
Permite unui utilizator să modifice dimensiunea textului în browsere.
Dacă nu specificați o dimensiune a fontului, dimensiunea implicită pentru textul normal, cum ar fi alineatele, este 16px (16px = 1em).
Setarea dimensiunii fontului cu pixeli.
Setarea dimensiunii textului cu pixeli vă oferă un control complet asupra dimensiunii textului.
Dacă utilizați pixeli, puteți utiliza în continuare zoom tool pentru a redimensiona întreaga pagină.
Setați dimensiunea fontului cu Em
Pentru a permite utilizatorilor să redimensioneze textul (în meniul browserului), mulți dezvoltatori folosesc em în loc de pixeli.
Unitatea de dimensiuni em este recomandată de W3C.
1em este egal cu dimensiunea curentă a fontului. Dimensiunea implicită a textului în browsere este 16px. Deci, dimensiunea implicită de 1em este 16px.
Mărimea poate fi calculată de la pixeli la em folosind această formulă: pixeli / 16 = em.
Font Weight
Proprietatea font-weight specifică greutatea unui font:
Responsive Font Size
Mărimea textului poate fi setată cu o unitate vw, ceea ce înseamnă „viewport width”.
Astfel dimensiunea textului va urma dimensiunea ferestrei browserului:
Font Variant
Proprietatea font-variant specifică dacă un text ar trebui să fie afișat sau nu într-un font cu caractere mici.
Într-un font cu caractere mici, toate literele mici sunt convertite în litere mari. Cu toate acestea, literele majuscule convertite apar cu o dimensiune de font mai mică decât literele majuscule originale din text.
font - Setează toate proprietățile fontului într-o singură declarație.
font-family - Specifică familia de fonturi pentru text.
font-size - Specifică dimensiunea fontului textului.
font-style - Specifică stilul de font pentru text.
font-variant - Specifică dacă un text trebuie să fie afișat sau nu într-un font cu caractere mici.
font-weight - Specifică greutatea unui font.
CSS Icons
Cum se adaugă icoane
Cel mai simplu mod de a adăuga o pictogramă pe pagina dvs. HTML, este cu o bibliotecă de pictograme, cum ar fi Font Awesome.
Adăugați numele clasei de pictograme specificate la orice element HTML inline (cum ar fi <i> sau <span>).
Toate pictogramele din bibliotecile cu pictograme de mai jos, sunt vectori scalabili care pot fi personalizați cu CSS (dimensiune, culoare, umbră etc.)
Font Awesome Icons
Pentru a utiliza pictogramele Font Awesome, accesați fontawesome.com, conectați-vă și obțineți un cod pe care să îl adăugați în secțiunea <head> a paginii dvs. HTML:
<script src = "https://kit.fontawesome.com/yourcode.js"> </script>.
Bootstrap Icons.
Pentru a utiliza glificile Bootstrap, adăugați următoarea linie în secțiunea <head> a paginii dvs. HTML:
<link rel = "stylesheet" href = "https://maxcdn.bootstrapcdn.com/bootstrap/3.3.7/css/bootstrap.min.css">.
Bootstrap Icons.
Pentru a utiliza glificile Bootstrap, adăugați următoarea linie în secțiunea <head> a paginii dvs. HTML:
<link rel = "stylesheet" href = "https://maxcdn.bootstrapcdn.com/bootstrap/3.3.7/css/bootstrap.min.css">.
CSS Link-uri
Cu CSS, linkurile pot fi proiectate în moduri diferite.
Styling Links.
Linkurile pot fi realizate cu orice proprietate CSS (de exemplu, culoare, familie de fonturi, fundal etc / color, font-family, background).
În plus, legăturile (linkurile) pot fi proiectate diferit în funcție de starea în care se află.
Cele patru stări de legături (linkuri) sunt:
a: link - o legătură normală, nevăzută.
a:visited - un link pe care l-a vizitat utilizatorul.
a: hover - o legătură atunci când utilizatorul dă peste ea.
a: active - un link în momentul în care este dat click.
Când setați stilul pentru mai multe stări de legătură, există câteva reguli de comandă:
a: hover - TREBUIE să vină după a:link și a:visited.
a: active - TREBUIE să vină după a:hover.
Decorarea textului (Text Decoration).
Proprietatea text-decoration este utilizată mai ales pentru a elimina sublinierile din link-uri.
Culoare de fundal (Background Color)
Proprietatea background-color poate fi utilizată pentru a specifica o culoare de fundal pentru link-uri.
Advanced - Link Buttons.
CSS Liste
În HTML, există două tipuri principale de liste:
liste neordonate (<ul>) - articolele din listă sunt marcate cu buline.
liste ordonate (<ol>) - elementele din listă sunt marcate cu numere sau litere.
Proprietățiile listei CSS vă permit să:
Setați markeri de articole de listă diferite pentru liste ordonate.
Setați markeri de articole de listă diferite pentru liste neordonate.
Setați o imagine ca marker a elementelor din listă.
Adăugați culori de fundal la liste și elemente de listă.
Different List Item Markers
Proprietatea list-style-type specifică tipul markerului de element de listă.
O imagine ca marker element de listă
Proprietatea list-style-image specifică o imagine ca marker al elementului de listă.
Poziționează marcatorii de elemente de listă (Position The List Item Markers)
Proprietatea list-style-position specifică poziția marcatorilor de elemente de listă (puncte glonț).
"list-style-position: outside;" - înseamnă că punctele glonț se vor afla în afara articolului din listă. Începutul fiecărei linii a unui element de listă va fi aliniat vertical. Aceasta este implicită.
"list-style-position: inside;" - înseamnă că punctele glonț vor fi în interiorul articolului din listă. Deoarece face parte din elementul listei, acesta va face parte din text și va împinge textul la început.
Eliminați setările implicite
Proprietatea list-style-type:none poate fi utilizată pentru a elimina markerele / gloanțele. Rețineți că lista are, de asemenea, margin și padding implicite. Pentru a elimina acest lucru, adăugați margin: 0 și padding: 0 până la <ul> sau <ol>.
Listă - Proprietatea Shorthand
Proprietatea list-style este o proprietate de tip shorthand. Este utilizat pentru a seta toate proprietățile listei într-o singură declarație.
Când utilizați proprietatea shorthand, ordinea valorilor proprietății este:
list-style-type - (dacă este specificată o imagine-list-style-image, valoarea acestei proprietăți va fi afișată dacă imaginea din anumite motive nu poate fi afișată)
list-style-position - (specifică dacă markerii elementelor de listă trebuie să apară în interiorul sau în afara fluxului de conținut)
list-style-image (specifică o imagine ca marker pentru elementele de listă)
Dacă una din valorile proprietății de mai sus lipsește, valoarea implicită pentru proprietatea lipsă va fi introdusă, dacă există.
Styling List With Colors.
Putem, de asemenea, stiliza listele cu culori, pentru a le face să pară ceva mai interesante.
Orice lucru adăugat la eticheta <ol> sau <ul>, afectează întreaga listă, în timp ce proprietățile adăugate la eticheta <li> vor afecta elementele listei individuale.
list-style Setează toate proprietățile pentru o listă într-o singură declarație.
list-style-image Specifică o imagine ca marker de listă.
list-style-position Specifică poziția markerilor elementelor din listă (puncte glont).
list-style-type Specifică tipul markerului de listă.
CSS Tabele
Aspectul unui tabel HTML poate fi îmbunătățit mult cu CSS.
Bordurile tabelelor
Pentru a specifica bordurile tabelelor în CSS, utilizați proprietatea border.
Reduceți marginile tabelului (Collapse Table Borders)
Proprietatea border-collapse stabilește dacă bordurile tabelului trebuie să fie prăbușite într-un singur chenar:
Dacă doriți doar un chenar în jurul tabelului, specificați numai proprietatea border pentru <tabel>.
Lățimea și înălțimea tabelului (Table Width and Height)
Lățimea și înălțimea (width și height) unui tabel sunt definite prin proprietățiile de lățime și înălțime.
Aliniere orizontală (Horizontal Alignment)
Proprietatea de aliniere text stabilește alinierea orizontală (cum ar fi stânga, dreapta sau centrul) conținutului în <th> sau <td>.
În mod implicit, conținutul elementelor <th> sunt aliniate în centru și conținutul elementelor <td> sunt aliniate la stânga.
Aliniere verticală (Vertical Alignment)
Proprietatea vertical-align stabilește alinierea verticală (cum ar fi partea superioară, inferioară sau mijlocie) a conținutului în <th> sau <td>.
În mod implicit, alinierea verticală a conținutului dintr-un tabel este mijlocie (atât pentru elementele <th> cât și pentru <td>).
Table Padding
Pentru a controla spațiul dintre graniță și conținutul dintr-un tabel, utilizați proprietatea padding pentru elementele <td> și <th>.
Horizontal Dividers
Adăugați proprietatea border-bottom la <th> și <td> pentru horizontal dividers.
Hoverable Table
Utilizați selectorul :hover pe <tr> pentru a evidenția rândurile de tabel cu mouse over.
Striped Tables
Pentru tabele cu dungi zebră (zebra-striped tables), utilizați selecția nth-child() și adăugați o culoare de fundal la toate rândurile de tabele uniforme (sau impare).
Culoarea tabelului (Table Color)
Tabel responsiv (Responsive Table)
Un tabel responsiv va afișa o bară de defilare orizontală dacă ecranul este prea mic pentru a afișa întregul conținut.
Adăugați un element de container (cum ar fi <div>) cu overflow-x: auto în jurul elementului <table> pentru a face să răspundă.
În OS X Lion (pe Mac), barele de defilare sunt ascunse în mod implicit și sunt afișate doar atunci când sunt utilizate (chiar dacă „overflow: scroll” este setat).
Proprietățiile tabelului CSS:
border - Setează toate proprietățile de frontieră într-o singură declarație
border-collapse - Specifică dacă granițele tabelelor trebuie sau nu prăbușite
border-spacing - Specifică distanța dintre marginile celulelor adiacente
caption-side- Specifică amplasarea unei legi de tabel
empty-cells - Specifică dacă se afișează sau nu margini și fundal pe celulele goale dintr-un tabel
table-layout - Setează algoritmul de dispunere care va fi utilizat pentru o tabelă
CSS Display
Layout CSS - Proprietatea display
Proprietatea display este cea mai importantă proprietate CSS pentru controlul aspectului.
Proprietatea display
Proprietatea display specifică dacă / cum este afișat un element.
Fiecare element HTML are o valoare de afișare implicită în funcție de tipul de element. Valoarea implicită a afișajului pentru majoritatea elementelor este block sau inline.
Elemente la nivel de block (Block-level Elements)
Un element la nivel de block (block-level element) pornește întotdeauna pe o nouă linie și ocupă toată lățimea disponibilă (se întinde spre stânga și spre dreapta, cât poate).
Exemple de elemente la nivel de block (block-level element): <div>, <h1> - <h6>, <p>, <form>, <header>, <footer>, <section>.
Elemente în linie (Inline Elements)Un element inline nu pornește de pe o nouă linie și ocupă doar lățimea necesară.
Acesta este un element <span> inline din interiorul unui paragraf.
Exemple de elemente inlinie: <span>, <a>, <img>.
Display: none;
Display: none; este utilizat în mod obișnuit cu JavaScript pentru a ascunde și a arăta elementele fără a le șterge și recrea.
Elementul <script> folosește display: none; ca implicit.
Înlocuire Valoare implicită a afișajului
După cum am menționat, fiecare element are o valoare de afișare implicită. Cu toate acestea, puteți trece peste acest lucru.
Modificarea unui element inline într-un element de block, sau invers, poate fi utilă pentru ca pagina să arate într-un mod specific și să respecte în continuare standardele web.
Un exemplu obișnuit este crearea de elemente inline <li> pentru meniurile orizontale.
Setarea proprietății de afișare (display) a unui element modifică doar modul în care este afișat elementul, NU ce fel de element este. Deci, un element inline cu display: block; nu este permis să aibă alte elemente de block în interiorul său.
crearea de elemente inline <li> pentru meniurile orizontale.
afișare elemente <span> ca elemente de block.
afișare elemente <a> ca elemente de block.
Ascunde un element - display:none sau visibility:hidden?
Ascunderea unui element se poate face prin setarea proprietății dispaly la none. Elementul va fi ascuns, iar pagina va fi afișată ca și cum elementul nu este acolo.
visibility:hidden; ascunde de asemenea un element.
Cu toate acestea, elementul va ocupa totuși același spațiu ca înainte. Elementul va fi ascuns, dar afectează în continuare aspectul.
Proprietăți CSS de afișare / vizibilitate:
display - Specifică modul în care trebuie afișat un element.
visibility - Specifică dacă un element trebuie să fie vizibil sau nu.
CSS max-width
CSS Layout - width și max-width.
Utilizarea width, max-width și margin: auto;
Așa cum am menționat în capitolul precedent; un element la nivel de block (block-level element) ocupă întotdeauna întreaga lățime disponibilă (se întinde spre stânga și spre dreapta, cât poate).
Setarea lățimii (width) unui element la nivel de bloc (block-level element) va împiedica întinderea sa până la marginile containerului său. Apoi, puteți seta marginile la auto, pentru a centra orizontal elementul în containerul său. Elementul va prelua lățimea specificată, iar spațiul rămas va fi împărțit în mod egal între cele două margini.
Problema cu <div> de mai sus apare atunci când fereastra browserului este mai mică decât lățimea elementului. Browserul apoi adaugă o pagină de defilare orizontală la pagină.
Folosind în schimb această lățime maximă (max-width), în această situație, veți îmbunătăți gestionarea browserului de la ferestrele mici. Acest lucru este important atunci când faceți un site utilizabil pe dispozitive mici.
CSS Position
CSS Layout - Proprietatea position
Proprietatea position specifică tipul metodei de poziționare utilizate pentru un element (static, relativ, fix, absolut sau lipicios/static, relative, fixed, absolute sau sticky).
Elementele sunt apoi poziționate folosind proprietățiile de sus, de jos, de stânga și de dreapta (top, bottom, left, și right). Cu toate acestea, aceste proprietăți nu vor funcționa decât dacă proprietatea position este setată prima. De asemenea, funcționează diferit în funcție de valoarea poziției.
position: static; (poziție: static)
Elementele HTML sunt poziționate static în mod implicit.
Elementele poziționate static nu sunt afectate de proprietățile de sus, de jos, de stânga și de dreapta.
Un element cu position: static; (poziție: static) nu este poziționat într-un mod special; este poziționat întotdeauna în funcție de fluxul normal al paginii.
Element cu position: relative; (poziție: relativă;)
Un element cu position: relative; (poziție: relativă;) este poziționat în raport cu poziția normală.
Setarea proprietățiilor de sus, dreapta, jos și stânga a unui element relativ poziționat (relatively-positioned element) va face ca acesta să fie ajustat departe de poziția normală. Alt conținut nu va fi ajustat pentru a se încadra în niciun spațiu lăsat de element.
Elementul cu position: fixed; (poziție: fix;)
Un element cu position: fixed; (poziție: fix;) este poziționat în raport cu afișajul, ceea ce înseamnă că acesta rămâne întotdeauna în același loc, chiar dacă pagina este defilată. Proprietățile de sus, dreapta, jos și stânga sunt utilizate pentru poziționarea elementului.
Un element fix nu lasă un gol în pagina în care ar fi fost localizat în mod normal.
Elementul cu position: absolute; (poziție: absolută;)
Un element cu position: absolute; (poziție: absolută;) este poziționat în raport cu strămoșul cel mai apropiat poziționat (în loc de poziționat în raport cu vitrina, ca fix).
In orice caz; dacă un element poziționat absolut nu are strămoși poziționați, acesta folosește corpul documentului și se deplasează împreună cu derularea paginii.
Un element „poziționat” este unul a cărui poziție este orice, cu excepția staticii.
Elementul cu position: sticky; (poziție: lipicios;)
Un element cu position: sticky; (poziție: lipicios;) este poziționat în funcție de poziția de derulare a utilizatorului.
Un element lipicios (sticky) trece între relativ și fix, în funcție de poziția de defilare. Este poziționat relativ până când o poziție de offset dată este întâlnită în vitrină - apoi se „lipeste” în loc (ca poziția: fix).
Internet Explorer, Edge 15 și versiunile anterioare nu acceptă poziționarea sticky. Safari necesită un prefix -webkit- (vezi exemplul de mai jos). De asemenea, trebuie să specificați cel puțin una de sus, dreapta, jos sau stânga pentru ca poziționarea sticky să funcționeze.
În acest exemplu, elementul sticky se lipește în partea de sus a paginii (sus: 0), când atingeți poziția de defilare.
Elemente suprapuse (Overlapping Elements)
Când elementele sunt poziționate, se pot suprapune altor elemente.
Proprietatea indexului z specifică ordinea stivei unui element (care element trebuie plasat în fața sau în spatele celorlalte).
Un element poate avea o comandă a stivei pozitivă sau negativă.
Un element cu o ordine de stivă mai mare este întotdeauna în fața unui element cu o ordine de stivă mai mică.
Dacă două elemente poziționate se suprapun fără z - index specificat, elementul poziționat ultimul în codul HTML va fi afișat în partea de sus.
Poziționarea textului într-o imagine
Cum să poziționați textul peste o imagine.
Toate proprietățiile de poziționare CSS: bottom, clip, left, position, top, right, z-index.
bottom - Setează marginea inferioară a marginii pentru o casetă poziționată
clip - Clipsează un element absolut poziționat
left - Setează marginea din stânga pentru o cutie poziționată
position - Specifică tipul de poziționare pentru un element
right - Setează marginea din dreapta pentru o cutie poziționată
top - Setează marginea superioară a marginii pentru o casetă poziționată
z-index - Setează ordinea stivei unui element
CSS Overflow
Proprietatea CSS overflow controlează ce se întâmplă cu conținutul prea mare pentru a se încadra într-o zonă.
CSS Overflow
Proprietatea de overflow specifică dacă trebuie să decupați conținutul sau să adăugați bare de defilare atunci când conținutul unui element este prea mare pentru a se încadra în zona specificată.
Proprietatea de overflow are următoarele valori:
visible (vizibil) - implicit. Depășirea nu este tăiată. Conținutul este redat în afara casetei elementului.
hidden (ascuns) - preaplinul este tăiat, iar restul conținutului va fi invizibil.
scroll (defilare) - overflow-ul este tăiat și este adăugată o bară de defilare pentru a vedea restul conținutului.
auto - Similar cu defilarea, dar adaugă bare de defilare doar atunci când este necesar.
Elementul overflow: visible (revărsat: vizibil)
În mod implicit, revărsarea este vizibilă (overflow: visible), ceea ce înseamnă că nu este tăiată și se redă în afara casetei elementului.
Elementul overflow: hidden (revărsat: ascuns)
Odată cu valoarea ascunsă (overflow: hidden), preluarea este tăiată, iar restul conținutului este ascuns.
Elementul overflow: scroll (revărsat: defilare)
Setând valoarea pentru a derula (overflow: scroll), revărsarea este decupată și este adăugată o bară de defilare pentru a derula în interiorul casetei. Rețineți că aceasta va adăuga o bară de defilare atât pe orizontală cât și pe verticală (chiar dacă nu aveți nevoie de ea).
Elementele overflow-x și overflow-y
Proprietățiile de overflow-x și overflow specifică dacă trebuie să schimbe overflow-ul de conținut doar orizontal sau și vertical (sau ambele):
overflow-x specifică ce trebuie făcut cu marginile stânga / dreapta ale conținutului.
overflow-y specifică ce trebuie făcut cu marginile de sus / de jos ale conținutului.
Toate proprietățiile CSS de overflow:
overflow - Specifică ce se întâmplă dacă conținutul revărsă caseta unui element.
overflow-x - Specifică ce se poate face cu marginile stânga / dreapta ale conținutului dacă acesta revărsă zona de conținut a elementului.
overflow-y - Specifică ce trebuie făcut cu marginile de sus / de jos ale conținutului dacă acesta revărsă zona de conținut a elementului.
CSS Float
Proprietatea CSS float specifică modul în care un element ar trebui să plutească (float).
Proprietatea CSS clear specifică ce elemente pot pluti (float) lângă elementul șters și pe ce parte.
Proprietatea float
Proprietatea float este utilizată pentru poziționarea și formatarea conținutului, de ex. lăsați o imagine să plutească stânga spre text într-un container.
Proprietatea float poate avea una dintre următoarele valori:
left (stânga) - Elementul plutește în stânga containerului său.
right (dreapta) - Elementul plutește în dreapta containerului său.
none - Elementul nu plutește (va fi afișat acolo unde apare în text). Aceasta este implicită.
inherit (mostenire) - elementul moștenește valoarea float a părintelui său.
În cea mai simplă utilizare, proprietatea float poate fi utilizată pentru a înfășura text în jurul imaginilor.
Elementul float: right; (float: dreapta;).
Elementul float: left; (float: stânga;).
Elementul float: none;.
Proprietatea clear
Proprietatea clear specifică ce elemente pot pluti (float) lângă elementul șters și pe ce parte.
Proprietatea clear poate avea una dintre următoarele valori:
none - Permite elemente plutitoare de ambele părți. Aceasta este implicită.
left (stânga) - Nu sunt permise elemente plutitoare în partea stângă.
right (dreapta) - Nu sunt permise elemente plutitoare în partea dreaptă.
both (ambele) - Nu sunt permise elemente plutitoare nici pe partea stângă, fie pe partea dreaptă.
inherit (mostenirea) - Elementul mosteneste valoarea clara a parintelui său.
Cel mai obișnuit mod de a utiliza proprietatea clear este după ce ați utilizat o proprietate float pe un element.
Când ștergeți floats, ar trebui să potriviți clear cu float: Dacă un element este float la stânga, atunci ar trebui să ștergeți la stânga. Elementul float va continua să plutească, dar elementul șters va apărea sub el pe pagina web.
The clearfix Hack
Dacă un element este mai înalt decât elementul care îl conține și este float, acesta se va „overflow” în afara containerului său.
overflow: auto clearfix funcționează bine atâta timp cât sunteți în stare să păstrați controlul asupra margin-ului și a padding-ului (altfel puteți vedea bare de defilare). Totuși, noul clearfix hack however este mai sigur de utilizat și următorul cod este folosit pentru majoritatea paginilor web.
Grid of Boxes / Equal Width Boxes
Ce este box-sizing?
Puteți crea cu ușurință trei cutii plutitoare (floating boxes) una lângă alta. Cu toate acestea, când adăugați ceva care mărește lățimea fiecărei cutii (de exemplu, padding sau borders), caseta se va rupe. Proprietatea de dimensionare a cutiei ne permite să includem padding și border în lățimea totală (și înălțimea) a cutiei, asigurându-ne că padding rămâne în interiorul cutiei și că nu se rupe.
Grila casetelor poate fi de asemenea folosită pentru a afișa imagini side by side:
Cutii de înălțime egală (Equal Height Boxes)
Este bine dacă puteți garanta că casetele vor avea întotdeauna aceeași cantitate de conținut în ele. Dar de multe ori, conținutul nu este același. Dacă încercați exemplul de mai sus pe un telefon mobil, veți vedea că conținutul celei de-a doua cutii va fi afișat în afara casetei. Acesta este locul în care CSS3 Flexbox vine la îndemână - deoarece poate întinde automat cutiile pentru a fi la fel de lungă ca cea mai lungă casetă:
Flexbox nu este acceptat în Internet Explorer 10 sau în versiunile anterioare.
Meniu de navigatie (Navigation Menu)
Utilizați float cu o listă de hyperlinkuri pentru a crea un meniu orizontal.
Exemplu de dispunere web (Web Layout Example)
Este, de asemenea, obișnuit să faceți web layouts folosind proprietatea float.
Toate proprietățiile CSS float.
box-sizing Defineste modul în care se calculează lățimea și înălțimea unui element: trebuie să includă sau nu borduri
clear Specifica ce elemente pot pluti lângă elementul șters și pe ce parte
float Specifică modul în care un element trebuie să plutească
overflow Specifică ce se întâmplă dacă conținutul revărsă caseta unui element
overflow-x Specifică ce se poate face cu marginile stânga / dreapta ale conținutului dacă acesta revărsă zona de conținut a elementului
overflow-y Specifică ce trebuie făcut cu marginile de sus / de jos ale conținutului dacă acesta revărsă zona de conținut a elementului
CSS inline-block
The display: inline-block Value
În comparație cu display: inline, diferența majoră este aceea că display: inline-block permite să stabilească o lățime și o înălțime pe element.
De asemenea, cu display: inline-block, marginile de sus și de jos sunt respectate, dar cu display: inline nu sunt.
Față de display: block, diferența majoră este aceea că display: inline-block nu adaugă o pauză de linie după element, astfel încât elementul să poată sta lângă alte elemente.
Utilizarea inline-block pentru a crea legături de navigare.
O utilizare obișnuită pentru display: inline-block este de a afișa elemente de listă pe orizontală în loc de vertical.
CSS Align
CSS Layout - Aliniere orizontală și verticală
Elemente de aliniere de centru
Pentru a centra orizontal un element de block (cum ar fi <div>), utilizați margin: auto;
Setarea lățimii elementului îl va împiedica să se întindă până la marginile containerului său.
Elementul va prelua apoi lățimea specificată, iar spațiul rămas va fi împărțit în mod egal între cele două margini.
Notă: Alinierea la centru nu are efect dacă proprietatea lățimii nu este setată (sau setată la 100%).
Centrare aliniere text (Center Align Text)
Pentru a centra doar textul în interiorul unui element, utilizați text-align: center;
Centrați o imagine
Pentru a centra o imagine, setați marginea stângă și dreaptă pe auto și transformați-o într-un element block.
Aliniere stânga și dreapta - Folosire position
O metodă de aliniere a elementelor este utilizarea position: absolut ;:
Aliniere stânga și dreapta - Folosire float
O altă metodă pentru alinierea elementelor este utilizarea proprietății float.
Dacă un element este mai înalt decât elementul care îl conține și este float, acesta se va revărsa (overflow) în afara containerului său. Puteți utiliza hackul „clearfix” pentru a remedia acest lucru (a se vedea exemplul de mai jos).
The clearfix Hack
Putem adăuga overflow: auto; la elementul conținut pentru a remedia această problemă.
Centrare vertical - Folosire padding
Există multe moduri de a centra un element pe verticală în CSS. O soluție simplă este utilizarea paddingu-ului de sus și de jos.
Centru vertical - Folosire line-height
Un alt truc este să folosiți proprietatea line-height cu o valoare egală cu proprietatea height.
Centru vertical - Folosire position și transform
Dacă padding și line-height nu sunt opțiuni, o a treia soluție este utilizarea poziționării și a proprietății de transformare.
CSS Combinatoare
Un combinator este ceva care explică relația dintre selectori.
Un selector CSS poate conține mai mult de un simplu selector. Între selectoarele simple, putem include un combinator.
Există patru combinatoare diferite în CSS:
selector descendent (spațiu)
selector child (>)
selector sibling adiacent (+)
selector sibling general (~)
Selector descendent
Selectorul descendent se potrivește cu toate elementele care sunt descendenți ai unui element specificat.
Selectorul Child
Selectorul child selectează toate elementele care sunt copiii unui element specificat.
Selectorul sibling adiacent
Selectorul sibling adiacent selectează toate elementele care sunt frații adiacenți ai unui element specificat.
Elementele sibling trebuie să aibă același element părinte, iar „adiacent” înseamnă „urmărirea imediată”.
Selectorul sibling general
Selectorul sibling general selectează toate elementele care sunt frații unui element specificat.
Toți selectorii combinatori CSS.
element element div p - Selectează toate elementele <p> din interiorul elementelor <div>
element> element div> p - Selectează toate elementele <p> în care părintele este un element <div>
element + element div + p - Selectează toate elementele <p> care sunt plasate imediat după elementele <div>
element1 ~ element2 p ~ ul - Selectează fiecare element <ul> care este precedat de un element <p>
CSS Pseudo-clase
Ce sunt Pseudo-clasele?
O pseudo-clasă este utilizată pentru a defini o stare specială a unui element.
De exemplu, poate fi folosit pentru:
Stilează un element atunci când un utilizator trece cu mouseul peste el.
Stileaza linkurile vizitate și nevizitate diferit.
Stilează un element când se focusează.
Pseudo-clase ancorare
Linkurile pot fi afișate în diferite moduri.
a: hover TREBUIE să vină după a:link și a:visited în definiția CSS pentru a fi eficiente! a: active TREBUIE să vină după a:hover în definiția CSS pentru a fi eficient! Numele pseudo-class nu sunt case-sensitive.
Pseudo-clase și clase CSS
Pseudo-clasele pot fi combinate cu clase CSS.
Hover pe <div>
Simple Tooltip Hover
Hover peste un element <div> pentru a afișa un element <p> (cum ar fi un tooltip).
Pseudo-clasa CSS - :first-child
Pseudo-clasa :first-child se potrivește cu un element specificat care este primul copil al unui alt element.
Potriviți primul element <p>.
Potriviți primul element <i> din toate elementele <p>.
Potriviți toate elementele <i> din toate elementele primului copil <p>.
Pseudo-clasa CSS - :lang
Pseudo-clasa CSS - :lang vă permite să definiți reguli speciale pentru diferite limbi.
:lang definește ghilimele pentru elementele <q> cu lang = "no".
Toate clasele CSS Pseudo. Toate elementele CSS Pseudo.
CSS Pseudo-elemente
Un pseudo-element CSS este utilizat pentru a stabili părțile specificate ale unui element.
De exemplu, poate fi folosit pentru:
Stilizarea primei litere sau linia unui element.
Inserarea de conținut înainte sau după, conținutul unui element.
Observați notația dublă colon - :: first-line versus :first-line
Dublul colon a înlocuit notația cu un singur colon pentru pseudo-elemente în CSS3. Aceasta a fost o încercare din partea W3C de a distinge pseudo-clasele și pseudo-elementele.
Sintaxa cu un singur colon a fost folosită atât pentru pseudo-clase, cât și pentru pseudo-elemente în CSS2 și CSS1.
Pseudo-element :: first-line este utilizat pentru a adăuga un stil special la prima linie a unui text.
Pseudo-elementul :: first-line poate fi aplicat numai elementelor la nivel de block.
Următoarele proprietăți se aplică pentru pseudo-element :: first-line: font properties, color properties, background properties, word-spacing, letter-spacing, text-decoration, vertical-align, text-transform, line-height, clear
Pseudo-elementul :: first-letter este utilizat pentru a adăuga un stil special la prima literă a unui text.
Pseudo-elementul :: first-letter poate fi aplicat numai elementelor la nivel de block.
Următoarele proprietăți se aplică pentru pseudo-elementul :: first-letter: font properties, color properties , background properties, margin properties, padding properties, border properties, text-decoration, vertical-align (only if "float" is "none"), text-transform, line-height, float, clear
Pseudo-elemente și clase CSS
Pseudo-elementele pot fi combinate cu clase CSS.
Pseudo-elemente multiple
Mai multe pseudo-elemente pot fi, de asemenea, combinate.
Pseudo-elementul ::before poate fi utilizat pentru a insera un anumit conținut înainte de conținutul unui element.
Pseudo-elementul ::after poate fi utilizat pentru a insera un anumit conținut după conținutul unui element.
Pseudo-element ::selection se potrivește cu porțiunea unui element selectat de un utilizator.
Următoarele proprietăți CSS pot fi aplicate la ::selection: culoare, fundal, cursor și contur (color, background, cursor, și outline).
Toate Pseudo-elementele CSS:
::after p ::after - Inserați ceva după conținutul fiecărui element <p>
::before p ::before - Introduceți ceva înainte de conținutul fiecărui element <p>
::first letter p ::first letter - Selectează prima literă a fiecărui element <p>
::first-line p ::first-line - Selectează prima linie a fiecărui element <p>
::selection p ::selection - Selectează porțiunea unui element selectat de un utilizator
Toate Pseudo-clasele CSS:
:active a:active - Selectează legătura activă
:checked :input checked - Selectează fiecare element <input> bifat
:disabled :input disabled - Selectează fiecare element dezactivat <input>
:empty p:empty - Selectează fiecare element <p> care nu are copii
:enabled input:enabled - Selectează fiecare element activat <input>
:first-child p:first-child - Selectează toate elementele <p> care este primul copil al părintelui său
:first-of-type p:first-of-type - Selectează fiecare element <p> care este primul element <p> al părintelui său
:focus input:focus - Selectează elementul <input> care are focus
:hover a:hover - Selectează linkurile peste mouse
:in-range input:in-range - Selectează elementele <input> cu o valoare dintr-un interval specificat
:invalid :input invalid - Selectează toate elementele <input> cu o valoare nevalidă
:lang(language) p:lang(it) - Selectează fiecare element <p> cu o valoare a atributului lang începând cu „it”
:last-child p:last-child - Selectează toate elementele <p> care este ultimul copil al părintelui său
:last-of-type p:last-of-type - Selectează fiecare element <p> care este ultimul element <p> al părintelui său
:link a:link - Selectează toate linkurile nevizitate
:not (selector) :not (p) - Selectează fiecare element care nu este un element <p>
:nth-child (n) p:nth-child (2) - Selectează fiecare element <p> care este al doilea copil al părintelui său
:nth-last-child (n) p:nth-last-child (2) - Selectează fiecare element <p> care este al doilea copil al părintelui său, numărând de la ultimul copil
:nth-last-of-type (n) p:nth-last-of-type (2) - Selectează fiecare element <p> care este al doilea element <p> al părintelui său, numărând de la ultimul copil
:nth-of-type (n) p:nth-of-type (2) - Selectează fiecare element <p> care este al doilea element <p> al părintelui său
:only-of-type p:only-of-type - Selectează fiecare element <p> care este singurul element <p> al părintelui său
:only-child p:only-child - Selectează fiecare element <p> care este singurul copil al părintelui său
:optional input:optional - Selectează elementele <input> fără atribut "necesar"
:out-of-range input:out-of-range - Selectează elementele <input> cu o valoare în afara unui interval specificat
:read-only input:read-only - Selectează elementele <input> cu atributul „readonly” specificat
:read-write input:read-write - Selectează elementele <input> fără atribut "readonly"
:required input:required - Selectează elementele <input> cu atributul „necesar” specificat
:root root - Selectează elementul rădăcină al documentului
:target #news:target - Selectează elementul #news activ curent (faceți clic pe o adresă URL care conține numele ancorării)
:valid input:valid - Selectează toate elementele <input> cu o valoare valabilă
:visited a:visited - Selectează toate linkurile vizitate
CSS Opacitate / Transparență
Proprietatea opacity specifică opacitatea / transparența unui element.
Imagine transparentă
Proprietatea opacity poate lua o valoare între 0,0 și 1,0. Cu cât valoarea este mai mică, cu atât mai transparentă.
IE8 și utilizarea anterioară filter:alpha(opacity=x). X poate lua o valoare de la 0 la 100. O valoare mai mică face ca elementul să fie mai transparent.
Efectul Hover transparent
Proprietatea de opacitate este adesea folosită împreună cu: hover selector pentru a modifica opacitatea cu mouse-over.
Transparent Box
Când se utilizează proprietatea opacity pentru a adăuga transparență pe fundalul unui element, toate elementele sale copil moștenesc aceeași transparență. Acest lucru poate face textul într-un element complet transparent, greu de citit.
Transparență folosind RGBA
Dacă nu doriți să aplicați opacitate elementelor copil, folosiți valorile de culoare RGBA.
Ați aflat de la capitolul nostru de culori CSS, că puteți utiliza RGB ca valoare a culorii. În plus față de RGB, puteți utiliza o valoare a culorii RGB cu un canal alfa (RGBA) - care specifică opacitatea unei culori.
O valoare de culoare RGBA este specificată cu: rgba (roșu, verde, albastru, alfa). Parametrul alfa este un număr între 0,0 (complet transparent) și 1,0 (complet opac).
Text în Transparent Box.
CSS Bară de navigare
Bare de navigare
Navigarea ușor de utilizat este importantă pentru orice site web.
Cu CSS puteți transforma meniuri HTML plictisitoare în bare de navigare cu aspect bun.
Bară de navigare = Lista de legături
O bară de navigare are nevoie de HTML standard ca bază.
Bară de navigare dintr-o listă HTML standard.
O bară de navigare este practic o listă de legături, astfel încât utilizarea elementelor <ul> și <li> are sens perfect.
Link de navigare activ / curent
Adăugați o clasă „activă” la link-ul curent pentru a anunța utilizatorul pe ce pagină se află.
Link-uri centrate & adăugare borders
Adăugați text-align: center la <li> sau <a> pentru a centra legăturile.
Adăugați proprietatea border la <ul> Adăugați un border în jurul barei de navigare. Dacă doriți, de asemenea, borders în interiorul barei de navigare, adăugați un border-bottom la toate elementele <li>, cu excepția ultimului.
Full-height Fixed Vertical Navbar
Bară de navigare orizontală
Există două moduri de a crea o bară de navigare orizontală. Utilizarea elementelor din linie interioară sau flotantă.
Articole de listă inline
O modalitate de a construi o bară de navigare orizontală este de a specifica elementele <li> ca inline, pe lângă codul „standard” de mai sus.
display: inline; - În mod implicit, elementele <li> sunt elemente de tip block. Aici, eliminăm pauzele de linie înainte și după fiecare articol din listă, pentru a le afișa pe o singură linie.
Floating List Items
Un alt mod de a crea o bară de navigare orizontală este să float elementele <li> și să specifici un layout pentru link-urile de navigare.
Link de navigare activ / curent
Adăugați o clasă „active” la link-ul curent pentru a anunța utilizatorul pe ce pagină se află.
Link-uri aliniere dreapta (Right-align links)
Aliniați legăturile din dreapta, plutind elementele din listă spre dreapta (float: right;):
Border Dividers
Adăugați proprietatea border-right la <li> pentru a crea divizori de legături.
Fixed Navigation Bar
Faceți ca bara de navigare să rămână în partea de sus sau de jos a paginii, chiar și atunci când utilizatorul derulează pagina.
Fixed Top
Fixed Bottom
Bară orizontală gri
Sticky Navbar
Adăugați position: sticky; la <ul> pentru a crea sticky navbar.
Un element sticky trece între relativ și fix, în funcție de poziția de defilare. Este poziționat relativ până când o poziție dată de offset este întâlnită în viewport - apoi se „lipeste”la loc (ca position:fixed).
Internet Explorer, Edge 15 și versiunile anterioare nu acceptă poziționarea sticky. Safari necesită un prefix -webkit- (vezi exemplul de mai sus). De asemenea, trebuie să specificați cel puțin una de sus, dreapta, jos sau stânga pentru ca poziționarea sticky să funcționeze.
Responsive Topnav
Cum să utilizați interogări media CSS pentru a crea o navigare de sus.
Responsive Sidenav
Cum să utilizați interogări media CSS pentru a crea o navigare receptivă.
Dropdown Navbar
Cum să adăugați un meniu derulant într-o bară de navigare.
CSS Dropdowns
Basic Dropdown
Creați un dropdown box care apare când utilizatorul mută mouse-ul peste un element.
HTML) Utilizați orice element pentru a deschide conținutul dropdown, de ex. un element <span> sau un <button>.
Utilizați un element de container (cum ar fi <div>) pentru a crea conținut dropdown și adăugați orice doriți în interiorul acestuia.
Înfășurați un element <div> în jurul elementelor pentru a poziționa corect conținutul dropdown cu CSS.
CSS) Clasa .dropdown folosește position:relative, care este necesară atunci când dorim ca conținutul dropdown să fie plasat chiar sub butonul dropdown (folosind position:absolute).
Clasa .dropdown-content conține conținutul dropdown real. Este ascunsă în mod implicit și va fi afișată pe hover (vezi mai jos). Rețineți că min-width este setată la 160px. Simte-te liber să schimbi asta.
Dacă doriți ca lățimea conținutului dropdown să fie la fel de largă ca butonul dropdown, setați lățimea (width) la 100% (și overflow:auto pentru a activa defilarea pe ecrane mici).
În loc să folosim un border, am folosit proprietatea CSS box-shadow pentru a face ca meniul dropdown să arate ca un „card”.
Selectorul :hover este folosit pentru a afișa meniul dropdown atunci când utilizatorul mută mouse-ul peste butonul dropdown.
Dropdown Menu
Meniu dropdown care permite utilizatorului să aleagă o opțiune dintr-o listă.
Conținut dropdown aliniat la dreapta (Right-aligned Dropdown Content)
Dacă doriți ca meniul dropdown să meargă de la dreapta la stânga, în loc de la stânga la dreapta, adăugați right: 0;.
Imagine Dropdown
Cum să adăugați o imagine și alt conținut în dropdown box.
Dropdown Navbar
Cum să adăugați un meniu dropdown într-o bară de navigare.
CSS Galerie de imagini
CSS poate fi utilizat pentru a crea o galerie de imagini.
CSS Image Sprites
Image Sprites
Un image sprite este o colecție de imagini puse într-o singură imagine.
O pagină web cu multe imagini poate dura mult timp pentru a se încărca și generează mai multe solicitări de server.
Utilizarea image sprite-urilor va reduce numărul de solicitări de server și va economisi lățimea de bandă.
Cu CSS, putem afișa doar partea din imagine de care avem nevoie.
<img id = "home" src = "img_trans.gif"> - Definește doar o imagine transparentă mică, deoarece atributul src nu poate fi gol. Imaginea afișată va fi imaginea de fundal pe care o specificăm în CSS.
width: 46px; height: 44px; - Definește portiunea imaginii pe care dorim sa o folosim.
background: url(img_navsprites.gif) 0 0; - Definește imaginea de fundal și poziția acesteia (left 0px, top 0px).
Acesta este cel mai simplu mod de a utiliza image sprites, acum dorim să-l extindem folosind link-uri și efectele hover.
Image Sprites - Creați o listă de navigare
Imaginea sprite ("img_navsprites.gif") pentru a crea o listă de navigare.
Listă HTML, deoarece poate fi o legătură și acceptă și o imagine de fundal.
#navlist {position: relative;} - poziția este setată pe relativ pentru a permite poziționarea absolută în interiorul ei.
#navlist li {margin:0;padding:0;list-style:none;position:absolute;top:0;} - margin și padding sunt setate la 0, stilul listei este eliminat și toate elementele din listă sunt poziționate în mod absolut.
#navlist li, #navlist a {height:44px;display:block;} - înălțimea tuturor imaginilor este 44px.
Acum începe să poziționezi și stilul pentru fiecare parte specifică:
#home {left:0px;width:46px;} - poziționat până la stânga, iar lățimea imaginii este 46px.
#home {background:url(img_navsprites.gif) 0 0;} - definește imaginea de fundal și poziția acesteia (left 0px, top 0px)
#prev {left:63px;width:43px;} - poziționat 63px la dreapta (#home width 46px + puțin spațiu suplimentar între elemente), iar width este de 43px.
#prev {background:url('img_navsprites.gif') -47px 0;} - defineste imaginea de fundal 47px la dreapta (#home width 46px + 1px divisor de linie)
#next {left:129px;width:43px;} - poziționat 129px la dreapta (începutul #prev este 63px + #prev lățime 43px + spațiu suplimentar), iar lățimea este 43px.
#next {background:url('img_navsprites.gif') -91px 0;} - defineste imaginea de fundal 91px la dreapta (#home width 46px + 1px line diviser + #prev width 43px + 1px divisor line).
Image Sprites - Hover Effect
Adăugăm un efect hover în lista noastră de navigare.
Selectorul :hover poate fi utilizat pe toate elementele, nu numai pe linkuri.
("img_navsprites_hover.gif") conține trei imagini de navigare și trei imagini pe care să le utilizăm pentru efectele hover.
Deoarece este vorba de o singură imagine și nu de șase fișiere separate, nu va exista nicio întârziere de încărcare atunci când un utilizator trece peste imagine.
Adăugăm doar trei linii de cod pentru a adăuga efectul de hover.
#home a:hover {background: transparent url('img_navsprites_hover.gif') 0 -45px;} - Pentru toate cele trei imagini pasive, specificăm aceeași poziție de fundal, doar 45px mai jos.
CSS Selectori de atribute
Selectori de atribute CSS.
Elemente de stil HTML cu atribute specifice.
Este posibil să stilăm elemente HTML care au atribute specifice sau valori de atribut.
Selector CSS [atribute].
Selectorul [atribute] este utilizat pentru a selecta elemente cu un atribut specificat.
Selectarea tuturor elementelor <a> cu atributul target.
Selector CSS [attribute="value"]
Selectorul [attribute="value"] este utilizat pentru a selecta elemente cu un atribut și o valoare specificate.
Selectarea tuturor elementelor <a> cu atributul target = "_ blank".
Selector CSS [attribute~="value"]
Selectorul [attribute~="value"] este utilizat pentru a selecta elemente cu o valoare de atribut care conține un cuvânt specificat.
Selectarea tuturor elementelor cu un atribut title care conține o listă de cuvinte separată de spațiu, dintre care unul „flower”.
Selector CSS [attribute|="value"]
Selectorul [attribute|="value"] este utilizat pentru a selecta elementele cu atributul specificat începând cu valoarea specificată.
Selectarea tuturor elementelor cu o valoare de atribut class care începe cu "top".
Valoarea trebuie să fie un cuvânt întreg, fie singur, cum ar fi class = "top", sau urmat de o cratimă (-), cum ar fi class = "top-text"!
Selector CSS [attribute^="value"]
Selectorul [attribute^="value"] este utilizat pentru a selecta elemente a căror valoare de atribut începe cu o valoare specificată.
Selectarea tuturor elementelor cu o valoare de atribut class care începe cu "top".
Valoarea nu trebuie să fie un cuvânt întreg!
Selector CSS [attribute$="value"]
Selectorul [attribute$="value"] este utilizat pentru a selecta elementele a căror valoare de atribut se termină cu o valoare specificată.
Selectarea tuturor elementelor cu valoarea de atribut class care se încheie cu "test".
Valoarea nu trebuie să fie un cuvânt întreg!
Selector CSS [attribute*="value"]
Selectorul [attribute*="value"] este utilizat pentru a selecta elementele a căror valoare de atribut conține o valoare specificată.
Selectarea tuturor elementelor cu valoarea de atribut class care conține "te".
Valoarea nu trebuie să fie un cuvânt întreg!
Styling Forms
Selectoarele de atribute pot fi utile pentru stilul formularelor fără clasă sau ID.
Toți selectorii de atribute CSS
[attribute] [target] - Selectează toate elementele cu un atribut țintă (target)
[attribute=value] [target=_blank] - Selectează toate elementele cu target = "_ blank"
[attribute~=value] [title~=flower] - Selectează toate elementele cu un atribut titlu care conține cuvântul "flower"
[attribute|=value] [lang|=en] - Selectează toate elementele cu o valoare a atributului lang care începe cu "en"
[attribute^=value] a[href^="https"] - Selectează fiecare element <a> a cărui valoare a atributului href începe cu "https"
[attribute$=value] a[href$=".pdf"] - Selectează fiecare element <a> a cărui valoare a atributului href se încheie cu ".pdf"
[attribute*=value] a[href*="w3schools"] - Selectează fiecare element <a> a cărui valoare a atributului href conține substratul "w3schools"
CSS Formulare
Formulare CSS
Aspectul unui formular HTML poate fi îmbunătățit mult cu CSS.
Stilizarea câmpurilor de intrare (Styling Input Fields)
Utilizați proprietatea width pentru a determina lățimea câmpului de intrare (input field).
Dacă doriți să stilați un tip de intrare specific, puteți utiliza selectori de atribute:
input [type=text] - va selecta doar câmpurile de tip text
input [type=password] - va selecta doar câmpuri de tip parolă
input [type=number] - va selecta doar câmpuri numerice
Padded Inputs
Utilizați proprietatea padding pentru a adăuga spațiu în câmpul text.
Când aveți multe intrări una după cealaltă, este posibil să doriți să adăugați și o anumită marjă (margin), pentru a adăuga mai mult spațiu în afara lor.
Bordered Inputs
Utilizați proprietatea border pentru a modifica dimensiunea și culoarea border-ului și utilizați proprietatea border-radius pentru a adăuga colțuri rotunjite(corners rounded).
Dacă doriți doar un bottom border, utilizați proprietatea border-bottom.
Colored Inputs
Utilizați proprietatea background-color pentru a adăuga o culoare de fundal la intrare și proprietatea color pentru a schimba culoarea textului.
Focused Inputs
În mod implicit, unele browsere vor adăuga un contur (outline) albastru în jurul intrării atunci când va fi focalizat (faceți click pe). Puteți elimina acest comportament adăugând outline: none; la intrare.
Utilizați selectorul :focus pentru a face ceva cu câmpul de introducere atunci când este focalizat.
Intrare cu pictogramă / imagine(Input with icon/image)
Dacă doriți o pictogramă (icon) în interiorul intrării, utilizați proprietatea background-image și poziționați-o cu proprietatea background-position. Rețineți, de asemenea, că adăugăm un left padding mare pentru a rezerva spațiul pictogramei (icon).
Intrare de căutare animată(Animated Search Input)
În acest exemplu, utilizăm proprietatea CSS transition pentru a anima lățimea (width) intrării de căutare atunci când devine focus.
Styling Textareas
Utilizați proprietatea resize pentru a împiedica redimensionarea textului (dezactivați „grabber” din colțul din dreapta jos):
Styling Select Menus
Stilizarea butoanelor de intrare(Styling Input Buttons)
Formular responsiv(Responsive Form)
Redimensionați fereastra browserului pentru a vedea efectul. Când ecranul are o lățime mai mică de 600px, faceți ca cele două coloane să se stivească una peste alta, în loc de una lângă alta.
Interogări media pentru a crea un formular cu răspuns.
CSS Contoare
Contoare CSS
Contoarele CSS sunt „variabile” menținute de CSS ale căror valori pot fi incrementate prin reguli CSS (pentru a urmări de câte ori sunt utilizate). Contoarele vă permit să ajustați aspectul conținutului în funcție de plasarea acestuia în document.
Numerotare automată cu contoare
Contoarele CSS sunt ca „variabile”. Valorile variabilei pot fi incrementate prin reguli CSS (care vor urmări de câte ori sunt utilizate).
Pentru a lucra cu contoarele CSS vom folosi următoarele proprietăți:
counter-reset - Creează sau resetează un contor
counter-increment - Crește o valoare a contorului
content - Inserează conținut generat
counter() or counters() function - Adăugă valoarea unui contor la un element
Pentru a utiliza un contor CSS, acesta trebuie mai întâi creat cu counter-reset.
Creează un contor pentru pagină (în selectorul body), apoi crește valoarea contorului pentru fiecare element <h2> și adaugă "Secțiunea <valoarea contorului>:" la începutul fiecărui element <h2>.
Nesting Counters
Creează un contor pentru pagină (section) și un contor pentru fiecare element <h1> (subsection). Contorul „section” va fi contorizat pentru fiecare element <h1> cu „secțiunea <valoarea secțiunii contorului>.”, Iar contorul „subsection” va fi contorizat pentru fiecare element <h2> cu „<valoarea contorului de secțiuni >. <valoarea contorului de subsecțiuni> ".
Un contor poate fi de asemenea util pentru a crea liste conturate, deoarece o nouă instanță a unui contor este creată automat în elementele copil. Folosim funcția counters() pentru a insera o șir între diferitele niveluri de nested counters.
content - Folosit cu pseudo-elementele ::before și ::after, pentru a insera conținut generat
counter-increment - Crește una sau mai multe valori ale contorului
counter-reset - Creează sau resetează unul sau mai multe contoare
CSS Website Layout
Website Layout
Un site web este adesea împărțit în anteturi, meniuri, conținut și un subsol(headers, menus, content și footer).
Antet (Header)
Un antet este de obicei situat în partea de sus a site-ului web (sau chiar sub un meniu de navigare de sus). Adesea conține un logo sau numele site-ului.
Bară de navigare (Navigation Bar)
O bară de navigare conține o listă de link-uri pentru a ajuta vizitatorii care navighează pe site-ul dvs. web.
Conţinut (Content)
Aspectul din această secțiune depinde adesea de utilizatorii vizați. Cea mai comună dispunere este una (sau combinarea lor) dintre următoarele:
1-column - (adesea folosit pentru browserele mobile)
2-column - (adesea folosit pentru tablete și laptopuri)
3-column layout - (utilizată doar pentru desktopuri)
Coloane inegale (Unequal Columns)
Conținutul principal este cea mai mare și cea mai importantă parte a site-ului dvs.
Este comună cu lățimile inegale ale coloanei, astfel încât cea mai mare parte a spațiului este rezervată conținutului principal. Conținutul lateral (dacă există) este adesea folosit ca o navigare alternativă sau pentru a specifica informații relevante pentru conținutul principal. Modificați lățimile după cum doriți, amintiți-vă doar că ar trebui să adauge până la 100% în total.
Subsol (Footer)
Subsolul este plasat în partea de jos a paginii. Adesea conține informații precum copyright și informații de contact.
Responsive Website Layout
Folosind o parte din codul CSS de mai sus, putem crea un site web responsiv, care variază între două coloane și coloane cu lățime completă, în funcție de lățimea ecranului.
CSS Unități
Unități CSS
CSS are mai multe unități diferite pentru exprimarea unei lungimi.
Multe proprietăți CSS iau valori „de lungime” (lenght), cum ar fi lățimea, marja, căptușirea, dimensiunea fontului etc (width, margin, padding, font-size).
Lungimea este un număr urmat de o unitate de lungime, cum ar fi 10px, 2em etc.
Un whitespace nu poate apărea între număr și unitate. Cu toate acestea, dacă valoarea este 0, unitatea poate fi omisă.
Pentru unele proprietăți CSS, lungimile negative sunt permise.
Există două tipuri de unități de lungime: absolută și relativă.
Lungimi absolute (Absolute Lengths)
Unitățile de lungime absolută sunt fixe și o lungime exprimată în oricare dintre acestea va apărea exact ca acea dimensiune.
Unitățile de lungime absolută nu sunt recomandate pentru utilizare pe ecran, deoarece dimensiunile ecranului diferă atât de mult. Cu toate acestea, pot fi utilizate dacă este cunoscut suportul de ieșire, cum ar fi pentru aspectul tipăririi.
cm - centimetri
mm - millimetri
in - inci (1in = 96px = 2.54cm)
px * - pixeli (1px = 1/96th of 1in)
pt - puncte (1pt = 1/72 of 1in)
pc - picas (1pc = 12 pt)
* Pixelii (px) sunt în raport cu dispozitivul de vizualizare. Pentru dispozitivele cu valoare redusă, 1px este un pixel de dispozitiv (punct) al afișajului. Pentru imprimante și ecrane de înaltă rezoluție, 1px implică mai mulți pixeli de dispozitiv.
Lungimi relative (Relative Lengths)
Unitățile de lungime relativă specifică o lungime relativă la o altă proprietate lungime. Unitățile de lungime relativă scalează mai bine între diferite medii de redare.
em - În raport cu dimensiunea fontului elementului (2em înseamnă de 2 ori dimensiunea fontului curent)
ex - În raport cu înălțimea x a fontului curent (rar folosit)
ch - În raport cu lățimea "0" (zero)
rem - Relativ la dimensiunea fontului elementului rădăcină
vw - În raport cu 1% din lățimea afișajului *
vh - În raport cu 1% din înălțimea viewport *
vmin - În raport cu 1% din dimensiunea mai mică a portofoliului *
vmax - În raport cu 1% din dimensiunea mai mare a portofoliului
% - În raport cu elementul părinte
Unitățile em și rem sunt practice în crearea unui aspect scalabil perfect!
* Viewport = dimensiunea ferestrei browserului. Dacă viewport are 50cm lățime, 1vw = 0,5cm.
Asistență browser (Browser Support)
Numerele din tabel specifică prima versiune a browserului care acceptă integral unitatea de lungime.
CSS Specificitate
Specificitatea CSS
Dacă există două sau mai multe reguli CSS conflictuale care indică același element, browserul respectă câteva reguli pentru a determina care este cea mai specifică și, prin urmare, câștigă.
Gândiți-vă la specificitate ca punctaj / rang care determină ce declarații de stil sunt aplicate unui element în cele din urmă.
Selectorul universal (*) are specificitate scăzută, în timp ce selectoarele ID sunt foarte specifice!
Specificitatea este un motiv comun pentru care regulile CSS nu se aplică anumitor elemente, deși credeți că ar trebui.
Ierarhia specificității (Specificity Hierarchy)
Fiecare selector își are locul în ierarhia specificității. Există patru categorii care definesc nivelul de specificitate al unui selector:
Stiluri în linie (Inline styles) - Un stil inline este atașat direct la elementul care urmează să fie stilat. Exemplu: <h1 style = "color: #ffffff;">.
ID-uri (IDs) - Un ID este un identificator unic pentru elementele paginii, cum ar fi #navbar.
Clase, atribute și pseudo-clase - Această categorie include .classes, [attributes] and pseudo-classes, cum ar fi :hover, :focus etc.
Elemente și pseudo-elemente - Această categorie include nume de elemente și pseudo-elemente, cum ar fi h1, div, :before și :after.
Cum se calculează specificitatea?
Memorează cum să calculezi specificitatea!
Începeți de la 0, adăugați 1000 pentru atributul style, adăugați 100 pentru fiecare ID, adăugați 10 pentru fiecare atribut, clasă sau pseudo-clasă, adăugați 1 pentru fiecare nume de element sau pseudo-element.
Specificitatea lui A este 1 (un element)
Specificitatea lui B este 101 (o referință ID și un element)
Specificitatea C este 1000 (stil în linie)
De la 1 <101 <1000, a treia regulă (C) are un nivel mai mare de specificitate și, prin urmare, va fi aplicată.
Reguli de specificitate (Specificity Rules)
Specificitate egală: ultima regulă contează - Dacă aceeași regulă este scrisă de două ori în foaia de stil externă (external style sheet), atunci regula inferioară din foaia de stil (style sheet) este mai aproape de elementul care trebuie stilizat și, prin urmare, va fi aplicată.
Ultima regulă este întotdeauna aplicată.
Selectoarele ID au o specificitate mai mare decât selectoarele de atribute.
Prima regulă este mai specifică decât celelalte două și va fi aplicată.
Selectoarele contextuale sunt mai specifice decât un singur selector de elemente - Foaia de stil încorporată este mai aproape de elementul care urmează să fie stilat.
Ultima normă va fi aplicată.
Un selector de clasă bate orice număr de selectori de elemente - un selector de clase, cum ar fi .intro beats h1, p, div, etc.
Selectorul universal și valorile moștenite au o specificitate de 0 - *, body * și similare au o specificitate zero. Valorile moștenite au, de asemenea, o specificitate de 0.
CSS Colțuri rotunjite
CSS Colțuri rotunjite
Cu proprietatea CSS border-radius, puteți da oricărui element "colțuri rotunjite" (rounded corners).
Proprietate CSS border-radius
Proprietatea CSS border-radius definește raza colțurilor unui element.
Această proprietate vă permite să adăugați colțuri rotunjite la elemente!
Colțuri rotunjite (rounded corners) pentru un element cu o culoare de fundal specificată.
Colțuri rotunjite (rounded corners) pentru un element cu bordură.
Colțuri rotunjite (rounded corners) pentru un element cu o imagine de fundal.
Proprietatea „border-radius” este de fapt o proprietate de tip shorthand pentru proprietățiile border-top-left-radius, border-top-right-radius, border-bottom-right-radius și border-bottom-left-radius.
CSS border-radius - Specificați fiecare colț
Proprietatea border-radius poate avea de la una până la patru valori.
Patru valori - border-radius: 15px 50px 30px 5px; (prima valoare se aplică colțului din stânga sus(top-left corner), a doua valoare se aplică colțului din dreapta sus(top-right corner), a treia valoare se aplică colțului din dreapta jos(bottom-right corner) și a patra valoare se aplică colțului din stânga jos(bottom-left corner)).
Trei valori - border-radius: 15px 50px 30px; (prima valoare se aplică colțului din stânga sus(top-left corner), a doua valoare se aplică colțurilor din dreapta sus și din stânga jos(top-right și bottom-left corners) și a treia valoare se aplică colțului din dreapta jos(bottom-right corner)).
Două valori - border-radius: 15px 50px; (prima valoare se aplică colțurilor din stânga sus și din dreapta jos(top-left și bottom-right corners), iar a doua valoare se aplică colțurilor din dreapta sus și din stânga jos(top-right și bottom-left corners)).
O valoare - border-radius: 15px; (valoarea se aplică la toate cele patru colțuri, care sunt rotunjite în mod egal).
Proprietăți CSS Rounded Corners
border-radius O proprietate shorthand pentru setarea tuturor celor patru chenare - * - * - proprietăți radius.
border-top-left-radius Definește forma marginii din colțul din stânga sus.
border-top-right-radius Definește forma marginii din colțul din dreapta sus.
border-bottom-right-radius Definește forma marginii din colțul din dreapta jos.
border-bottom-left-radius Definește forma marginii din colțul din stânga jos.
CSS Border Images
CSS Border Images
Cu proprietatea CSS border-image, puteți seta o imagine care să fie utilizată ca border în jurul unui element.
Proprietatea CSS border-image
Proprietatea CSS border-image vă permite să specificați o imagine care trebuie utilizată în loc de bordura normală din jurul unui element.
Proprietatea are trei părți:
Imaginea utilizată ca border.
Unde să tăiați imaginea.
Definiți dacă secțiunile din mijloc trebuie repetate sau întinse.
Proprietatea border-image ia imaginea și o taie în nouă secțiuni, precum o placă tic-tac-toe. Apoi plasează colțurile la colțuri, iar secțiunile din mijloc sunt repetate sau întinse după cum specificați.
Pentru ca border-image să funcționeze, elementul are nevoie și de setul de proprietăți border!
Secțiunile din mijloc ale imaginii sunt repetate pentru a crea border.
Secțiunile din mijloc ale imaginii sunt întinse pentru a crea border.
Proprietatea border-image este de fapt o proprietate de tip shorthand pentru proprietățile border-image-source, border-image-slice, border-image-width, border-image-outset și border-image-repeat.
CSS border-image - Different Slice Values
Different slice values schimbă complet aspectul border-ului.
Proprietățiile CSS Border Image
border-image - O proprietate shorthand pentru setarea tuturor proprietăților border-image- *.
border-image-source - Specifică calea către imaginea care va fi utilizată ca border.
border-image-slice - Specifică modul de tăiere a border image.
border-image-width - Specifică lățimile pentru border image.
border-image-outset - Specifică cantitatea prin care se extinde zona border image dincolo de border box.
border-image-repeat - Specifică dacă border image trebuie repetată, rotunjită sau întinsă.
CSS Fundaluri multiple
În acest capitol veți învăța cum să adăugați mai multe imagini de fundal la un element.
Proprietățiile background-size, background-origin, background-clip.
CSS vă permite să adăugați mai multe imagini de fundal pentru un element, prin proprietatea background-image.
Diferitele imagini de fundal sunt separate prin virgule, iar imaginile sunt stivuite una peste alta, unde prima imagine este cea mai apropiată de privitor.
Mai multe imagini de fundal pot fi specificate utilizând fie proprietățiile de fundal individuale (ca mai sus), fie proprietatea background shorthand.
CSS Background Size
Proprietatea CSS background-size vă permite să specificați dimensiunea imaginilor de fundal.
Mărimea poate fi specificată în lungimi, procente (lengths, percentages) sau utilizând unul dintre cele două cuvinte cheie: conține sau acoperire(contain sau cover).
Redimensionare background image la o dimensiune mult mai mică decât imaginea originală (folosind pixeli).
Celelalte două valori posibile pentru background-size sunt contain și cover.
Cuvântul cheie contain scalează imaginea de fundal (scales the background image) pentru a fi cât mai mare (dar atât lățimea cât și înălțimea sa trebuie să se încadreze în zona conținutului). Ca atare, în funcție de proporțiile imaginii de fundal (background image) și de zona de poziționare a fundalului, pot exista anumite zone ale fundalului care nu sunt acoperite de imaginea de fundal (background image).
Cuvântul cheie cover scalează imaginea de fundal (scales the background image) astfel încât zona de conținut să fie acoperită complet de imaginea de fundal (background image) (atât lățimea cât și înălțimea acesteia sunt egale sau depășesc aria conținutului). Ca atare, este posibil ca unele părți ale imaginii de fundal (background image) să nu fie vizibile în zona de poziționare a fundalului.
Definirea dimensiunilor mai multor imagini de fundal (Define Sizes of Multiple Background Images)
Proprietatea background-size acceptă, de asemenea, mai multe valori pentru dimensiunea fundalului (folosind o listă separată de virgule), atunci când lucrați cu mai multe fundaluri.
Full Size Background Image
Acum vrem să avem o imagine de fundal (background image) pe un site web care să acopere întreaga fereastră a browserului în orice moment.
Cerințele sunt următoarele:
Completează întreaga pagină cu imaginea (fără spațiu alb).
Scalați imaginea după caz.
Centrați imaginea pe pagina.
Nu provocați bare de defilare (scrollbars).
Hero Image
De asemenea, puteți utiliza diferite proprietăți de fundal (background) pe un <div> pentru a crea hero image (o imagine mare cu text) și să o plasați acolo unde doriți.
Proprietatea CSS background-origin
Proprietatea CSS background-origin specifică unde este poziționată imaginea de fundal.
Proprietatea are trei valori diferite:
border-box - imaginea de fundal pornește din colțul din stânga sus al border-ului.
padding-box - (implicit) imaginea de fundal pornește din colțul din stânga sus al marginii padding-ului.
content-box - imaginea de fundal pornește din colțul din stânga sus al conținutului.
Proprietatea CSS background-clip
Proprietatea CSS background-clip specifică zona de pictură a fundalului.
Proprietatea are trei valori diferite:
border-box - (implicit) fundalul este pictat pe marginea exterioară a border-ului.
padding-box - fundalul este vopsit până la marginea exterioară a padding-ului.
content-box - fundalul este pictat în caseta de conținut.
Proprietăți CSS background avansate:
background - O proprietate shorthand pentru setarea tuturor proprietăților de fundal într-o singură declarație
background-clip - Specifică zona de pictură a fundalului
background-image - Specifică una sau mai multe imagini de fundal pentru un element
background-origin - Specifică unde este / sunt poziționate imaginile de fundal
background-size - Specifică dimensiunea imaginii de fundal
CSS Culori
Culori CSS
CSS acceptă 140+ nume de culoare, valori HEX, valori RGB, valori RGBA, valori HSL, valori HSLA și opacitate.
Culori RGBA
Valorile de culoare RGBA sunt o extensie a valorilor de culoare RGB cu un canal alfa - care specifică opacitatea unei culori.
O valoare de culoare RGBA este specificată cu: rgba (roșu, verde, albastru, alfa)/rgba(red, green, blue, alpha). Parametrul alfa este un număr între 0,0 (complet transparent) și 1,0 (complet opac).
HSL Colors
HSL înseamnă Hue, Saturation and Lightness.
O valoare de culoare HSL este specificată cu: hsl(hue, saturation, lightness).
Hue este un grad pe roata de culoare (de la 0 la 360):
0 (sau 360) este roșu
120 este verde
240 este albastru
Saturation este o valoare procentuală: 100% este culoarea completă.
Lightness este, de asemenea, un procent; 0% este întunecat (negru) și 100% alb.
Culorile HSLA
Valorile de culoare HSLA sunt o extensie a valorilor de culoare HSL cu un canal alfa - care specifică opacitatea unei culori.
O valoare de culoare HSLA este specificată cu: hsla(hue, saturation, lightness, alpha), unde parametrul alfa definește opacitatea. Parametrul alfa este un număr între 0,0 (complet transparent) și 1,0 (complet opac).
Opacitate
Proprietatea CSS opacity stabilește opacitatea pentru întregul element (atât culoarea de fundal, cât și textul vor fi opace / transparente).
Valoarea proprietății de opacitate trebuie să fie un număr între 0,0 (complet transparent) și 1,0 (complet opac).
CSS Gradienți
Gradienți CSS
Gradienții CSS vă permit să afișați tranziții netede între două sau mai multe culori specificate.
CSS definește două tipuri de gradienți:
Gradienți liniari/Linear Gradients (coboară / în sus / stânga / dreapta / în diagonală)
Gradienți radiali/Radial Gradients (definiți de centrul lor)
Gradienți liniari CSS
Pentru a crea un gradient liniar trebuie să definiți cel puțin două opriri de culoare (color stops). Oprirea culorilor (color stops) se referă la culorile dintre care doriți să faceți tranziții netede. Puteți seta, de asemenea, un punct de plecare și o direcție (sau un unghi) împreună cu efectul de gradient.
Gradient liniar - de sus în jos (aceasta este implicit)
Gradient liniar care începe de sus. Începe roșu, iar trecerea se face la galben
Gradient liniar - de la stânga la dreapta (Linear Gradient - Left to Right)
Gradient liniar care pornește de la stânga. Începe roșu, trecerea se face la galben.
Gradient liniar - diagonală (Linear Gradient - Diagonal)
Puteți face un gradient în diagonală specificând atât pozițiile de pornire orizontale, cât și cele verticale.
Gradient liniar care începe în stânga sus (și merge spre dreapta jos). Începe roșu, trecerea se face la galben.
Utilizarea unghiurilor (Using Angles)
Dacă doriți un control mai mare asupra direcției gradientului, puteți defini un unghi, în loc de direcțiile predefinite (în jos, în sus, în dreapta, în stânga, în dreapta jos etc.).
Unghiul este specificat ca un unghi între o linie orizontală și linia de gradient.
Modul de utilizare a unghiurilor pe gradienți liniari.
Folosirea mai multor opriri de culori (Using Multiple Color Stops)
Un gradient liniar (de sus în jos) cu mai multe opriri de culoare(multiple color stops).
Un gradient liniar (de la stânga la dreapta) cu culoarea curcubeului și cu un text.
Utilizarea transparenței (Using Transparency)
De asemenea, gradienții CSS acceptă transparența, care poate fi utilizată pentru a crea efecte de decolorare.
Pentru a adăuga transparență, folosim funcția rgba() pentru a defini oprirea culorii (color stops). Ultimul parametru din funcția rgba () poate fi o valoare de la 0 la 1 și definește transparența culorii: 0 indică transparență completă, 1 indică culoarea completă (fără transparență).
Un gradient liniar care pornește de la stânga. Începe complet transparent, trecând la roșu complet.
Repetarea unui gradient liniar (Repeating a linear-gradient)
Funcția repeating-linear-gradient() este utilizată pentru a repeta gradienți liniari:
Gradienți radiali CSS (CSS Radial Gradients)
Un gradient radial este definit de centrul său.
Pentru a crea un gradient radial trebuie să definiți, de asemenea, cel puțin două opriri de culoare (color stops).
În mod implicit, forma este de elipsă, dimensiunea este cea mai îndepărtată de colț, iar poziția este centrală.
Gradient radial - Opriri uniforme ale culorilor/ Radial Gradient - Evenly Spaced Color Stops (aceasta este implicită)
Un gradient radial cu opriri uniforme de culoare distanțate.
Gradient radial - Opriri de culori distanțate diferit / Radial Gradient - Differently Spaced Color Stops
Un gradient radial cu opriri de culoare distanțate diferit.
Setați forma (Set Shape)
Parametrul shape definește forma. Poate lua cercul de valori sau elipsa. Valoarea implicită este elipsa.
Un gradient radial sub forma unui cerc.
Utilizarea cuvintelor cheie de dimensiuni diferite (Use of Different Size Keywords)
Parametrul size definește dimensiunea gradientului. Poate lua patru valori: closest-side, farthest-side, closest-corner, farthest-corner.
Un gradient radial cu cuvinte cheie de dimensiuni diferite.
Repetarea unui gradient radial (Repeating a radial-gradient)
Funcția repeating-radial-gradient() este utilizată pentru a repeta gradienți radiali.
Proprietăți CSS pentru gradient
background-image - Setează una sau mai multe imagini de fundal pentru un element.
CSS Efecte de umbră
Efecte de umbră CSS
Cu CSS puteți adăuga umbră textului și elementelor.
Proprietăți: text-shadow, box-shadow.
Umbre multiple (Multiple Shadows)
Pentru a adăuga mai mult de o umbră textului, puteți adăuga o listă de umbre separate de virgule.
Umbră de strălucire neon roșu și albastru.
Text alb cu umbra neagră, albastră și albastru închis
Puteți utiliza, de asemenea, proprietatea text-shadow pentru a crea un chenar simplu în jurul unui text (fără umbre)
Proprietatea CSS box-shadow
Proprietatea CSS box-shadow aplică umbre pentru elemente.
În cea mai simplă utilizare, specificați doar umbra orizontală și umbra verticală.
Apoi, adăugați o culoare la umbră.
Apoi, adăugați un efect de estompare la umbră.
Puteți adăuga, de asemenea, umbre la pseudo-elemente ::before și ::after pentru a crea un efect interesant.
Cards
Un exemplu de utilizare a proprietății box-shadow pentru a crea paper-like cards.
Proprietăți CSS Shadow
box-shadow - Adaugă una sau mai multe umbre la un element.
text-shadow - Adăugă una sau mai multe umbre la un text.
CSS Efecte de text
CSS Text Overflow, Word Wrap, Line Breaking Rules și Writing Modes
Proprietăți: text-overflow, word-wrap, word-break, writing-mode
CSS Text Overflow
Proprietatea CSS text-overflow specifică modul în care conținutul overflowed care nu este afișat trebuie semnalat utilizatorului.
Poate fi decupat sau poate fi redat ca elipsă (...).
CSS Word Wrapping
Proprietatea CSS word-wrap permite cuvintelor lungi să poată fi broken și wrap pe linia următoare.
Dacă un cuvânt este prea lung pentru a se încadra într-o zonă, acesta se extinde în afara.
Proprietatea word-wrap vă permite să forțați textul să fie wrap - chiar dacă înseamnă împărțirea în mijlocul unui cuvânt.
CSS Word Breaking
Proprietatea CSS word-break specifică regulile de rupere a liniei.
Mod de scriere CSS (CSS Writing Mode)
Proprietatea CSS writing-mode specifică dacă liniile de text sunt dispuse orizontal sau vertical.
Proprietăți CSS Text Effect:
text-align-last - Specifică modul de aliniere la ultima linie a unui text
text-justify - Specifică modul în care textul justify ar trebui să fie aliniat și distanțat
text-overflow - Specifică modul în care conținutul revărsat care nu este afișat trebuie semnalat utilizatorului
word-break - Specifică regulile de rupere de linie pentru scripturile care nu sunt CJK
word-wrap - Permite cuvintele lungi pentru a putea fi broken și wrap pe linia următoare
writing-mode - Specifică dacă liniile de text sunt dispuse orizontal sau vertical
CSS Fonturi Web
Fonturi Web CSS
Regula CSS @ font-face
Fonturile web permit proiectanților web să utilizeze fonturi care nu sunt instalate pe computerul utilizatorului.
Când a-ți găsit / cumpărat fontul pe care doriți să-l utilizați, includeți doar fișierul font pe serverul dvs. web, iar acesta va fi descărcat automat la nevoie.
Fonturile dvs. proprii sunt definite în regula CSS @font-face.
Diferite formate de fonturi (Different Font Formats)
Fonturi TrueType (TTF)
TrueType este un standard de font dezvoltat la sfârșitul anilor 1980, de Apple și Microsoft. TrueType este cel mai frecvent format de font atât pentru sistemele de operare Mac OS cât și pentru Microsoft Windows.
Fonturi OpenType (OTF)
OpenType este un format pentru fonturile computerului scalabile. A fost construit pe TrueType și este marcă înregistrată a Microsoft. Fonturile OpenType sunt utilizate astăzi frecvent pe majore platforme de calculatoare.
Web Open Font Format (WOFF)
WOFF este un format de font folosit pentru paginile web. A fost dezvoltat în 2009 și este acum o recomandare a W3C. WOFF este în esență OpenType sau TrueType cu compresie și metadate suplimentare. Scopul este de a sprijini distribuirea fontului de la un server la un client printr-o rețea cu restricții de lățime de bandă.
Web Open Font Format (WOFF 2.0)
Fontul TrueType / OpenType care asigură o compresie mai bună decât WOFF 1.0.
Fonturi / forme SVG
Fonturile SVG permit SVG-ului să fie utilizat ca glife la afișarea textului. Specificația SVG 1.1 definește un modul de font care permite crearea de fonturi într-un document SVG. Puteți aplica CSS și în documentele SVG, iar regula @ font-face poate fi aplicată textului în documente SVG.
Fonturi OpenType încorporate (EOT)
Fonturile EOT sunt o formă compactă de fonturi OpenType proiectate de Microsoft pentru a fi utilizate ca fonturi încorporate pe paginile web.
Asistență browser pentru formate de fonturi
IE: formatul fontului funcționează numai atunci când este setat să fie „instalabil”.
Firefox: Nu este acceptat implicit, dar poate fi activat (trebuie să setați un steag la „true” pentru a utiliza WOFF2).
Utilizarea Bold Text
Trebuie să adăugați o altă regulă @font-face care conține descriptori pentru text bold
Descriptori de fonturi CSS (CSS Font Descriptors)
CSS Transformări 2D
Transformări 2D CSS
Transformările CSS vă permit să vă deplasați, să rotiți, să scalați și să înlăturați elemente.
Proprietăți CSS: transform.
Asistență browser (Browser Support)
Numerele din tabel specifică prima versiune a browserului care acceptă integral proprietatea.
Prefixuri specifice browserului
Unele browsere mai vechi au nevoie de prefixe specifice (-ms- sau -webkit-) pentru a înțelege proprietățile de transformare 2D.
CSS Metode de transformare 2D
Cu proprietatea de transformare CSS puteți utiliza următoarele metode de transformare 2D: translate(), rotate(), scaleX(), scaleY(), scale(), skewX(), skewY(), skew(), matrix()
Metoda translate() mută un element din poziția sa curentă (în funcție de parametrii indicați pentru axa X și axa Y).
Metoda rotate() roteste un element în sensul acelor de ceasornic sau în sens contrar acelor de ceasornic, în conformitate cu un anumit grad.
Utilizarea valorilor negative va roti elementul în sensul acelor de ceasornic.
Metoda scale() crește sau scade dimensiunea unui element (în funcție de parametrii dați pentru lățime și înălțime).
Metoda scaleX() crește sau scade lățimea unui element.
Metoda scaleY() crește sau scade înălțimea unui element.
Metoda skewX() frânează un element de-a lungul axei X cu unghiul dat.
Metoda skewY() frânează un element de-a lungul axei Y de unghiul dat.
Metoda skew() frânează un element de-a lungul axelor X și Y de unghiurile date.
Metoda matrix() combină toate metodele de transformare 2D într-una.
Metoda matrix() ia șase parametri, care conțin funcții matematice, ceea ce vă permite să rotiți, să scalați, să mutați (să translați) și să înlăturați elemente.
Parametrii sunt următorii: matrix(scaleX(),skewY(),skewX(),scaleY(),translateX(),translateY())
Proprietăți de transformare CSS
transform - Aplică o transformare 2D sau 3D la un element.
transform-origin - Vă permite să schimbați poziția asupra elementelor transformate.
CSS Metode de transformare 2D
matrix(n, n, n, n, n, n) - Definește o transformare 2D, folosind o matrice de șase valori
translate(x, y) - Definește o transformare 2D, mutând elementul de-a lungul axei X și Y
translateX(n) - Definește o transformare 2D, mutând elementul de-a lungul axei X
translateY(n) - Definește o transformare 2D, mutând elementul de-a lungul axei Y
scale(x, y) - Definește o transformare la scară 2D, modificând lățimea și înălțimea elementelor
scaleX(n) - Definește o transformare la scară 2D, modificând lățimea elementului
scaleY(n) - Definește o transformare la scară 2D, schimbând înălțimea elementului
rotate(angle) - Definește o rotație 2D, unghiul este specificat în parametru
skew(angle x, angle y) - Definește o transformare în 2D de-a lungul axei X și Y
skewX(angle) - Definește o transformare în 2D de-a lungul axei X
skewY(angle) - Definește o transformare în 2D de-a lungul axei Y
CSS Transformări 3D
CSS Transformări 3D
CSS acceptă, de asemenea, transformări 3D.
În acest capitol veți afla despre următoarele proprietăți CSS: transform
Asistență browser (Browser Support)
Prefixuri specifice browserului
Unele browsere mai vechi au nevoie de prefixe specifice (-webkit-) pentru a înțelege proprietățiile de transformare 3D.
CSS Metode de transformare 3D
Cu proprietatea de transformare CSS puteți utiliza următoarele metode de transformare 3D: rotateX(), rotateY(), rotateZ()
Metoda rotateX() roteste un element in jurul axei X la un anumit grad.
Metoda rotateY() roteste un element in jurul axei sale Y la un anumit grad.
Metoda rotateZ() roteste un element in jurul axei Z la un anumit grad.
Proprietăți de transformare CSS
transform - Aplică o transformare 2D sau 3D la un element
transform-origin - Vă permite să schimbați poziția asupra elementelor transformate
transform-style - Specifică modul în care sunt redate elementele nested în spațiul 3D
perspective - Specifică perspectiva asupra modului în care sunt vizualizate elementele 3D
perspective-origin - Specifică poziția de jos a elementelor 3D
backface-visibility - Vizualizează dacă un element trebuie să fie vizibil atunci când nu este orientat către ecran
CSS Metode de transformare 3D
matrix3d
(n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n) - Definește o transformare 3D, folosind o matrice 4x4 cu 16 valori
translate3d(x, y, z) - Definește o traducere 3D
translateX(x) - Definește o traducere 3D, folosind doar valoarea pentru axa X
translateY(y) - Definește o traducere 3D, folosind doar valoarea pentru axa Y
translateZ(z) - Definește o traducere 3D, folosind doar valoarea pentru axa Z
scale3d(x, y, z) - Definește o transformare la scară 3D
scaleX(x) - Definește o transformare a scării 3D dând o valoare pentru axa X
scaleY(y) - Definește o transformare a scării 3D dând o valoare pentru axa Y
scaleZ(z) - Definește o transformare a scării 3D dând o valoare pentru axa Z
rotate3d(x, y, z, angle) - Definește o rotație 3D
rotateX(angle) - Definește o rotație 3D de-a lungul axei X
rotateY(angle) - Definește o rotație 3D de-a lungul axei Y
rotateZ(angle) - Definește o rotație 3D de-a lungul axei Z
perspective(n) - Definește o vedere în perspectivă pentru un element transformat 3D
CSS Tranziții
Tranziții CSS
Tranzițiile CSS vă permit să modificați valorile proprietății fără probleme, pe o durată dată.
În acest capitol veți afla despre următoarele proprietăți: transition, transition-delay, transition-duration, transition-property, transition-timing-function
Asistență browser pentru tranziții
Prefixuri specifice browserului
Unele browsere mai vechi au nevoie de prefixuri specifice (-webkit-) pentru a înțelege proprietățiile de tranziție
Cum se utilizează tranzițiile CSS?
Pentru a crea un efect de tranziție, trebuie să specificați două lucruri:
proprietatea CSS la care doriți să adăugați un efect
durata efectului
Dacă partea de durată nu este specificată, tranziția nu va avea nici un efect, deoarece valoarea implicită este 0.
Un element <div> 100px * 100px red. Elementul <div> a specificat, de asemenea, un efect de tranziție pentru proprietatea de lățime, cu o durată de 2 secunde.
Efectul de tranziție va începe atunci când proprietatea CSS (lățimea/width) specificată modifică valoarea.
Acum, să specificăm o nouă valoare pentru proprietatea de lățime/width atunci când un utilizator se alătură peste elementul <div>:
Atunci când cursorul se decuplează din element, acesta se va schimba treptat înapoi la stilul său original.
Modificați mai multe valori ale proprietății
Efect de tranziție atât pentru proprietatea lățimii (width), cât și pentru înălțime (height), cu o durată de 2 secunde pentru lățime (width) și 4 secunde pentru înălțime (height).
Specificați curba de viteză (speed curve) a tranziției
Proprietatea transition-timing-function specifică curba de viteză (speed curve) a efectului de tranziție.
Proprietatea transition-timing-function poate avea următoarele valori:
ease - specifică un efect de tranziție cu început lent, apoi rapid, apoi sfârșit lent (acest lucru este implicit)
linear - specifică un efect de tranziție cu aceeași viteză de la început până la sfârșit
ease-in - specifică un efect de tranziție cu pornire lentă
ease-out - specifică un efect de tranziție cu sfârșit lent
ease-in-out - specifică un efect de tranziție cu început și sfârșit lent
cubic-bezier(n,n,n,n) - vă permite să definiți propriile valori într-o funcție cub-bezier
Întârzie efectul de tranziție (Delay the Transition Effect)
Proprietatea transition-delay specifică o întârziere (în secunde) pentru efectul de tranziție.
Tranziție + transformare (Transition + Transformation)
Proprietățiile CSS transition pot fi specificate una câte una
Proprietatea shorthand transition
Proprietăți CSS transition:
transition - O proprietate scurtă pentru setarea celor patru proprietăți de tranziție într-o singură proprietate
transition-delay - Specifică o întârziere (în secunde) pentru efectul de tranziție
transition-duration - Specifică câte secunde sau milisecunde durează un efect de tranziție
transition-property - Specifică numele proprietății CSS pentru care este efectul de tranziție
transition-timing-function - Specifică curba de viteză a efectului de tranziție
CSS Animații
Animații CSS
CSS permite animarea elementelor HTML fără a utiliza JavaScript sau Flash!
În acest capitol veți afla despre următoarele proprietăți: @keyframes, animation-name, animation-duration, animation-delay, animation-iteration-count, animation-direction, animation-timing-function, animation-fill-mode, animation.
Asistență browser pentru animații (Browser Support for Animations)
Prefixuri specifice browserului
Unele browsere mai vechi au nevoie de prefixe specifice (-webkit-) pentru a înțelege proprietățiile de animație.
Ce sunt animațiile CSS?
O animație permite unui element să se schimbe treptat de la un stil la altul.
Puteți modifica câte proprietăți CSS doriți, de câte ori doriți.
Pentru a utiliza animația CSS, trebuie mai întâi să specificați câteva cadre cheie pentru animație.
Cadrele cheie conțin ce stiluri va avea elementul în anumite momente.
Regula @keyframes
Când specificați stiluri CSS din regula @keyframes, animația se va schimba treptat de la stilul curent la noul stil în anumite momente.
Pentru ca animația să funcționeze, trebuie să legați animația de un element.
Legarea animației „exemplu” de elementul <div>. Animația va dura 4 secunde și va schimba treptat culoarea de fundal a elementului <div> de la „red” la „yellow”.
Proprietatea animation-duration definește cât timp ar trebui să dureze o animație. Dacă proprietatea animation-duration nu este specificată, nu va apărea nicio animație, deoarece valoarea implicită este 0s (0 secunde).
Am specificat când stilul se va schimba folosind cuvintele cheie „from” și „to” (care reprezintă 0% (start) și 100% (complet)).
Este posibilă utilizarea procentului. Utilizând procente, puteți adăuga oricâte modificări de stil doriți.
Schimbarea culorii de fundal (background-color) a elementului <div> atunci când animația este completă 25%, 50% completă și din nou când animația este 100% completă:
Întârziere animație (Delay an Animation)
Proprietatea animation-delay specifică o întârziere pentru începerea unei animații.
De asemenea, sunt permise valori negative. Dacă utilizați valori negative, animația va începe ca și cum ar fi jucat deja N secunde.
Setați de câte ori ar trebui să ruleze o animație
Proprietatea animation-iteration-count specifică numărul pe care trebuie să-l ruleze o animație.
Valoarea „infinite” - pentru a face animația să continue pentru totdeauna
Rulați animația în direcție inversă sau cicluri alternative
Proprietatea animation-direction specifică dacă o animație trebuie să fie redată înainte, înapoi sau în cicluri alternative.
Proprietatea animation-direction poate avea următoarele valori:
normal - Animația este redată normal (înainte). Aceasta este implicită
reverse - animația este redată în sens invers (înapoi)
alternate - animația este redată mai întâi, apoi înapoi
alternate-reverse - animația este redată mai întâi înapoi, apoi înainte
Rulare animație în sens invers (înapoi)(backwards).
Valoarea "alternate" pentru a face ca animația să fie difuzată mai întâi înainte (forwards), apoi înapoi (backwards).
Valoarea „alternate-reverse” pentru a face ca animația să fie rulată mai întâi înapoi(backwards), apoi înainte (forwards)
Rulați animația în direcție inversă sau cicluri alternative
Proprietatea animation-direction specifică dacă o animație trebuie să fie redată înainte, înapoi sau în cicluri alternative.
Proprietatea animation-direction poate avea următoarele valori:
normal - Animația este redată normal (înainte)(forwards). Aceasta este implicită
reverse - animația este redată în sens invers (înapoi)
alternate - animația este redată mai întâi înainte(forwards), apoi înapoi(backwards)
alternate-reverse - animația este redată mai întâi înapoi(backwards), apoi înainte(forwards)
Rulare animație în sens invers (înapoi)(backwards):
Valoarea "alternate" pentru a face ca animația să fie difuzată mai întâi înainte (forwards), apoi înapoi (backwards).
Valoarea „alternate-reverse” pentru a face ca animația să fie rulată mai întâi înapoi(backwards), apoi înainte(forwards).
Precizați curba de viteză (Speed Curve) a animației
Proprietatea animation-timing-function specifică curba de viteză (speed curve) a animației.
Proprietatea animation-timing-function poate avea următoarele valori:
ease - Specifică o animație cu început lent, apoi rapid, apoi sfârșit încet (aceasta este implicit)
linear - Specifică o animație cu aceeași viteză de la început până la sfârșit
ease-in - Specifică o animație cu pornire lentă
ease-out - Specifică o animație cu sfârșit lent
ease-in-out - Specifică o animație cu început și sfârșit lent
cubic-bezier(n,n,n,n) - Vă permite să definiți propriile valori într-o funcție cubic-bezier
Precizați modul de completare (fill-mode) pentru o animație
Animațiile CSS nu afectează un element înainte de a fi redat primul cadru-cheie (keyframe) sau după ce ultimul cadru-cheie (keyframe) este redat. Proprietatea animation-fill-mode poate înlocui acest comportament.
Proprietatea animation-fill-mode specifică un stil pentru elementul țintă atunci când animația nu se joacă (înainte de a începe, după ce se termină, sau ambele).
Proprietatea animation-fill-modepoate avea următoarele valori:
none - Valoare implicită. Animația nu va aplica niciun stil la element înainte sau după executarea acestuia
forwards - Elementul va pastra valorile stilului setate de ultimul cadru cheie (keyframe) (depinde de animation-direction și animation-iteration-count)
backwards - Elementul va obține valorile de stil setate de primul cadru-cheie (keyframe) (depinde de animation-direction) și îl va păstra în timpul perioadei de întârziere a animației
both - Animația va respecta regulile atât în față cât și înapoi (forwards și backwards), extinzând proprietățiile de animație în ambele direcții
Elementul <div> păstrează valorile stilului de la ultimul cadru cheie (keyframe) la încheierea animației.
Exemple animation-fill-mode
Elementul <div> obține valorile style setate de primul cadru cheie (keyframe) înainte de începerea animației (în perioada de întârziere a animației (animation-delay)).
Elementul <div> obține valorile style setate de primul cadru cheie (keyframe) înainte de începerea animației și să păstreze valorile stilului de la ultimul cadru de cheie (keyframe) atunci când animația se încheie.
Proprietatea Shorthand Animation
Proprietăți CSS animation
@keyframes - Specifică codul de animație
animation - O proprietate shorthand pentru setarea tuturor proprietăților de animație
animation-delay - Specifică o întârziere pentru începerea unei animații
animation-direction - Specifică dacă o animație trebuie să fie redată înainte, înapoi sau în cicluri alternative
animation-duration - Specifică cât timp trebuie să dureze o animație pentru a finaliza un ciclu
animation-fill-mode - Specifică un stil pentru element atunci când animația nu se joacă (înainte de a începe, după ce se termină sau ambele)
animation-iteration-count - Specifică numărul de ori când trebuie să fie redată o animație
animation-name - Specifică numele animației @keyframes
animation-play-state - Specifică dacă animația este în curs de execuție sau în pauză
animation-timing-function - Specifică curba de viteză a animației
CSS Tooltip
CSS Tooltip
Creați tooltips cu CSS.
Un tooltip este adesea folosit pentru a specifica informații suplimentare despre ceva când utilizatorul mută indicatorul mouse-ului peste un element.
Basic Tooltip
Creați un tooltip care apare când utilizatorul mută mouse-ul peste un element.
HTML: Utilizați un element container (cum ar fi <div>) și adăugați-i clasa „tooltip”. Când utilizatorul trece cu mouse-ul peste acest <div>, va afișa textul de tip tooltip.
Textul de tip tooltip este plasat în interiorul unui element inline (cum ar fi <span>) cu class = "tooltiptext".
CSS: Clasa tooltip folosește position:relative, care este necesară pentru poziționarea textului tooltip (position:absolute).
Consultați exemplele de mai jos despre cum să poziționați indicatorul.
Clasa tooltiptext conține textul actual de tip tooltip. Este ascunsă în mod implicit și va fi vizibilă în hover (vezi mai jos). De asemenea, i-am adăugat câteva stiluri de bază: 120px lățime (width), culoare de fundal neagră, culoare text alb, text centrat (black background color, white text color, centered text) și 5px top și bottom padding.
Proprietatea CSS border-radius este utilizată pentru a adăuga colțuri rotunjite (rounded corners) tooltip text.
Selectorul :hover este utilizat pentru a afișa textul de tip tooltip atunci când utilizatorul mută mouse-ul peste <div> cu class="tooltip".
Positioning Tooltips
tooltip-ul este plasat la dreapta (left: 105%) a textului „hoverable” (<div>). De asemenea, rețineți că partea de sus:-5px (top:-5px) este utilizată pentru a-l plasa în mijlocul elementului container. Folosim numărul 5 deoarece textul de tip tooltip are o acoperire de 5px în partea de sus și de jos (top and bottom padding). Dacă măriți padding, creșteți și valoarea proprietății de top pentru a vă asigura că aceasta rămâne la mijloc (dacă este ceea ce doriți). Același lucru este valabil dacă doriți ca tooltip să fie plasat la stânga.
Dacă doriți ca tooltip să apară în partea de sus sau de jos ( top sau bottom), consultați exemplele de mai jos. Rețineți că folosim proprietatea margin-left cu o valoare de minus 60 pixeli. Acest lucru este pentru a centra tooltip deasupra/sub (above/below ) textul hoverable. Este setat la jumătatea lățimii tooltip-ului (120/2 = 60).
Instrumente săgeți (Tooltip Arrows)
Pentru a crea o săgeată (arrow) care ar trebui să apară dintr-o parte specifică a tooltip-ului, adăugați conținut „empty” după tooltip, cu pseudo-element class ::after împreună cu proprietatea content. Săgeata în sine este creată folosind borders. Acest lucru va face ca tooltip-ul să pară un speech bubble.
Adăugare săgeată la partea de jos a tooltip-ului.
Poziționarea săgeții în interiorul tooltip: top: 100% va așeza săgeata în partea de jos a tooltip. left: 50% va centra săgeata.
Proprietatea border-width specifică dimensiunea săgeții. Dacă schimbați acest lucru, modificați, de asemenea, valoarea margin-left. Aceasta va menține săgeata centrată.
Border-color este utilizată pentru a transforma conținutul într-o săgeată. Am stabilit top border la negru, iar restul la transparent. Dacă toate părțile ar fi negre, s-ar termina cu o black square box.
Adăugați o săgeată în partea de sus a tooltip.
Adăugați o săgeată la stânga tooltip-ului.
Adăugați o săgeată la dreapta tooltip-ului.
Fade In Tooltips (Animation)
Dacă doriți să aplicați fade în tooltip text când urmează să fie vizibil, puteți utiliza proprietatea CSS transition împreună cu proprietatea opacity și puteți trece de la a fi complet invizibil la 100% vizibil, într-un număr de secunde specificate (1 secundă în exemplul nostru).
CSS Stilizarea imaginilor
CSS Stilizarea imaginilor (CSS Styling Images)
Imagini rotunjite (Rounded Images)
Utilizați proprietatea border-radius pentru a crea imagini rotunjite (rounded images).
Imagini în miniatură (Thumbnail Images)
Utilizați proprietatea border pentru a crea imagini în miniatură (thumbnail images).
Imagine in miniatură (thumbnail image).
Imagine în miniatură ca link (Thumbnail Image as Link).
Imagini responsive (Responsive Images)
Imaginile responsive se vor regla automat pentru a se potrivi cu dimensiunea ecranului.
Redimensionați fereastra browserului pentru a vedea efectul.
Centrați o imagine (Center an Image)
Pentru a centra o imagine, setați marginea stângă și dreapta pe auto și transformați-o într-un element block.
Imagini / Carduri Polaroid (Polaroid Images / Cards)
Imagine transparentă
Proprietatea opacity poate lua o valoare între 0,0 și 1,0. Cu cât valoarea este mai mică, cu atât este mai transparentă:
IE8 și versiunile anterioare folosesc filter:alpha(opacity=x). X poate lua o valoare de la 0 la 100. O valoare mai mică face ca elementul să fie mai transparent.
Image Text
Cum se poziționează textul într-o imagine.
Filtre de imagine (Image Filters)
Proprietatea CSS filter adaugă efecte vizuale (precum estomparea și saturația/(blur and saturation) unui element.
Proprietatea CSS filter nu este acceptată în Internet Explorer, Edge 12 sau Safari 5.1 și nici în versiunile anterioare.
Image Hover Overlay
Creați un efect de suprapunere asupra hover.
Rotiți o imagine
Mutați mouse-ul peste imagine.
Galerie de imagini responsive
CSS poate fi utilizat pentru a crea galerii de imagini. Acest exemplu utilizează interogări media pentru a reorganiza imaginile pe dimensiuni de ecran diferite. Redimensionați fereastra browserului pentru a vedea efectul.
Image Modal (Advanced)
Modul în care CSS și JavaScript pot lucra împreună.
În primul rând, utilizați CSS pentru a crea o fereastră modală (dialog box) și ascundeți-o în mod implicit.
Apoi, utilizați un JavaScript pentru a afișa fereastra modală și pentru a afișa imaginea în interiorul modalului, atunci când un utilizator face click pe imagine.
CSS object-fit
Proprietatea CSS object-fit
Proprietatea CSS object-fit este utilizată pentru a specifica modul în care un <img> sau <video> trebuie redimensionat pentru a se potrivi cu containerul său.
Această proprietate spune conținutului să umple containerul într-o varietate de moduri; cum ar fi „păstrați acel raport de aspect” sau „întindeți-vă și ocupați cât mai mult spațiu”.
Asistență browser (Browser Support)
Avem două imagini și dorim ca acestea să umple lățimea de 50% a ferestrei browserului și 100% din înălțime.
Nu folosim object-fit, așa că atunci când redimensionăm fereastra browserului, raportul de aspect al imaginilor va fi distrus.
Folosim object-fit: cover; astfel, când redimensionăm fereastra browserului, raportul de aspect al imaginilor este păstrat.
Toate valorile proprietății CSS object-fit
Proprietatea CSS object-fit poate avea următoarele valori:
fill - Aceasta este implicită. Conținutul înlocuit este dimensionat pentru a completa content box a elementului. Dacă este necesar, obiectul va fi stretched sau squished pentru a se potrivi
contain - Conținutul înlocuit este scalat pentru a-și menține raportul de aspect (aspect ratio) în timp ce se încadrează în content box a elementului
cover - Conținutul înlocuit este dimensionat pentru a-și păstra raportul de aspect (aspect ratio) în timp ce umpleți întreaga content box a elementului. Obiectul va fi tăiat (clipped ) pentru a se potrivi
none - Conținutul înlocuit nu este redimensionat
scale-down - Conținutul este dimensionat ca și cum nici un conținut nu a fost specificat (ar avea ca rezultat o dimensiune mai mică a obiectului concret).
CSS Butoane
Butoane CSS
Aflați cum puteți stabili butoanele folosind CSS.
Stilarea butonului de bază (Basic Button Styling)
Culorile butoanelor (Button Colors)
Utilizați proprietatea background-color pentru a schimba culoarea de fundal a unui buton
Mărimea butoanelor (Button Sizes).
Utilizați proprietatea font-size pentru a modifica dimensiunea fontului unui buton.
Utilizați proprietatea padding pentru a schimba umplerea unui buton.
Butoane rotunjite (Rounded Buttons)
Utilizați proprietatea border-radius pentru a adăuga colțuri rotunjite la un buton.
Margini butoane colorate (Colored Button Borders)
Utilizați proprietatea border pentru a adăuga un chenar colorat la un buton
Butoane Hoverable
Utilizați selectorul :hover pentru a schimba stilul unui buton atunci când deplasați mouse-ul peste el.
Utilizați proprietatea transition pentru a determina viteza efectului „hover”.
Butoane Shadow
Utilizați proprietatea box-shadow pentru a adăuga umbre la un buton.
Butoane dezactivate (Disabled Buttons)
Utilizați proprietatea opacity pentru a adăuga transparență unui buton (creează un aspect „disabled”).
Puteți adăuga, de asemenea, proprietatea cursor cu o valoare „nepermisă” (not-allowed), care va afișa un „no parking sign” când faceți click peste buton.
Lățimea butonului (Button Width)
În mod implicit, dimensiunea butonului este determinată de conținutul textului său (la fel de larg ca și conținutul său). Utilizați proprietatea width pentru a modifica lățimea unui buton.
Grupuri de butoane (Button Groups)
Eliminați marginile și adăugați float:left la fiecare buton pentru a crea un grup de butoane.
Grup de butoane mărginite (Bordered Button Group)
Utilizați proprietatea border pentru a crea un grup de butoane mărginite.
Grup vertical de butoane (Vertical Button Group)
Utilizați display:block în loc de float:left pentru a grupa butoanele unul sub altul, în loc de alături
Buton pe imagine (Button on Image)
Adăugați un buton la o imagine.
Butoane animate (Animated Buttons)
Adăugați o săgeată la hover.
Adăugați un efect „apăsat” (pressed) pe click.
Fade in on hover.
Adăugați un efect „ripple” la click.
CSS Paginare
CSS Paginare
Aflați cum puteți crea o paginare responsive folosind CSS.
Paginare simplă
Dacă aveți un site web cu o mulțime de pagini, poate doriți să adăugați un fel de paginare la fiecare pagină.
Paginarea activă și hoverable
Evidențiați pagina curentă cu o clasă .active și folosiți selectorul :hover pentru a schimba culoarea fiecărei linii de pagină atunci când deplasați mouse-ul peste ele.
Butoane rotunjite active și hoverable
Dacă doriți un buton rotund „active” și „hover” adăugați proprietatea border-radius.
Efect de tranziție hoverable (Hoverable Transition Effect)
Adăugați proprietatea transition la link-urile paginii pentru a crea un efect de tranziție în timpul trecerii (hover).
Paginare mărginită (Bordered Pagination)
Utilizați proprietatea border pentru a adăuga borduri la paginație.
Margini rotunjite (Rounded Borders)
Adăugați rounded borders la prima și ultima dvs. legătură (link) din paginare.
Spațiu între legături (Space Between Links)
Adăugați proprietatea margin dacă nu doriți să grupați linkurile paginii.
Mărimea paginării (Pagination Size)
Modificați dimensiunea paginării cu proprietatea font-size.
Paginarea centrată (Centered Pagination)
Pentru a centra paginarea, wrap un element de tip container (cum ar fi <div>) în jurul lui cu text-align:center
Paginare Breadcrumbs
O altă variantă a paginării este așa-numita "breadcrumbs"
CSS Coloane multiple
CSS Coloane multiple
Layout cu mai multe coloane CSS( CSS Multi-column Layout)
Aspectul cu mai multe coloane CSS (multi-column layout) permite definirea ușoară a mai multor coloane de text - la fel ca în ziare.
Proprietăți CSS Multi-column
În acest capitol veți afla despre următoarele proprietăți CSS multi-column: column-count, column-gap, column-rule-style, column-rule-width, column-rule-color, column-rule, column-span, column-width.
Asistență browser (Browser Support)
CSS Creează mai multe coloane (CSS Create Multiple Columns)
Proprietatea column-count specifică numărul de coloane în care trebuie divizat un element.
Impărțirea textului din elementul <div> în 3 coloane.
CSS Specificați decalajul dintre coloane (CSS Specify the Gap Between Columns)
Proprietatea column-gap specifică decalajul dintre coloane.
Specifică o distanță de 40 de pixeli între coloane.
CSS Reguli coloane (CSS Column Rules)
Proprietatea column-rule-style specifică stilul regulii dintre coloane.
Proprietatea column-rule-width specifică lățimea regulii între coloane.
Proprietatea column-rule-color specifică culoarea regulii dintre coloane.
Proprietatea column-rule este o proprietate shorthand pentru setarea tuturor proprietăților column-rule- * de mai sus.
Stabilre lățimea, stilul și culoarea (width, style, color) regulii între coloane.
Specificați câte coloane ar trebui să se întindă (Specify How Many Columns an Element Should Span)
Proprietatea column-span specifică câte coloane ar trebui să se întindă (span) între un element.
Următorul exemplu specifică faptul că elementul <h2> ar trebui să se întindă (span) pe toate coloanele.
Specificați Lățimea coloanei (Specify The Column Width)
Proprietatea coloană-lățime specifică o lățime sugerată, optimă pentru coloane.
Specifică faptul că lățimea optimă sugerată pentru coloane ar trebui să fie de 100px.
Proprietăți CSS Multi-columns
column-count - Specifică numărul de coloane în care trebuie divizat un element
column-fill - Specifică modul de completare a coloanelor
column-gap - Specifică decalajul dintre coloane
column-rule - O proprietate shorthand pentru setarea tuturor proprietăților column-rule- *
column-rule-color - Specifică culoarea regulii dintre coloane
column-rule-style - Specifică stilul regulii dintre coloane
column-rule-width - Specifică lățimea regulii dintre coloane
column-span - Specifică câte coloane ar trebui să se întindă pe un element
column-width - Specifică o lățime sugerată, optimă pentru coloane
columns - O proprietate shorthand pentru setarea lățimii coloanei și a numărului de coloane
CSS Interfață utilizator
CSS Interfață utilizator
În acest capitol veți afla despre următoarele proprietăți ale interfeței de utilizator CSS: resize, outline-offset
Asistență browser
Numerele din tabel specifică prima versiune a browserului care acceptă integral proprietatea.
Redimensionare CSS (CSS Resizing)
Proprietatea resize specifică dacă (și cum) un element trebuie redimensionat de către utilizator.
Internet Explorer și Edge nu acceptă proprietatea resize.
Permite utilizatorului să redimensioneze doar lățimea unui element <div>.
Permite utilizatorului să redimensioneze doar înălțimea unui element <div>.
Permite utilizatorului redimensionarea atât a înălțimii, cât și a lățimii unui element <div>.
În multe browsere, <textarea> poate fi redimensionată în mod implicit. Aici, am folosit proprietatea resize pentru a dezactiva redimensionarea.
CSS Outline Offset
Proprietatea outline-offset adaugă spațiu între un contur (outline) și margine (edge) sau un border unui element.
Conturul (Outline) diferă de granițe (borders)! Spre deosebire de graniță (border), conturul (outline) este tras în afara graniței (border) elementului și poate suprapune alt conținut. De asemenea, conturul (outline) NU este o parte din dimensiunile elementului; lățimea și înălțimea (width și height) totală a elementului nu este afectată de lățimea conturului (outline).
Următorul exemplu utilizează proprietatea outline-offset pentru a adăuga spațiu între graniță (borders) și contur (outline)
Proprietăți CSS interfață utilizator
outline-offset - Adăugă spațiu între un contur (outline) și margine (edge) sau marginea (border) unui element
resize - Specifică dacă un element poate fi redimensionat de către utilizator
CSS Variabile
Variabile CSS
Proprietăți CSS personalizate (variabile)
Funcția var() poate fi utilizată pentru a insera valoarea unei proprietăți personalizate.
Asistență browser (Browser Support)
Numerele din tabel specifică prima versiune a browserului care acceptă integral proprietatea.
Funcția var()
Variabilele din CSS ar trebui declarate în cadrul unui selector CSS care definește domeniul său de aplicare. Pentru un domeniu global, puteți utiliza fie :root sau selectorul body.
Numele variabilei trebuie să înceapă cu două liniuțe (--) și este sensibil la litere mari și mici!
custom-name - Obligatoriu. Numele proprietății personalizate (trebuie să înceapă cu două liniuțe).
value - Opțional. Valoarea de retragere (folosită dacă proprietatea personalizată este nevalidă).
Definire proprietate personalizată globală numită "--main-bg-color", apoi folosire funcția var() pentru a insera valoarea proprietății personalizate ulterior în foaia de stil (style sheet):
CSS Funcția var()
var () - Inserează valoarea unei proprietăți custom
CSS Box Sizing
CSS Box Sizing
Proprietatea CSS box-sizing ne permite să includem padding și border în lățimea și înălțimea totală (width și height) a unui element.
Fără proprietatea CSS box-sizing
În mod implicit, lățimea și înălțimea (width și height) unui element sunt calculate astfel:
width + padding + border = lățimea reală a unui element
height + padding + border = înălțimea reală a unui element
Aceasta înseamnă: Când setați lățimea / înălțimea (width/height) unui element, elementul pare adesea mai mare decât ați setat (deoarece border-ul și padding-ul elementului sunt adăugate la lățimea / înălțimea (width/height) specificată a elementului).
Cu proprietatea CSS box-sizing
Proprietatea CSS box-sizing ne permite să includem padding și border în lățimea și înălțimea (width și height) totală a unui element.
Dacă setați box-sizing: border-box; pe un element padding și border sunt incluse în lățime și înălțime (width și height).
Deoarece rezultatul utilizării box-sizing: border-box; este cu atât mai bine, mulți dezvoltatori doresc ca toate elementele din paginile lor să funcționeze astfel.
Codul de mai jos asigură în acest mod mai intuitiv dimensiunea tuturor elementelor. Multe browsere folosesc deja box-sizing: border-box; pentru multe elemente de formă (dar nu toate - motiv pentru care inputs și text areas arată diferit la width: 100%;).
Aplicarea acestui lucru pe toate elementele este sigur și înțelept.
Proprietatea CSS Box Sizing
box-sizing - Defineste modul în care se calculează lățimea și înălțimea (width și height) unui element: trebuie să includă padding și borders, sau nu.
CSS Interogări media
CSS Interogări media (CSS Media Queries)
CSS2 Tipuri de suport introduse (CSS2 Introduced Media Types)
Regula @media, introdusă în CSS2, a făcut posibilă definirea regulilor de stil (style rules) diferite pentru diferite tipuri de media.
Ați putea avea un set de reguli de stil (style rules) pentru ecrane de computer, una pentru imprimante, una pentru dispozitive portabile, una pentru dispozitive tip televizor și așa mai departe.
Din păcate, aceste tipuri de suporturi nu au primit niciodată multă asistență din partea dispozitivelor, în afară de tipul de printare (print media type).
CSS3 Interogări media introduse (CSS3 Introduced Media Queries)
Interogările media (Media queries) din CSS3 au extins ideea tipurilor de media CSS2: În loc să caute un tip de dispozitiv, ele analizează capacitatea dispozitivului.
Interogările media (Media queries) pot fi utilizate pentru a verifica multe lucruri, cum ar fi:
lățimea și înălțimea vizualizării (width and height of the viewport)
lățimea și înălțimea dispozitivului (width and height of the device)
orientare (tableta / telefonul este în mod landscape sau portret?) (orientation (is the tablet/phone in landscape or portrait mode?))
rezoluţie (resolution)
Asistență browser(Browser Support)
Numerele din tabel specifică prima versiune a browserului care acceptă integral regula @media.
Sintaxa interogare media (Media Query Syntax)
O interogare media (media query) constă dintr-un tip media și poate conține una sau mai multe expresii, care se rezolvă returnand fie valoarea adevărat, fie valoarea fals.
Rezultatul interogării este adevărat dacă tipul de media (media type) specificat se potrivește cu tipul de dispozitiv pe care este afișat documentul și toate expresiile din interogarea media (media query) sunt adevărate. Când o interogare media (media query) este adevărată, se aplică foaia de stil (stylesheets) sau regulile de stil (style rules) corespunzătoare, urmând regulile normale în cascadă.
Cu excepția cazului în care utilizați operatorii not sau only, tipul media este opțional și tot tipul va fi implicat.
Puteți avea, de asemenea, foi de stil (stylesheets) diferite pentru media diferite.
CSS3 Tipuri media (CSS3 Media Types)
all - Utilizat pentru toate dispozitivele de tip media
print - Utilizat pentru imprimante
screen - Utilizat pentru ecrane, tablete, telefoane inteligente etc.
speach - Utilizată pentru ecranizatorii care „citesc” pagina cu voce tare
O modalitate de a utiliza interogări media (media queries) este să aveți o secțiune CSS alternativă chiar în foaia de stil (style sheet).
CSS Flexbox
CSS Flexbox
CSS Modulul Flexbox Layout (CSS Flexbox Layout Module)
Înainte de modulul Layout Flexbox, existau patru moduri de aspect:
Block, pentru secțiunile dintr-o pagină web
Inline, pentru text
Table, pentru date în două dimensiuni ale tabelului
Positioned, pentru poziția explicită a unui element
Flexible Box Layout Module, face mai ușoară proiectarea unei structuri flexibile layout responsive fără a folosi float sau poziționare (positioning).
Asistență browser(Browser Support)
Proprietățilie flexbox sunt acceptate în toate browserele moderne.
Elemente Flexbox (Flexbox Elements)
Pentru a începe să utilizați modelul Flexbox, trebuie să definiți mai întâi un recipient flex (flex container).
Elementul de mai sus reprezintă un recipient flex (flex container) (zona albastră) cu trei elemente flexibile.
Un container flex cu trei articole flexibile.
O dispunere flexibilă (Flexible Layout) trebuie să aibă un element părinte cu proprietatea de afișare setată la flex.
Elementele directe ale copilului ale containerului flexibil devin automat elemente flexibile.
Proprietățiile containerului flex sunt: flex-direction, flex-wrap, flex-flow, justify-content, align-items, align-content.
Proprietatea flex-direction
Proprietatea flex-direction definește în ce direcție containerul dorește să stiveze elementele flex.
"flex-direction: column;" stivuiește elementele flexate vertical (de sus în jos).
Valoarea coloanei (column) stochează vertical elementele flex (de sus în jos).
Valoarea coloană-inversă (column-reverse) stochează vertical elementele flex (dar de jos în sus).
Valoarea row-reverse stochează elementele flexate pe orizontală (dar de la dreapta la stânga).
Proprietatea flex-wrap specifică dacă elementele flex trebuie să fie wrap sau nu.
Valoarea wrap specifică faptul că elementele flex se vor wrap dacă este necesar.
Valoarea nowrap specifică faptul că elementele flex nu se vor wrap (aceasta este implicită).
Valoarea wrap-reverse specifică faptul că elementele flexibile se vor wrap dacă este necesar, în ordine inversă.
Proprietatea flex-flow este o proprietate shorthand pentru setarea proprietăților flex-direction și flex-wrap.
Proprietatea justify-content este utilizată pentru alinierea elementelor flex
Valoarea center aliniază elementele flex în centrul containerului
Valoarea flex-start aliniază elementele flex la începutul containerului (implicit)
Valoarea flex-end aliniază elementele flex la sfârșitul containerului
Valoarea space-around afișează elementele flex cu spațiu înainte, între și după linii (before, between și after)
Valoarea space-between afișează elementele flexibile cu spațiu între linii
Proprietatea align-items este utilizată pentru alinierea elementelor flexate pe verticală.
Utilizăm un container înalt de 200 de pixeli, pentru a demonstra mai bine proprietatea align-items.
Valoarea center aliniază elementele flex din mijlocul containerului.
Valoarea flex-start aliniază elementele flex din partea de sus a containerului.
Valoarea flex-end aliniază elementele flex din partea de jos a containerului.
Valoarea stretch întinde elementele flex pentru a umple containerul (aceasta este implicit).
Valoarea baseline aliniază elementele flex, cum ar fi alinierea lor de bază.
Proprietatea align-content este utilizată pentru a alinia liniile flex.
În aceste exemple, utilizăm un container înalt de 600 de pixeli, cu proprietatea flex-wrap setată pentru a wrapa, pentru a demonstra mai bine proprietatea align-content.
Valoarea space-between afișează liniile flexate cu spațiu egal între ele.
Valoarea space-around afișează liniile flexate cu spațiu înainte, între și după ele.
Valoarea stretch întinde liniile flex pentru a ocupa spațiul rămas (acesta este implicit).
Valoarea center afișează liniile de flexare din mijlocul containerului.
Valoarea flex-start afișează liniile flex la începutul containerului.
Valoarea flex-end afișează liniile de flex la sfârșitul containerului.
Centrare perfectă
În următorul exemplu, vom rezolva o problemă de stil foarte comună: centrarea perfectă (perfect centering).
Setați atât proprietățiile justify-content, cât și align-items in centru, iar elementul flex va fi perfect centrat.
Child Elements (Items)
Elementele child directe ale unui recipient flex devin automat elemente flexibile (flexibile).
Proprietățiile elementului flex: order, flex-grow, flex-shrink, flex-basis, flex, align-self.
Proprietatea order specifică ordinea elementelor flex.
Primul element flex din cod nu trebuie să apară ca primul element din layout.
Valoarea order trebuie să fie un număr, valoarea implicită este 0.
Proprietatea order poate modifica ordinea articolelor flex.
Proprietatea flex-grow specifică cât de mult va crește un element flex în raport cu restul elementelor flex.
Valoarea flex-grow trebuie să fie un număr, valoarea implicită este 0.
Faceți ca cel de-al treilea element flex să crească de opt ori mai rapid decât celelalte elemente flex.
Proprietatea flex-shrink specifică cât de mult se va micsora un element flex în raport cu restul elementelor flex.
Valoarea flex-shrink trebuie să fie un număr, valoarea implicită este 1.
Nu lăsați al treilea element flex să se micșoreze la fel de mult decât celelalte elemente flex.
Proprietatea flex-basis specifică lungimea inițială a unui element flex.
Proprietatea flex este o proprietate shorthand pentru proprietățiile flex-grow, flex-shrink și flex-basis.
Proprietatea align-self specifică alinierea pentru elementul selectat în interiorul containerului flexibil.
Proprietatea align-self înlocuiește alinierea setată implicit de proprietatea align-items a containerului.
Galerie de imagini responsive folosind Flexbox
Utilizați flexbox pentru a crea o galerie de imagini responsive care variază între patru, două sau imagini cu lățime completă, în funcție de dimensiunea ecranului.
Website responsive folosind Flexbox
Utilizați flexbox pentru a crea un responsive website, care conține o bară de navigare flexibilă și conținut flexibil.
Proprietăți CSS Flexbox
display - Specifică tipul de box folosit pentru un element HTML
flex-direction - Specifică direcția articolelor flexibile din interiorul unui recipient flex
justify-content - Aliniază orizontal elementele flex atunci când elementele nu folosesc tot spațiul disponibil pe axa principală
align-items - Aliniază vertical elementele flex atunci când elementele nu folosesc tot spațiul disponibil pe axa transversală
flex-wrap - Specifică dacă elementele flexate trebuie să se înfășoare (wrap) sau nu, dacă nu există suficient loc pentru ele pe o singură linie flex
align-content - Modifică comportamentul proprietății flex-wrap. Este similar cu align-items, dar în loc să alinieze elementele flex, aliniază liniile flex
flex-flow - O proprietate shorthand pentru flex-direction și flex-wrap
order - Specifică ordinea unui articol flexibil în raport cu restul elementelor flexibile din interiorul aceluiași recipient
align-self - Folosit pe articolele flex. Înlocuiește proprietatea align-items
flex - O proprietate shorthand pentru proprietățile flex-grow, flex-shrink și flex-basis
CSS Interogări media - Exemple
Interogări media CSS - exemple
Interogările media sunt o tehnică populară pentru livrarea unei foi de stil adaptate diferitelor dispozitive. Pentru a demonstra un exemplu simplu, putem schimba culoarea de fundal pentru diferite dispozitive.
Interogări media pentru meniuri
În acest exemplu, folosim interogări media pentru a crea un meniu de navigare responsive, care variază în ceea ce privește designul pe diferite dimensiuni de ecran.
Interogări media pentru coloane
O utilizare obișnuită a interogărilor media este de a crea un aspect flexibil (flexible layout). În acest exemplu, creem un aspect (layout) care variază între patru, două și full-width coloane, în funcție de diferitele dimensiuni ale ecranului.
Un mod mai modern de a crea column layouts este să folosiți CSS Flexbox. Cu toate acestea, nu este acceptat în Internet Explorer 10 și versiunile anterioare. Dacă aveți nevoie de asistență IE6-10, folosiți floats.
Ascundeți elementele cu interogări media
O altă utilizare obișnuită a interogărilor media este de a ascunde elemente pe diferite dimensiuni ale ecranului.
Modificați dimensiunea fontului cu interogări media
De asemenea, puteți utiliza interogări media pentru a modifica dimensiunea fontului (font size) unui element pe diferite dimensiuni ale ecranului.
Galerie de imagini flexibile
Folosim interogări media împreună cu flexbox pentru a crea o galerie de imagini responsive.
Site web flexibil
Utilizăm interogări media împreună cu flexbox pentru a crea un site web responsive, care conține o bară de navigare flexibilă și conținut flexibil.
Orientare: Portret / Peisaj
Interogările media pot fi, de asemenea, utilizate pentru a schimba aspectul (layout) unei pagini, în funcție de orientarea browserului.
Puteți avea un set de proprietăți CSS care se vor aplica numai atunci când fereastra browserului este mai largă decât înălțimea sa, o așa-numită orientare „Peisaj” (Landscape):
Utilizați o culoare de fundal lightblue (background color) dacă orientarea este în modul peisaj (landscape):
Folosind o valoare suplimentară: adăugăm o interogare media suplimentară la cea existentă folosind virgulă (aceasta se va comporta ca un operator OR).
CSS Responsive Web Design - Introducere
Responsive Web Design - Introducere
Ce este Responsive Web Design?
Responsive web design face ca pagina dvs. web să arate bine pe toate dispozitivele.
Responsive web design utilizează numai HTML și CSS.
Responsive web design nu este un program sau un JavaScript.
Proiectarea pentru cea mai bună experiență pentru toți utilizatorii
Paginile web pot fi vizualizate folosind mai multe dispozitive diferite: desktop-uri, tablete și telefoane. Pagina dvs. web ar trebui să arate bine și să fie ușor de utilizat, indiferent de dispozitiv.
Paginile web nu ar trebui să lase informații pentru a se potrivi cu dispozitive mai mici, ci mai degrabă să își adapteze conținutul pentru a se potrivi cu orice dispozitiv.
CSS Responsive Web Design - Viewport
Responsive Web Design - Viewport
Ce este Viewport?
Viewport este zona vizibilă a utilizatorului unei pagini web.
Viewportul variază în funcție de dispozitiv și va fi mai mic pe un telefon mobil decât pe un ecran al computerului.
Înainte de tablete și telefoane mobile, paginile web erau concepute doar pentru ecranele computerului și era comun ca paginile web să aibă un design static și o dimensiune fixă.
Apoi, când am început să navigăm pe internet folosind tablete și telefoane mobile, paginile web cu dimensiuni fixe erau prea mari pentru a se potrivi cu ecranul. Pentru a remedia acest lucru, browserele de pe aceste dispozitive au redus întreaga pagină web pentru a se potrivi ecranului.
Nu a fost perfect !! Dar o rezolvare rapidă.
Setarea Viewport
HTML5 a introdus o metodă pentru a permite proiectanților web să preia controlul asupra viewport-ului, prin intermediul etichetei <meta>.
Ar trebui să includeți următorul element viewport <meta> în toate paginile dvs. web.
Un element viewport <meta> oferă instrucțiuni browserului cu privire la modul de control al dimensiunilor și scalării paginii.
width=device-width part stabilește lățimea paginii pentru a urma lățimea ecranului dispozitivului (screen-width) (care va varia în funcție de dispozitiv).
initial-scale=1.0 setează nivelul inițial de zoom atunci când pagina este încărcată prima dată de browser.
Iată un exemplu de pagină web fără viewport meta tag și aceeași pagină web cu viewport meta tag.
Mărimea conținutului la Viewport (Size Content to The Viewport)
Utilizatorii sunt folosiți pentru a derula site-urile pe verticală atât pe desktop cât și pe dispozitive mobile - dar nu pe orizontală!
Așadar, dacă utilizatorul este obligat să defileze orizontal sau să mărească, pentru a vedea întreaga pagină web, rezultă o experiență slabă a utilizatorului.
Câteva reguli suplimentare de urmat:
NU folosiți elemente cu lățime fixă mare - De exemplu, dacă o imagine este afișată la o lățime mai largă decât cea din portofoliu, aceasta poate determina derularea portofoliului pe orizontală. Nu uitați să ajustați acest conținut pentru a se încadra în lățimea vizualizării.
NU lăsați conținutul să se bazeze pe o anumită lățime a viewportului (viewport width) pentru a fi redat - Deoarece dimensiunile ecranului și lățimea în pixeli CSS variază foarte mult între dispozitive, conținutul nu ar trebui să se bazeze pe o anumită lățime a viewportului pentru a fi redat.
Utilizați interogări CSS media (media queries) pentru a aplica stiluri diferite pentru ecrane mici și mari - Setarea lățimilor CSS mari pentru elementele paginii va face ca elementul să fie prea larg pentru viewport de pe un dispozitiv mai mic. În schimb, luați în considerare utilizarea unor valori de lățime relative, cum ar fi lățimea: 100%. De asemenea, aveți grijă să folosiți valori mari de poziționare absolută. Poate determina elementul să iasă în afara ecranului pe dispozitive mici.
CSS Responsive Web Design - Grid-View
Responsive Web Design - Grid-View
Ce este un Grid-View?
Multe pagini web se bazează pe un grid-view, ceea ce înseamnă că pagina este împărțită în coloane.
Un responsive grid-view are adesea 12 coloane și are o lățime totală de 100% și se va micsora și se va extinde pe măsură ce redimensionați fereastra browserului.
Construirea unui responsive Grid-View
Vom începe să construim un responsive Grid-View.
Mai întâi asigurați-vă că toate elementele HTML au proprietatea box-sizing setată pe border-box. Acest lucru asigură că padding și border sunt incluse în lățimea totală și înălțimea (total width and height) elementelor.
CSS Responsive Web Design - Interogări media
Responsive Web Design - Interogări media
Ce este o interogare media?
Interogarea media este o tehnică CSS introdusă în CSS3.
Utilizează regula @media pentru a include un block de proprietăți CSS numai dacă o anumită condiție este adevărată.
Dacă fereastra browserului este de 600px sau mai mică, culoarea de fundal (background color) va fi deschisă la culoare (lightblue).
Adăugați un Breakpoint
Mai devreme în acest tutorial am făcut o pagină web cu rânduri și coloane și a fost responzive, dar nu arăta bine pe un ecran mic.
Interogările media (media queries) vă pot ajuta. Putem adăuga un punct de break (breakpoint) unde anumite părți ale designelui se vor comporta diferit pe fiecare parte a punctului de break (breakpoint).
Utilizați o interogare media (media queries) pentru a adăuga un punct de break (breakpoint) la 768px:
Când ecranul (fereastra browserului) devine mai mic decât 768px, fiecare coloană ar trebui să aibă o lățime de 100%.
Întotdeauna design pentru mobil întâi
Mobile First înseamnă proiectare pentru mobil înainte de proiectare pentru desktop sau orice alt dispozitiv (Acest lucru va face afișarea paginii mai rapidă pe dispozitive mai mici).
Aceasta înseamnă că trebuie să facem unele modificări în CSS-ul nostru.
În loc să schimbăm stilurile când lățimea devine mai mică de 768px, ar trebui să schimbăm designul când lățimea devine mai mare de 768px. Acest lucru va face în primul rând proiectarea noastră mobilă.
Puteți adăuga câte breakpoints doriți.
Vom insera, de asemenea, un punct de break (breakpoint) între tablete și telefoane mobile.
Facem acest lucru prin adăugarea a încă o interogare media (media query ) (la 600px) și un set de clase noi pentru dispozitive mai mari de 600px (dar mai mici decât 768px):
Rețineți că cele două seturi de clase sunt aproape identice, singura diferență este denumirea (col- și col-s-).
Breakpoints tipice dispozitivului (Typical Device Breakpoints)
Există tone de ecrane și dispozitive cu înălțimi și lățimi diferite, așa că este greu să creezi un punct de break (breakpoint) exact pentru fiecare dispozitiv. Pentru a menține lucrurile simple, puteți viza cinci grupuri.
Orientare: Portret / Peisaj (Landscape)
Interogările media (media queries) pot fi, de asemenea, utilizate pentru a schimba aspectul (layout) unei pagini, în funcție de orientarea browserului.
Puteți avea un set de proprietăți CSS care se vor aplica numai atunci când fereastra browserului este mai largă decât înălțimea sa, o așa-numită orientare „Peisaj” (Lanscape):
Pagina web va avea un fundal luminos (lightblue background) dacă orientarea este în modul peisaj (lanscape).
Ascundeți elementele cu interogări media (Hide Elements With Media Queries)
O altă utilizare obișnuită a interogărilor media (media queries) este de a ascunde elemente pe dimensiuni diferite de ecran.
Modificați dimensiunea fontului cu interogări media (Change Font Size With Media Queries)
De asemenea, puteți utiliza interogări media (media queries) pentru a modifica dimensiunea fontului unui element pe diferite dimensiuni ale ecranului.
CSS Responsive Web Design - Imagini
Responsive Web Design - Images
Utilizarea proprietății Width
Dacă proprietatea lățimii (width) este setată la un procent și înălțimea este setată la „auto”, imaginea va fi receptivă și va scala în sus și în jos.
Imaginea poate fi redusă pentru a fi mai mare decât dimensiunea inițială. O soluție mai bună, în multe cazuri, va fi utilizarea în schimb a proprietății cu lățimea maximă.
Imaginile de fundal (Background Images) pot răspunde, de asemenea, la redimensionare și scalare (resizing și scaling).
Dacă proprietatea background-size este setată pe „contain”, imaginea de fundal (background Images) se va scala și va încerca să se potrivească zonei de conținut. Cu toate acestea, imaginea își va păstra raportul de aspect (relația proporțională între lățimea și înălțimea imaginii (width și height)).
Dacă proprietatea background-size este setată pe „100% 100%”, imaginea de fundal (background image) se va întinde pentru a acoperi întreaga zonă de conținut.
Dacă proprietatea background-size este setată pe „cover”, imaginea de fundal (background image) se va scala pentru a acoperi întreaga zonă de conținut. Observați că valoarea „cover” păstrează raportul de aspect (aspect ratio), iar o parte din imaginea de fundal (background image) poate fi tăiată.
Imagini diferite pentru dispozitive diferite
O imagine mare poate fi perfectă pe un ecran mare al unui computer, dar inutilă pe un dispozitiv mic. De ce să încărcați o imagine mare atunci când trebuie să o măriți în jos? Pentru a reduce încărcarea sau pentru orice alte motive, puteți utiliza interogări media (media queries) pentru a afișa imagini diferite pe dispozitive diferite.
Puteți utiliza interogarea media (media query) min-device-width, în loc de min-width, care verifică lățimea dispozitivului, în loc de lățimea browserului. Atunci imaginea nu se va schimba când redimensionați fereastra browserului.
Elementul HTML5 <picture>
HTML5 a introdus elementul <picture>, care vă permite să definiți mai multe imagini.
Asistență browser (Browser Support)
Elementul <picture> funcționează similar cu elementele <video> și <audio>. Configurați surse diferite, iar prima sursă care se potrivește preferințelor este cea utilizată:
Atributul srcset este necesar și definește sursa imaginii.
Atributul media este opțional și acceptă interogările media (media queries) pe care le găsiți în regula CSS @media.
De asemenea, ar trebui să definiți un element <img> pentru browserele care nu acceptă elementul <picture>.
CSS Responsive Web Design - Videoclipuri
Responsive Web Design - Videoclipuri
Utilizarea proprietății width
Dacă proprietatea lățimii (width) este setată la 100%, playerul video va răspunde și va scala în sus și în jos.
Rețineți că, playerul video poate fi amplificat pentru a fi mai mare decât dimensiunea inițială. O soluție mai bună, în multe cazuri, va fi utilizarea în schimb a proprietății cu lățimea maximă (max-width).
Utilizarea proprietății lățime maximă (max-width)
Dacă proprietatea lățime maximă (max-width) este setată la 100%, playerul video va scădea în jos dacă trebuie, dar niciodată nu va fi mai mare decât dimensiunea inițială.
Adăugați un videoclip la pagina web de exemplu
Vrem să adăugăm un videoclip în pagina noastră web de exemplu. Videoclipul va fi redimensionat pentru a ocupa întotdeauna tot spațiul disponibil.
CSS Responsive Web Design - Frameworks
Responsive Web Design - Frameworks
Există multe CSS Frameworks existente care oferă un design responsive.
Sunt gratuite și ușor de utilizat.
Folosire W3.CSS
O modalitate excelentă de a crea un design responsive este să folosești o foaie de stil responsive ( responsive style sheet), cum ar fi W3.CSS
W3.CSS facilitează dezvoltarea site-urilor care arată frumos la orice dimensiune; desktop, laptop, tabletă sau telefon.
Bootstrap
Un alt framework popular este Bootstrap, folosește HTML, CSS și jQuery pentru a face pagini web responsive.
CSS Grid Introducere
CSS Grid Layout Module
Grid Layout
CSS Grid Layout Module oferă un sistem de dispunere bazat pe grilă, cu rânduri și coloane, ceea ce facilitează proiectarea paginilor web fără a fi nevoie să folosiți plutitoare și poziționare (floats și positioning).
Asistență browser(Browser Support)
Proprietățiile grid sunt acceptate în toate browserele moderne.
Elemente grid
Un layout grid este format dintr-un element părinte, cu unul sau mai multe elemente copil.
Proprietatea display
Un element HTML devine un container grid atunci când proprietatea sa display este setată pe grid sau în inline-grid.
Toți copiii direcți (direct children) ai containerului grid devin automat elemente grid.
Coloane Grid (Grid Columns)
Liniile verticale ale elementelor grid se numesc coloane (columns).
Rânduri Grid (Grid Rows)
Liniile orizontale ale elementelor grid se numesc rânduri (rows).
Grid Gaps
Spațiile dintre fiecare coloană/rând (column/row) se numesc gaps.
Puteți ajusta dimensiunea gapului folosind una dintre următoarele proprietăți:grid-column-gap, grid-row-gap, grid-gap.
Proprietatea grid-column-gap stabilește diferența dintre coloane.
Proprietatea grid-row-gap stabilește diferența dintre rânduri.
Proprietatea grid-gap este o proprietate shorthand pentru proprietățile grid-column-gap și grid-row-gap.
Proprietatea grid-gap poate fi, de asemenea, folosită pentru a seta atât row gap cât și column gap într-o singură valoare.
Linii Grid (Grid Lines)
Liniile dintre coloane se numesc linii coloană (column lines).
Liniile dintre rânduri se numesc linii rând (row lines).
Consultați numerele de linie atunci când introduceți un element grid într-un container grid.
Plasați un element grid la linia coloanei 1 și lăsați-o să se încheie pe linia 3 a coloanei.
Plasați un element grid la linia 1 de rând și lăsați-o să se încheie pe linia 3 de rând.
CSS Grid Container
Grid Container
Pentru a face ca un element HTML să se comporte ca un container grid, trebuie să setați proprietatea display la grid sau la inline-grid.
Containerele grid constau din elemente grid, plasate în coloane și rânduri (columns și rows).
Proprietatea grid-template-columns
Proprietatea grid-template-columns definește numărul de coloane din aspectul gridului dvs. (grid layout) și poate defini lățimea (width) fiecărei coloane.
Valoarea este un space-separated-list, unde fiecare valoare definește lungimea coloanei respective.
Dacă doriți ca aspectul gridului (grid layout) să conțină 4 coloane, specificați lățimea (width) celor 4 coloane sau „auto” dacă toate coloanele trebuie să aibă aceeași lățime (width).
Proprietatea grid-template-rows definește înălțimea (height) fiecărui rând (row).
Valoarea este un space-separated-list, unde fiecare valoare definește înălțimea (height) rândului respectiv (row).
Proprietatea justify-content este utilizată pentru alinierea întregului grid în interiorul containerului.
Lățimea (width) totală a gridului trebuie să fie mai mică decât lățimea (width) containerului pentru ca proprietatea justify-content să aibă vreun efect.
Proprietatea align-content este utilizată pentru alinierea verticală (vertically align) a întregului grid în interiorul containerului.
Înălțimea (height) totală a gridului trebuie să fie mai mică decât înălțimea (height) containerului pentru ca proprietatea align-content să aibă vreun efect.
CSS Grid Item
CSS Grid Item
Child Elements (Items)
Un container grid conține elemente grid.
În mod implicit, un container are un articol grid pentru fiecare coloană, în fiecare rând, dar puteți stila elementele gridului astfel încât acestea să se întindă pe mai multe coloane și / sau rânduri.
Proprietatea grid-column:
Proprietatea grid-column definește pe ce coloane (ele) să plaseze un articol.
Definiți unde va începe elementul și unde se va termina.
Proprietatea grid-column este o proprietate shorthand pentru proprietățiile grid-column-start și grid-column-end.
Pentru a plasa un articol, vă puteți referi la numere de linie sau puteți utiliza cuvântul cheie „span” pentru a defini câte coloane va cuprinde.
Proprietatea grid-row
Proprietatea grid-row definește pe ce rând să plaseze un element.
Definiți unde va începe elementul și unde se va termina.
Proprietatea grid-row este o proprietate shorthand pentru proprietățiile grid-row-start și grid-row-end.
Pentru a plasa un articol, vă puteți referi la numere de linie sau puteți utiliza cuvântul cheie „span” pentru a defini câte rânduri va cuprinde elementul.
Proprietatea grid-area
Proprietatea grid-area poate fi utilizată ca proprietate de tip shorthand pentru proprietățiile grid-row-start, grid-column-start, grid-row-end și the grid-column-end.
Denumirea elementelor grid
Proprietatea grid-area poate fi, de asemenea, utilizată pentru a atribui nume elementelor grid.
Elementele grid denumite (Named grid items) pot fi menționate de proprietatea grid-template-areas ale containerului grid.
Fiecare rând este definit prin apostroafe ('')
Coloanele din fiecare rând sunt definite în interiorul apostrofelor, separate de un spațiu.
Un semn de perioadă reprezintă un element grid fără nume.
Pentru a defini două rânduri, definiți coloana celui de-al doilea rând în interiorul unui alt set de apostroafe.
The Order of the Items
Aspectul gridului (Grid Layout) ne permite să poziționăm articolele oriunde ne-ar plăcea.
Primul articol din codul HTML nu trebuie să apară ca prim element din grid.
SQL Introducere
Introducere în SQL
SQL este un limbaj standard pentru accesarea și manipularea bazelor de date.
Ce este SQL?
SQL înseamnă limbaj de interogare structurat
SQL vă permite să accesați și să manipulați bazele de date
SQL a devenit un standard al American National Standards Institute (ANSI) în 1986 și al Organizației Internaționale pentru Standardizare (ISO) în 1987
Ce poate face SQL?
SQL poate executa interogări împotriva unei baze de date
SQL poate prelua date dintr-o bază de date
SQL poate insera înregistrări într-o bază de date
SQL poate actualiza înregistrările într-o bază de date
SQL poate șterge înregistrările dintr-o bază de date
SQL poate crea baze de date noi
SQL poate crea tabele noi într-o bază de date
SQL poate crea proceduri stocate într-o bază de date
SQL poate crea vizualizări într-o bază de date
SQL poate seta permisiunile pe tabele, proceduri și vizualizări
SQL este un Standard - DAR ....
Deși SQL este un standard ANSI / ISO, există diferite versiuni ale limbajului SQL.Cu toate acestea, pentru a respecta standardul ANSI, toate acceptă cel puțin comenzile majore (cum ar fi SELECT, UPDATE, DELETE, INSERT, WHERE) într-o manieră similară.
Majoritatea programelor bazei de date SQL au și extensii proprii în plus față de standardul SQL.
Utilizarea SQL pe site-ul dvs. Web
Pentru a construi un site web care arată datele dintr-o bază de date, veti avea nevoie de:
Un program de bază de date RDBMS (adică MS Access, SQL Server, MySQL)
Pentru a utiliza un limbaj de script din partea serverului, cum ar fi PHP sau ASP
Pentru a utiliza SQL pentru a obține datele dorite
Pentru a utiliza HTML / CSS pentru stilul paginii
RDBMS reprezintă sistemul relațional de gestionare a bazelor de date.
RDBMS este baza pentru SQL și pentru toate sistemele de baze de date moderne precum MS SQL Server, IBM DB2, Oracle, MySQL și Microsoft Access.
Datele din RDBMS sunt stocate în obiectele bazei de date numite tabele. Un tabel este o colecție de intrări de date asociate și este format din coloane și rânduri.
Fiecare tabel este împărțit în entități mai mici numite câmpuri. Câmpurile din tabelul Clienți constau din CustomerID, CustomerName, ContactName, Adresa, Oraș, Cod Postal și Țară. Un câmp este o coloană dintr-un tabel concepută pentru a păstra informații specifice despre fiecare înregistrare din tabel.
O înregistrare, numită și rând, este fiecare intrare individuală care există într-un tabel. De exemplu, există 91 de înregistrări în tabelul Clienților de mai sus. O înregistrare este o entitate orizontală dintr-un tabel.
O coloană este o entitate verticală dintr-un tabel care conține toate informațiile asociate cu un câmp specific dintr-un tabel.
SQL Sintaxă
Sintaxa SQL
Tabele de baze de date (Database Tables)
O bază de date conține cel mai adesea una sau mai multe tabele. Fiecare tabel este identificat printr-un nume (de exemplu, „Clienți” sau „Comenzi”). Tabelele conțin înregistrări (rânduri) cu date.
În acest tutorial vom folosi bine-cunoscuta bază de date de exemplu Northwind (inclusă în MS Access și MS SQL Server).
Selecție din tabelul „Clienți”.
Tabelul conține cinci înregistrări (una pentru fiecare client) și șapte coloane (CustomerID, CustomerName, ContactName, Address, City, PostalCode și Country).
Instrucțiuni SQL
Majoritatea acțiunilor pe care trebuie să le efectuați într-o bază de date sunt efectuate cu instrucțiuni SQL.
Ține minte că...
Cuvintele cheie SQL NU sunt sensibile la majuscule și minuscule (nu sunt case sensitive): selectarea este identică cu SELECT
În acest tutorial vom scrie toate cuvintele cheie SQL cu majuscule.
Semicolon după Instrucțiuni SQL?
Unele sisteme de baze de date necesită punct și virgulă la sfârșitul fiecărei instrucțiuni SQL.
Semicolon este modul standard de a separa fiecare instrucțiune SQL în sistemele de baze de date care permit executarea a mai mult de o instrucțiune SQL în același apel către server.
În acest tutorial, vom folosi punct și virgulă la sfârșitul fiecărei instrucțiuni SQL.
Unele dintre cele mai importante comenzi SQL
SELECT - extrage date dintr-o bază de date
UPDATE - actualizează datele dintr-o bază de date
DELETE - șterge datele dintr-o bază de date
INSERT INTO - introduce date noi într-o bază de date
CREATE DATABASE - creează o nouă bază de date
ALTER DATABASE - modifică o bază de date
CREATE TABLE - creează un nou tabel
ALTER TABLE - modifică un tabel
DROP TABLE - șterge un tabel
CREATE INDEX - creează un index (cheie de căutare)
DROP INDEX - șterge un index
SQL SELECT
SQL Select
Instrucțiunea SQL SELECT
Instrucțiunea SELECT este utilizată pentru a selecta date dintr-o bază de date.
Datele returnate sunt stocate într-un tabel de rezultate, numit set de rezultate (result-set).
Sintaxa SELECT
SQL SELECT DISTINCT
Instrucțiunea SQL SELECT DISTINCT
Instrucțiunea SELECT DISTINCT este utilizată pentru a returna doar valori distincte (diferite).
În interiorul unui tabel, o coloană conține adesea multe valori duplicate; și uneori doriți doar să enumerați valorile diferite (distincte).
SELECT DISTINCT Sintaxa
SELECT DISTINCT column1, column2, ...
FROM table_name;
Exemplu SELECT fără DISTINCT
Următoarea instrucțiune SQL selectează TOATE (inclusiv duplicatele) valorile din coloana „Country” din tabelul „Customers”:
SELECT Country FROM Customers;
Acum, să folosim cuvântul cheie DISTINCT cu instrucțiunea SELECT de mai sus și să vedem rezultatul.
Exemple SELECT DISTINCT
Următoarea instrucțiune SQL selectează numai valorile DISTINCT din coloana „Country” din tabelul „Customers”:
SELECT DISTINCT Country FROM Customers;
Următoarea instrucțiune SQL listează numărul de țări client (customer countries) diferite (distincte):
SELECT COUNT(DISTINCT Country) FROM Customers;
Exemplul de mai sus nu va funcționa în Firefox și Microsoft Edge! Deoarece COUNT (DISTINCT column_name) nu este acceptat în bazele de date Microsoft Access. Firefox și Microsoft Edge folosesc Microsoft Access în exemplele noastre.
Iată soluția pentru MS Access:
SELECT Count(*) AS DistinctCountries
FROM (SELECT DISTINCT Country FROM Customers);
SQL WHERE
Clauza SQL WHERE
Clauza WHERE este folosită pentru a filtra înregistrările.
Clauza WHERE este utilizată pentru a extrage doar acele înregistrări care îndeplinesc o condiție specificată.
Sintaxa WHERE
SELECT column1, column2, ...
FROM table_name
WHERE condition;
Clauza WHERE nu este utilizată numai în instrucțiunea SELECT, ci este utilizată și în instrucțiunea UPDATE, DELETE etc.
Exemplu de clauză WHERE
Următoarea declarație SQL selectează toți clienții din țara „Mexic”, în tabelul „Customers”:
SELECT * FROM Customers
WHERE Country='Mexic';
Text Fields vs. Numeric Fields
SQL necesită citate unice în jurul valorilor de text (majoritatea sistemelor de baze de date vor permite, de asemenea, ghilimele duble).
Cu toate acestea, câmpurile numerice nu trebuie incluse între ghilimele:
SELECT * FROM Customers
WHERE CustomerID=1;
Operatori în clauza WHERE
În clauza WHERE pot fi folosiți următorii operatori:
= Egal
> Mai mare decât
< Mai mic decât
> = Mai mare sau egal
<= Mai mic sau egal
<> Nu este egal. Notă: În unele versiuni de SQL, acest operator poate fi scris ca !=
BETWEEN - Între un anumit interval
LIKE - Căutați un model
IN - Pentru a specifica mai multe valori posibile pentru o coloană
SQL AND, OR și NOT
Operatorii SQL AND, OR și NOT
Clauza WHERE poate fi combinată cu operatorii AND, OR și NOT.
Operatorii AND și OR sunt folosiți pentru a filtra înregistrările pe baza mai multor condiții:
Operatorul AND afișează o înregistrare dacă toate condițiile separate de AND sunt TRUE.
Operatorul OR afișează o înregistrare dacă oricare dintre condițiile separate de OR este TRUE.
Operatorul NOT afișează o înregistrare dacă condițiile (condițiile) sunt NOT TRUE.
Sintaxa AND
SELECT column1, column2, ...
FROM table_name
WHERE condition1 AND condition2 AND condition3 ...;
Sintaxa OR
SELECT column1, column2, ...
FROM table_name
WHERE condition1 OR condition2 OR condition3 ...;
Sintaxa NOT
SELECT column1, column2, ...
FROM table_name
WHERE NOT condition;
Exemple SQL AND, OR și NOT
Exemplu AND
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers” unde țara este „Germania” AND orașul este „Berlin”:
SELECT * FROM Customers
WHERE Country='Germania' AND City='Berlin';
Exemplu OR
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers” unde orașul este „Berlin” OR „Munchen”:
SELECT * FROM Customers
WHERE City='Berlin' OR City='Munchen';
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers” unde țara este „Germania” OR „Spania”:
SELECT * FROM Customers
WHERE Country='Germania' OR Country='Spania';
Exemplu NOT
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers” în care țara NOT este „Germania”:
SELECT * FROM Customers
WHERE NOT Country='Germania';
Combinarea operatorilor AND, OR și NOT
Puteți combina, de asemenea, operatorii AND, OR și NOT.
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers" unde țara este „Germania” AND orașul trebuie să fie „Berlin” OR „Munchen” (folosiți paranteza pentru a forma expresii complexe):
SELECT * FROM Customers
WHERE Country='Germania' AND (City='Berlin' OR City='Munchen');
Următoarea instrucțiune SQL selectează toate câmpurile din „Customers" în care țara NOT este „Germania” și NOT „SUA”:
SELECT * FROM Customers
WHERE NOT Country='Germania' AND NOT Country='USA';
SQL ORDER BY
Cuvântul cheie SQL ORDER BY
Cuvântul cheie ORDER BY este utilizat pentru a sorta setul de rezultate (result-set) în ordine crescătoare sau descendentă.
Cuvântul cheie ORDER BY sortează înregistrările în ordine crescătoare în mod implicit. Pentru a sorta înregistrările în ordine descrescătoare, utilizați cuvântul cheie DESC.
Sintaxa ORDER BY
SELECT column1, column2, ...
FROM table_name
ORDER BY column1, column2, ... ASC|DESC;
Exemplu ORDER BY
Următoarea instrucțiune SQL selectează toți clienții din tabelul "Customers", ordonați după coloana „Country”:
SELECT * FROM Customers
ORDER BY Country;
Exemplu ORDER BY DESC
Următoarea instrucțiune SQL selectează toți clienții din tabelul "Customers", ordonați DESCENDING după coloana „Country”:
SELECT * FROM Customers
ORDER BY Country DESC;
Exemplu câteva coloane ORDER BY
Următoarea instrucțiune SQL selectează toți clienții din tabelul "Customers", sortați după coloana „Country” și „CustomerName”. Acest lucru înseamnă că se comandă după Country, dar dacă unele rânduri au același Country, atunci se comandă prin CustomerName:
SELECT * FROM Customers
ORDER BY Country, CustomerName;
Exemplu 2 - Câteva coloane ORDER BY
Următoarea instrucțiune SQL selectează toți clienții din tabelul „Customers”, sortați în ordine crescătoare după „Country” și descendenți după coloana „CustomerName”:
SELECT * FROM Customers
ORDER BY Country ASC, CustomerName DESC;
SQL INSERT INTO
Instrucțiunea SQL INSERT INTO
Instrucțiunea INSERT INTO este utilizată pentru a insera înregistrări noi într-un tabel.
Sintaxa INSERT INTO
Este posibil să scrieți instrucțiunea INSERT INTO în două moduri.
Prima modalitate specifică atât numele coloanelor, cât și valorile care trebuie introduse:
INSERT INTO table_name (column1, column2, column3, ...)
VALUES (value1, value2, value3, ...);
Dacă adăugați valori pentru toate coloanele tabelului, nu este necesar să specificați numele coloanelor din interogarea SQL. Cu toate acestea, asigurați-vă că ordinea valorilor este în aceeași ordine cu coloanele din tabel.
Sintaxa INSERT INTO ar fi următoarea:
INSERT INTO table_name
VALUES (value1, value2, value3, ...);
Exemplu INSERT INTO
Următoarea instrucțiune SQL introduce o nouă înregistrare în tabelul "Customers":
INSERT INTO Customers (CustomerName, ContactName, Address, City, PostalCode, Country)
VALUES ('Cardinal', 'Tom B. Erichsen', 'Skagen 21', 'Stavanger', '4006', 'Norway');
Inserați date numai în coloane specificate
De asemenea, este posibil să inserați date doar în coloane specifice.
Următoarea instrucțiune SQL va insera o înregistrare nouă, dar va insera doar date în coloanele „CustomerName”, „City” și „Country” (CustomerID va fi actualizat automat):
INSERT INTO Customers (CustomerName, City, Country)
VALUES ('Cardinal', 'Stavanger', 'Norway');
SQL Valori NULL
Valori SQL NULL
Un câmp cu o valoare NULL este un câmp fără nici o valoare.
Dacă un câmp dintr-un tabel este opțional, este posibil să inserați o înregistrare nouă sau să actualizați o înregistrare fără a adăuga o valoare la acest câmp. Apoi, câmpul va fi salvat cu o valoare NULL.
O valoare NULL este diferită de o valoare zero sau un câmp care conține spații. Un câmp cu o valoare NULL este unul care a fost lăsat liber în timpul creării înregistrărilor!
Nu este posibil să se testeze valorile NULL cu operatori de comparație, cum ar fi =, < sau <>.
În schimb, va trebui să utilizăm operatorii IS NULL și IS NOT NULL.
Sintaxa IS NULL
SELECT column_names
FROM table_name
WHERE column_name IS NULL;
Sintaxa IS NOT NULL
SELECT column_names
FROM table_name
WHERE column_name IS NOT NULL;
Operatorul IS NULL
Operatorul IS NULL este utilizat pentru testarea valorilor goale (valori NULL).
Următorul SQL listează toți clienții cu o valoare NULL în câmpul „Address”:
SELECT CustomerName, ContactName, Address
FROM Customers
WHERE Address IS NULL;
Folosiți întotdeauna IS NULL pentru a căuta valorile NULL.
Operatorul IS NOT NULL
Operatorul IS NOT NULL este utilizat pentru testarea valorilor care nu sunt goale (valori IS NOT NULL).
Următorul SQL listează toți clienții cu o valoare în câmpul „Address”:
SELECT CustomerName, ContactName, Address
FROM Customers
WHERE Address IS NOT NULL;
SQL UPDATE
Instrucțiunea SQL UPDATE
Instrucțiunea UPDATE este utilizată pentru a modifica înregistrările existente într-un tabel.
Sintaxa UPDATE
UPDATE table_name
SET column1 = value1, column2 = value2, ...
WHERE condition;
Aveți grijă când actualizați înregistrările într-un tabel! Observați clauza WHERE din declarația UPDATE. Clauza WHERE specifică ce înregistrări trebuie actualizate. Dacă omiteți clauza WHERE, toate înregistrările din tabel vor fi actualizate!
Tabela UPDATE
Următoarea instrucțiune SQL actualizează primul client (CustomerID = 1) cu o persoană de contact nouă și un oraș nou.
UPDATE Customers
SET ContactName = 'Ion Popescu', City= 'Bucuresti'
WHERE CustomerID = 1;
Înregistrări multiple UPDATE
Clauza WHERE este cea care determină câte înregistrări vor fi actualizate.
Următoarea declarație SQL va actualiza numele de contact la „Ion” pentru toate înregistrările în care țara este „Romania”:
UPDATE Customers
SET ContactName='Ion'
WHERE Country='Romania';
UPDATE avertizare!
Aveți grijă când actualizați înregistrările. Dacă omiteți clauza WHERE, TOATE înregistrările vor fi actualizate!
UPDATE Customers
SET ContactName='Ion';
SQL DELETE
Instrucțiunea SQL DELETE
Instrucțiunea DELETE este utilizată pentru a șterge înregistrările existente dintr-un tabel.
Sintaxa DELETE
DELETE FROM table_name WHERE condition;
Aveți grijă când ștergeți înregistrările dintr-un tabel! Observați clauza WHERE din declarația DELETE. Clauza WHERE specifică ce înregistrări trebuie eliminate. Dacă omiteți clauza WHERE, toate înregistrările din tabel vor fi șterse!
Exemplu SQL DELETE:
Următoarea instrucțiune SQL șterge clientul „Ion Popescu” din tabelul „Customers”:
DELETE FROM Customers WHERE CustomerName='Ion Popescu';
Ștergeți toate înregistrările
Este posibil să ștergeți toate rândurile dintr-un tabel fără a șterge tabelul. Aceasta înseamnă că structura tabelului, atributele și indexurile vor fi intacte:
DELETE FROM table_name;
Următoarea instrucțiune SQL șterge toate rândurile din tabelul „Customers”, fără a șterge tabelul:
DELETE FROM Customers;
SQL TOP, LIMIT sau ROWNUM
Clauzele SQL TOP, LIMIT sau ROWNUM
Clauza SQL SELECT TOP
Clauza SELECT TOP este utilizată pentru a specifica numărul de înregistrări de returnat.
Clauza SELECT TOP este utilă pe tabele mari cu mii de înregistrări. Restituirea unui număr mare de înregistrări poate afecta performanța.
Nu toate sistemele de baze de date acceptă clauza SELECT TOP. MySQL acceptă clauza LIMIT pentru a selecta un număr limitat de înregistrări, în timp ce Oracle utilizează ROWNUM.
Sintaxa SQL Server / MS Access
SELECT TOP number|percent column_name(s)
FROM table_name
WHERE condition;
Sintaxa MySQL
SELECT column_name(s)
FROM table_name
WHERE condition
LIMIT number;
Sintaxa Oracle
SELECT column_name(s)
FROM table_name
WHERE ROWNUM <= number;
Exemple SQL TOP, LIMIT și ROWNUM
Următoarea instrucțiune SQL selectează primele trei înregistrări din tabelul „Customers”:
SELECT TOP 3 * FROM Customers;
Următoarea instrucțiune SQL arată exemplul echivalent folosind clauza LIMIT:
SELECT * FROM Customers
LIMIT 3;
Următoarea instrucțiune SQL arată exemplul echivalent folosind ROWNUM:
SELECT * FROM Customers
WHERE ROWNUM <= 3;
Exemplu SQL TOP PERCENT
Următoarea instrucțiune SQL selectează primele 50% de înregistrări din tabelul „Customers”:
SELECT TOP 50 PERCENT * FROM Customers;
Adăugați o clauză WHERE
Următoarea declarație SQL selectează primele trei înregistrări din tabelul „Customers”, unde țara este „Germania”:
SELECT TOP 3 * FROM Customers
WHERE Country='Germania';
Următoarea instrucțiune SQL arată exemplul echivalent folosind clauza LIMIT:
SELECT * FROM Customers
WHERE Country='Germany'
LIMIT 3;
Următoarea instrucțiune SQL arată exemplul echivalent folosind clauza ROWNUM:
SELECT * FROM Customers
WHERE Country='Germania' AND ROWNUM <= 3;
SQL MIN() și MAX()
Funcțiile SQL MIN() și MAX()
Funcția MIN() returnează cea mai mică valoare a coloanei selectate.
Funcția MAX() returnează cea mai mare valoare a coloanei selectate.
Sintaxa MIN()
SELECT MIN(column_name)
FROM table_name
WHERE condition;
Sintaxa MAX()
SELECT MAX(column_name)
FROM table_name
WHERE condition;
Exemplu MIN()
Următoarea declarație SQL găsește prețul celui mai ieftin produs:
SELECT MIN(Price) AS SmallestPrice
FROM Products;
Exemplu MAX()
Următoarea declarație SQL găsește prețul celui mai scump produs:
SELECT MAX(Price) AS LargestPrice
FROM Products;
SQL COUNT(), AVG() și SUM()
Funcțiile SQL COUNT(), AVG() și SUM()
Funcția COUNT() returnează numărul de rânduri care corespund unui criteriu specificat.
Funcția AVG() returnează valoarea medie a unei coloane numerice.
Funcția SUM() returnează suma totală a unei coloane numerice.
Sintaxa COUNT()
SELECT COUNT(column_name)
FROM table_name
WHERE condition;
Sintaxa AVG()
SELECT AVG(column_name)
FROM table_name
WHERE condition;
Sintaxa SUM()
SELECT SUM(column_name)
FROM table_name
WHERE condition;
Exemplu COUNT()
Următoarea instrucțiune SQL găsește numărul de produse:
SELECT COUNT(ProductID)
FROM Products;
Valorile NULL nu sunt numărate.
Exemplu AVG()
Următoarea declarație SQL găsește prețul mediu al tuturor produselor:
SELECT AVG(Price)
FROM Products;
Valorile NULL sunt ignorate.
Exemplu SUM()
Următoarea instrucțiune SQL găsește suma câmpurilor „Quantity” din tabelul „OrderDetails”:
SELECT SUM(Quantity)
FROM OrderDetails;
Valorile NULL sunt ignorate.
SQL LIKE
Operatorul SQL LIKE
Operatorul LIKE este folosit într-o clauză WHERE pentru a căuta un model specificat într-o coloană.
Există două wildcards folosite adesea împreună cu operatorul LIKE:
% - Semnul procentual reprezintă zero, unu sau mai multe caractere
_ - Sublinierea reprezintă un singur personaj
MS Access folosește un asterisc (*) în loc de semnul procentual (%) și un semn de întrebare (?) În loc de subliniere (_).
Semnul procentual și sublinierea pot fi de asemenea utilizate în combinații!
Sintaxa LIKE
SELECT column1, column2, ...
FROM table_name
WHERE columnN LIKE pattern;
Puteți combina, de asemenea, orice număr de condiții folosind operatorii AND sau OR.
Iată câteva exemple care arată diferiți operatori LIKE cu wildcard-uri „%” și „_”:
WHERE CustomerName LIKE 'a%' - Găsește toate valorile care încep cu „a”
WHERE CustomerName LIKE '%a' - Găsește orice valori care se termină cu "a"
WHERE CustomerName LIKE '%or%' - Găsește orice valori care au „sau” în orice poziție
WHERE CustomerName LIKE '_r%' - Găsește orice valori care au „r” în a doua poziție
WHERE CustomerName LIKE 'a__%' - Găsește orice valori care încep cu „a” și au cel puțin 3 caractere în lungime
WHERE ContactName LIKE 'a%o' - Găsește orice valori care încep cu "a" și se termină cu "o"
Exemple SQL LIKE
Următoarea instrucțiune SQL selectează toți clienții cu un nume client începând cu „a”:
SELECT * FROM Customers
WHERE CustomerName LIKE 'a%';
Următoarea instrucțiune SQL selectează toți clienții cu un nume client care se termină cu „a”:
SELECT * FROM Customers
WHERE CustomerName LIKE '%a';
Următoarea instrucțiune SQL selectează toți clienții cu un nume client care au „or” în orice poziție:
SELECT * FROM Customers
WHERE CustomerName LIKE '%or%';
Următoarea instrucțiune SQL selectează toți clienții cu un nume client care are „r” în a doua poziție:
SELECT * FROM Customers
WHERE CustomerName LIKE '_r%';
Următoarea instrucțiune SQL selectează toți clienții cu un nume client care începe cu „a” și are cel puțin 3 caractere în lungime:
SELECT * FROM Customers
WHERE CustomerName LIKE 'a__%';
Următoarea instrucțiune SQL selectează toți clienții cu un nume de contact care începe cu „a” și se termină cu „o”:
SELECT * FROM Customers
WHERE ContactName LIKE 'a%o';
Următoarea instrucțiune SQL selectează toți clienții cu un nume client care NU începe cu „a”:
SELECT * FROM Customers
WHERE CustomerName NOT LIKE 'a%';
SQL Wildcards
SQL Wildcards
Caracterele SQL Wildcards
Un caracter wildcard este folosit pentru a substitui unul sau mai multe caractere dintr-un șir.
Caracterele wildcard sunt utilizate cu operatorul SQL LIKE. Operatorul LIKE este folosit într-o clauză WHERE pentru a căuta un model specificat într-o coloană.
Caractere wildcard în MS Access
* - Reprezintă zero sau mai multe caractere: bl* finds bl, black, blue and blob
? - Reprezintă un singur caracter: h?t finds hot, hat, and hit
[] - Reprezintă orice caracter dintre paranteze: h[oa]t finds hot and hat, but not hit
! - Reprezintă orice caracter care nu se află între paranteze: h[!oa]t finds hit, but not hot and hat
- - Reprezintă o serie de caractere: c[a-b]t finds cat and cbt
# - Reprezintă orice singur caracter numeric: 2#5 finds 205, 215, 225, 235, 245, 255, 265, 275, 285, and 295
Caractere wildcard în SQL Server:
% - Reprezintă zero sau mai multe caractere: bl% finds bl, black, blue, and blob
_ - Reprezintă un singur caracter: h_t finds hot, hat, and hit
[] - Reprezintă orice caracter dintre paranteze: h[oa]t finds hot and hat, but not hit
^ - Reprezintă orice caracter care nu se află între paranteze: h[^oa]t finds hit, but not hot and hat
- - Reprezintă o serie de caractere: c[a-b]t finds cat and cbt
Toate wildcards-urile pot fi, de asemenea, utilizate în combinații!
Iată câteva exemple care arată diferiți operatori LIKE cu wildcard-uri „%” și „_”:
WHERE CustomerName LIKE 'a%' - Găsește orice valoarecare începe cu „a”
WHERE CustomerName LIKE '%a' - Găsește orice valoare care se termină cu "a"
WHERE CustomerName LIKE '%or%' - Găsește orice valoare care are „or” în orice poziție
WHERE CustomerName LIKE '_r%' - Găsește orice valoare care are „r” în a doua poziție
WHERE CustomerName LIKE 'a_%_%' - Găsește orice valoare care începe cu „a” și are cel puțin 3 caractere în lungime
WHERE ContactName LIKE 'a%o' - Găsește orice valoare care începe cu "a" și se termină cu "o"
Utilizarea Wildcardului %
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care începe cu „ber”:
SELECT * FROM Customers
WHERE City LIKE 'ber%';
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care conține patternul "es":
SELECT * FROM Customers
WHERE City LIKE '%es%';
Folosirea Wildcardului _
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care începe cu orice caracter, urmată de „ondon”:
SELECT * FROM Customers
WHERE City LIKE '_ondon';
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care începe cu „L”, urmat de orice caracter, urmat de „n”, urmat de orice caracter, urmat de „on”:
SELECT * FROM Customers
WHERE City LIKE 'L_n_on';
Utilizarea wildcard-ului [charlist]
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care începe cu „b”, „s” sau „p”:
SELECT * FROM Customers
WHERE City LIKE '[bsp]%';
Următoarea instrucțiune SQL selectează toți clienții cu un oraș care începe cu „a”, „b” sau „c”:
SELECT * FROM Customers
WHERE City LIKE '[a-c]%';
Utilizarea wildcard-ului [!charlist]
Următoarele două instrucțiuni SQL selectează toți clienții cu un oraș care NOT (NU) începe cu "b", "s" sau "p":
SELECT * FROM Customers
WHERE City LIKE '[!bsp]%';
sau:
SELECT * FROM Customers
WHERE City NOT LIKE '[bsp]%';
SQL IN
Operatorul SQL IN
Operatorul IN vă permite să specificați mai multe valori într-o clauză WHERE.
Operatorul IN este un manual pentru mai multe condiții.
Sintaxa IN
SELECT column_name(s)
FROM table_name
WHERE column_name IN (value1, value2, ...);
sau:
SELECT column_name(s)
FROM table_name
WHERE column_name IN (SELECT STATEMENT);
Exemple de operator IN
Următoarea declarație SQL selectează toți clienții care se află în „Germania”, „Franța” sau „Marea Britanie”:
SELECT * FROM Customers
WHERE Country IN ('Germania', 'Franța', 'Marea Britanie');
Următoarea instrucțiune SQL selectează toți clienții care nu se află în „Germania”, „Franța” sau „Marea Britanie”:
SELECT * FROM Customers
WHERE Country NOT IN ('Germania', 'Franța”', 'Marea Britanie');
Următoarea instrucțiune SQL selectează toți clienții care provin din aceleași țări ca furnizorii:
SELECT * FROM Customers
WHERE Country IN (SELECT Country FROM Suppliers);
SQL BETWEEN
Operatorul SQL BETWEEN
Operatorul BETWEEN selectează valorile dintr-un interval dat. Valorile pot fi numere, text sau date (numbers, text sau dates).
Operatorul BETWEEN este inclus: valorile de început (begin) și de sfârșit (end) sunt incluse.
Sintaxa BETWEEN
SELECT column_name(s)
FROM table_name
WHERE column_name BETWEEN value1 AND value2;
Exemplu BETWEEN
Următoarea instrucțiune SQL selectează toate produsele cu un preț BETWEEN 10 și 20:
SELECT * FROM Products
WHERE Price BETWEEN 10 AND 20;
Exemplu NOT BETWEEN
Pentru a afișa produsele în afara intervalului din exemplul precedent, utilizați NOT BETWEEN:
SELECT * FROM Products
WHERE Price NOT BETWEEN 10 AND 20;
Exemplu BETWEEN cu IN
Următoarea instrucțiune SQL selectează toate produsele cu un preț BETWEEN 10 și 20. În plus; (addition;) nu afișați produse cu o CategoryID de 1,2 sau 3:
SELECT * FROM Products
WHERE Price BETWEEN 10 AND 20
AND NOT CategoryID IN (1,2,3);
Exemplu BETWEEN Text Values
Următoarea instrucțiune SQL selectează toate produsele cu un ProductName BETWEEN Carnarvon Tigers și Mozzarella di Giovanni:
SELECT * FROM Products
WHERE ProductName BETWEEN 'Carnarvon Tigers' AND 'Mozzarella di Giovanni'
ORDER BY ProductName;
Următoarea instrucțiune SQL selectează toate produsele cu un ProductName BETWEEN Carnarvon Tigers și Chef Anton's Cajun Seasoning:
SELECT * FROM Products
WHERE ProductName BETWEEN "Carnarvon Tigers" AND "Chef Anton's Cajun Seasoning"
ORDER BY ProductName;
Exemplu NOT BETWEEN Text Values
Următoarea instrucțiune SQL selectează toate produsele cu un ProductName NOT BETWEEN Carnarvon Tigers și Mozzarella di Giovanni:
SELECT * FROM Products
WHERE ProductName NOT BETWEEN 'Carnarvon Tigers' AND 'Mozzarella di Giovanni'
ORDER BY ProductName;
Exemplu BETWEEN Dates
Următoarea instrucțiune SQL selectează toate comenzile cu o OrderDate BETWEEN '01-July-1996' și '31-July-1996':
SELECT * FROM Orders
WHERE OrderDate BETWEEN #01/07/1996# AND #31/07/1996#;
sau
SELECT * FROM Orders
WHERE OrderDate BETWEEN '1996-07-01' AND '1996-07-31';
SQL Alias
Alias-urile SQL
Alias-urile SQL sunt utilizate pentru a da un nume temporar unei tabele sau unei coloane dintr-un tabel.
Alias-urile sunt adesea folosite pentru a face citirea numelor de coloane.
Un alias există doar pe durata interogării.
Sintaxa Coloanei Alias
SELECT column_name AS alias_name
FROM table_name;
Alias Table Syntax
SELECT column_name(s)
FROM table_name AS alias_name;
Exemple Alias pentru coloane
Următoarea instrucțiune SQL creează două alias-uri, unul pentru coloana CustomerID și unul pentru coloana CustomerName:
SELECT CustomerID AS ID, CustomerName AS Customer
FROM Customers;
Următoarea instrucțiune SQL creează două alias-uri, unul pentru coloana CustomerName și unul pentru coloana ContactName.
Este nevoie de ghilimele duble sau paranteze pătrate dacă numele alias conține spații:
SELECT CustomerName AS Customer, ContactName AS [Contact Person]
FROM Customers;
Următoarea instrucțiune SQL creează un alias numit „Address” care combină patru coloane (adresă, cod poștal, oraș și țară/Address, PostalCode, City and Country):
SELECT CustomerName, Address + ', ' + PostalCode + ' ' + City + ', ' + Country AS Address
FROM Customers;
Pentru ca instrucțiunea SQL de mai sus să funcționeze în MySQL, utilizați următoarele:
SELECT CustomerName, CONCAT(Address,', ',PostalCode,', ',City,', ',Country) AS Address
FROM Customers;
Exemplu Alias pentru tabele
Următoarea instrucțiune SQL selectează toate comenzile de la client cu CustomerID = 4 (Around the Horn). Folosim tabelele „Customers” și „Orders” și le oferim aliasul tabelului „c” și respectiv „o” (Aici folosim alias-uri pentru a face SQL-ul mai scurt):
SELECT o.OrderID, o.OrderDate, c.CustomerName
FROM Customers AS c, Orders AS o
WHERE c.CustomerName="Around the Horn" AND c.CustomerID=o.CustomerID;
Următoarea instrucțiune SQL este aceeași ca mai sus, dar fără alias:
SELECT Orders.OrderID, Orders.OrderDate, Customers.CustomerName
FROM Customers, Orders
WHERE Customers.CustomerName="Around the Horn" AND Customers.CustomerID=Orders.CustomerID;
Alias-urile pot fi utile atunci când:
Există mai multe tabele implicate într-o interogare
Funcțiile sunt utilizate în interogare
Numele coloanelor sunt mari sau nu sunt foarte citibile
Două sau mai multe coloane sunt combinate între ele
SQL JOIN
SQL JOIN
O clauză JOIN este utilizată pentru a combina rânduri din două sau mai multe tabele, pe baza unei coloane înrudite între ele.
Selecție din tabelul „Orders”:
Selecție din tabelul „Customers”:
Coloana „CustomerID” din tabelul „Orders” se referă la „CustomerID” din tabelul „Customers”. Relația dintre cele două tabele de mai sus este coloana „CustomerID”.
Putem crea următoarea instrucțiune SQL (care conține un INNER JOIN), care selectează înregistrările care au valori potrivite în ambele tabele:
SELECT Orders.OrderID, Customers.CustomerName, Orders.OrderDate
FROM Orders
INNER JOIN Customers ON Orders.CustomerID=Customers.CustomerID;
Diferite tipuri de SQL JOINs
Iată diferitele tipuri de JOINs în SQL:
(INNER) JOIN: returnează înregistrările care au valori potrivite în ambele tabele
LEFT (OUTER) JOIN: returnează toate înregistrările din tabelul din stânga și înregistrările potrivite din tabelul din dreapta
RIGHT (OUTER) JOIN: returnează toate înregistrările din tabelul din dreapta și înregistrările potrivite din tabelul din stânga
FULL (OUTER) JOIN: returnează toate înregistrările atunci când există o potrivire în tabelul din stânga sau din dreapta
SQL INNER JOIN
SQL INNER JOIN
SQL Cuvântul cheie INNER JOIN
Cuvântul cheie INNER JOIN selectează înregistrările care au valori potrivite în ambele tabele.
Sintaxa INNER JOIN
SELECT column_name(s)
FROM table1
INNER JOIN table2
ON table1.column_name = table2.column_name;
Exemplu SQL INNER JOIN
Următoarea instrucțiune SQL selectează toate comenzile cu informații despre client (customer):
SELECT Orders.OrderID, Customers.CustomerName
FROM Orders
INNER JOIN Customers ON Orders.CustomerID = Customers.CustomerID;
Cuvântul cheie INNER JOIN selectează toate rândurile din ambele tabele, atâta timp cât există o potrivire între coloane. Dacă există înregistrări în tabelul „Orders” care nu au potriviri în „Customers”, aceste comenzi nu vor fi afișate!
JOIN Three Tables
Următoarea declarație SQL selectează toate comenzile cu informații despre client și expeditor (customer and shipper):
SELECT Orders.OrderID, Customers.CustomerName, Shippers.ShipperName
FROM ((Orders
INNER JOIN Customers ON Orders.CustomerID = Customers.CustomerID)
INNER JOIN Shippers ON Orders.ShipperID = Shippers.ShipperID);
SQL LEFT JOIN
SQL LEFT JOIN
Cuvântul cheie SQL LEFT JOIN
Cuvântul cheie LEFT JOIN returnează toate înregistrările din tabelul din stânga (table1), si înregistrările potrivite din tabelul din dreapta (table2). Dacă nu există nicio potrivire din partea dreaptă rezultatul este NULL.
LEFT JOIN Syntax
SELECT column_name(s)
FROM table1
LEFT JOIN table2
ON table1.column_name = table2.column_name;
În unele baze de date LEFT JOIN se numește LEFT OUTER JOIN.
Exemplu SQL LEFT JOIN
Următoarea instrucțiune SQL va selecta toți clienții (customers) și orice comenzi (orders) ar putea avea:
SELECT Customers.CustomerName, Orders.OrderID
FROM Customers
LEFT JOIN Orders ON Customers.CustomerID = Orders.CustomerID
ORDER BY Customers.CustomerName;
Cuvântul cheie LEFT JOIN returnează toate înregistrările din tabelul din stânga (Clienți/Customers), chiar dacă nu există potriviri în tabelul din dreapta (Comenzi/Orders).
SQL RIGHT JOIN
SQL RIGHT JOIN
Cuvântul cheie SQL RIGHT JOIN
Cuvântul cheie RIGHT JOIN returnează toate înregistrările din tabelul din dreapta (table2), si înregistrările potrivite din tabelul din stânga (table1). Când nu există nici o potrivire rezultatul este NULL din partea stângă.
RIGHT JOIN Syntax
SELECT column_name(s)
FROM table1
RIGHT JOIN table2
ON table1.column_name = table2.column_name;
În unele baze de date, RIGHT JOIN se numește RIGHT OUTER JOIN.
Exemplu SQL RIGHT JOIN
Următoarea instrucțiune SQL va returna toți angajații și orice comenzi ar fi făcut:
Cuvântul cheie RIGHT JOIN returnează toate înregistrările din tabelul din dreapta (Angajați/Employees), chiar dacă nu există meciuri în tabelul din stânga (Comenzi/Orders).
SQL FULL OUTER JOIN
SQL FULL OUTER JOIN
Cuvântul cheie SQL FULL OUTER JOIN
Cuvântul cheie FULL OUTER JOIN returnează toate înregistrările atunci când există o potrivire în înregistrările tabelului stânga (tabel1) sau dreapta (tabel2).
FULL OUTER JOIN poate returna seturi de rezultate foarte mari!
FULL OUTER JOIN și FULL JOIN sunt aceleași.
FULL OUTER JOIN Syntax
SELECT column_name(s)
FROM table1
FULL OUTER JOIN table2
ON table1.column_name = table2.column_name
WHERE condition;
Exemplu SQL FULL OUTER JOIN
Următoarea instrucțiune SQL selectează toți clienții și toate comenzile:
SELECT Customers.CustomerName, Orders.OrderID
FROM Customers
FULL OUTER JOIN Orders ON Customers.CustomerID=Orders.CustomerID
ORDER BY Customers.CustomerName;
Cuvântul cheie FULL OUTER JOIN returnează toate înregistrările de potrivire din ambele tabele, indiferent dacă celălalt tabel se potrivește sau nu. Așadar, dacă există „rânduri” (rows) în „Clienți” (Customers) care nu au potriviri în „Comenzi” (Orders) sau dacă există „rânduri” (rows) în „Comenzi” (Orders) care nu au potriviri în „Clienți” (Customers), aceste rânduri vor fi listate și ele.
SQL SELF JOIN
SQL Self JOIN
Un Self JOIN este o alăturare obișnuită, dar tabelul este unit cu sine.
Sintaxa Self JOIN
SELECT column_name(s)
FROM table1 T1, table1 T2
WHERE condition;
T1 și T2 sunt aliasuri diferite pentru aceeași tabelă.
Exemplu SQL Self JOIN
Următoarea instrucțiune SQL se potrivește cu clienții (customers) care provin din același oraș:
SELECT A.CustomerName AS CustomerName1, B.CustomerName AS CustomerName2, A.City
FROM Customers A, Customers B
WHERE A.CustomerID <> B.CustomerID
AND A.City = B.City
ORDER BY A.City;
SQL UNION
Operatorul SQL UNION
Operatorul UNION este utilizat pentru a combina setul de rezultate a două sau mai multe declarații SELECT.
Fiecare declarație SELECT din UNION trebuie să aibă același număr de coloane
Coloanele trebuie să aibă, de asemenea, tipuri de date similare
Coloanele din fiecare instrucțiune SELECT trebuie să fie, de asemenea, în aceeași ordine
Sintaxa UNION
SELECT column_name(s) FROM table1
UNION
SELECT column_name(s) FROM table2;
Sintaxa UNION ALL
Operatorul UNION selectează în mod implicit doar valori distincte. Pentru a permite valori duplicate, utilizați UNION ALL:
SELECT column_name(s) FROM table1
UNION ALL
SELECT column_name(s) FROM table2;
Numele coloanelor din setul de rezultate sunt de obicei egale cu numele coloanelor din prima declarație SELECT din UNION.
Exemplu SQL UNION
Următoarea instrucțiune SQL returnează orașele (doar valori distincte) atât din „Clienți” (Customers), cât și din „Furnizori” (Suppliers):
SELECT City FROM Customers
UNION
SELECT City FROM Suppliers
ORDER BY City;
Dacă unii clienți (customers) sau furnizori (suppliers) au același oraș, fiecare oraș va fi listat o singură dată, deoarece UNION selectează doar valori distincte. Utilizați UNION ALL pentru a selecta, de asemenea, valori duplicate!
Exemplu SQL UNION ALL
Următoarea instrucțiune SQL returnează orașele (de asemenea, valori duplicate) atât din tabela „Clienți” (Customers), cât și din „Furnizori” (Suppliers):
SELECT City FROM Customers
UNION ALL
SELECT City FROM Suppliers
ORDER BY City;
SQL UNION cu WHERE
Următoarea instrucțiune SQL returnează orașele germane (doar valori distincte) atât din tabela „Clienți” (Customers), cât și din „Furnizori” (Suppliers):
SELECT City, Country FROM Customers
WHERE Country='Germania'
UNION
SELECT City, Country FROM Suppliers
WHERE Country='Germania'
ORDER BY City;
SQL UNION ALL cu WHERE
Următoarea instrucțiune SQL returnează orașele germane (de asemenea, valori duplicate) atât din tabela „Clienți” (Customers), cât și din „Furnizori” (Suppliers):
SELECT City, Country FROM Customers
WHERE Country='Germania'
UNION ALL
SELECT City, Country FROM Suppliers
WHERE Country='Germania'
ORDER BY City;
Un alt exemplu UNION
Următoarea instrucțiune SQL listează toți clienții (customers) și furnizorii (suppliers):
SELECT 'Customer' As Type, ContactName, City, Country
FROM Customers
UNION
SELECT 'Supplier', ContactName, City, Country
FROM Suppliers;
Observați „AS Type” de mai sus - este un alias. Alias-urile SQL sunt utilizate pentru a da un nume temporar unei tabele sau unei coloane. Un alias există doar pe durata interogării. Așadar, aici am creat o coloană temporară numită „Tip” (Type), care listează dacă persoana de contact este „Client” (Customer) sau „Furnizor” (Supplier).
SQL GROUP BY
SQL GROUP BY
Instrucțiunea SQL GROUP BY
Instrucțiunea GROUP BY grupează rândurile care au aceleași valori în rânduri sumare, cum ar fi „găsiți numărul de clienți din fiecare țară”.
Instrucțiunea GROUP BY este adesea folosită cu funcții agregate (COUNT, MAX, MIN, SUM, AVG) pentru a grupa setul de rezultate cu una sau mai multe coloane.
Sintaxa GROUP BY
SELECT column_name(s)
FROM table_name
WHERE condition
GROUP BY column_name(s)
ORDER BY column_name(s);
Exemple SQL GROUP BY
Următoarea instrucțiune SQL listează numărul de clienți (customers) din fiecare țară:
SELECT COUNT(CustomerID), Country
FROM Customers
GROUP BY Country;
Următoarea instrucțiune SQL listează numărul de clienți (customers) din fiecare țară, sortat de la mare până la mic:
SELECT COUNT(CustomerID), Country
FROM Customers
GROUP BY Country
ORDER BY COUNT(CustomerID) DESC;
Exemplu GROUP BY Cu JOIN
Următoarea instrucțiune SQL listează numărul de comenzi (orders) trimise de fiecare expeditor (shipper):
SELECT Shippers.ShipperName, COUNT(Orders.OrderID) AS NumberOfOrders FROM Orders
LEFT JOIN Shippers ON Orders.ShipperID = Shippers.ShipperID
GROUP BY ShipperName;
SQL HAVING
Clauza SQL HAVING
Clauza HAVING a fost adăugată la SQL, deoarece cuvântul cheie WHERE nu a putut fi utilizat cu funcții de agregare.
Sintaxa HAVING
SELECT column_name(s)
FROM table_name
WHERE condition
GROUP BY column_name(s)
HAVING condition
ORDER BY column_name(s);
Exemple SQL HAVING
Următoarea instrucțiune SQL listează numărul de clienți (customers) din fiecare țară. Includeți numai țările cu mai mult de 5 clienți (customers):
SELECT COUNT(CustomerID), Country
FROM Customers
GROUP BY Country
HAVING COUNT(CustomerID) > 5;
Următoarea instrucțiune SQL listează numărul de clienți (customers) din fiecare țară, sortat de la mare la cel mai mic (include numai țările cu mai mult de 5 clienți (customers)):
SELECT COUNT(CustomerID), Country
FROM Customers
GROUP BY Country
HAVING COUNT(CustomerID) > 5
ORDER BY COUNT(CustomerID) DESC;
Mai multe exemple SQL HAVING
Următoarea instrucțiune SQL listează angajații care au înregistrat mai mult de 10 comenzi (orders):
SELECT Employees.LastName, COUNT(Orders.OrderID) AS NumberOfOrders
FROM (Orders
INNER JOIN Employees ON Orders.EmployeeID = Employees.EmployeeID)
GROUP BY LastName
HAVING COUNT(Orders.OrderID) > 10;
Următoarea declarație SQL listează dacă angajații „Popescu” sau „Ionescu” au înregistrat mai mult de 25 de comenzi (orders):
SELECT Employees.LastName, COUNT(Orders.OrderID) AS NumberOfOrders
FROM Orders
INNER JOIN Employees ON Orders.EmployeeID = Employees.EmployeeID
WHERE LastName = 'Popescu' OR LastName = 'Ionescu'
GROUP BY LastName
HAVING COUNT(Orders.OrderID) > 25;
SQL EXISTS
SQL EXISTS
Operatorul SQL EXISTS
Operatorul EXISTS este utilizat pentru a testa existența oricărei înregistrări într-o subquery.
Operatorul EXISTS returnează adevărat dacă subquery returnează una sau mai multe înregistrări.
Sintaxa EXISTS
SELECT column_name(s)
FROM table_name
WHERE EXISTS
(SELECT column_name FROM table_name WHERE condition);
Exemple SQL EXISTS
Următoarea instrucțiune SQL returnează TRUE și listează furnizorii (suppliers) cu un preț al produsului mai mic de 20:
SELECT SupplierName
FROM Suppliers
WHERE EXISTS (SELECT ProductName FROM Products WHERE Products.SupplierID = Suppliers.supplierID AND Price < 20);
Următoarea instrucțiune SQL returnează TRUE și listează furnizorii (suppliers) cu un preț de produs egal cu 22:
SELECT SupplierName
FROM Suppliers
WHERE EXISTS (SELECT ProductName FROM Products WHERE Products.SupplierID = Suppliers.supplierID AND Price = 22);
SQL ANY și ALL
SQL ANY și ALL
Operatorii SQL ANY și ALL
Operatorii ANY și ALL sunt folosiți cu o clauză WHERE sau HAVING.
Operatorul ANY returnează adevărat dacă oricare dintre valorile subquery îndeplinește condiția.
Operatorul ALL returnează adevărat dacă toate valorile subquery corespund condiției.
Sintaxa ANY
SELECT column_name(s)
FROM table_name
WHERE column_name operator ANY
(SELECT column_name FROM table_name WHERE condition);
Sintaxa ALL
SELECT column_name(s)
FROM table_name
WHERE column_name operator ALL
(SELECT column_name FROM table_name WHERE condition);
Operatorul trebuie să fie un operator de comparație standard (=, <>,! =,>,> =, <, Sau <=);
Exemple SQL ANY
Operatorul ANY returnează TRUE dacă oricare dintre valorile subquery îndeplinește condiția.
Următoarea instrucțiune SQL returnează TRUE și listează numele produsului dacă găsește ANY înregistrări în tabelul OrderDetails unde cantitate=10 (quantity = 10):
SELECT ProductName
FROM Products
WHERE ProductID = ANY (SELECT ProductID FROM OrderDetails WHERE Quantity = 10);
Următoarea instrucțiune SQL returnează TRUE și listează numele produsului dacă găsește ANY înregistrări în tabelul OrderDetails unde cantitate>99 (quantity > 99):
SELECT ProductName
FROM Products
WHERE ProductID = ANY (SELECT ProductID FROM OrderDetails WHERE Quantity > 99);
Exemplu SQL ALL
Operatorul ALL returnează TRUE dacă toate valorile subquery îndeplinesc condiția.
Următoarea instrucțiune SQL returnează TRUE și listează numele produselor dacă înregistrările ALL din tabelul OrderDetails au cantitate=10 (quantity = 10) (deci, acest exemplu va returna FALSE, deoarece nu înregistrările ALL din tabelul OrderDetails au cantitate = 10 (quantity = 10)):
SELECT ProductName
FROM Products
WHERE ProductID = ALL (SELECT ProductID FROM OrderDetails WHERE Quantity = 10);
SQL SELECT INTO
SQL SELECT INTO
Instrucțiunea SQL SELECT INTO
Instrucțiunea SELECT INTO copiază datele dintr-o tabelă într-un nou tabel.
Sintaxa SELECT INTO
Copiați toate coloanele într-un nou tabel:
SELECT *
INTO newtable [IN externaldb]
FROM oldtable
WHERE condition;
Copiați doar câteva coloane într-un nou tabel:
SELECT column1, column2, column3, ...
INTO newtable [IN externaldb]
FROM oldtable
WHERE condition;
Noua tabelă va fi creată cu numele și coloanele definite în tabelul vechi. Puteți crea nume de coloane noi folosind clauza AS.
Exemple SQL SELECT INTO
Următoarea instrucțiune SQL creează o copie de rezervă a Clienților (Customers):
SELECT * INTO CustomersBackup2017
FROM Customers;
Următoarea instrucțiune SQL folosește clauza IN pentru a copia tabela într-un nou tabel într-o altă bază de date:
SELECT * INTO CustomersBackup2017 IN 'Backup.mdb'
FROM Customers;
Următoarea instrucțiune SQL copiază doar câteva coloane într-un nou tabel:
SELECT CustomerName, ContactName INTO CustomersBackup2017
FROM Customers;
Următoarea instrucțiune SQL copiază doar clienții (customers) germani într-un nou tabel:
SELECT * INTO CustomersGermania
FROM Customers
WHERE Country = 'Germania';
Următoarea instrucțiune SQL copiază date din mai multe tabele într-un nou tabel:
SELECT Customers.CustomerName, Orders.OrderID
INTO CustomersOrderBackup2017
FROM Customers
LEFT JOIN Orders ON Customers.CustomerID = Orders.CustomerID;
SELECT INTO poate fi, de asemenea, utilizat pentru a crea un tabel nou, gol, folosind schema altuia. Adaugă doar o clauză WHERE care determină ca interogarea să nu returneze date:
SELECT * INTO newtable
FROM oldtable
WHERE 1 = 0;
SQL INSERT INTO SELECT
SQL INSERT INTO SELECT
Instrucțiunea SQL INSERT INTO SELECT
Instrucțiunea INSERT INTO SELECT copiază datele dintr-un tabel și le introduce într-un alt tabel.
INSERT INTO SELECT necesită ca tipurile de date din sursele și tabelele țintă (target) să se potrivească
Înregistrările existente în tabelul țintă (target) nu sunt afectate
Sintaxa INSERT INTO SELECT
Copiați toate coloanele de la un tabel la altul:
INSERT INTO table2
SELECT * FROM table1
WHERE condition;
Copiați doar câteva coloane dintr-un tabel într-un alt tabel:
INSERT INTO table2 (column1, column2, column3, ...)
SELECT column1, column2, column3, ...
FROM table1
WHERE condition;
Exemple SQL INSERT INTO SELECT
Următoarea instrucțiune SQL copiază „Furnizorii” (Suppliers) în „Clienți” (Customers) (coloanele care nu sunt completate cu date, vor conține NULL):
INSERT INTO Customers (CustomerName, City, Country)
SELECT SupplierName, City, Country FROM Suppliers;
Următoarea instrucțiune SQL copiază „Furnizorii” (Suppliers) în „Clienți” (Customers) (completați toate coloanele):
INSERT INTO Customers (CustomerName, ContactName, Address, City, PostalCode, Country)
SELECT SupplierName, ContactName, Address, City, PostalCode, Country FROM Suppliers;
Următoarea instrucțiune SQL copiază numai furnizorii germani în „Clienți” (Customers):
INSERT INTO Customers (CustomerName, City, Country)
SELECT SupplierName, City, Country FROM Suppliers
WHERE Country='Germania';
SQL CASE
SQL CASE
Instrucțiunea SQL CASE
Instrucțiunea CASE trece prin condiții și returnează o valoare atunci când este îndeplinită prima condiție (ca o instrucțiune IF-THEN-ELSE). Deci, odată ce o condiție este adevărată, aceasta va opri citirea și va returna rezultatul. Dacă condițiile nu sunt adevărate, aceasta returnează valoarea în clauza ELSE.
Dacă nu există nici o parte ELSE și nici o condiție nu este adevărată, se returnează NULL.
Sintaxa CASE
CASE
WHEN condition1 THEN result1
WHEN condition2 THEN result2
WHEN conditionN THEN resultN
ELSE result
END;
Exemple SQL CASE
Următorul SQL trece prin condiții și returnează o valoare atunci când este îndeplinită prima condiție:
SELECT OrderID, Quantity,
CASE
WHEN Quantity > 30 THEN "The quantity is greater than 30"
WHEN Quantity = 30 THEN "The quantity is 30"
ELSE "The quantity is under 30"
END AS QuantityText
FROM OrderDetails;
Următorul SQL va ordona (order) clienții (customers) după oraș. Cu toate acestea, dacă orașul este NULL, atunci ordonați (order) după țară:
SELECT CustomerName, City, Country
FROM Customers
ORDER BY
(CASE
WHEN City IS NULL THEN Country
ELSE City
END);
SQL Funcții NULL
Funcții SQL NULL
Funcții SQL IFNULL(), ISNULL(), COALESCE() și NVL()
Să presupunem că coloana "UnitsOnOrder" este opțională și poate conține valori NULL.
Următoarea declarație SELECT:
SELECT ProductName, UnitPrice * (UnitsInStock + UnitsOnOrder)
FROM Products;
În exemplul de mai sus, dacă oricare dintre valorile "UnitsOnOrder" este NULL, rezultatul va fi NULL.
Soluţii
MySQL
Funcția MySQL IFNULL() vă permite să returnați o valoare alternativă dacă o expresie este NULL:
SELECT ProductName, UnitPrice * (UnitsInStock + IFNULL(UnitsOnOrder, 0))
FROM Products;
sau putem folosi funcția COALESCE(), astfel:
SELECT ProductName, UnitPrice * (UnitsInStock + COALESCE(UnitsOnOrder, 0))
FROM Products;
SQL Server
Funcția SQL ISNULL() vă permite să returnați o valoare alternativă atunci când o expresie este NULL:
SELECT ProductName, UnitPrice * (UnitsInStock + ISNULL(UnitsOnOrder, 0))
FROM Products;
MS Access
Funcția MS Access IsNull() returnează TRUE (-1) dacă expresia este o valoare nulă, altfel returnează FALSE (0):
SELECT ProductName, UnitPrice * (UnitsInStock + IIF(IsNull(UnitsOnOrder), 0, UnitsOnOrder))
FROM Products;
Oracle
Funcția Oracle NVL() obține același rezultat:
SELECT ProductName, UnitPrice * (UnitsInStock + NVL(UnitsOnOrder, 0))
FROM Products;
SQL Proceduri stocate
SQL Stored Procedures
Proceduri stocate SQL pentru SQL Server (SQL Stored Procedures for SQL Server)
Ce este o procedură stocată (Stored Procedure)?
O procedură stocată (Stored Procedure) este un cod SQL pregătit pe care îl puteți salva, astfel încât codul poate fi reutilizat din nou și din nou.
Așadar, dacă aveți o interogare SQL pe care o scrieți de mai multe ori, salvați-o ca o procedură stocată (Stored Procedure) și apoi apelați-o pentru a o executa.
De asemenea, puteți trece parametrii la o procedură stocată (Stored Procedure), astfel încât procedura stocată (Stored Procedure) să poată acționa în funcție de valoarea (valorile) parametrului care este trecută.
Sintaxa de procedură stocată (Stored Procedure)
CREATE PROCEDURE procedure_name
AS
sql_statement
GO;
Execute a Stored Procedure
EXEC procedure_name;
Exemplu de procedură stocată (stored procedure)
Următoarea instrucțiune SQL creează o procedură stocată (stored procedure) numită "SelectAllCustomers" care selectează toate înregistrările din tabelul "Clienți" (Customers):
CREATE PROCEDURE SelectAllCustomers
AS
SELECT * FROM Customers
GO;
Executați procedura stocată (stored procedure) de mai sus după cum urmează:
EXEC SelectAllCustomers;
Procedura stocată cu un singur parametru
Următoarea instrucțiune SQL creează o procedură stocată (stored procedure) care selectează Clienții (Customers) dintr-un anumit oraș (City) din tabelul „Clienți” (Customers):
CREATE PROCEDURE SelectAllCustomers @City nvarchar(30)
AS
SELECT * FROM Customers WHERE City = @City
GO;
Executați procedură stocată (stored procedure) mai sus după cum urmează:
EXEC SelectAllCustomers @City = "Londra";
Procedură stocată cu mai mulți parametri
Configurarea mai multor parametri este foarte ușoară. Trebuie doar să enumerați fiecare parametru și tipul de date separat printr-o virgulă, așa cum se arată mai jos.
Următoarea instrucțiune SQL creează o procedură stocată (stored procedure) care selectează clienții (Customers) dintr-un anumit oraș (City) cu un anumit cod poștal (PostalCode) din tabelul „Clienți” (Customers):
CREATE PROCEDURE SelectAllCustomers @City nvarchar(30), @PostalCode nvarchar(10)
AS
SELECT * FROM Customers WHERE City = @City AND PostalCode = @PostalCode
GO;
Executați procedura stocată (stored procedure) mai sus după cum urmează:
EXEC SelectAllCustomers @City = "Londra", @PostalCode = "WA1 1DP";
SQL Comentarii
Comentarii SQL
Comentariile sunt utilizate pentru a explica secțiunile instrucțiunilor SQL sau pentru a preveni executarea de instrucțiuni SQL.
Exemplele din acest capitol nu vor funcționa în Firefox și Microsoft Edge!
Comentariile nu sunt acceptate în bazele de date Microsoft Access. Firefox și Microsoft Edge folosesc baza de date Microsoft Access în exemplele noastre.
Comentarii cu o singură linie
Comentariile cu o singură linie încep cu -.
Orice text între - și sfârșitul liniei va fi ignorat (nu va fi executat).
Următorul exemplu utilizează un comentariu cu o singură linie ca explicație:
--Select all:
SELECT * FROM Customers;
Următorul exemplu utilizează un comentariu cu o singură linie pentru a ignora sfârșitul unei linii:
SELECT * FROM Customers -- WHERE City='Berlin';
Următorul exemplu utilizează un comentariu cu o singură linie pentru a ignora o afirmație:
--SELECT * FROM Customers;
SELECT * FROM Products;
Comentarii cu mai multe linii
Comentariile cu mai multe linii încep cu / * și se termină cu * /.
Orice text între / * și * / va fi ignorat.
Următorul exemplu utilizează un comentariu cu mai multe linii ca explicație:
/*Selectați toate coloanele
din toate înregistrările
în tabelul Clienți (Customers): * /
SELECT * FROM Customers;
Următorul exemplu utilizează un comentariu cu mai multe linii pentru a ignora multe afirmații:
/*SELECT * FROM Customers;
SELECT * FROM Products;
SELECT * FROM Orders;
SELECT * FROM Categories;*/
SELECT * FROM Suppliers;
Pentru a ignora doar o parte dintr-o afirmație, utilizați și / * * / comentariu.
Următorul exemplu utilizează un comentariu pentru a ignora o parte a unei linii:
SELECT CustomerName, /*City,*/ Country FROM Customers;
Următorul exemplu utilizează un comentariu pentru a ignora o parte dintr-o afirmație:
SELECT * FROM Customers WHERE (CustomerName LIKE 'L%'
OR CustomerName LIKE 'R%' /*OR CustomerName LIKE 'S%'
OR CustomerName LIKE 'T%'*/ OR CustomerName LIKE 'W%')
AND Country='USA'
ORDER BY CustomerName;
SQL CREATE DATABASE
SQL CREATE DATABASE
Instrucțiunea SQL CREATE DATABASE
Instrucțiunea CREATE DATABASE este utilizată pentru a crea o nouă bază de date SQL.
Sintaxă
CREATE DATABASE databasename;
CREATE DATABASE Example
Următoarea instrucțiune SQL creează o bază de date numită "testDB":
CREATE DATABASE testDB;
Asigurați-vă că aveți privilegiul admin înainte de a crea orice bază de date. Odată creată o bază de date, o puteți verifica în lista bazelor de date cu următoarea comandă SQL: SHOW DATABASES;
SQL DROP DATABASE
SQL DROP DATABASE
Instrucțiunea SQL DROP DATABASE
Instrucțiunea DROP DATABASE este utilizată pentru a renunța la o bază de date SQL existentă.
Sintaxă
DROP DATABASE databasename;
Aveți grijă înainte de a renunța la o bază de date. Ștergerea unei baze de date va duce la pierderea informațiilor complete stocate în baza de date!
Exemplu DROP DATABASE
Următoarea instrucțiune SQL renunță la baza de date existentă "testDB":
DROP DATABASE testDB;
Asigurați-vă că aveți privilegiul admin înainte de a renunța la orice bază de date. Odată ce o bază de date este abandonată, o puteți verifica în lista bazelor de date cu următoarea comandă SQL: SHOW DATABASES;
SQL BACKUP DATABASE
SQL BACKUP DATABASE
SQL BACKUP DATABASE pentru SQL Server
Instrucțiunea SQL BACKUP DATABASE
Instrucțiunea BACKUP DATABASE este utilizată în SQL Server pentru a crea o copie de rezervă completă a unei baze de date SQL existente.
Sintaxă
BACKUP DATABASE databasename
TO DISK = 'filepath';
Instrucțiunea SQL BACKUP WITH DIFFERENTIAL
O copie de rezervă diferențială (differential back up) face doar backup pentru părțile bazei de date care s-au modificat de la ultima copie de rezervă completă a bazei de date.
Sintaxă
BACKUP DATABASE databasename
TO DISK = 'filepath'
WITH DIFFERENTIAL;
Exemplu BACKUP DATABASE
Următoarea instrucțiune SQL creează o copie de rezervă completă (full back up) a bazei de date existente "testDB" pe discul D:
BACKUP DATABASE testDB
TO DISK = 'D:\backups\testDB.bak';
Faceți întotdeauna o copie de siguranță (back up) a bazei de date pe o unitate diferită de baza de date reală. Apoi, dacă primiți un crash pe disc, nu veți pierde fișierul dvs. de rezervă împreună cu baza de date.
Exemplu BACKUP WITH DIFFERENTIAL
Următoarea instrucțiune SQL creează o copie de rezervă diferențială (differential back up) a bazei de date "testDB":
BACKUP DATABASE testDB
TO DISK = 'D:\backups\testDB.bak'
WITH DIFFERENTIAL;
SQL CREATE TABLE
SQL CREATE TABLE
Instrucțiunea SQL CREATE TABLE
Instrucțiunea CREATE TABLE este utilizată pentru a crea o nouă tabelă într-o bază de date.
Sintaxă
CREATE TABLE table_name (
column1 datatype,
column2 datatype,
column3 datatype,
....
);
Parametrii coloanelor specifică numele coloanelor tabelului.
Parametrul datatype specifică tipul de date pe care le poate deține coloana (de exemplu, varchar, integer, date, etc.).
Exemplu SQL CREATE TABLE
Următorul exemplu creează un tabel numit „Persoane” (Persons) care conține cinci coloane: PersonID, LastName, FirstName, Address și City:
CREATE TABLE Persons (
PersonID int,
LastName varchar(255),
FirstName varchar(255),
Address varchar(255),
City varchar(255)
);
Coloana PersonID este de tip int și va deține un numar intreg (integer).
Coloanele LastName, FirstName, Address și City sunt de tip varchar și vor conține caractere (characters), iar lungimea maximă pentru aceste câmpuri este de 255 de caractere.
Tabelul gol „Persoane” (Persons) poate fi completat acum cu date cu instrucțiunea SQL INSERT INTO.
Creați o tabelă folosind o altă tabelă
O copie a unui tabel existent poate fi, de asemenea, creată folosind CREATE TABLE.
Noul tabel primește aceleași definiții ale coloanei. Toate coloanele sau coloanele specifice pot fi selectate.
Dacă creați o nouă tabelă folosind o tabelă existentă, noua tabelă va fi completată cu valorile existente din tabelul vechi.
Sintaxă
CREATE TABLE new_table_name AS
SELECT column1, column2,...
FROM existing_table_name
WHERE ....;
Următorul SQL creează un nou tabel numit "TestTables" (care este o copie a tabelului "Clienți" (Customers)):
CREATE TABLE TestTable AS
SELECT customername, contactname
FROM customers;
SQL DROP TABLE
SQL DROP TABLE
Instrucțiunea SQL DROP TABLE
Instrucțiunea DROP TABLE este utilizată pentru a renunța la un tabel existent într-o bază de date.
Sintaxă
DROP TABLE table_name;
Aveți grijă înainte de a arunca o masă. Ștergerea unui tabel va duce la pierderea informațiilor complete stocate în tabel!
Exemplu DROP TABLE
Următoarea instrucțiune SQL renunță la tabelul existent "Expeditori" (Shippers):
DROP TABLE Shippers;
SQL TRUNCATE TABLE
Instrucțiunea TRUNCATE TABLE este utilizată pentru a șterge datele dintr-un tabel, dar nu și tabelul în sine.
Sintaxă
TRUNCATE TABLE table_name;
SQL ALTER TABLE
SQL ALTER TABLE
Instrucțiunea SQL ALTER TABLE
Instrucțiunea ALTER TABLE este utilizată pentru a adăuga, șterge sau modifica coloane dintr-un tabel existent.
Instrucțiunea ALTER TABLE este de asemenea folosită pentru a adăuga și a scădea diverse constrângeri pe un tabel existent.
ALTER TABLE - ADD Column
Pentru a adăuga o coloană într-un tabel, utilizați următoarea sintaxă:
ALTER TABLE table_name
ADD column_name datatype;
Următorul SQL adaugă o coloană „Email” la tabelul „Clienți” (Customers):
ALTER TABLE Customers
ADD Email varchar(255);
ALTER TABLE - DROP COLUMN
Pentru a șterge o coloană dintr-un tabel, utilizați următoarea sintaxă (observați că unele sisteme de baze de date nu permit ștergerea unei coloane):
ALTER TABLE table_name
DROP COLUMN column_name;
Următorul SQL șterge coloana „Email” din tabelul „Clienți” (Customers):
ALTER TABLE Customers
DROP COLUMN Email;
ALTER TABLE - ALTER/MODIFY COLUMN
Pentru a modifica tipul de date al unei coloane dintr-un tabel, utilizați următoarea sintaxă:
SQL Server / MS Access:
ALTER TABLE table_name
ALTER COLUMN column_name datatype;
My SQL / Oracle (versiunea anterioară 10G):
ALTER TABLE table_name
MODIFY COLUMN column_name datatype;
Oracle 10G și mai târziu:
ALTER TABLE table_name
MODIFY column_name datatype;
Exemplu SQL ALTER TABLE
Creați tabelul „Persoane” (Persons):
Acum vrem să adăugăm o coloană numită "DateOfBirth" în tabelul "Persoane"(Persons).
Folosim următoarea instrucțiune SQL:
ALTER TABLE Persons
ADD DateOfBirth date;
Observați că noua coloană, "DateOfBirth", este de tip date (data type) și va păstra o dată. Data type specifică ce tip de date poate conține coloana.
Exemplu Modificați Data Type
Acum dorim să schimbăm tipul de date (Data Type) al coloanei numită „DateOfBirth” din tabelul „Persoane”(Persons).
Folosim următoarea instrucțiune SQL:
ALTER TABLE Persons
ALTER COLUMN DateOfBirth year;
Observați că coloana „DateOfBirth” are acum un tip year și va păstra year într-un format de două sau patru cifre.
Exemplu DROP COLUMN
În continuare, dorim să ștergem coloana numită „DateOfBirth” din tabelul „Persoane”(Persons).
Folosim următoarea instrucțiune SQL:
ALTER TABLE Persons
DROP COLUMN DateOfBirth;
SQL Restricții
SQL Constraints
Limitările SQL
Restricțiile SQL sunt utilizate pentru a specifica regulile pentru datele dintr-un tabel.
SQL Creare constrângeri
Constrângerile pot fi specificate atunci când tabela este creată cu instrucțiunea CREATE TABLE sau după crearea tabelului cu instrucțiunea ALTER TABLE.
Sintaxă
CREATE TABLE table_name (
column1 datatype constraint,
column2 datatype constraint,
column3 datatype constraint,
....
);
Limitările SQL
Restricțiile SQL sunt utilizate pentru a specifica regulile pentru datele dintr-un tabel.
Constrângerile sunt utilizate pentru a limita tipul de date care poate intra într-un tabel. Aceasta asigură precizia și fiabilitatea datelor din tabel. Dacă există o încălcare între constrângere și acțiunea de date, acțiunea este anulată.
Constrângerile pot fi la nivel de coloană sau de tabel. Restricțiile de nivel de coloană se aplică unei coloane și restricțiile de nivel de tabel se aplică întregii tabele.
Următoarele constrângeri sunt utilizate în mod obișnuit în SQL:
NOT NULL - Se asigură că o coloană nu poate avea o valoare NULL
UNIQUE - Se asigură că toate valorile dintr-o coloană sunt diferite
PRIMARY KEY - O combinație între NOT NULL ȘI UNIQUE. Identifică în mod unic fiecare rând dintr-un tabel
FOREIGN KEY - Identifică un rând / o înregistrare într-un alt tabel
CHECK - Se asigură că toate valorile dintr-o coloană îndeplinesc o condiție specifică
DEFAULT - Setează o valoare implicită pentru o coloană atunci când nu este specificată nicio valoare
INDEX - Folosit pentru a crea și recupera rapid datele din baza de date
SQL NOT NULL
SQL NOT NULL
SQL Constrângere NOT NULL (SQL NOT NULL Constraint)
În mod implicit, o coloană poate conține valori NULL.
Constrângerea NOT NULL impune o coloană pentru a NU (NOT) accepta valorile NULL.
Acest lucru impune un câmp care să conțină întotdeauna o valoare, ceea ce înseamnă că nu puteți introduce o înregistrare nouă sau să actualizați o înregistrare fără a adăuga o valoare la acest câmp.
SQL NOT NULL în CREATE TABLE
Următorul SQL asigură că coloanele „ID”, „LastName” și „FirstName” NU (NOT) vor accepta valori NULL atunci când se creează tabelul „Persoane” (Persons):
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255) NOT NULL,
Age int
);
SQL NOT NULL în ALTER TABLE
Pentru a crea o restricție NOT NULL pe coloana „Vârstă” (Age) când tabelul „Persoane” (Persons) este deja creat, utilizați următorul SQL:
ALTER TABLE Persons
MODIFY Age int NOT NULL;
SQL UNIQUE
SQL Constrângere UNIQUE (SQL UNIQUE Constraint)
Constrângerea UNIQUE asigură că toate valorile dintr-o coloană sunt diferite.
Atât constrângerile UNIQUE, cât și cele PRIMARY KEY oferă o garanție de unicitate pentru o coloană sau un set de coloane.
O constrângere PRIMARY KEY are automat o restricție UNIQUE.
Cu toate acestea, puteți avea multe constrângeri UNIQUE pe tabelă, dar o singură restricție PRIMARY KEY pe tabelă.
SQL UNIQUE Constraint on CREATE TABLE
Următorul SQL creează o restricție UNIQUE în coloana „ID” atunci când este creată tabela „Persoane” (Persons):
SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL UNIQUE,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int
);
MySQL:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
UNIQUE (ID)
);
Pentru a denumi o constrângere UNIQUE și pentru a defini o restricție UNIQUE pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
CONSTRAINT UC_Person UNIQUE (ID,LastName)
);
SQL UNIQUE Constraint on ALTER TABLE
Pentru a crea o restricție UNIQUE în coloana „ID” atunci când tabelul este deja creat, utilizați următorul SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD UNIQUE (ID);
Pentru a denumi o constrângere UNIQUE și pentru a defini o restricție UNIQUE pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD CONSTRAINT UC_Person UNIQUE (ID,LastName);
DROP a UNIQUE Constraint
Pentru a elimina o restricție UNIQUE, utilizați următorul SQL:
MySQL:
ALTER TABLE Persons
DROP INDEX UC_Person;
SQL Server / Oracle / MS Access:
ALTER TABLE Persons
DROP CONSTRAINT UC_Person;
SQL PRIMARY KEY
SQL PRIMARY KEY
SQL Limitarea PRIMARY KEY (SQL PRIMARY KEY Constraint)
Limitarea PRIMARY KEY (PRIMARY KEY Constraint) identifică în mod unic fiecare înregistrare dintr-un tabel.
Primary keys trebuie să conțină valori UNIQUE și nu pot conține valori NULL.
Un tabel poate avea doar O (ONE) cheie primară (primary key); iar în tabel, această cheie primară (primary key) poate consta din coloane simple sau multiple (câmpuri).
SQL PRIMARY KEY în CREATE TABLE
Următorul SQL creează o PRIMARY KEY în coloana „ID” când se creează tabelul „Persoane” (Persons):
MySQL:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
PRIMARY KEY (ID)
);
SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL PRIMARY KEY,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int
);
Pentru a permite denumirea unei restricții PRIMARY KEY și pentru a defini o restricție PRIMARY KEY pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
CONSTRAINT PK_Person PRIMARY KEY (ID,LastName)
);
În exemplul de mai sus, există doar ONE PRIMARY KEY (PK_Person). Cu toate acestea, VALUE (valoarea) cheii primare (primary key) este alcătuită din TWO COLUMNS (ID + LastName).
SQL PRIMARY KEY în ALTER TABLE
Pentru a crea o restricție PRIMARY KEY în coloana „ID” atunci când tabelul este deja creat, utilizați următorul SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD PRIMARY KEY (ID);
Pentru a permite denumirea unei restricții PRIMARY KEY și pentru a defini o restricție PRIMARY KEY pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD CONSTRAINT PK_Person PRIMARY KEY (ID,LastName);
Dacă utilizați instrucțiunea ALTER TABLE pentru a adăuga o cheie primară (primary key), coloana cheii primare (primary key) trebuie să fi fost deja declarată că nu conține valori NULL (când a fost creat tabelul pentru prima dată).
Renunțare la o restricție PRIMAR KEY (DROP a PRIMARY KEY Constraint)
Pentru a renunța la o restricție PRIMAR KEY, utilizați următorul SQL:
MySQL:
ALTER TABLE Persons
DROP PRIMARY KEY;
SQL Server / Oracle / MS Access:
ALTER TABLE Persons
DROP CONSTRAINT PK_Person;
SQL FOREIGN KEY
SQL FOREIGN KEY
SQL Constrângere FOREIGN KEY (SQL FOREIGN KEY Constraint)
O FOREIGN KEY este o cheie folosită pentru a lega două tabele între ele.
O FOREIGN KEY este un câmp (sau o colecție de câmpuri) dintr-un tabel care se referă la FOREIGN KEY dintr-un alt tabel.
Tabelul care conține cheia străină (foreign key) se numește tabel copil (child table), iar tabelul care conține cheia candidat (candidate key) este denumit referință sau tabel părinte (parent table).
Creați două tabele:
Tabelul „Persoane” (Persons):
Tabelul „Comenzi” (Orders):
Observați că coloana „PersonID” din tabelul „Comenzi” (Orders) indică coloana „PersonID” din tabelul „Persoane” (Persons).
Coloana „PersonID” din tabelul „Persoane” (Persons) este PRIMARY KEY din tabelul „Persoane” (Persons).
Coloana „PersonID” din tabelul „Comenzi” (Orders) este o FOREIGN KEY din tabelul „Comenzi” (Orders).
Limitarea FOREIGN KEY este utilizată pentru a preveni acțiunile care ar distruge legăturile dintre tabele.
Restrângerea FOREIGN KEY împiedică, de asemenea, introducerea datelor nevalide în coloana de cheie străină (foreign key), deoarece aceasta trebuie să fie una dintre valori.
SQL FOREIGN KEY în CREATE TABLE
Următorul SQL creează un FOREIGN KEY în coloana „PersonID” atunci când se creează tabelul „Comenzi” (Orders):
MySQL:
CREATE TABLE Orders (
OrderID int NOT NULL,
OrderNumber int NOT NULL,
PersonID int,
PRIMARY KEY (OrderID),
FOREIGN KEY (PersonID) REFERENCES Persons(PersonID)
);
SQL Server / Oracle / MS Access:
CREATE TABLE Orders (
OrderID int NOT NULL PRIMARY KEY,
OrderNumber int NOT NULL,
PersonID int FOREIGN KEY REFERENCES Persons(PersonID)
);
Pentru a permite denumirea unei restricții FOREIGN KEY și pentru a defini o restricție FOREIGN KEY pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
CREATE TABLE Orders (
OrderID int NOT NULL,
OrderNumber int NOT NULL,
PersonID int,
PRIMARY KEY (OrderID),
CONSTRAINT FK_PersonOrder FOREIGN KEY (PersonID)
REFERENCES Persons(PersonID)
);
SQL FOREIGN KEY în ALTER TABLE
Pentru a crea o restricție FOREIGN KEY în coloana „PersonID” atunci când tabelul „Comenzi” (Orders) este deja creat, utilizați următorul SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Orders
ADD FOREIGN KEY (PersonID) REFERENCES Persons(PersonID);
Pentru a permite denumirea unei constrângeri FOREIGN KEY și pentru a defini o restricție FOREIGN KEY pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Orders
ADD CONSTRAINT FK_PersonOrder
FOREIGN KEY (PersonID) REFERENCES Persons(PersonID);
Eliminare restricție FOREIGN KEY (DROP a FOREIGN KEY Constraint)
Pentru a elimina o restricție FOREIGN KEY, utilizați următorul SQL:
MySQL:
ALTER TABLE Orders
DROP FOREIGN KEY FK_PersonOrder;
SQL Server / Oracle / MS Access:
ALTER TABLE Orders
DROP CONSTRAINT FK_PersonOrder;
SQL CHECK
SQL CHECK
SQL restricție CHECK (SQL CHECK Constraint)
Restrângerea CHECK este utilizată pentru a limita intervalul de valori care poate fi plasat într-o coloană.
Dacă definiți o restricție CHECK pe o singură coloană, aceasta permite doar anumite valori pentru această coloană.
Dacă definiți o restricție CHECK pe o tabelă, aceasta poate limita valorile din anumite coloane pe baza valorilor din alte coloane din rând.
SQL CHECK în CREATE TABLE
Următorul SQL creează o restricție CHECK în coloana „Vârstă” (Age) când se creează tabelul „Persoane” (Persons). Restrângerea CHECK vă asigură că nu puteți avea nicio persoană sub 18 ani:
MySQL:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
CHECK (Age>=18)
);
SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int CHECK (Age>=18)
);
Pentru a permite denumirea unei constrângeri CHECK și pentru a defini o restricție CHECK pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
City varchar(255),
CONSTRAINT CHK_Person CHECK (Age>=18 AND City='Sandnes')
);
SQL CHECK în ALTER TABLE
Pentru a crea o restricție CHECK în coloana „Vârstă” (Age) când tabelul este deja creat, utilizați următorul SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD CHECK (Age>=18);
Pentru a permite denumirea unei constrângeri CHECK și pentru a defini o restricție CHECK pe mai multe coloane, utilizați următoarea sintaxă SQL:
MySQL / SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ADD CONSTRAINT CHK_PersonAge CHECK (Age>=18 AND City='Sandnes');
Eliminare constrângere CHECK (DROP a CHECK Constraint)
Pentru a elimina o constrângere CHECK, utilizați următorul SQL:
SQL Server / Oracle / MS Access:
ALTER TABLE Persons
DROP CONSTRAINT CHK_PersonAge;
MySQL:
ALTER TABLE Persons
DROP CHECK CHK_PersonAge;
SQL DEFAULT
SQL DEFAULT
SQL Restrângerea DEFAULT (SQL DEFAULT Constraint)
Restrângerea DEFAULT este utilizată pentru a furniza o valoare implicită pentru o coloană.
Valoarea implicită va fi adăugată la toate înregistrările noi, dacă nu este specificată nicio altă valoare.
SQL DEFAULT în CREATE TABLE
Următorul SQL stabilește o valoare DEFAULT pentru coloana „Oraș” (City) atunci când se creează tabelul „Persoane” (Persons):
SQL / SQL Server / Oracle / MS Access:
CREATE TABLE Persons (
ID int NOT NULL,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
City varchar(255) DEFAULT 'Sandnes'
);
Restrângerea DEFAULT poate fi de asemenea folosită pentru a insera valori system, utilizând funcții precum GETDATE ():
CREATE TABLE Orders (
ID int NOT NULL,
OrderNumber int NOT NULL,
OrderDate date DEFAULT GETDATE()
);
SQL DEFAULT în ALTER TABLE
Pentru a crea o restricție DEFAULT pe coloana „Oraș” (City) atunci când tabelul este deja creat, utilizați următorul SQL:
MySQL:
ALTER TABLE Persons
ALTER City SET DEFAULT 'Sandnes';
SQL Server:
ALTER TABLE Persons
ADD CONSTRAINT df_City
DEFAULT 'Sandnes' FOR City;
MS Access:
ALTER TABLE Persons
ALTER COLUMN City SET DEFAULT 'Sandnes';
Oracle:
ALTER TABLE Persons
MODIFY City DEFAULT 'Sandnes';
Eliminare constrângere DEFAULT (DROP a DEFAULT Constraint)
Pentru a elimina o constrângere DEFAULT, utilizați următorul SQL:
MySQL:
ALTER TABLE Persons
ALTER City DROP DEFAULT;
SQL Server / Oracle / MS Access:
ALTER TABLE Persons
ALTER COLUMN City DROP DEFAULT;
SQL CREATE INDEX
SQL CREATE INDEX
Instrucțiunea SQL CREATE INDEX
Instrucțiunea CREATE INDEX este utilizată pentru a crea indexuri în tabele.
Se folosesc indexuri pentru a prelua date din baza de date mai rapid decât in caz contrar. Utilizatorii nu pot vedea indexurile, ci sunt folosite doar pentru a accelera căutările / interogările (searches/queries).
Actualizarea unei tabele cu indexuri necesită mai mult timp decât actualizarea unui tabel fără indexuri (deoarece indexurile au nevoie și de o actualizare). Deci, creați doar indexuri pe coloane care vor fi căutate frecvent.
Sintaxă CREATE INDEX
Creează un index într-un tabel. Valorile duplicate sunt permise:
CREATE INDEX index_name
ON table_name (column1, column2, ...);
Sintaxă CREATE UNIQUE INDEX
Creează un index unic pe un tabel. Valorile duplicate nu sunt permise:
CREATE UNIQUE INDEX index_name
ON table_name (column1, column2, ...);
Sintaxa pentru crearea indexurilor variază printre diferite baze de date. Prin urmare: verificați sintaxa pentru a crea indexuri în baza de date.
Exemplu CREATE INDEX
Instrucțiunea SQL de mai jos creează un index numit "idx_lastname" în coloana "LastName" din tabelul "Persoane" (Persons):
CREATE INDEX idx_lastname
ON Persons (LastName);
Dacă doriți să creați un index pe o combinație de coloane, puteți lista numele coloanelor din paranteze, separate prin virgule:
CREATE INDEX idx_pname
ON Persons (LastName, FirstName);
Declarație DROP INDEX (DROP INDEX Statement)
Instrucțiunea DROP INDEX este utilizată pentru a șterge un index dintr-un tabel.
MS Access:
DROP INDEX index_name ON table_name;
SQL Server:
DROP INDEX table_name.index_name;
DB2/Oracle:
DROP INDEX index_name;
MySQL:
ALTER TABLE table_name
DROP INDEX index_name;
SQL AUTO INCREMENT
SQL Câmpul AUTO INCREMENT
Câmpul AUTO INCREMENT
Auto-increment permite un număr unic de generat automat atunci când o nouă înregistrare este introdusă într-un tabel.
Adesea, acesta este câmpul cheie principal (primary key field) pe care am dori să fie creat automat de fiecare dată când se introduce o nouă înregistrare.
Sintaxa pentru MySQL
Următoarea instrucțiune SQL definește coloana "Personid" pentru a fi un câmp cheie primară (primary key field) cu auto-increment din tabelul "Persoane" (Persons):
CREATE TABLE Persons (
Personid int NOT NULL AUTO_INCREMENT,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int,
PRIMARY KEY (Personid)
);
MySQL folosește cuvântul cheie (keyword) AUTO_INCREMENT pentru a efectua o funcție auto-increment.
În mod implicit, valoarea de pornire pentru AUTO_INCREMENT este 1 și va crește cu 1 pentru fiecare înregistrare nouă.
Pentru a permite ca secvența AUTO_INCREMENT să înceapă cu o altă valoare, utilizați următoarea instrucțiune SQL:
ALTER TABLE Persons AUTO_INCREMENT=100;
Pentru a insera o înregistrare nouă în tabelul „Persoane” (Persons), NU (NOT) va trebui să specificăm o valoare pentru coloana „Personid” (o valoare unică va fi adăugată automat):
INSERT INTO Persons (FirstName,LastName)
VALUES ('Ion','Popescu');
Declarația SQL de mai sus ar insera o nouă înregistrare în tabelul „Persoane”(Persons). Coloanei „Personid” i se va atribui o valoare unică. Coloana „FirstName” ar fi setată la „Ion”, iar coloana „LastName” ar fi setată la „Popescu”.
Sintaxa pentru SQL Server
Următoarea instrucțiune SQL definește coloana "Personid" pentru a fi un câmp cheie primară (primary key field) cu auto-increment in tabelul "Persoane" (Persons):
CREATE TABLE Persons (
Personid int IDENTITY(1,1) PRIMARY KEY,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int
);
MS SQL Server folosește cuvântul cheie (primary key) IDENTITY pentru a efectua o funcție de auto-increment (auto-increment feature).
În exemplul de mai sus, valoarea de pornire pentru IDENTITY este 1 și va crește cu 1 pentru fiecare înregistrare nouă.
Pentru a specifica că coloana „Personid” ar trebui să înceapă la valoarea 10 și să crească cu 5, schimbați-o în IDENTITY(10,5)
Pentru a insera o înregistrare nouă în tabelul „Persoane” (Persons), NU (NOT) va trebui să specificăm o valoare pentru coloana „Personid” (o valoare unică va fi adăugată automat):
INSERT INTO Persons (FirstName,LastName)
VALUES ('Ion','Popecu');
Declarația SQL de mai sus ar insera o nouă înregistrare în tabelul „Persoane” (Persons). Coloanei „Personid” i se va atribui o valoare unică. Coloana „FirstName” ar fi setată la „Ion”, iar coloana „LastName” ar fi setată la „Popescu”.
Sintaxa pentru Access
Următoarea instrucțiune SQL definește coloana "Personid" pentru a fi un câmp cheie primară cu auto-increment (auto-increment primary key field) în tabelul "Persoane" (Persons):
CREATE TABLE Persons (
Personid AUTOINCREMENT PRIMARY KEY,
LastName varchar(255) NOT NULL,
FirstName varchar(255),
Age int
);
MS Access utilizează cuvântul cheie (keyword) AUTOINCREMENT pentru a efectua o funcție auto-increment (auto-increment feature).
În mod implicit, valoarea de pornire pentru AUTOINCREMENT este 1 și va crește cu 1 pentru fiecare înregistrare nouă.
Pentru a specifica că coloana „Personid” ar trebui să înceapă la valoarea 10 și să crească cu 5, schimbați autoincrementul în AUTOINCREMENT(10,5).
Pentru a insera o înregistrare nouă în tabelul „Persoane” (Persons), NU (NOT) va trebui să specificăm o valoare pentru coloana „Personid” (o valoare unică va fi adăugată automat):
INSERT INTO Persons (FirstName,LastName)
VALUES ('Ion','Popescu');
Declarația SQL de mai sus ar insera o nouă înregistrare în tabelul „Persoane”(Persons). Coloanei „Personid” i se va atribui o valoare unică. Coloana „FirstName” ar fi setată la „Ion”, iar coloana „LastName” ar fi setată la „Popescu”.
Sintaxa pentru Oracle
În Oracle codul este puțin mai complicat.
Va trebui să creați un câmp cu auto-increment (auto-increment field) cu obiectul secvenței (sequence object) (acest obiect generează o secvență numerică).
Utilizați următoarea sintaxă CREATE SEQUENCE:
CREATE SEQUENCE seq_person
MINVALUE 1
START WITH 1
INCREMENT BY 1
CACHE 10;
Codul de mai sus creează un obiect de secvență (sequence object) numit seq_person, care începe cu 1 și va crește cu 1. De asemenea, va stoca (cache) până la 10 valori pentru performanță. Opțiunea cache specifică câte valori de secvență (sequence values) vor fi stocate în memorie pentru acces mai rapid.
Pentru a introduce o nouă înregistrare în tabelul „Persoane” (Persons), va trebui să folosim funcția nextval (această funcție preia următoarea valoare din secvența seq_person):
INSERT INTO Persons (Personid,FirstName,LastName)
VALUES (seq_person.nextval,'Ion','Popescu');
Declarația SQL de mai sus ar insera o nouă înregistrare în tabelul „Persoane” (Persons). Coloana „Personid” avea să i se atribuie următorul număr din secvența seq_person. Coloana „FirstName” ar fi setată la „Ion”, iar coloana „LastName” ar fi setată la „Popescu”.
SQL Date
SQL Lucrând cu datele
Datele SQL
Partea cea mai dificilă atunci când lucrați cu datele este să vă asigurați că formatul datei pe care încercați să îl inserați se potrivește cu formatul coloanei de date din baza de date.
Atâta timp cât datele dvs. conțin doar porțiunea de date (date portion), întrebările dvs. vor funcționa așa cum vă așteptați. Cu toate acestea, dacă este implicată o porție de timp (time portion), devine mai complicat.
SQL Date Data Types
MySQL vine cu următoarele tipuri de date pentru stocarea date/time în baza de date:
DATE - format YYYY-MM-DD
DATETIME - format: YYYY-MM-DD HH:MI:SS
TIMESTAMP - format: YYYY-MM-DD HH:MI:SS
YEAR - format YYYY or YY
SQL Server vine cu următoarele tipuri de date pentru stocarea date/time în baza de date:
DATE - format YYYY-MM-DD
DATETIME - format: YYYY-MM-DD HH:MI:SS
SMALLDATETIME - format: YYYY-MM-DD HH:MI:SS
TIMESTAMP - format: a unique number (un număr unic)
Tipurile de date (date types) sunt alese pentru o coloană atunci când creați un nou tabel în baza de date!
SQL Lucrul cu date
Puteți compara ușor două date dacă nu este implicată o componentă de timp!
Presupunem că avem tabelul „Comenzi” (Orders):
Acum dorim să selectăm înregistrările cu OrderDate "2008-11-11" din tabel.
Folosim următoarea declarație SELECT:
SELECT * FROM Orders WHERE OrderDate='2008-11-11'
Dacă folosim aceeași declarație SELECT ca mai sus:
SELECT * FROM Orders WHERE OrderDate='2008-11-11'
nu vom obține niciun rezultat! Acest lucru se datorează faptului că interogarea caută doar date fără o porție de timp (time portion).
Pentru a vă menține întrebările simple și ușor de întreținut, nu permiteți componentele timpului în datele dvs.!
SQL Vizualizări
Vizualizări SQL (SQL Views)
Instrucțiunea SQL CREATE VIEW
În SQL, o vizualizare (view) este un tabel virtual bazat pe setul de rezultate al unei instrucțiuni SQL.
O vizualizare (view) conține rânduri și coloane, la fel ca un tabel real. Câmpurile dintr-o vizualizare (view) sunt câmpuri dintr-una sau mai multe tabele reale din baza de date.
Puteți adăuga funcții SQL, WHERE și instrucțiuni JOIN într-o vizualizare (view) și prezentați datele ca și cum datele proveneau dintr-un singur tabel.
Sintaxă CREATE VIEW
CREATE VIEW view_name AS
SELECT column1, column2, ...
FROM table_name
WHERE condition;
O vizualizare (view) afișează întotdeauna date actualizate! Motorul bazei de date recreează datele, folosind instrucțiunea SQL a vizualizării (view), de fiecare dată când un utilizator solicită o vizualizare (view).
Exemple SQL CREATE VIEW
Următorul SQL creează o vizualizare (view) care arată toți clienții (customers) din Brazilia:
CREATE VIEW [Brazilia Customers] AS
SELECT CustomerName, ContactName
FROM Customers
WHERE Country = "Brazilia";
Putem consulta întrebarea de mai sus după cum urmează:
SELECT * FROM [Brazilia Customers];
Următorul SQL creează o vizualizare (view) care selectează fiecare produs din tabelul „Produse” (Products) cu un preț mai mare decât prețul mediu:
CREATE VIEW [Products Above Average Price] AS
SELECT ProductName, Price
FROM Products
WHERE Price > (SELECT AVG(Price) FROM Products);
Putem consulta întrebarea de mai sus după cum urmează:
SELECT * FROM [Products Above Average Price];
SQL Actualizarea unei vizualizări (SQL Updating a View)
O vizualizare (view) poate fi actualizată cu comanda CREATE SAU REPLACE VIEW.
Sintaxă SQL CREATE SAU REPLACE VIEW
CREATE OR REPLACE VIEW view_name AS
SELECT column1, column2, ...
FROM table_name
WHERE condition;
Următorul SQL adaugă coloana „Oraș” (City) la vizualizarea (view) „Clienții din Brazilia” (Brazilia Customers):
CREATE OR REPLACE VIEW [Brazil Customers] AS
SELECT CustomerName, ContactName, City
FROM Customers
WHERE Country = "Brazil";
SQL Eliminarea unei vizualizări (SQL Dropping a View)
O vizualizare (view) este ștersă cu comanda DROP VIEW.
Sintaxă SQL DROP VIEW
DROP VIEW view_name;
Următorul SQL renunță la vizualizarea (view) „Clienții din Brazilia” (Brazilia Customers):
DROP VIEW [Brazilia Customers];
SQL Injection
Injecția SQL (SQL Injection)
Injecția SQL (SQL Injection) este o tehnică de injecție de cod (code injection) care ar putea distruge baza de date.
Injecția SQL (SQL Injection) este una dintre cele mai frecvente tehnici de hacking web.
Injecția SQL (SQL Injection) este plasarea codului rău intenționat în declarațiile SQL, prin introducerea paginii web.
SQL în paginile web
Injecția SQL (SQL Injection) are loc de obicei atunci când ceri utilizatorului o introducere, cum ar fi numele său de utilizator / userid (username/userid), iar în loc de nume / id (name/id), utilizatorul vă oferă o declarație SQL pe care o veți rula în mod neștiut pe baza de date.
Uitați-vă la următorul exemplu care creează o instrucțiune SELECT adăugând o variabilă (txtUserId) la un șir selectat. Variabila este preluată din intrarea utilizatorului (getRequestString):
txtUserId = getRequestString("UserId");
txtSQL = "SELECT * FROM Users WHERE UserId = " + txtUserId;
Restul acestui capitol descrie pericolele potențiale ale utilizării intrării utilizatorului în declarațiile SQL.
Injecția SQL pe baza 1 = 1 este întotdeauna adevărată
Privește din nou exemplul de mai sus. Scopul inițial al codului a fost crearea unei instrucțiuni SQL pentru a selecta un utilizator, cu un id de utilizator (user id) dat.
Dacă nu există nimic care să împiedice un utilizator să introducă o intrare „greșită” (wrong), utilizatorul poate introduce unele intrări „inteligente” (smart) ca aceasta:
UserId: 105 SAU 1 = 1
Apoi, instrucțiunea SQL va arăta astfel:
SELECT * FROM Users WHERE UserId = 105 OR 1=1;
SQL-ul de mai sus este valid și va întoarce TOATE (ALL) rândurile din tabelul „Utilizatori” (Users), deoarece OR 1 = 1 este întotdeauna TRUE.
Exemplul de mai sus pare periculos? Ce se întâmplă dacă tabelul „Utilizatori” (Users) conține nume și parole?
Instrucțiunea SQL de mai sus este la fel ca aceasta:
SELECT UserId, Name, Password FROM Users WHERE UserId = 105 or 1=1;
Un hacker ar putea avea acces la toate numele de utilizator și parolele (user names și passwords) dintr-o bază de date, introducând pur și simplu 105 OR 1 = 1 în câmpul de introducere.
Injecția SQL Bazată pe "" = "" este întotdeauna adevărată
Iată un exemplu de autentificare a utilizatorului pe un site web:
Nume utilizator: John Doe
Parola: myPass
Exemplu:
uName = getRequestString("username");
uPass = getRequestString("userpassword");
sql = 'SELECT * FROM Users WHERE Name ="' + uName + '" AND Pass ="' + uPass + '"'
Rezultat:
SELECT * FROM Users WHERE Name ="John Doe" AND Pass ="myPass"
Un hacker ar putea avea acces la numele de utilizator și parolele (user names și passwords) dintr-o bază de date, introducând pur și simplu "OR" "=" în caseta de text a numelui de utilizator sau a parolei (user name sau password):
Nume utilizator: "sau" "="
Parola: "sau" "="
Codul de la server va crea o declarație SQL validă astfel:
Rezultat:
SELECT * FROM Users WHERE Name ="" or ""="" AND Pass ="" or ""=""
SQL de mai sus este valid și va returna toate rândurile din tabelul „Utilizatori” (Users), deoarece OR „„ = „„ este întotdeauna TRUE.
Injecție SQL bazată pe declarații SQL Batched (SQL Injection Based on Batched SQL Statements)
Majoritatea bazelor de date acceptă declarația SQL batched.
Un batch (lot) de instrucțiuni SQL este un grup de două sau mai multe instrucțiuni SQL, separate prin punct și virgulă.
Instrucțiunea SQL de mai jos va returna toate rândurile din tabelul „Utilizatori” (Users), apoi va șterge tabelul „Furnizori” (Suppliers).
SELECT * FROM Users; DROP TABLE Suppliers
txtUserId = getRequestString("UserId");
txtSQL = "SELECT * FROM Users WHERE UserId = " + txtUserId;
User id: 105; DROP TABLE Suppliers
SELECT * FROM Users WHERE UserId = 105; DROP TABLE Suppliers;
Utilizați parametrii SQL pentru protecție
Pentru a proteja un site web de injecția SQL, puteți utiliza parametrii SQL.
Parametrii SQL sunt valori care sunt adăugate la o interogare SQL la momentul executării, într-o manieră controlată.
Exemplu Razor ASP.NET:
txtUserId = getRequestString("UserId");
txtSQL = "SELECT * FROM Users WHERE UserId = @0";
db.Execute(txtSQL,txtUserId);
Rețineți că parametrii sunt reprezentați în instrucțiunea SQL de către un marker@.
Motorul SQL verifică fiecare parametru pentru a se asigura că este corect pentru coloana sa și sunt tratate literal, și nu ca parte a SQL-ului care trebuie executat.
txtNam = getRequestString("CustomerName");
txtAdd = getRequestString("Address");
txtCit = getRequestString("City");
txtSQL = "INSERT INTO Customers (CustomerName,Address,City) Values(@0,@1,@2)";
db.Execute(txtSQL,txtNam,txtAdd,txtCit);
Următoarele exemple arată cum să construiți interogări parametrizate în unele limbaje web comune.
SELECTAȚI DECLARAȚIA ÎN ASP.NET:
txtUserId = getRequestString("UserId");
sql = "SELECT * FROM Customers WHERE CustomerId = @0";
command = new SqlCommand(sql);
command.Parameters.AddWithValue("@0",txtUserID);
command.ExecuteReader();
INSERAȚI ÎN DECLARAȚIE ÎN ASP.NET:
txtNam = getRequestString("CustomerName");
txtAdd = getRequestString("Address");
txtCit = getRequestString("City");
txtSQL = "INSERT INTO Customers (CustomerName,Address,City) Values(@0,@1,@2)";
command = new SqlCommand(txtSQL);
command.Parameters.AddWithValue("@0",txtNam);
command.Parameters.AddWithValue("@1",txtAdd);
command.Parameters.AddWithValue("@2",txtCit);
command.ExecuteNonQuery();
INSERAȚI ÎN DECLARAȚIE ÎN PHP:
$stmt = $dbh->prepare("INSERT INTO Customers (CustomerName,Address,City)
VALUES (:nam, :add, :cit)");
$stmt->bindParam(':nam', $txtNam);
$stmt->bindParam(':add', $txtAdd);
$stmt->bindParam(':cit', $txtCit);
$stmt->execute();
SQL Găzduire
SQL Găzduire (SQL Hosting)
Dacă doriți ca site-ul dvs. web să poată stoca și prelua date dintr-o bază de date, serverul dvs. web ar trebui să aibă acces la o bază de date (database-system) care utilizează limbajul SQL.
Dacă serverul dvs. web este găzduit de un furnizor de servicii Internet ( Internet Service Provider) (ISP), va trebui să căutați planuri de găzduire SQL (SQL hosting).
Cele mai frecvente baze de date de găzduire SQL (SQL hosting databases) sunt MS SQL Server, Oracle, MySQL și MS Access.
MS SQL Server
Microsoft SQL Server este un software popular de bază de date pentru site-uri web bazate pe baze de date (database-driven) cu trafic ridicat.
SQL Server este un sistem de baze de date SQL (SQL database system) foarte puternic, robust și complet prezentat.
Oracle
Oracle este, de asemenea, un software popular de baze de date pentru site-uri web bazate pe baze de date cu trafic ridicat.
Oracle este un sistem de baze de date SQL foarte puternic, robust și complet prezentat.
MySQL
MySQL este, de asemenea, un software popular de baze de date pentru site-uri web.
MySQL este un sistem de baze de date SQL foarte puternic, robust și complet caracterizat.
MySQL este o alternativă ieftină la soluțiile scumpe Microsoft și Oracle.
Access
Când un site web necesită doar o bază de date simplă, Microsoft Access poate fi o soluție.
Access-ul nu este potrivit pentru traficul foarte ridicat și nu este la fel de puternic ca MySQL, SQL Server sau Oracle.
PHP Introducere
PHP Introducere
Codul PHP este executat pe server.
HTML
CSS
JavaScript
Ce este PHP?
PHP este un acronim pentru "PHP: Hypertext Preprocessor"
PHP este un limbaj de scripturi de surse deschise, utilizat pe scară largă
Scripturile PHP sunt executate pe server
PHP se poate descărca și utiliza gratuit
PHP este un limbaj uimitor și popular!
Este suficient de puternic pentru a fi în centrul celui mai mare sistem de blogging de pe web (WordPress)!
Este suficient de adânc pentru a rula cea mai mare rețea de socializare (Facebook)!
Ce poate face PHP?
PHP poate genera conținut dinamic al paginii
PHP poate crea, deschide, citi, scrie, șterge și închide fișiere pe server
PHP poate colecta date de formular
PHP poate trimite și primi cookie-uri
PHP poate adăuga, șterge, modifica date din baza de date
PHP poate fi utilizat pentru a controla accesul utilizatorului
PHP poate cripta dateCu PHP nu ești limitat la output HTML. Puteți output imagini, fișiere PDF și chiar filme Flash. De asemenea, puteți output orice text, cum ar fi XHTML și XML.
De ce PHP?
PHP rulează pe diverse platforme (Windows, Linux, Unix, Mac OS X etc.)
PHP este compatibil cu aproape toate serverele folosite astăzi (Apache, IIS etc.)
PHP acceptă o gamă largă de baze de date
PHP este gratuit. Descărcați-l din resursa oficială PHP: www.php.net
PHP este ușor de învățat și rulează eficient pe serverCe este nou în PHP 7
PHP 7 este mult mai rapid decât versiunea stabilă și populară anterioară(PHP 5.6)
PHP 7 a îmbunătățit gestionarea erorilor
PHP 7 acceptă declarații de tip (Type Declarations) mai stricte pentru argumentele funcției
PHP 7 acceptă operatori noi (cum ar fi operatorul național spațial: <=>)
PHP Instalare
Instalare PHP
De ce am nevoie?
Pentru a începe să utilizați PHP, puteți sa:
Găsiți o gazdă web (web host) cu suport PHP și MySQL
Instalați un server web (web server) pe propriul computer, apoi instalați PHP și MySQL
Utilizați o gazdă web (web host) cu suport PHP
Dacă serverul dvs. a activat suportul pentru PHP, nu trebuie să faceți nimic.
Creează doar câteva fișiere .php, le plasează în directorul tău web și serverul le va analiza automat pentru tine.
Nu este necesar să compilați nimic sau să instalați instrumente suplimentare.
Deoarece PHP este gratuit, majoritatea gazdelor web (web host) oferă suport PHP.
Configurați PHP pe propriul computer
Cu toate acestea, dacă serverul dvs. nu acceptă PHP, trebuie să:
instalați un server web
instalați PHP
instalați o bază de date, cum ar fi MySQL
Site-ul oficial PHP (PHP.net) are instrucțiuni de instalare pentru PHP: http://php.net/manual/en/install.php
PHP Sintaxă
Sintaxă PHP
Un script PHP este executat pe server, iar un simplu rezultat HTML este trimis înapoi în browser.
Sintaxa PHP de bază
Un script PHP poate fi plasat oriunde în document.
Un script PHP începe cu <?php și se termină cu?>:
<?php
// Codul PHP se introduce aici
?>
Extensia implicită pentru fișierele PHP este „.php”.
În mod normal, un fișier PHP conține etichete HTML și unele coduri de scripturi PHP (PHP scripting code).
Mai jos, avem un exemplu de fișier PHP simplu, cu un script PHP care folosește funcția PHP încorporată „echo” pentru a scoate textul „Hello World!” pe o pagină web:
Exemplu
<!DOCTYPE html>
<html>
<body>
<h1>My first PHP page</h1>
<?php
echo "Hello World!";
?>
</body>
</html>
Instrucțiunile PHP se termină cu punct și virgulă (;).
PHP Case Sensitivity
În PHP, NU există cuvinte cheie (de exemplu, if, else, while, echo etc.), clasele, funcțiile și funcțiile definite de utilizator (classes, functions, and user-defined functions) sunt case-sensitive.
În exemplul de mai jos, toate cele trei declarații echo sunt egale și legale:
<!DOCTYPE html>
<html>
<body>
<?php
ECHO "Hello World!<br>";
echo "Hello World!<br>";
EcHo "Hello World!<br>";
?>
</body>
</html>
Cu toate acestea; toate numele de variabile sunt case-sensitive!
Priviți exemplul de mai jos; numai prima declarație va afișa valoarea variabilei $color! Acest lucru se datorează faptului că $color, $COLOR și $coLOR sunt tratate ca trei variabile diferite:
<!DOCTYPE html>
<html>
<body>
<?php
$color = "red";
echo "Mașina mea este " . $color . "<br>";
echo "Casa mea este " . $COLOR . "<br>";
echo "Barca mea este " . $coLOR . "<br>";
?>
</body>
</html>
PHP Comentarii
Comentarii în PHP
Un comentariu în cod PHP este o linie care nu este executată ca parte a programului. Singurul său scop este să fie citit de cineva care se uită la cod.
Comentariile pot fi folosite pentru:
Lasă-i pe alții să înțeleagă codul tău
Reamintește-ți ce ai făcut - Majoritatea programatorilor s-au confruntat cu revenirea la propria muncă un an sau doi mai târziu și trebuie să-și dea seama ce au făcut. Comentariile îți pot aminti la ce te gândeai când ai scris codul
PHP acceptă mai multe moduri de a comenta:
Sintaxă pentru comentarii cu o singură linie (single-line comment):
<!DOCTYPE html>
<html>
<body>
<?php
// Acesta este un comentariu cu o singură linie (single-line comment)
# Acesta este, de asemenea, un comentariu cu o singură linie (single-line comment)
?>
</body>
</html>
Sintaxa pentru comentarii cu mai multe linii (multiple-line comments):
<!DOCTYPE html>
<html>
<body>
<?php
/*
Acesta este un block de comentarii cu mai multe linii (multiple-lines comment block)
care se întinde pe multiple linii
*/
?>
</body>
</html>
Folosire comentarii pentru a lăsa părți din cod:
<!DOCTYPE html>
<html>
<body>
<?php
// De asemenea, puteți utiliza comentarii pentru a lăsa părți dintr-o linie de cod
$x = 5 /* + 15 */ + 5;
echo $x;
?>
</body>
</html>
PHP Variabile
Variabile PHP
Variabilele sunt „containere” (containers) pentru stocarea informațiilor.
Crearea (declararea) variabilelor PHP
În PHP, o variabilă începe cu semnul $, urmată de numele variabilei:
<?php
$txt = "Hello world!";
$x = 5;
$y = 10.5;
?>
După executarea declarațiilor de mai sus, variabila $txt va păstra valoarea "Hello world!", variabila $x va deține valoarea 5, iar variabila $y va păstra valoarea 10.5.
Când atribuiți o valoare text unei variabile, puneți ghilimele în jurul valorii.
Spre deosebire de alte limbaje de programare, PHP nu are nicio comandă pentru declararea unei variabile. Este creat în momentul în care i-ați atribuit prima dată o valoare.
Gândiți-vă la variabile ca la containere pentru stocarea datelor (containers for storing data).
Variabile PHP
O variabilă poate avea un nume scurt (cum ar fi x și y) sau un nume mai descriptiv (age, carname, total_volum).
Reguli pentru variabilele PHP:
O variabilă începe cu semnul $, urmată de numele variabilei.
Un nume de variabilă trebuie să înceapă cu o literă sau un caracter de subliniere.
Un nume de variabilă nu poate începe cu un număr.
Un nume de variabilă nu poate conține decât caractere alfa-numerice și underscores (A-z, 0-9 și _).
Denumirile variabilelor sunt case-sensitive ($age și $AGE sunt două variabile diferite).
Amintiți-vă că numele variabilei PHP sunt case-sensitive!
Variabile de ieșire (Output Variables)
Declarația PHP echo este adesea folosită pentru a afișa (output) date pe ecran.
Afișare (output) text și o variabilă:
<?php
$txt = "lectii-virtuale.ro";
echo "Îmi place $txt!";
?>
Următorul exemplu va produce aceeași ieșire (output) ca exemplul de mai sus:
<?php
$txt = "lectii-virtuale.ro";
echo "Îmi place " . $txt . "!";
?>
Următorul exemplu va produce suma a două variabile:
<?php
$x = 5;
$y = 4;
echo $x + $y;
?>
PHP este un limbaj tiparit mai puțin
În exemplul precedent, observați că nu trebuie să îi spunem PHP-ului ce tip de dată (data type) este variabila.
PHP asociază automat un tip de date (data type) variabilei, în funcție de valoarea acesteia. Deoarece tipurile de date (data types) nu sunt setate într-un sens strict, puteți face lucruri precum adăugarea unui șir la un număr întreg fără a provoca o eroare.
În PHP 7, au fost adăugate declarații de tip (type declarations). Aceasta oferă o opțiune de a specifica tipul de date (data type) preconizat la declararea unei funcții și, activând cerința strictă, va arunca o „eroare fatală” (Fatal Error) pe o nepotrivire de tip (type mismatch).
Veți afla mai multe despre cerințele stricte și non-stricte și declarațiile de tip de date din capitolul Funcții PHP.
Domeniul variabilelor PHP
În PHP, variabilele pot fi declarate oriunde în script.
Domeniul de aplicare al unei variabile este partea scriptului unde variabila poate fi referită / folosită (referenced/used).
PHP are trei domenii diferite de variabile : local, global, static.
Domeniul global și local
O variabilă declarată în afara unei funcții are un DOMENIU GLOBAL (GLOBAL SCOPE) și poate fi accesată numai în afara unei funcții:
Variabilă cu sfera globală:
<?php
$x = 5; // sfera globală
function myTest() {
// folosirea x în interiorul acestei funcții va genera o eroare
echo "<p>Variabila x în interiorul funcției este: $x</p>";
}
myTest();
echo "<p>Variabila x din exteriorul funcției este : $x</p>";
?>
O variabilă declarată în cadrul unei funcții are un SCOP LOCAL și poate fi accesată numai în cadrul acestei funcții:
Variabilă cu scop local:
<?php
function myTest() {
$x = 5; // scop local
echo "<p>Variabila x din interiorul funcției este: $x</p>";
}
myTest();
// folosirea x în afara funcției va genera o eroare
echo "<p>Variabila x din afara funcției este: $x</p>";
?>
Puteți avea variabile locale cu același nume în funcții diferite, deoarece variabilele locale sunt recunoscute doar de funcția în care sunt declarate.
Cuvântul cheie global (global keyword) este utilizat pentru a accesa o variabilă globală dintr-o funcție.
Pentru a face acest lucru, utilizați înainte de variabile (în interiorul funcției) cuvântul cheie global (global keyword):
<?php
$x = 5;
$y = 10;
function myTest() {
global $x, $y;
$y = $x + $y;
}
myTest();
echo $y; // outputs 15 (15 ieșiri)
?>
PHP stochează de asemenea toate variabilele globale într-un tablou numit $GLOBALS [index]. Indicele conține numele variabilei. Acest tablou este de asemenea accesibil din funcții și poate fi utilizat pentru a actualiza direct variabilele globale.
Exemplul de mai sus poate fi rescris astfel:
<?php
$x = 5;
$y = 10;
function myTest() {
$GLOBALS['y'] = $GLOBALS['x'] + $GLOBALS['y'];
}
myTest();
echo $y; // outputs 15 (15 ieșiri)
?>
PHP Cuvântul cheie static
În mod normal, când o funcție este finalizată / executată (completed/executed), toate variabilele sale sunt șterse. Cu toate acestea, uneori dorim ca o variabilă locală să NU fie ștearsă. Avem nevoie de asta pentru un alt job.
Pentru a face acest lucru, utilizați cuvântul cheie static (static keyword) când declarați pentru prima dată variabila:
<?php
function myTest() {
static $x = 0;
echo $x;
$x++;
}
myTest();
myTest();
myTest();
?>
Apoi, de fiecare dată când se apelează funcția, acea variabilă va avea în continuare informațiile pe care le conține din ultima dată când a fost apelată funcția.
Pentru funcție, variabila este încă locală.
PHP echo și print
Declarații PHP echo și print
Cu PHP, există două modalități de bază pentru a obține rezultate: echo și print.
În acest tutorial folosim echo sau print în aproape fiecare exemplu.
Declarații PHP echo și print
echo și print sunt la fel mai mult sau mai puțin. Ambele sunt folosite pentru a emite date pe ecran.
Diferențele sunt mici: echo nu are o valoare returnată în timp ce print are o valoare returnată 1, astfel încât să poată fi folosită în expresii. echo poate lua mai mulți parametri (deși o astfel de utilizare este rară) în timp ce print poate lua un argument. echo este marginal mai rapid decât print.
Declarația echo PHP
Instrucțiunea echo poate fi folosită cu sau fără paranteze: echo sau echo().
Afișați textul
Următorul exemplu arată cum să afișați (output) text cu comanda echo (observați că textul poate conține marcaj HTML):
<?php
echo "<h2>PHP is Fun!</h2>";
echo "Hello world!<br>";
echo "Sunt pe cale să învăț PHP! <br>";
echo "Acest ", "string ", "a fost ", "făcut ", "cu mai mulți parametri.";
?>
Afișați variabile
Următorul exemplu arată cum să afișați (output) text și variabile cu declarația echo:
<?php
$txt1 = "Învățați PHP";
$txt2 = "lectii-virtuale.ro";
$x = 5;
$y = 4;
echo "<h2>" . $txt1 . "</h2>";
echo "Studiu PHP at " . $txt2 . "<br>";
echo $x + $y;
?>
Declarația PHP print
Instrucțiunea print poate fi folosită cu sau fără paranteze: print sau print().
Afișați textul
Următorul exemplu arată cum să afișați (output) text cu comanda print (observați că textul poate conține marcaj HTML):
<?php
print "<h2>PHP is Fun!</h2>";
print "Hello world!<br>";
print "Sunt pe cale să învăț PHP!";
?>
Afișați variabile
Următorul exemplu arată cum să afișați (output) text și variabile cu instrucțiunea print:
<?php
$txt1 = "Învățați PHP";
$txt2 = "W3Schools.com";
$x = 5;
$y = 4;
print "<h2>" . $txt1 . "</h2>";
print "Studiați PHP la " . $txt2 . "<br>";
print $x + $y;
?>
PHP Tipuri de date
Tipuri de date PHP(PHP Data Types)
Variabilele pot stoca date de diferite tipuri și diferite tipuri de date pot face lucruri diferite.
PHP acceptă următoarele tipuri de date: String, Integer, Float (floating point numbers - numit și dublu), Boolean, Array, Object, NULL, Resource.
PHP String
Un string este o secvență de caractere, cum ar fi „Hello world!”.
Un string poate fi orice text din ghilimele. Puteți utiliza ghilimele simple sau duble:
<?php
$x = "Hello world!";
$y = 'Hello world!';
echo $x;
echo "<br>";
echo $y;
?>
PHP Integer
Un tip de date întreg (integer data type) este un număr non-zecimal cuprins între -2 147.483.648 și 2.147.483.647.
Reguli pentru numere întregi (integers):
Un număr întreg (integer) trebuie să aibă cel puțin o cifră
Un număr întreg (integer) nu trebuie să aibă o zecimală
Un număr întreg (integer) poate fi pozitiv sau negativ
Numerele întregi (integers) pot fi specificate în: zecimal (baza 10), hexazecimal (baza 16), octal (baza 8) sau notare binară (baza 2)
În următorul exemplu $ x este un număr întreg (integer). Funcția PHP var_dump() returnează tipul (data type) și valoarea datelor:
<?php
$x = 5985;
var_dump($x);
?>
PHP Float
Un float (număr flotant) este un număr cu punct zecimal sau un număr în formă exponențială.
În exemplul următor $x este un float. Funcția PHP var_dump() returnează tipul (data type) și valoarea datelor:
<?php
$x = 10.365;
var_dump($x);
?>
PHP Boolean
Un boolean reprezintă două stări posibile: TRUE sau FALSE.
$x = true;
$y = false;
Booleans sunt adesea folosiți în testarea condiționată. Veți afla mai multe despre testarea condiționată într-un capitol ulterior al acestui tutorial.
PHP Array
Un array (tablou) stochează mai multe valori într-o singură variabilă.
În următorul exemplu $cars este un array (tablou) . Funcția PHP var_dump() returnează tipul (data type) și valoarea datelor:
<?php
$cars = array("Volvo","BMW","Toyota");
var_dump($cars);
?>
PHP Object
Un object (obiect) este un tip de date (data type) care stochează date și informații despre modul de procesare a acestor date.
În PHP, un object (obiect) trebuie declarat explicit.
Mai întâi trebuie să declaram o clasă de obiect (class of object). Pentru aceasta, folosim cuvântul cheie class (class keyword). O clasă (class) este o structură care poate conține proprietăți și metode:
<?php
class Car {
function Car() {
$this->model = "VW";
}
}
// creați un obiect (object)
$herbie = new Car();
// arată proprietățiile obiectului (object)
echo $herbie->model;
?>
PHP NULL Value
Null este un tip de date special care poate avea o singură valoare: NULL.
O variabilă de tip de date (data type) NULL este o variabilă care nu are nicio valoare atribuită.
Dacă o variabilă este creată fără valoare, i se atribuie automat o valoare de NULL.
Variabilele pot fi de asemenea golite prin setarea valorii la NULL:
<?php
$x = "Hello world!";
$x = null;
var_dump($x);
?>
PHP Resource
Tipul resursei speciale nu este un tip de date (data type) real. Este stocarea unei referințe la funcții și resurse externe PHP.
Un exemplu obișnuit de utilizare a tipului de date resurse (resource data type) este un apel la baza de date.
PHP String
Un string (șir) este o secvență de caractere, precum „Hello world!”.
Funcții PHP String
În acest capitol vom analiza unele funcții utilizate frecvent pentru manipularea string-urilor (șirurilor).
strlen() - întoarce lungimea unui string (șir)
Funcția PHP strlen() returnează lungimea unui string (șir).
Întoarceți lungimea string-ului (șirului) „Hello world!”:
<?php
echo strlen("Hello world!"); // outputs 12 (12 ieșiri)
?>
str_word_count() - Numără cuvintele într-un string (șir)
Funcția PHP str_word_count() numără numărul de cuvinte dintr-un string (șir).
Numărați numărul de cuvinte din string-ul (șirul) „Hello world!”:
<?php
echo str_word_count("Hello world!"); // outputs 2 (2 ieșiri)
?>
strrev() - inversează un string (șir)
Funcția PHP strrev() inversează un string (șir).
Inversați string- ul (șirul) „Hello world!”:
<?php
echo strrev("Hello world!"); // outputs !dlrow olleH (ieșiri! dlrow olleH)
?>
strpos() - Căutați un text într-un string (șir)
Funcția PHP strpos() caută un text specific într-un string (șir). Dacă se găsește o potrivire, funcția returnează poziția caracterului primei potriviri. Dacă nu se găsește nicio potrivire, aceasta va returna FALSE.
Căutați textul „world” în string-ul (șirul) „Hello world!”:
<?php
echo strpos("Hello world!", "world"); // outputs 6 (6 ieșiri)
?>
Prima poziție a caracterelor dintr-un string (șir) este 0 (nu 1).
str_replace() - Înlocuiți textul într-un string (șir)
Funcția PHP str_replace() înlocuiește unele caractere cu alte caractere dintr-un string (șir).
Înlocuiți textul „world” cu „Dolly”:
<?php
echo str_replace("world", "Dolly", "Hello world!"); // outputs Hello Dolly! (ieșiri Hello Dolly!)
?>
Referință completă PHP pentru string-uri (șiruri)
Referința string-ului (șirului) PHP conține descrierea și exemplul de utilizare, pentru fiecare funcție!
PHP Numere
PHP Numbers
În acest capitol vom analiza în profunzime Integers, Floats și Number Strings.
Numere PHP
Un lucru de remarcat cu privire la PHP este că oferă conversie automată de tip de date (automatic data type conversion).
Deci, dacă atribuiți o valoare integer (valoare întreagă) unei variabile, tipul acelei variabile va fi automat un integer (număr întreg). Apoi, dacă atribuiți un string (șir) aceleiași variabile, tipul se va schimba la un string (șir).
Această conversie automată îți poate sparge codul.
PHP Integers
Un integer (număr întreg) este un număr fără nicio parte zecimală.
2, 256, -256, 10358, -179567 sunt integers (întregi). În timp ce 7.56, 10.0, 150.67 sunt floats.
Deci, un tip de date întreg (integer data type) este un număr non-zecimal cuprins între -2147483648 și 2147483647. O valoare mai mare (sau mai mică) decât aceasta, va fi stocată ca float, deoarece depășește limita unui integer (număr întreg).
Un alt lucru important de știut este că, chiar dacă 4*2,5 este 10, rezultatul este stocat sub formă de float, deoarece unul dintre operanzi este un float (2.5).
Iată câteva reguli pentru integers (numere întregi):
Un număr întreg (integer) trebuie să aibă cel puțin o cifră
Un număr întreg (integer) nu trebuie să aibă o zecimală
Un număr întreg (integer) poate fi pozitiv sau negativ
Numerele întregi pot fi specificate în trei formate: zecimale (baza 10), hexazecimale (baza 16 - prefix 0x) sau octale (baza 8 - prefix 0)
PHP are următoarele funcții pentru a verifica dacă tipul unei variabile este integer (întreg):
is_int()
is_integer() - alias of is_int()
is_long() - alias of is_int()
Verificați dacă tipul unei variabile este integer (întreg):
<?php
$x = 5985;
var_dump(is_int($x));
$x = 59.85;
var_dump(is_int($x));
?>
PHP Floats
Un float este un număr cu un punct zecimal sau un număr în formă exponențială.
2.0, 256.4, 10.358, 7.64E + 5, 5.56E-5 sunt toate floats.
Tipul de date (data type) float poate stoca de obicei o valoare de până la 1.7976931348623E + 308 (dependentă de platformă) și are o precizie maximă de 14 cifre.
PHP are următoarele funcții pentru a verifica dacă tipul unei variabile este float:
is_float()
is_double() - alias of is_float()
Verificați dacă tipul unei variabile este float:
<?php
$x = 10.365;
var_dump(is_float($x));
?>
PHP Infinity
O valoare numerică mai mare decât PHP_FLOAT_MAX este considerată infinită.
PHP are următoarele funcții pentru a verifica dacă o valoare numerică este finită sau infinită:
is_finite()
is_infinite()
Cu toate acestea, funcția PHP var_dump() returnează tipul (data type) și valoarea datelor:
Verificați dacă o valoare numerică este finită sau infinită:
<?php
$x = 1.9e411;
var_dump($x);
?>
PHP NaN
NaN semnifică Not Number.
NaN este utilizat pentru operații matematice imposibile.
PHP are următoarele funcții pentru a verifica dacă o valoare nu este un număr:
is_nan()
Cu toate acestea, funcția PHP var_dump() returnează tipul și valoarea datelor:Calculul invalid va returna o valoare NaN:
<?php
$x = acos(8);
var_dump($x);
?>
PHP Numerical Strings
Funcția PHP is_numeric() poate fi utilizată pentru a afla dacă o variabilă este numerică. Funcția returnează true dacă variabila este un număr sau un șir numeric, false altfel.
Verificați dacă variabila este numerică:
<?php
$x = 5985;
var_dump(is_numeric($x));
$x = "5985";
var_dump(is_numeric($x));
$x = "59.85" + 100;
var_dump(is_numeric($x));
$x = "Hello";
var_dump(is_numeric($x));
?>
De la PHP 7.0: Funcția is_numeric() va returna FALSE pentru șirurile numerice (numeric strings) în formă hexazecimală (de exemplu, 0xf4c3b00c), deoarece nu mai sunt considerate șiruri numerice (numeric strings).
PHP Casting Strings and Floats to Integers
Uneori, trebuie să convertiți o valoare numerică într-un alt tip de date (data type).
Funcția (int), (integer) sau intval() sunt adesea folosite pentru a converti o valoare (value) într-un număr întreg (integer).
Convertiți float și string la integer:
<?php
// Cast float to int
$x = 23465.768;
$int_cast = (int)$x;
echo $int_cast;
echo "<br>";
// Cast string to int
$x = "23465.768";
$int_cast = (int)$x;
echo $int_cast;
?>
PHP Constante
Constante PHP
Constantele sunt ca variabilele, cu excepția faptului că, odată definite, nu pot fi modificate sau nedefinite.
Constante PHP
O constantă este un identificator (nume) pentru o valoare simplă. Valoarea nu poate fi modificată în timpul scriptului.
Un nume constant valabil începe cu o literă sau underscore (fără semn $ înainte de numele constant).
Spre deosebire de variabile, constantele sunt automat globale pe întregul script.
Creați o constantă PHP
Pentru a crea o constantă, utilizați funcția define().
Sintaxă
define(name, value, case-insensitive)
Parametrii:
name: Specifică numele constantei.
value: Specifică valoarea constantei.
case-insensitive: Specifică dacă numele constant trebuie să fie case-insensitive. Implicit este fals.
Creați o constantă cu un nume case-sensitive :
<?php
define("SALUT", "Bine ați venit la lectii-virtuale.ro!");
echo SALUT;
?>
Creați o constantă cu un nume sensibil case-insensitive:
<?php
define("SALUT", "Bine ați venit la lectii-virtuale.ro!", true);
echo salut;
?>
PHP Constant Arrays
În PHP7, puteți crea o constantă Array folosind funcția define().
Creați o constantă Array:
<?php
define("cars", [
"Alfa Romeo",
"BMW",
"Toyota"
]);
echo cars[0];
?>
Constantele sunt globale
Constantele sunt automat globale și pot fi utilizate pe întregul script.
Acest exemplu utilizează o constantă în interiorul unei funcții, chiar dacă este definită în afara funcției:
<?php
define("SALUT", "Bine ați venit la lectii-virtuale.ro!");
function myTest() {
echo SALUT;
}
myTest();
?>
PHP Operatori
Operatori PHP
Operatorii sunt folosiți pentru a efectua operații cu variabile și valori.
PHP împarte operatorii în următoarele grupuri:
Operatori de aritmetică
Operatori de atribuire
Operatori de comparație
Operatori de creștere / descreștere
Operatori logici
Operatori cu șiruri (string)
Operatori de matrice (array)
Operatori de atribuire condiționată
Operatori Aritmetici PHP
Operatorii aritmetici PHP sunt folosiți cu valori numerice pentru a efectua operațiuni aritmetice comune, cum ar fi adunarea, scăderea, înmulțirea etc.
Operatori PHP de atribuire
Operatorii PHP de atribuire sunt folosiți cu valori numerice pentru a scrie o valoare a unei variabile.
Operatorul de atribuire de bază în PHP este "=". Înseamnă că operandul stâng este setat la valoarea expresiei de atribuire din dreapta.
Operatori PHP de comparație
Operatorii PHP de comparație sunt folosiți pentru a compara două valori (număr sau șir/number or string)
Operatori PHP de creștere / descreștere
Operatorii PHP de incrementare sunt folosiți pentru a crește valoarea unei variabile.
Operatorii PHP de descreștere sunt folosiți pentru a descrește valoarea unei variabile.
Operatori logici PHP
Operatorii logici PHP sunt folosiți pentru a combina instrucțiuni condiționale.
Operatori PHP String
PHP are doi operatori special conceputi pentru string-uri.
Operatori Array PHP
Operatorii Array PHP sunt folosiți pentru a compara matricile.
Operatori PHP de atribuire condiționată
Operatorii PHP de alocare condiționată sunt folosiți pentru a seta o valoare în funcție de condiții.
PHP if...else...elseif
Instrucțiunile PHP if...else...elseif
Instrucțiunile condiționale sunt utilizate pentru a efectua diferite acțiuni bazate pe condiții diferite.
Instrucțiuni condiționale PHP
Foarte des când scrieți cod, doriți să efectuați diferite acțiuni pentru diferite condiții. Pentru a face acest lucru puteți utiliza în codul dvs. instrucțiuni condiționale.
În PHP avem următoarele instrucțiuni condiționale:
if statement - execută unele coduri dacă o condiție este adevărată
if ... else statement - execută ceva cod dacă o condiție este adevărată și un alt cod dacă această condiție este falsă
if ... elseif ... else statement - execută coduri diferite pentru mai mult de două condiții
switch statement - selectează unul dintre numeroasele blocuri de cod care trebuie executate
PHP - Instrucțiunea if
Instrucțiunea if execută un cod dacă o condiție este adevărată.
Sintaxă
if (condition) {
cod care trebuie executat dacă condiția este adevărată (true);
}
<?php
$t = date("H");
if ($t < "20") {
echo "Să aveți o zi bună!";
}
?>
Instrucțiunea PHP - The if...else
Instrucțiunea if ... else execută un cod dacă o condiție este adevărată (true) și un alt cod dacă această condiție este falsă (false).
Sintaxă
if (condition) {
cod care trebuie executat dacă condiția este adevărată (true);
} else {
cod care trebuie executat dacă condiția este falsă (false);
}
<?php
$t = date("H");
if ($t < "20") {
echo "Să aveți o zi bună!";
} else {
echo "Noapte bună!";
}
?>
Instrucțiunea PHP - if...elseif...else
Instrucțiunea if ... elseif ... else execută coduri diferite pentru mai mult de două condiții.
Sintaxă
if (condition) {
cod care trebuie executat dacă această condiție este adevărată (true);
} elseif (condition) {
cod care trebuie executat dacă prima condiție este falsă (false) și această condiție este adevărată (true);
} else {
cod care trebuie executat dacă toate condițiile sunt false (false);
}
<?php
$t = date("H");
if ($t < "10") {
echo "Bună dimineața!";
} elseif ($t < "20") {
echo "Să aveți o zi bună!";
} else {
echo "Noapte bună!";
}
?>
Instrucțiunea PHP- switch
Instrucțiunea switch va fi explicată în capitolul următor.
PHP switch
Instrucțiunea PHP switch
Instrucțiunea switch este utilizată pentru a efectua diferite acțiuni bazate pe condiții diferite.
Instrucțiunea PHP switch
Utilizați instrucțiunea switch pentru a selecta unul dintre numeroasele blocuri de cod care urmează să fie executate.
Sintaxă
switch (n) {
case label1:
cod care trebuie executat dacă n=label1;
break;
case label2:
cod care trebuie executat dacă n=label2;
break;
case label3:
cod care trebuie executat dacă n=label3;
break;
...
default:
cod care trebuie executat dacă n este diferit de toate labels;
}
Așa funcționează: Mai întâi avem o singură expresie n (cel mai adesea o variabilă), care este evaluată o singură dată. Valoarea expresiei este apoi comparată cu valorile pentru fiecare caz din structură. Dacă există o potrivire, blocul de cod asociat cu acest caz este executat. Folosiți pauză pentru a împiedica automat rularea codului în următorul caz. Instrucțiunea implicită este utilizată dacă nu se găsește nicio potrivire.
<?php
$favcolor = "roșu";
switch ($favcolor) {
case "roșu":
echo "Culoarea ta preferată este roșu!";
break;
case "albastru":
echo "Culoarea ta preferată este albastru!";
break;
case "verde":
echo "Culoarea ta preferată este verde!";
break;
default:
echo "Culoarea ta preferată nu este nici roșu, nici albastru, nici verde!";
}
?>
PHP Loops
Bucle PHP (PHP Loops)
În capitolele următoare veți învăța cum să repetați codul folosind bucle (loops) în PHP.
Bucle PHP (PHP Loops)
Adesea, atunci când scrieți cod, doriți ca același block de cod să fie difuzat de mai multe ori un anumit număr de ori. Deci, în loc să adăugăm mai multe linii de cod aproape egale într-un script, putem folosi bucle (loops).
Buclele (loops) sunt utilizate pentru a executa același block de cod din nou și din nou, atâta timp cât o anumită condiție este adevărată (true).
În PHP, avem următoarele tipuri de buclă (loop types):
while - buclează (loops) un block de cod atâta timp cât condiția specificată este adevărată (true).
do ... while - se buclează (loops) o dată printr-un block de cod, apoi se repetă bucla (loop) atâta timp cât condiția specificată este adevărată (true).
for - se buclează (loops) printr-un block de cod de un număr specificat de ori.
foreach - se buclează (loops) printr-un block de cod pentru fiecare element dintr-un tablou.
Capitolele următoare vor explica și vor oferi exemple pentru fiecare tip de buclă (loop type).
PHP bucla while (PHP while Loop)
Bucla while - Bucle printr-un block de cod atâta timp cât condiția specificată este adevărată (true).
PHP bucla while
Bucla while execută un block de cod atâta timp cât condiția specificată este adevărată (true).
Sintaxă
while (condition is true) {
cod de executat;
}
<?php
$x = 1;
while($x <= 5) {
echo "Numărul este: $x <br>";
$x++;
}
?>
$x = 1; - Inițializați contorul de bucle (loop counter) ($x) și setați valoarea de pornire la 1.
$x <= 5 - Continuați bucla (loop) atâta timp cât $x este mai mică sau egală cu 5.
$X ++; - Măriți valoarea contorului buclei (loop counter) cu 1 pentru fiecare iterație.
<?php
$x = 0;
while($x <= 100) {
echo "Numărul este: $x <br>";
$x+=10;
}
?>
$x = 0; - Inițializați contorul buclei (loop counter) ($x) și setați valoarea de pornire la 0.
$x <= 100 - Continuați bucla (loop) atât timp cât $x este mai mic sau egal cu 100.
$X + = 10; - Măriți valoarea contorului buclei (loop counter) cu 10 pentru fiecare iterație.
PHP bucla do while (PHP do while Loop)
Bucla do ... while - Buclează (loops) o dată printr-un block de cod, apoi repetă bucla (loop) atâta timp cât condiția specificată este adevărată (true).
PHP bucla do while (PHP do while Loop)
Bucla do ... while va executa întotdeauna blocul de cod o dată, apoi va verifica starea și va repeta bucla (loop) cât timp (while) condiția specificată este adevărată (true).
Sintaxă
do {
cod de executat;
} while (condition is true);
Exemplul de mai jos stabilește prima variabilă $x la 1 ($x = 1). Apoi, bucla do while (do while loop) va scrie o anumită ieșire, apoi va crește variabila $x cu 1. Apoi, starea este bifată ($x este mai mică sau egală cu 5?), Iar bucla (loop) va continua să funcționeze atâta timp cât $x este mai mică sau egală cu 5:
<?php
$x = 1;
do {
echo "Numărul este: $x <br>";
$x++;
} while ($x <= 5);
?>
În bucla do...while (do...while loop) în timp ce condiția este testată DUPĂ executarea instrucțiunilor din buclă (loop). Aceasta înseamnă că bucla do ... while (do...while loop) își va executa instrucțiunile cel puțin o dată, chiar dacă condiția este falsă (false). Vezi exemplul de mai jos.
Acest exemplu stabilește variabila $x la 6, apoi rulează bucla (loop), apoi starea este verificată:
<?php
$x = 6;
do {
echo "Numărul este: $x <br>";
$x++;
} while ($x <= 5);
?>
PHP bucla for. (PHP for Loop)
Bucla for - Buclează (loops) printr-un block de cod de un număr specificat de ori.
PHP bucla for. (PHP for Loop)
Bucla for se utilizează atunci când știi în prealabil de câte ori ar trebui să ruleze scriptul.
Sintaxă
for (init counter; test counter; increment counter) {
cod care trebuie executat pentru fiecare iterație;
}
Parametrii:
init counter: Initializarea valorii contorului buclei (loop counter).
test counter: evaluare pentru fiecare iterație de buclă (loop iteration). Dacă se evaluează la TRUE, bucla (loop) continuă. Dacă se evaluează la FALSE, bucla (loop) se termină.
increment counter: Crește valoarea contorului buclei (loop counter).
Exemplul de mai jos afișează numerele de la 0 la 10:
<?php
for ($x = 0; $x <= 10; $x++) {
echo "Numărul este: $x <br>";
}
?>
$x = 0; - Inițializați contorul buclei (loop counter) ($x) și setați valoarea de pornire la 0.
$x <= 10; - Continuați bucla (loop) atâta timp cât $x este mai mic sau egal cu 10.
$x ++ - Măriți valoarea contorului buclei (loop counter) cu 1 pentru fiecare iterație.
Acest exemplu numără până la 100 din zece în zece:
<?php
for ($x = 0; $x <= 100; $x+=10) {
echo "Numărul este: $x <br>";
}
?>
$x = 0; - Inițializați contorul buclei (loop counter) ($x) și setați valoarea de pornire la 0.
$x <= 100; - Continuați bucla (loop) atâta timp cât $x este mai mic sau egal cu 100.
$x + = 10 - Măriți valoarea contorului buclei (loop counter) cu 10 pentru fiecare iterație.
PHP bucla foreach (PHP foreach Loop)
Bucla foreach - Buclează (loops) printr-un block de cod pentru fiecare element dintr-un tablou (array).
PHP bucla foreach (PHP foreach Loop)
Bucla foreach funcționează numai pe tablouri (arrays) și este utilizată pentru a bucla (loop) fiecare pereche cheie / valoare (key/value ) dintr-un tablou (array).
Sintaxă
foreach ($array as $value) {
cod de executat;
}
Pentru fiecare iterație de buclă (loop iteration), valoarea elementului array curent este atribuită lui $value, iar indicatorul tabloului (array) este mutat de unul singur până când ajunge la ultimul element de matrice (element array).
Următorul exemplu va emite valorile tabloului dat (array) ($colors):
<?php
$colors = array("red", "green", "blue", "yellow");
foreach ($colors as $value) {
echo "$value <br>";
}
?>
<?php
$age = array("Ion"=>"35", "Petre"=>"37", "Tudor"=>"43");
foreach($age as $x => $val) {
echo "$x = $val<br>";
}
?>
PHP Funcții
Funcții PHP
Puterea reală a PHP provine din funcțiile sale.
PHP are peste 1000 de funcții încorporate și, în plus, vă puteți crea propriile funcții personalizate.
Funcții încorporate în PHP (PHP Built-in Functions)
PHP are peste 1000 de funcții încorporate (built-in) care pot fi apelate direct, dintr-un script, pentru a efectua o sarcină specifică.
Funcții definite de utilizator în PHP
Pe lângă funcțiile PHP încorporate (built-in), este posibil să vă creați propriile funcții.
O funcție este un block de declarații care poate fi utilizat în mod repetat într-un program.
O funcție nu se va executa automat atunci când se încarcă o pagină.
O funcție va fi executată de un apel către funcție.
Creați o funcție definită de utilizator în PHP
O declarație de funcție definită de utilizator (user-defined function) începe cu funcția cuvânt:
Sintaxă
function functionName() {
cod de executat;
}
Un nume de funcție trebuie să înceapă cu o literă sau o subliniere (underscore).
Numele funcțiilor NU sunt case-sensitive.
Dați funcției un nume care să reflecte ceea ce face funcția!
În exemplul de mai jos, creem o funcție numită "writeMsg()". Paranteza ondulată de deschidere ({) indică începutul codului funcției, iar paranteza ondulată de închidere (}) indică sfârșitul funcției. Funcția întoarce (outputs ) „Hello world!”. Pentru a apela funcția, trebuie doar să scrieți numele ei urmată de paranteze ():
<?php
function writeMsg() {
echo "Hello world!";
}
writeMsg(); // apelați funcția
?>
Argumentele funcției PHP
Informațiile pot fi transmise funcțiilor prin argumente. Un argument este la fel ca o variabilă.
Argumentele sunt specificate după numele funcției, în interiorul parantezelor. Puteți adăuga oricâte argumente doriți, doar separați-le cu virgulă.
Următorul exemplu are o funcție cu un argument ($fname). Când se numește funcția familyName(), de asemenea, trecem de-a lungul unui nume (de exemplu, Ionescu) și numele este folosit în interiorul funcției, care produce (outputs) mai multe prenume diferite, dar un nume egal:
<?php
function familyName($fname) {
echo "$fname Refsnes.<br>";
}
familyName("Ionescu");
familyName("Popescu");
familyName("Georgescu");
familyName("Filipescu");
familyName("Zinescu");
?>
Următorul exemplu are o funcție cu două argumente ($fname și $year):
<?php
function familyName($fname, $year) {
echo "$fname Refsnes. Născut în $year <br>";
}
familyName("Ionescu", "1975");
familyName("Popescu", "1978");
familyName("Zinescu", "1983");
?>
PHP este un limbaj tiparit mai puțin (PHP is a Loosely Typed Language)
În exemplul precedent, observați că nu trebuie să spunem PHP-ului ce tip de date (data type) este variabila.
PHP asociază automat un tip de date (data type) variabilei, în funcție de valoarea acesteia. Deoarece tipurile de date (data types) nu sunt setate într-un sens strict, puteți face lucruri precum adăugarea unui șir (string) la un număr întreg (integer) fără a provoca o eroare.
În PHP 7, au fost adăugate declarații de tip (type declarations). Aceasta ne oferă opțiunea de a specifica tipul de date (data type) preconizat la declararea unei funcții, iar prin adăugarea declarației strict, va arunca o „Fatal Error” dacă nu există o nepotrivire a tipului de date (data type).
În exemplul următor, încercăm să trimitem atât un număr cât și un șir (string) la funcție fără a folosi o declarația strict:
<?php
function addNumbers(int $a, int $b) {
return $a + $b;
}
echo addNumbers(5, "5 days");
// deoarece NU este activat strict, „5 days” este schimbat în int(5) și va întoarce 10
?>
Pentru a specifica strict trebuie să setăm declarația (strict_types=1);. Aceasta trebuie să fie chiar în prima linie a fișierului PHP.
În exemplul următor încercăm să trimitem atât un număr cât și un șir (string) la funcție, dar aici am adăugat declarația strict:
<?php declare(strict_types=1); // cerință strictă
function addNumbers(int $a, int $b) {
return $a + $b;
}
echo addNumbers(5, "5 days");
// din moment ce strict este activat și „5 days” nu este un număr întreg (integer), va fi afișată o eroare
?>
PHP valoarea argumentului default (PHP Default Argument Value)
Următorul exemplu arată cum se utilizează un parametru default (parametru impicit). Dacă numim funcția setHeight() fără argumente, aceasta are valoarea default (valoarea implicită) ca argument:
<?php declare(strict_types=1); // strict requirement
function setHeight(int $minheight = 50) {
echo "Înălțimea este: $minheight <br>";
}
setHeight(350);
setHeight(); // vom folosi valoarea default (valoarea implicită) of 50
setHeight(135);
setHeight(80);
?>
Funcții PHP - Returnarea valorilor
Pentru a permite unei funcții să returneze o valoare, utilizați instrucțiunea return:
<?php declare(strict_types=1); // cerință strictă
function sum(int $x, int $y) {
$z = $x + $y;
return $z;
}
echo "5 + 10 = " . sum(5, 10) . "<br>";
echo "7 + 13 = " . sum(7, 13) . "<br>";
echo "2 + 4 = " . sum(2, 4);
?>
PHP Declarații de tip return (PHP Return Type Declarations)
PHP 7 acceptă, de asemenea, declarații de tip (Type Declarations) pentru instrucțiunea return. Ca și în cazul declarației de tip (type declaration) pentru argumentele funcției, activând cerința strictă, va returna o „Fatal Error” ca nepotrivire de tip (type mismatch).
Pentru a declara un tip (type) pentru funcția returnată, adăugați două puncte (:) și tipul (type) chiar înainte de paranteza ondulată de deschidere ({) la declararea funcției.
În următorul exemplu, specificăm tipul return (return type) pentru funcție:
<?php declare(strict_types=1); // cerință strictă
function addNumbers(float $a, float $b) : float {
return $a + $b;
}
echo addNumbers(1.2, 5.2);
?>
Puteți specifica un tip de returnare (return type) diferit de cel al argumentelor, dar asigurați-vă că returnarea este cea corectă:
<?php declare(strict_types=1); // cerință strictă
function addNumbers(float $a, float $b) : int {
return (int)($a + $b);
}
echo addNumbers(1.2, 5.2);
?>
PHP Array
Un array (tablou) stochează mai multe valori într-o singură variabilă:
<?php
$cars = array("Volvo", "BMW", "Toyota");
echo "Îmi place " . $cars[0] . ", " . $cars[1] . " and " . $cars[2] . ".";
?>
Ce este un Array?
Un array (tablo) este o variabilă specială, care poate reține mai mult de o valoare simultan.
Dacă aveți o listă de articole (de exemplu, o listă cu nume de mașini), stocarea mașinilor în variabile unice ar putea arăta astfel:
$cars1 = "Volvo";
$cars2 = "BMW";
$cars3 = "Toyota";
Cu toate acestea, ce se întâmplă dacă doriți să vă buclați (loop) între mașini și să găsiți una specifică? Și dacă nu ai avea 3 mașini, ci 300?
Soluția este să creezi un array (tablou)!
Un array (tablou) poate reține multe valori sub un singur nume și puteți accesa valorile făcând referire la un număr de index.
Creați un array (o matrice) în PHP
În PHP, funcția array() este utilizată pentru a crea un tablou (array):
array ();
În PHP, există trei tipuri de matrice:
Matrice indexate (Indexed arrays) - Arrays cu un index numeric
Matrice asociative (Associative arrays) - Arrays cu chei (keys) numite
Matricele multidimensionale (Multidimensional arrays) - Arrays care conțin unul sau mai multe tablouri (arrays)
Obțineți Lungimea unui Array - Funcția count()
Funcția count() este utilizată pentru a returna lungimea (numărul de elemente) unui array (tablou):
<?php
$cars = array("Volvo", "BMW", "Toyota");
echo count($cars);
?>
PHP matrice indexate (PHP Indexed Arrays)
Există două moduri de a crea tablouri indexate (indexed arrays):
Indexul poate fi atribuit automat (indexul începe întotdeauna de la 0), astfel:
$cars = array("Volvo", "BMW", "Toyota");
sau indexul poate fi atribuit manual:
$cars[0] = "Volvo";
$cars[1] = "BMW";
$cars[2] = "Toyota";
Următorul exemplu creează un tablou indexat (indexed array) numit $cars, îi atribuie trei elemente și apoi tipărește un text care conține valorile tabloului (array values):
<?php
$cars = array("Volvo", "BMW", "Toyota");
echo "Îmi place " . $cars[0] . ", " . $cars[1] . " and " . $cars[2] . ".";
?>
Buclă printr-o matrice indexată (Loop Through an Indexed Array)
Pentru a parcurge și tipări toate valorile unui tablou indexat (indexed array), puteți utiliza o buclă (loop) for, astfel:
<?php
$cars = array("Volvo", "BMW", "Toyota");
$arrlength = count($cars);
for($x = 0; $x < $arrlength; $x++) {
echo $cars[$x];
echo "<br>";
}
?>
PHP matrice asociative (PHP Associative Arrays)
Matricele asociative (associative arrays) sunt tablouri (arrays) care folosesc chei numite (named keys) pe care le atribuiți lor.
Există două moduri de a crea un tablou asociativ (associative array):
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
sau:
$age['Petre'] = "35";
$age['Ion'] = "37";
$age['Dan'] = "43";
Cheile denumite (named keys) pot fi apoi utilizate într-un script:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
echo "Petre are " . $age['Petre'] . " ani.";
?>
Buclă printr-o matrice asociativă (Loop Through an Associative Array)
Pentru a parcurge și tipări toate valorile unui tablou asociativ (associative array), puteți utiliza o buclă (loop) foreach, astfel:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
foreach($age as $x => $x_value) {
echo "Key=" . $x . ", Value=" . $x_value;
echo "<br>";
}
?>
PHP matrice multidimensionale (PHP Multidimensional Arrays)
În paginile anterioare, am descris matricile (arrays) care reprezintă o listă unică de perechi cheie/valoare (key/value).
Cu toate acestea, uneori doriți să stocați valorile cu mai mult de o cheie. Pentru aceasta, avem tablouri multidimensionale (multidimensional arrays).
PHP - Arrayuri multidimensionale
Un tablou multidimensional (multidimensional array) este un tablou (array) care conține unul sau mai multe tablouri (arrays).
PHP acceptă tablouri multidimensionale (multidimensional arrays) care sunt la două, trei, patru, cinci sau mai multe niveluri. Cu toate acestea, tablourile (arrays) cu mai mult de trei niveluri sunt greu de gestionat pentru majoritatea oamenilor.
Dimensiunea unui tablou (array) indică numărul de indici de care aveți nevoie pentru a selecta un element.
Pentru un tablou bidimensional (two-dimensional array), aveți nevoie de doi indici pentru a selecta un element
Pentru un tablou tridimensional (three-dimensional array), aveți nevoie de trei indici pentru a selecta un elementPHP - Matricele bidimensionale (PHP - Two-dimensional Arrays)
Un tablou bidimensional (two-dimensional array) este un tablou de matrice (array of arrays) (un tablou tridimensional (three-dimensional array) este un tablou de tablouri (arrays of arrays)).
Putem stoca datele dintr-un tabel într-un tablou bidimensional (two-dimensional array), astfel:
$cars = array
(
array("Volvo",22,18),
array("BMW",15,13),
array("Saab",5,2),
array("Land Rover",17,15)
);
Acum, two-dimensional $cars array conține patru tablouri (arrays) și are doi indici: rând și coloană (row and column).
Pentru a avea acces la elementele tabloului (array) $cars trebuie să indicăm cei doi indici (rând și coloană/row and column):
<?php
echo $cars[0][0].": În stoc: ".$cars[0][1].", sold: ".$cars[0][2].".<br>";
echo $cars[1][0].": În stoc: ".$cars[1][1].", sold: ".$cars[1][2].".<br>";
echo $cars[2][0].": În stoc: ".$cars[2][1].", sold: ".$cars[2][2].".<br>";
echo $cars[3][0].": În stoc: ".$cars[3][1].", sold: ".$cars[3][2].".<br>";
?>
<?php
for ($row = 0; $row < 4; $row++) {
echo "<p><b>Numărul rândului $row</b></p>";
echo "<ul>";
for ($col = 0; $col < 3; $col++) {
echo "<li>".$cars[$row][$col]."</li>";
}
echo "</ul>";
}
?>
PHP matrice de sortare. (PHP Sorting Arrays)
Elementele dintr-un tablou (array) pot fi sortate în ordine alfabetică sau numerică, descrescător sau crescător.
PHP - Funcții de sortare pentru matrice (PHP - Sort Functions For Arrays)
În acest capitol, vom parcurge următoarele funcții de sortare a tablelor (arrays) PHP:
sort() - sortează tablourile (arrays) în ordine crescătoare.
rsort() - sortează tablourile (arrays) în ordine descrescătoare.
asort() - sortează tablourile asociative (associative arrays) în ordine crescătoare, în funcție de valoare.
ksort() - sortează matricile asociative (associative arrays) în ordine crescătoare, în funcție de cheie.
arsort() - sortează tablourile asociative (associative arrays) în ordine descrescătoare, în funcție de valoare.
krsort() - sortează tablourile asociative (associative arrays) în ordine descrescătoare, în funcție de cheie.
Sortare Array în ordine crescătoare - sort()
Următorul exemplu sortează elementele tabloului (array) $cars în ordine alfabetică ascendentă:
<?php
$cars = array("Volvo", "BMW", "Toyota");
sort($cars);
?>
Următorul exemplu sortează elementele tabloului (array) $numbers în ordine numerică crescătoare:
<?php
$numbers = array(4, 6, 2, 22, 11);
sort($numbers);
?>
Sortare Array în ordine descrescătoare - rsort()
Următorul exemplu sortează elementele tabloului (array) $cars în ordine alfabetică descrescătoare:
<?php
$cars = array("Volvo", "BMW", "Toyota");
rsort($cars);
?>
Următorul exemplu sortează elementele tabloului (array) $numbers în ordine numerică descrescătoare:
<?php
$numbers = array(4, 6, 2, 22, 11);
rsort($numbers);
?>
Sortare Array (ordine crescătoare), în funcție de valoarea - asort()
Următorul exemplu sortează un tablou asociativ (associative array) în ordine crescătoare, în funcție de valoare:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
asort($age);
?>
Sortare Array (ordine crescătoare), în funcție de cheia - ksort()
Următorul exemplu sortează un tablou asociativ (associative array) în ordine crescătoare, în funcție de cheie:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
ksort($age);
?>
Sortare Array (ordine descrescătoare), în funcție de valoarea - arsort()
Următorul exemplu sortează un tablou asociativ (associative array) în ordine descrescătoare, în funcție de valoare:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
arsort($age);
?>
Sortare Array (ordine descrescătoare), în funcție de cheia - krsort()
Următorul exemplu sortează un tablou asociativ (associative array) în ordine descrescătoare, în funcție de cheie:
<?php
$age = array("Petre"=>"35", "Ion"=>"37", "Dan"=>"43");
krsort($age);
?>
PHP Variabile Globale - Superglobale
PHP Variabile Globale - Superglobalele
Superglobalele au fost introduse în PHP 4.1.0 și sunt variabile încorporate (built-in variables) care sunt întotdeauna disponibile în toate domeniile.
PHP Variabile Globale - Superglobalele
Unele variabile predefinite din PHP sunt „superglobale”, ceea ce înseamnă că sunt întotdeauna accesibile, indiferent de sfera de acțiune - și le puteți accesa din orice funcție, clasă sau fișier fără a fi nevoie să faceți nimic special.
Variabilele superglobale PHP sunt: $GLOBALS, $_SERVER, $_REQUEST, $_POST, $_GET, $_FILES, $_ENV, $_COOKIE, $_SESSION.
Capitolele următoare vor explica unele dintre superglobale, iar restul va fi explicat în capitolele ulterioare.
PHP Superglobal - $GLOBALS
Variabilele super globale sunt variabile încorporate (built-in variables), care sunt întotdeauna disponibile în toate domeniile.
PHP $GLOBALS
$GLOBALS este o variabilă super globală PHP, care este utilizată pentru a accesa variabile globale de oriunde în scriptul PHP (de asemenea, din funcții sau metode).
PHP stochează toate variabilele globale într-un tablou numit $GLOBALS [index]. Indicele conține numele variabilei.
Exemplul de mai jos arată cum se utilizează variabila super globală $GLOBALS:
<?php
$x = 75;
$y = 25;
function addition() {
$GLOBALS['z'] = $GLOBALS['x'] + $GLOBALS['y'];
}
addition();
echo $z;
?>
În exemplul de mai sus, deoarece z este o variabilă prezentă în matricea (array) $GLOBALS, este accesibilă și din afara funcției!
PHP Superglobal - $_SERVER
Variabilele super globale sunt variabile încorporate (built-in variables), care sunt întotdeauna disponibile în toate domeniile.
PHP $ _SERVER
$ _SERVER este o variabilă super globală PHP care conține informații despre antetele, căile și locațiile scriptului (headers, paths, and script locations).
Exemplul de mai jos arată cum să folosiți unele dintre elementele din $ _SERVER:
<?php
echo $_SERVER['PHP_SELF'];
echo "<br>";
echo $_SERVER['SERVER_NAME'];
echo "<br>";
echo $_SERVER['HTTP_HOST'];
echo "<br>";
echo $_SERVER['HTTP_REFERER'];
echo "<br>";
echo $_SERVER['HTTP_USER_AGENT'];
echo "<br>";
echo $_SERVER['SCRIPT_NAME'];
?>
Următorul tabel prezintă cele mai importante elemente care pot intra în interiorul $ _SERVER:
$ _SERVER ['PHP_SELF'] Returnează numele de fișier al scriptului care se execută în prezent
$ _SERVER ['GATEWAY_INTERFACE'] Returnează versiunea Interfaței de Gateway comun (CGI) pe care serverul o folosește
$ _SERVER ['SERVER_ADDR'] Returnează adresa IP a serverului gazdă
$ _SERVER ['SERVER_NAME'] returnează numele serverului gazdă (cum ar fi www.w3schools.com)
$ _SERVER ['SERVER_SOFTWARE'] returnează șirul de identificare a serverului (cum ar fi Apache / 2.2.24)
$ _SERVER ['SERVER_PROTOCOL'] returnează numele și revizuirea protocolului informațional (cum ar fi HTTP / 1.1)
$ _SERVER ['REQUEST_METHOD'] returnează metoda de solicitare folosită pentru a accesa pagina (cum ar fi POST)
$ _SERVER ['REQUEST_TIME'] returnează intervalul de timp al începerii cererii (cum ar fi 1377687496)
$ _SERVER ['QUERY_STRING'] Returnează șirul de interogare dacă pagina este accesată printr-un șir de interogare
$ _SERVER ['HTTP_ACCEPT'] Returnează antetul Accept din cererea curentă
$ _SERVER ['HTTP_ACCEPT_CHARSET'] returnează antetul Accept_Charset din cererea curentă (cum ar fi utf-8, ISO-8859-1)
$ _SERVER ['HTTP_HOST'] Returnează antetul gazdei din cererea curentă
$ _SERVER ['HTTP_REFERER'] returnează adresa URL completă a paginii curente (nu este de încredere, deoarece nu toți agenții utilizator o acceptă)
$ _SERVER ['HTTPS'] Este scriptul cerut printr-un protocol HTTP sigur
$ _SERVER ['REMOTE_ADDR'] Returnează adresa IP de unde utilizatorul vizualizează pagina curentă
$ _SERVER ['REMOTE_HOST'] returnează numele gazdei de unde utilizatorul vizualizează pagina curentă
$ _SERVER ['REMOTE_PORT'] Returnează portul utilizat pe mașina utilizatorului pentru a comunica cu serverul web
$ _SERVER ['SCRIPT_FILENAME'] Returnează numele de cale absolut al scriptului care se execută în prezent
$ _SERVER ['SERVER_ADMIN'] Returnează valoarea acordată directivei SERVER_ADMIN din fișierul de configurare a serverului web (dacă scriptul rulează pe o gazdă virtuală, va fi valoarea definită pentru acea gazdă virtuală) (cum ar fi [email protected] )
$ _SERVER ['SERVER_PORT'] Returnează portul pe mașina serverului care este utilizat de serverul web pentru comunicare (cum ar fi 80)
$ _SERVER ['SERVER_SIGNATURE'] Returnează versiunea serverului și numele gazdei virtuale care sunt adăugate la paginile generate de server
$ _SERVER ['PATH_TRANSLATED'] returnează calea bazată pe sistemul de fișiere la scriptul curent
$ _SERVER ['SCRIPT_NAME'] returnează calea scriptului curent
$ _SERVER ['SCRIPT_URI'] Returnează URI-ul paginii curente
PHP Superglobal - $_REQUEST
Variabilele super globale sunt variabile încorporate (built-in variables), care sunt întotdeauna disponibile în toate domeniile.
PHP $ _REQUEST
PHP $ _REQUEST este o variabilă super globală PHP care este folosită pentru a colecta date după trimiterea unui formular HTML.
Exemplul de mai jos arată un formular cu un câmp de intrare și un buton de trimitere (input field și submit button). Când un utilizator trimite datele făcând click pe „Trimite” (Submit), datele formularului sunt trimise fișierului specificat în atributul de acțiune (action attribute) al etichetei (tag) <form>. În acest exemplu, indicăm acest fișier în sine pentru prelucrarea datelor din formular. Dacă doriți să utilizați un alt fișier PHP pentru procesarea datelor din formular, înlocuiți-l cu numele de fișier ales. Apoi, putem folosi super variabila globală $ _REQUEST pentru a colecta valoarea câmpului de intrare (input field):
<html>
<body>
<form method="post" action="<?php echo $_SERVER['PHP_SELF'];?>">
Nume: <input type="text" name="fname">
<input type="submit">
</form>
<?php
if ($_SERVER["REQUEST_METHOD"] == "POST") {
// colectați valoarea câmpului de intrare (input field)
$name = $_REQUEST['fname'];
if (empty($name)) {
echo "Numele este gol";
} else {
echo $name;
}
}
?>
</body>
</html>
PHP Superglobal - $_POST
Variabilele super globale sunt variabile încorporate (built-in variables), care sunt întotdeauna disponibile în toate domeniile.
PHP $ _POST
PHP $ _POST este o variabilă super globală PHP, care este folosită pentru a colecta date de formular după trimiterea unui formular HTML cu method="post".
$ _POST este de asemenea utilizat pe scară largă pentru a trece variabilele.
Exemplul de mai jos arată un formular cu un câmp de intrare și un buton de trimitere (input field și submit button). Când un utilizator trimite datele făcând click pe „Trimite” (Submit), datele formularului sunt trimise fișierului specificat în atributul de acțiune (action attribute) al etichetei (tag) <form>. În acest exemplu, indicăm fișierul în sine pentru prelucrarea datelor din formular. Dacă doriți să utilizați un alt fișier PHP pentru procesarea datelor din formular, înlocuiți-l cu numele de fișier ales. Apoi, putem utiliza super variabila globală $ _POST pentru a colecta valoarea câmpului de intrare (input field):
<html>
<body>
<form method="post" action="<?php echo $_SERVER['PHP_SELF'];?>">
Nume: <input type="text" name="fname">
<input type="submit">
</form>
<?php
if ($_SERVER["REQUEST_METHOD"] == "POST") {
// colectați valoarea câmpului de intrare (input field)
$name = $_POST['fname'];
if (empty($name)) {
echo "Numele este gol";
} else {
echo $name;
}
}
?>
</body>
</html>
PHP Superglobal - $_GET
Variabilele super globale sunt variabile încorporate (built-in variables), care sunt întotdeauna disponibile în toate domeniile.
PHP $ _GET
PHP $ _GET este o variabilă super globală PHP, care este utilizată pentru a colecta date de formular după trimiterea unui formular HTML cu method="get".
$ _GET poate colecta și datele trimise pe adresa URL.
Presupunem că avem o pagină HTML care conține un hyperlink cu parametri:
<html>
<body>
<a href="test_get.php?subject=PHP&web=lectii-virtuale.ro">Test $GET</a>
</body>
</html>
Când un utilizator face click pe linkul „Test $GET”, parametrii „subject” și „web” sunt trimiși la „test_get.php”, iar apoi puteți accesa valorile sale în „test_get.php” cu $_GET.
Exemplul de mai jos arată codul din „test_get.php”:
<html>
<body>
<?php
echo "Studiu " . $_GET['subject'] . " la " . $_GET['web'];
?>
</body>
</html>
PHP Manipularea formularelor
PHP Form Handling
Superglobalele PHP $_GET și $_POST sunt utilizate pentru colectarea datelor de formular.
PHP - Un formular HTML simplu
Exemplul de mai jos afișează un formular HTML simplu cu două câmpuri de introducere și un buton de trimitere (input fields și submit button):
<html>
<body>
<form action="welcome.php" method="post">
Nume: <input type="text" name="name"><br>
E-mail: <input type="text" name="email"><br>
<input type="submit">
</form>
</body>
</html>
Când utilizatorul completează formularul de mai sus și face click pe butonul de trimitere (submit), datele formularului sunt trimise pentru procesare într-un fișier PHP numit „welcome.php”. Datele formularului sunt trimise cu metoda HTTP POST.
Pentru a afișa datele trimise, pur și simplu puteți echo toate variabilele. „Welcome.php” arată astfel:
<html>
<body>
Bun venit <?php echo $_POST["name"]; ?><br>
Adresa dvs. de e-mail este: <?php echo $_POST["email"]; ?>
</body>
</html>
Rezultatul ar putea fi ceva de genul:
Bun venit Ion
Adresa dvs. de e-mail este [email protected]
Același rezultat ar putea fi obținut și folosind metoda HTTP GET:
<html>
<body>
<form action="welcome_get.php" method="get">
Nume: <input type="text" name="name"><br>
E-mail: <input type="text" name="email"><br>
<input type="submit">
</form>
</body>
</html>
și „welcome_get.php” arată astfel:
<html>
<body>
Bun venit <?php echo $_GET["name"]; ?><br>
Adresa dvs. de e-mail este: <?php echo $_GET["email"]; ?>
</body>
</html>
Codul de mai sus este destul de simplu. Cu toate acestea, cel mai important lucru lipsește. Trebuie să validați datele formularului pentru a vă proteja scriptul împotriva codului rău intenționat.
Gândiți-vă la SECURITATE când prelucrați formularele PHP!
Această pagină nu conține nicio validare a formularului, ci doar arată cum puteți trimite și recupera datele de formular.
Cu toate acestea, paginile următoare vor arăta cum să procesați formularele PHP cu securitate în minte! Validarea corectă a datelor formularului este importantă pentru a vă proteja formularul de hackeri și spameri!
GET vs. POST
Atât GET, cât și POST creează un tablou (array) (de exemplu, array( key1 => value1, key2 => value2, key3 => value3, ...)). Acest tablou (array) conține perechi cheie/valoare (key/value), unde cheile (keys) sunt numele controalelor de formular (form controls) și valorile sunt datele de intrare (input data) de la utilizator.
Atât GET, cât și POST sunt tratate ca $_GET și $_POST. Acestea sunt superglobale, ceea ce înseamnă că sunt întotdeauna accesibile, indiferent de sfera de aplicare - și le puteți accesa din orice funcție, clasă sau fișier (function, class or file) fără a fi nevoie să faceți nimic special.
$_GET reprezintă o serie de variabile transmise scriptului curent prin parametrii URL.
$ _POST reprezintă o serie de variabile transmise scriptului curent prin metoda HTTP POST.
Când să folosiți GET?
Informațiile trimise dintr-un formular cu metoda GET sunt vizibile tuturor (toate numele variabilelor și valorile (variable names/ values) sunt afișate pe adresa URL). GET are, de asemenea, limite privind cantitatea de informații care trebuie trimise. Limitarea este de aproximativ 2000 de caractere. Cu toate acestea, deoarece variabilele sunt afișate în adresa URL, este posibilă marcarea paginii. Acest lucru poate fi util în unele cazuri.
GET poate fi utilizat pentru trimiterea de date non-sensibile (non-sensitive data).
GET nu ar trebui niciodată utilizat pentru trimiterea de parole sau alte informații sensibile!
Când să folosiți POST?
Informațiile trimise dintr-un formular cu metoda POST sunt invizibile pentru alții (toate numele/valorile (names/values) sunt încorporate în corpul solicitării (body) HTTP) și nu au limite privind cantitatea de informații de trimis.
Mai mult, POST acceptă funcționalități avansate, cum ar fi asistența pentru intrarea binară în mai multe părți (multi-part binary input) în timp ce încărcați fișiere pe server.
Cu toate acestea, deoarece variabilele nu sunt afișate în adresa URL, nu este posibilă marcarea paginii.
Dezvoltatorii preferă POST pentru trimiterea datelor de formular (form data).
PHP Validare formular
Validare formular PHP
Acesta și capitolele următoare arată cum să folosești PHP pentru a valida datele formularului.
Validare formular PHP
Gândiți-vă la SECURITATE când prelucrați formularele PHP!
Aceste pagini vor arăta cum să procesați formularele PHP din punct de vedere al securitatii. Validarea corectă a datelor din formular este importantă pentru a vă proteja formularul de hackeri și spameri!
Formularul HTML la care vom lucra în aceste capitole, conține diferite câmpuri de introducere: câmpuri de text obligatorii și opționale, butoane radio și un buton de trimitere (required and optional text fields, radio buttons, and a submit button):
Name - Obligatoriu. + Trebuie să conțină doar litere și spațiu alb
E-mail - Obligatoriu. + Trebuie să conțină o adresă de e-mail validă (cu @ și.)
Website - Obligatoriu. Dacă este prezent, trebuie să conțină o adresă URL validă
Comment - Opțional. Câmp de introducere pe mai multe linii (textarea)
Sex - Obligatoriu. Trebuie să selectați una
Mai întâi vom analiza codul HTML simplu pentru formular:
Câmpuri text (Text Fields)
Câmpurile nume, e-mail și website sunt elemente de introducere ale textului (input elements), iar câmpul de comentarii este textarea. Codul HTML arată astfel:
Nume: <input type="text" name="name">
E-mail: <input type="text" name="email">
Website: <input type="text" name="website">
Comment: <textarea name="comment" rows="5" cols="40"></textarea>
Butoane radio (Radio Buttons)
Câmpurile gen (gender fields) sunt butoane radio, iar codul HTML arată astfel:
Gen:
<input type="radio" name="gender" value="female">Femeie
<input type="radio" name="gender" value="male">Bărbat
<input type="radio" name="gender" value="other">Altele
Elementul form (The Form Element)
Codul HTML al formularului arată astfel:
<form method="post" action="<?php echo htmlspecialchars($_SERVER["PHP_SELF"]);?>">
Când formularul este trimis, datele formularului sunt trimise cu method = "post".
Ce este variabila $_SERVER["PHP_SELF"] ?
$_SERVER["PHP_SELF"] este o variabilă super globală care returnează numele de fișier al scriptului care se execută în prezent.
Așadar, $_SERVER["PHP_SELF"] trimite datele formularului (submitted form data) trimis către pagina în sine, în loc să sară pe o altă pagină. În acest fel, utilizatorul va primi mesaje de eroare pe aceeași pagină ca și formularul.
Ce este funcția htmlspecialchars()?
Funcția htmlspecialchars() convertește caracterele speciale în entități HTML. Aceasta înseamnă că va înlocui caractere HTML precum <and> cu < și >. Acest lucru împiedică atacatorii să exploateze codul prin injectarea codului HTML sau a javascriptului (Cross-site Scripting attacks) în formulare.
Notă imporantă privind securitatea formularului PHP
Variabila $_SERVER["PHP_SELF"] poate fi utilizată de hackeri!
Dacă PHP_SELF este utilizat în pagina dvs., un utilizator poate introduce un slash (/) și apoi unele comenzi de Cross Site Scripting (XSS) pentru a executa.
Scripturi încrucișate (Cross-site scripting) (XSS) este un tip de vulnerabilitate a securității computerului care se găsește de obicei în aplicațiile Web. XSS le permite atacatorilor să injecteze scripturi din partea clientului în paginile Web vizualizate de alți utilizatori.
Presupunem că avem următorul formular într-o pagină numită "test_form.php":
<form method="post" action="<?php echo $_SERVER["PHP_SELF"];?>">
Acum, dacă un utilizator introduce URL-ul normal în bara de adrese precum "http://www.example.com/test_form.php", codul de mai sus va fi tradus în:
<form method="post" action="test_form.php">
Până acum, bine.
Cu toate acestea, considerați că un utilizator introduce următoarea adresă URL în bara de adrese:
http://www.example.com/test_form.php/%22%3E%3Cscript%3Ealert('hacked')%3C/script%3E
În acest caz, codul de mai sus va fi tradus în:
<form method="post" action="test_form.php/"><script>alert('hacked')</script>
Acest cod adaugă o etichetă script (script tag) și o comandă de alertă (alert command). Și atunci când pagina se încarcă, codul JavaScript va fi executat (utilizatorul va vedea o casetă de alertă (alert box)). Acesta este doar un exemplu simplu și inofensiv cum poate fi exploatată variabila PHP_SELF.
Fiți conștienți de faptul că orice cod JavaScript poate fi adăugat în eticheta <script>! Un hacker poate redirecționa utilizatorul către un fișier de pe alt server, iar respectivul fișier poate conține cod rău intenționat care poate modifica variabilele globale sau poate trimite formularul la o altă adresă pentru a salva datele utilizatorului, de exemplu.
Cum să evitați exploatările $_SERVER["PHP_SELF"]?
Exploatările $_SERVER["PHP_SELF"] pot fi evitate folosind funcția htmlspecialchars().
Codul formularului ar trebui să arate astfel:
<form method="post" action="<?php echo htmlspecialchars($_SERVER["PHP_SELF"]);?>">
Funcția htmlspecialchars() convertește caracterele speciale în entități HTML. Acum, dacă utilizatorul încearcă să exploateze variabila PHP_SELF, va rezulta următoarea ieșire (output):
<form method="post" action="test_form.php/"><script>alert('hacked')</script>">
Validați datele formularului cu PHP
Primul lucru pe care îl vom face este să trecem toate variabilele prin funcția PHP htmlspecialchars().
Când folosim funcția htmlspecialchars(); atunci dacă un utilizator încearcă să trimită următoarele într-un câmp text:
<script>location.href('http://www.hacked.com')</script>
- acest lucru nu ar fi executat, deoarece va fi salvat ca și cod HTML scăpat, astfel:
<script>location.href('http://www.hacked.com')</script>
Codul este acum sigur pentru a fi afișat pe o pagină sau în interiorul unui e-mail.
De asemenea, vom face alte două lucruri atunci când utilizatorul va trimite formularul:
Scoateți caracterele inutile (spațiu suplimentar, filă, linie nouă (extra space, tab, newline)) din datele de intrare ale utilizatorului (cu funcția PHP trim() )
Eliminați backslashes (\) din datele de intrare ale utilizatorului (cu funcția PHP stripslashes())Următorul pas este să creem o funcție care să facă toate verificările pentru noi (ceea ce este mult mai convenabil decât scrierea aceluiași cod încă o dată).
Vom numi funcția test_input().
Acum, putem verifica fiecare variabilă $_POST cu funcția test_input(), iar scriptul va arata astfel:
<?php
// definiți variabilele și setați valorile goale
$name = $email = $gender = $comment = $website = "";
if ($_SERVER["REQUEST_METHOD"] == "POST") {
$name = test_input($_POST["name"]);
$email = test_input($_POST["email"]);
$website = test_input($_POST["website"]);
$comment = test_input($_POST["comment"]);
$gender = test_input($_POST["gender"]);
}
function test_input($data) {
$data = trim($data);
$data = stripslashes($data);
$data = htmlspecialchars($data);
return $data;
}
?>
Observați că la începutul scriptului, verificăm dacă formularul a fost trimis folosind $_SERVER ["REQUEST_METHOD"]. Dacă REQUEST_METHOD este POST, atunci formularul a fost trimis - și ar trebui validat. Dacă nu a fost trimis, săriți validarea și afișați un formular necompletat.
Cu toate acestea, în exemplul de mai sus, toate câmpurile de introducere sunt opționale. Scriptul funcționează bine chiar dacă utilizatorul nu introduce date.
Următorul pas este de a face necesare câmpurile de intrare și de a crea mesaje de eroare, dacă este nevoie.
PHP Formular Obligatoriu
Formulare PHP - Câmpuri obligatorii (PHP Forms - Required Fields)
Acest capitol arată cum se pot face câmpurile de intrare necesare (input fields required) și se pot crea mesaje de eroare (error messages), dacă este nevoie.
PHP - Câmpuri obligatorii (PHP - Required Fields)
Din tabelul cu regulile de validare din pagina anterioară, vedem că sunt obligatorii câmpurile „Nume”, „E-mail” și „Gen”. Aceste câmpuri nu pot fi goale și trebuie completate în formularul HTML.
Nume- Obligatoriu. Trebuie să conțină doar litere și spațiu alb.
E-mail - Obligatoriu. Trebuie să conțină o adresă de e-mail validă (cu @ și.).
Website - Opțional. Dacă este prezent, trebuie să conțină o adresă URL validă.
Comentariu - Opțional. Câmp de introducere pe mai multe linii (textarea).
Gen - Obligatoriu. Trebuie să selectați unul.
În capitolul precedent, toate câmpurile de intrare (input fields) au fost opționale.
În codul următor, am adăugat câteva variabile noi: $nameErr, $emailErr, $genderErr și $websiteErr $. Aceste variabile de eroare (error variables) vor conține mesaje de eroare (error messages) pentru câmpurile necesare (required fields). Am adăugat, de asemenea, o instrucțiune if else pentru fiecare variabilă $_POST. Se verifică dacă variabila $_POST este goală (cu funcția PHP empty()). Dacă este gol, un mesaj de eroare (error message) este stocat în diferite variabile de eroare (error variables) și, dacă nu este gol, trimite datele de intrare (input data) ale utilizatorului prin funcția test_input():
<?php
// definiți variabilele și setați valorile goale
$nameErr = $emailErr = $genderErr = $websiteErr = "";
$name = $email = $gender = $comment = $website = "";
if ($_SERVER["REQUEST_METHOD"] == "POST") {
if (empty($_POST["name"])) {
$nameErr = "Name is required";
} else {
$name = test_input($_POST["name"]);
}
if (empty($_POST["email"])) {
$emailErr = "Email is required";
} else {
$email = test_input($_POST["email"]);
}
if (empty($_POST["website"])) {
$website = "";
} else {
$website = test_input($_POST["website"]);
}
if (empty($_POST["comment"])) {
$comment = "";
} else {
$comment = test_input($_POST["comment"]);
}
if (empty($_POST["gender"])) {
$genderErr = "Gender is required";
} else {
$gender = test_input($_POST["gender"]);
}
}
?>
PHP - Afișează mesajele de eroare (PHP - Display The Error Messages)
Apoi, în formularul HTML, adăugăm putin de script după fiecare câmp necesar (required field), care generează mesajul de eroare (error message) corect dacă este necesar (adică dacă utilizatorul încearcă să trimită formularul fără a completa câmpurile necesare (required fields)):
<form method="post" action="<?php echo htmlspecialchars($_SERVER["PHP_SELF"]);?>">
Nume: <input type="text" name="name">
<span class="error">* <?php echo $nameErr;?></span>
<br><br>
E-mail:
<input type="text" name="email">
<span class="error">* <?php echo $emailErr;?></span>
<br><br>
Website:
<input type="text" name="website">
<span class="error"><?php echo $websiteErr;?></span>
<br><br>
Coment: <textarea name="comment" rows="5" cols="40"></textarea>
<br><br>
Gen:
<input type="radio" name="gender" value="female">Female
<input type="radio" name="gender" value="male">Male
<input type="radio" name="gender" value="other">Other
<span class="error">* <?php echo $genderErr;?></span>
<br><br>
<input type="submit" name="submit" value="Submit">
</form>
Următorul pas este validarea datelor de intrare (input data), adică „Conține câmpul Nume doar litere și spațiu alb?”, iar „Conține câmpul E-mail o sintaxă a adresei de e-mail validă?”, iar dacă este completat, ”Conține câmpul Website o adresă URL validă? ".
PHP Formular - E-mail/URL
Formulare PHP - Validați e-mailul și adresa URL
Acest capitol arată cum se pot valida numele, e-mailurile și adresele URL.
PHP - Validare nume
Codul de mai jos arată o modalitate simplă de a verifica dacă câmpul de nume conține doar litere și spațiu alb. Dacă valoarea câmpului nume nu este validă, atunci stocați un mesaj de eroare:
$name = test_input($_POST["name"]);
if (!preg_match("/^[a-zA-Z ]*$/",$name)) {
$nameErr = "Sunt permise doar litere și spațiu alb";
}
Funcția preg_match() caută un șir de șablon (string for pattern), returnând adevărat (true) dacă modelul (pattern) există și fals (false) altfel.
PHP - Validare e-mail
Cel mai simplu și mai sigur mod de a verifica dacă o adresă de e-mail este bine formulată este să folosești funcția PHP filter_var().
În codul de mai jos, dacă adresa de e-mail nu este bine formulată, atunci stocați un mesaj de eroare (error message):
$email = test_input($_POST["email"]);
if (!filter_var($email, FILTER_VALIDATE_EMAIL)) {
$emailErr = "Format de e-mail invalid";
}
PHP - Validare URL
Codul de mai jos arată o modalitate de a verifica dacă o sintaxă a adresei URL este validă (această expresie obișnuită permite și liniuțe în adresa URL). Dacă sintaxa adresei URL nu este validă, atunci stocați un mesaj de eroare (error message):
$website = test_input($_POST["website"]);
if (!preg_match("/\b(?:(?:https?|ftp):\/\/|www\.)[-a-z0-9+&@#\/%?=~_|!:,.;]*[-a-z0-9+&@#\/%=~_|]/i",$website)) {
$websiteErr = "URL invalid";
}
PHP - Validați numele, e-mailul și adresa URL
Scriptul acum arată așa:
<?php
// definiți variabilele și setați valorile goale
$nameErr = $emailErr = $genderErr = $websiteErr = "";
$name = $email = $gender = $comment = $website = "";
if ($_SERVER["REQUEST_METHOD"] == "POST") {
if (empty($_POST["name"])) {
$nameErr = "Numele este necesar";
} else {
$name = test_input($_POST["name"]);
// verificați dacă numele conține doar litere și spațiu alb
if (!preg_match("/^[a-zA-Z ]*$/",$name)) {
$nameErr = "Sunt permise doar litere și spațiu alb";
}
}
if (empty($_POST["email"])) {
$emailErr = "Email is required";
} else {
$email = test_input($_POST["email"]);
// verificați dacă adresa de e-mail este bine formulată
if (!filter_var($email, FILTER_VALIDATE_EMAIL)) {
$emailErr = "Format de e-mail nevalid";
}
}
if (empty($_POST["website"])) {
$website = "";
} else {
$website = test_input($_POST["website"]);
// verificați dacă sintaxa adresei URL este validă (această expresie obișnuită permite și liniuțe în URL)
if (!preg_match("/\b(?:(?:https?|ftp):\/\/|www\.)[-a-z0-9+&@#\/%?=~_|!:,.;]*[-a-z0-9+&@#\/%=~_|]/i",$website)) {
$websiteErr = "URL nevalid";
}
}
if (empty($_POST["comment"])) {
$comment = "";
} else {
$comment = test_input($_POST["comment"]);
}
if (empty($_POST["gender"])) {
$genderErr = "Genul este necesar";
} else {
$gender = test_input($_POST["gender"]);
}
}
?>
Următorul pas este să arătați cum să împiedicați formularul să golească toate câmpurile de intrare (input fields) atunci când utilizatorul trimite formularul.
PHP Formular complet
Exemplu de formular complet PHP (PHP Complete Form Example)
Acest capitol arată cum să păstrați valorile în câmpurile de introducere (input fields) atunci când utilizatorul apasă butonul de trimitere (submit button).
PHP - Păstrați valorile în formular
Pentru a afișa valorile din câmpurile de intrare (input fields) după ce utilizatorul apasă pe butonul de trimitere (submit button), adăugăm puțin script PHP în interiorul valorii atributului (value attribute) al următoarelor câmpuri de intrare (input fields): nume, e-mail și site-ul web (name, email, and website). În câmpul textarea (textarea field) comment, am pus scriptul între etichetele (tags)<textarea> și </textarea>. Micul script produce (outputs) valoarea variabilelor $name, $email, $website și $comment.
Apoi, trebuie să arătăm și ce buton radio (radio button) a fost bifat. Pentru aceasta, trebuie să manipulăm atributul bifat (checked attribute) (nu atributul valoare pentru butoanele radio) (radio buttons):
Nume: <input type="text" name="name" value="<?php echo $name;?>">
E-mail: <input type="text" name="email" value="<?php echo $email;?>">
Website: <input type="text" name="website" value="<?php echo $website;?>">
Comentariu: <textarea name="comment" rows="5" cols="40"><?php echo $comment;?></textarea>
Gen:
<input type="radio" name="gender"
<?php if (isset($gender) && $gender=="female") echo "checked";?>
value="female">Femeie
<input type="radio" name="gender"
<?php if (isset($gender) && $gender=="male") echo "checked";?>
value="male">Bărbat
<input type="radio" name="gender"
<?php if (isset($gender) && $gender=="other") echo "checked";?>
value="other">Altele
PHP Data și Ora
PHP Data și ora (PHP Date and Time)
Funcția PHP date() este utilizată pentru formatarea unei date și/sau a unei ore.
Funcția PHP date()
Funcția PHP date() formatează un marcaj de timp (timestamp) într-o dată și o oră mai lizibile.
Sintaxă
date(format,timestamp)
format - Obligatoriu. Specifică formatul de timp (timestamp)
timestamp - Opțional. Specifică un marcaj de timp (timestamp). Valoarea implicită (default) o reprezintă data și ora curente
Un marcaj de timp (timestamp) este o succesiune de caractere, care indică data și/sau ora la care a avut loc un anumit eveniment.
Obțineți o dată
Parametrul format necesar al funcției date() specifică modul de formatare al datei (sau orei).
Iată câteva caractere care sunt utilizate frecvent pentru date:
d - Reprezintă ziua lunii (01 - 31)
m - Reprezintă o lună (de la 01 la 12)
Y - Reprezintă un an (în patru cifre)
l (lowercase 'L') - Reprezintă ziua săptămânii
Alte caractere, cum ar fi „/”, „.” sau „-” pot fi de asemenea inserate între caractere pentru a adăuga o formatare suplimentară.
Exemplul de mai jos formatează data de astăzi în trei moduri diferite:
<?php
echo "Astăzi este " . date("Y/m/d") . "<br>";
echo "Astăzi este " . date("Y.m.d") . "<br>";
echo "Astăzi este " . date("Y-m-d") . "<br>";
echo "Astăzi este " . date("l");
?>
Obțineți o oră
Iată câteva caractere care sunt utilizate frecvent pentru perioade:
H - format de 24 de ore al unei ore (de la 00 la 23)
h - format de 12 ore al unei ore cu zerouri în față (de la 01 la 12)
i - Minute cu zerouri în față (00-59)
s - Secunde cu zerouri în față (de la 00 la 59)
a - Lowercase Ante meridian și Post meridian (am sau pm)
Exemplul de mai jos emite ora curentă în formatul specificat:
<?php
echo "Ora este " . date("h:i:sa");
?>
Rețineți că funcția PHP date() va returna data/ora curentă a serverului!
Obțineți-vă fusul orar (timezone)
Dacă timpul de întoarcere din cod nu este corect, cel mai probabil este pentru că serverul dvs. se află într-o altă țară sau este configurat pentru un alt fus orar (timezone).
Deci, dacă aveți nevoie de o oră corectă în funcție de o anumită locație, puteți seta fusul orar (timezone) pe care doriți să îl utilizați.
Exemplul de mai jos stabilește fusul orar (timezone) pe „America/New_York”, apoi emite ora curentă în formatul specificat:
<?php
date_default_timezone_set("America/New_York");
echo "Este ora " . date("h:i:sa");
?>
Creați o dată cu mktime()
Parametrul opțional timestamp din funcția date() specifică un marcaj de timp (timestamp). Dacă este omisă, vor fi utilizate data și ora curentă (ca în exemplele de mai sus).
Funcția PHP mktime() întoarce marcajul de timp (timestamp) Unix pentru o dată. Marcajul de timp Unix (timestamp) conține numărul de secunde între Unix Epoch (1 ianuarie 1970 00:00:00 GMT) și ora specificată.
Sintaxă
mktime(hour, minute, second, month, day, year)
Exemplul de mai jos creează o dată și o oră cu funcția date() dintr-un număr de parametri în funcția mktime():
<?php
$d=mktime(11, 14, 54, 8, 12, 2014);
echo "Data creerii este " . date("Y-m-d h:i:sa", $d);
?>
Creați o dată dintr-un șir (string) cu strtotime()
Funcția PHP strtotime() este utilizată pentru a converti un șir de date (date string) care poate fi citit de om într-un marcaj de timp (timestamp) Unix (numărul de secunde de la 1 ianuarie 1970, 00:00:00 GMT).
Sintaxă
strtotime(time, now)
Exemplul de mai jos creează o dată și o oră din funcția strtotime():
<?php
$d=strtotime("10:30pm April 15 2014");
echo "Data creerii este " . date("Y-m-d h:i:sa", $d);
?>
PHP este destul de inteligent în ceea ce privește conversia unui șir (string) într-o dată, astfel încât să puteți pune diverse valori:
<?php
$d=strtotime("mâine");
echo date("Y-m-d h:i:sa", $d) . "<br>";
$d=strtotime("sâmbăta viitoare");
echo date("Y-m-d h:i:sa", $d) . "<br>";
$d=strtotime("+ 3 luni"");
echo date("Y-m-d h:i:sa", $d) . "<br>";
?>
Cu toate acestea, strtotime() nu este perfect, așa că nu uitați să verificați șirurile (stringurile) pe care le introduceți acolo.
Mai multe exemple de date
Exemplul de mai jos scoate (outputs) datele pentru următoarele șase sâmbete:
<?php
$startdate = strtotime("Sâmbătă");
$enddate = strtotime("+ 6 săptămâni", $startdate);
while ($startdate < $enddate) {
echo date("M d", $startdate) . "<br>";
$startdate = strtotime("+ 1 săptămână", $startdate);
}
?>
Exemplul de mai jos afișează numărul de zile până la 4 iulie:
<?php
$d1=strtotime("04 iulie");
$d2=ceil(($d1-time())/60/60/24);
echo "Există " . $d2 ." zile până la 4 iulie.";
?>
PHP Include
PHP fișiere include (PHP Include Files)
Instrucțiunea include (sau require) preia tot textul / codul / marcajul (text/code/markup) care există în fișierul specificat și îl copiază în fișierul care folosește instrucțiunea include.
Includerea fișierelor este foarte utilă atunci când doriți să includeți același PHP, HTML sau text în mai multe pagini ale unui site web.
PHP declarațiile include și require (PHP include and require Statements)
Este posibil să inserați conținutul unui fișier PHP într-un alt fișier PHP (înainte ca serverul să îl execute), cu instrucțiunea include sau require.
Instrucțiunile include și require sunt identice, cu excepția eșecului:
require va produce o eroare fatală (E_COMPILE_ERROR) și va opri scriptul
include va produce doar un avertisment (E_WARNING) și scriptul va continua
Așadar, dacă doriți ca execuția să continue și să le arate utilizatorilor ieșirea (output), chiar dacă fișierul include lipsește, folosiți instrucțiunea include.
În caz contrar, în cazul FrameWork, CMS sau o codificare complexă a aplicației PHP, utilizați întotdeauna instrucțiunea require pentru a include un fișier cheie pentru fluxul de execuție. Acest lucru va ajuta la evitarea compromiterii securității și integrității aplicației dvs., doar în caz că lipsește accidental un fișier cheie (key file).
Inclusiv fișierele economisesc multă muncă. Aceasta înseamnă că puteți crea un antet, un subsol sau un fișier de meniu (header, footer sau menu file) pentru toate paginile dvs. web. Apoi, când antetul (header) trebuie actualizat, puteți actualiza doar antetul (header) include fișierul (include file).
Sintaxă
include 'filename'; sau require 'filename';
Exemple PHP include
Presupunem că avem un fișier de subsol standard (standard footer file) numit "footer.php", care arată astfel:
<?php
echo "<p>Copyright © 2020-" . date("Y") . " lectii-virtuale.ro</p>";
?>
Pentru a include fișierul de subsol (footer file) într-o pagină, utilizați instrucțiunea include:
<html>
<body>
<h1>Bine ați venit pe prima mea pagină!</h1>
<p>Un text.</p>
<p>Mai mult text.</p>
<?php include 'footer.php';?>
</body>
</html>
Presupunem că avem un fișier meniu standard (standard menu file) numit "menu.php":
<?php
echo '<a href="/default.asp">Home</a> -
<a href="/html/default.asp">Tutorial HTML</a> -
<a href="/css/default.asp">Tutorial CSS</a> -
<a href="/js/default.asp">Tutorial JavaScript</a> -
<a href="default.asp">Tutorial PHP</a>';
?>
Toate paginile de pe site-ul web ar trebui să folosească acest fișier meniu. Iată cum se poate face (folosim un element <div> pentru ca meniul să poată fi ușor stilat mai târziu cu CSS):
<html>
<body>
<div class="menu">
<?php include 'menu.php';?>
</div>
<h1>Bine ați venit pe prima mea pagină!</h1>
<p>Un text.</p>
<p>Mai mult text.</p>
</body>
</html>
Presupunem că avem un fișier numit "vars.php", cu cateva variabile definite:
<?php
$color='roșu';
$car='BMW';
?>
Apoi, dacă includem fișierul "vars.php", variabilele pot fi utilizate în fișierul apelant:
<html>
<body>
<h1>Bine ați venit pe prima mea pagină!</h1>
<?php include 'vars.php';
echo "Am o $color $car.";
?>
</body>
</html>
PHP include vs. require
Instrucțiunea require este de asemenea folosită pentru a include un fișier în codul PHP.
Cu toate acestea, există o mare diferență între include și require; când un fișier este inclus cu instrucțiunea include și PHP nu îl poate găsi, scriptul va continua să execute:
<html>
<body>
<h1>Bine ați venit pe prima mea pagină!</h1>
<?php include 'noFileExists.php';
echo "Am o $color $car.";
?>
</body>
</html>
Dacă facem același exemplu folosind instrucțiunea require, instrucțiunea echo nu va fi executată, deoarece execuția scriptului moare după ce instrucțiunea require a returnat o eroare fatală:
<html>
<body>
<h1>Bine ați venit pe prima mea pagină!</h1>
<?php require 'noFileExists.php';
echo "Am o $color $car.";
?>
</body>
</html>
Folosiți require când fișierul este solicitat de aplicație.
Folosiți include atunci când fișierul nu este necesar și aplicația ar trebui să continue atunci când fișierul nu este găsit.
PHP Manipularea fișierelor
Manipularea fișierelor PHP (PHP File Handling)
Manipularea fișierelor (File handling) este o parte importantă a oricărei aplicații web. Adesea, trebuie să deschideți și să procesați un fișier pentru diferite sarcini.
PHP Manipularea fișierelor (PHP Manipulating Files)
PHP are mai multe funcții pentru crearea, citirea, încărcarea și editarea fișierelor (creating, reading, uploading, and editing files).
Aveți grijă când manipulați fișierele (manipulating files)!
Când manipulați fișierele (manipulating files) trebuie să fiți foarte atenți.
Puteți face multe daune dacă faceți ceva greșit. Erorile comune sunt: editarea fișierului greșit, completarea unui hard disk cu date nefolositoare (garbage data) și ștergerea din accident a conținutului unui fișier.
Funcția PHP readfile()
Funcția readfile() citește un fișier și îl scrie în bufferul de ieșire (output buffer).
Presupunem că avem un fișier text numit „webdictionary.txt”, stocat pe server, care arată astfel:
AJAX = JavaScript și XML asincron (Asynchronous JavaScript and XML)
CSS = Fișe de stil în cascadă (Cascading Style Sheets)
HTML = Hyper Text Markup Language
PHP = PHP Hypertext Preprocessor
SQL = Limbaj de interogare structurat (Structured Query Language)
SVG = Grafică vectorială scalabilă (Scalable Vector Graphics)
XML = Limbaj de marcare extinsă (EXtensible Markup Language)
Codul PHP pentru a citi fișierul și a-l scrie în bufferul de ieșire (output buffer) este după cum urmează (funcția readfile() returnează numărul de octeți citiți cu succes):
<?php
echo readfile("webdictionary.txt");
?>
Funcția readfile() este utilă dacă tot ce doriți să faceți este să deschideți un fișier și să citiți conținutul acestuia.
Capitolele următoare vă vor învăța mai multe despre gestionarea fișierelor.
PHP Fișierele Open/Read/Close
PHP Fișierele Open/Read/Close
În acest capitol vă vom învăța cum să deschideți, să citiți și să închideți (open, read și close) un fișier pe server.
PHP Open File - fopen()
O metodă mai bună de a deschide fișiere este cu funcția fopen(). Această funcție vă oferă mai multe opțiuni decât funcția readfile().
Vom folosi fișierul text, "webdictionary.txt", în timpul lecțiilor:
AJAX = JavaScript și XML asincron (Asynchronous JavaScript and XML)
CSS = Fișe de stil în cascadă (Cascading Style Sheets)
HTML = Hyper Text Markup Language
PHP = PHP Hypertext Preprocessor
SQL = Limbaj de interogare structurat (Structured Query Language)
SVG = Grafică vectorială scalabilă (Scalable Vector Graphics)
XML = Limbaj de marcare extinsă (EXtensible Markup Language)
Primul parametru al fopen() conține numele fișierului care trebuie deschis și al doilea parametru specifică în ce mod ar trebui să fie deschis fișierul. Următorul exemplu generează, de asemenea, un mesaj dacă funcția fopen() nu poate deschide fișierul specificat:
<?php
$myfile = fopen("webdictionary.txt", "r") or die("Nu se poate deschide fișierul!");
echo fread($myfile,filesize("webdictionary.txt"));
fclose($myfile);
?>
Fișierul poate fi deschis într-unul din următoarele moduri:
r - Deschideți un fișier numai pentru citire. Indicatorul de fișiere începe de la începutul fișierului
w - Deschideți un fișier numai pentru scriere. Șterge conținutul fișierului sau creează un nou fișier dacă acesta nu există. Indicatorul de fișiere începe de la începutul fișierului
a - Deschideți un fișier numai pentru scriere. Datele existente în fișier sunt păstrate. Indicatorul fișierului începe la sfârșitul fișierului. Creează un nou fișier dacă fișierul nu există
x - Creează un nou fișier numai pentru scriere. Returnează FALSE și o eroare dacă fișierul există deja
r + - Deschideți un fișier pentru citire / scriere. Indicatorul de fișiere începe de la începutul fișierului
w + - Deschideți un fișier pentru citire / scriere. Șterge conținutul fișierului sau creează un nou fișier dacă acesta nu există. Indicatorul de fișiere începe de la începutul fișierului
a + - Deschideți un fișier pentru citire / scriere. Datele existente în fișier sunt păstrate. Indicatorul fișierului începe la sfârșitul fișierului. Creează un nou fișier dacă fișierul nu există
x + - Creează un nou fișier pentru citire / scriere. Returnează FALSE și o eroare dacă fișierul există deja
PHP Read File - fread()
Funcția fread() citește dintr-un fișier deschis.
Primul parametru al fread() conține numele fișierului din care trebuie citit și al doilea parametru specifică numărul maxim de octeți de citit.
Următorul cod PHP citește fișierul "webdictionary.txt" până la sfârșit:
fread($myfile,filesize("webdictionary.txt"));
PHP Close File - fclose()
Funcția fclose() este utilizată pentru a închide un fișier deschis.
Este o practică bună de programare pentru a închide toate fișierele după ce ați terminat cu ele. Nu doriți ca un fișier deschis să fie difuzat pe serverul dvs. preluând resurse!
fclose() necesită numele fișierului (sau o variabilă care deține numele fișierului) pe care dorim să o închidem:
<?php
$myfile = fopen("webdictionary.txt", "r");
// ceva cod care urmează să fie executat ....
fclose($myfile);
?>
PHP Read Single Line - fgets()
Funcția fgets() este utilizată pentru a citi o singură linie dintr-un fișier.
Exemplul de mai jos produce (outputs) prima linie a fișierului "webdictionary.txt":
<?php
$myfile = fopen("webdictionary.txt", "r") or die("Nu se poate deschide fișierul!");
echo fgets($myfile);
fclose($myfile);
?>
După un apel la funcția fgets(), indicatorul de fișiere (file pointer) a trecut la linia următoare.
PHP Verifică sfârșitul fișierului - feof() (PHP Check End-Of-File - feof())
Funcția feof() verifică dacă s-a ajuns la „sfârșitul fișierului” (end-of-file) (EOF).
Funcția feof() este utilă pentru a bucla (looping) prin date de lungime necunoscută.
Exemplul de mai jos citește fișierul "webdictionary.txt" linie rând, până la sfârșitul fișierului (end-of-file):
<?php
$myfile = fopen("webdictionary.txt", "r") or die("Nu se poate deschide fișierul!");
// Ieșirea unei linii până la sfârșitul fișierului (end-of-file)
while(!feof($myfile)) {
echo fgets($myfile) . "<br>";
}
fclose($myfile);
?>
PHP Read Single Character - fgetc()
Funcția fgetc() este utilizată pentru a citi un singur caracter dintr-un fișier.
Exemplul de mai jos citește fișierul "webdictionary.txt" caracter după caracter, până când se ajunge la sfârșitul fișierului (end-of-file):
<?php
$myfile = fopen("webdictionary.txt", "r") or die("Nu se poate deschide fișierul!");
// Ieșirea unui caracter până la sfârșitul fișierului (end-of-file)
while(!feof($myfile)) {
echo fgetc($myfile);
}
fclose($myfile);
?>
După un apel către funcția fgetc(), indicatorul de fișier (file pointer) se mută la următorul caracter.
PHP Fișierele Create/Write
PHP Fișierele Create/Write
În acest capitol vă vom învăța cum să creați și să scrieți într-un fișier pe server.
PHP Create File - fopen()
Funcția fopen() este de asemenea folosită pentru a crea un fișier. Poate un pic confuz, dar în PHP, un fișier este creat folosind aceeași funcție folosită pentru a deschide fișiere.
Dacă utilizați fopen() pe un fișier care nu există, acesta îl va crea, având în vedere că fișierul este deschis pentru scriere (writing) (w) sau anexare (appending) (a).
Exemplul de mai jos creează un nou fișier numit "testfile.txt". Fișierul va fi creat în același director în care se află codul PHP:
$myfile = fopen("testfile.txt", "w")
PHP File Permissions
Funcția fwrite() este utilizată pentru a scrie (write) într-un fișier.
Primul parametru fwrite() conține numele fișierului la care trebuie să scrieți (write), iar al doilea parametru este șirul (string) care trebuie scris.
Exemplul de mai jos scrie (write) câteva nume într-un fișier nou numit "newfile.txt":
<?php
$myfile = fopen("newfile.txt", "w") or die("Nu se poate deschide fișierul!");
$txt = "Ion Popescu\n";
fwrite($myfile, $txt);
$txt = "Ioana Popescu\n";
fwrite($myfile, $txt);
fclose($myfile);
?>
Observați că am scris (write) fișierului "newfile.txt" de două ori. De fiecare dată când am scris în fișier, am trimis șirul (stringul) $txt care a conținut mai întâi „Ion Popescu” și al doilea conținut „Ioana Popescu”. După ce am terminat de scris (write), am închis fișierul folosind funcția fclose().
Dacă deschidem fișierul "newfile.txt", ar arăta astfel:
Ion Popescu
Ioana Popescu
Suprascriere PHP (PHP Overwriting)
Acum, că „newfile.txt” conține câteva date, putem arăta ce se întâmplă atunci când deschidem un fișier existent pentru scriere. Toate datele existente vor fi ERASED și vom începe cu un fișier gol.
În exemplul de mai jos, deschidem fișierul nostru existent "newfile.txt" și scriem câteva date noi în el:
<?php
$myfile = fopen("newfile.txt", "w") or die("Nu se poate deschide fișierul!");
$txt = "Mickey Mouse\n";
fwrite($myfile, $txt);
$txt = "Minnie Mouse\n";
fwrite($myfile, $txt);
fclose($myfile);
?>
Dacă acum deschidem fișierul "newfile.txt", atât Ion cât și Ioana au dispărut, și doar datele pe care tocmai le-am scris sunt prezente:
Mickey Mouse
Minnie Mouse
PHP Fișierul Upload
PHP Încărcare fișier (PHP File Upload)
Cu PHP, este ușor să încărcați fișiere pe server.
Cu toate acestea, cu ușurință apare un pericol, așa că întotdeauna aveți grijă atunci când permiteți încărcarea fișierelor!
Configurați fișierul "php.ini"
În primul rând, asigurați-vă că PHP este configurat pentru a permite încărcarea fișierelor.
În fișierul dvs. "php.ini", căutați directiva file_uploads și setați-l pe On:
file_uploads = On
Creați formularul HTML
Apoi, creați un formular HTML care permite utilizatorilor să aleagă fișierul imagine (image file ) pe care doresc să îl încarce:
<!DOCTYPE html>
<html>
<body>
<form action="upload.php" method="post" enctype="multipart/form-data">
Selectați imaginea de încărcat:
<input type="file" name="fileToUpload" id="fileToUpload">
<input type="submit" value="Încărcați imaginea" name="submit">
</form>
</body>
</html>
Câteva reguli de urmat pentru formularul HTML de mai sus:
Asigurați-vă că formularul folosește method="post"
De asemenea, formularul are nevoie de următorul atribut: enctype = "multipart/form-data". Acesta specifică ce tip de conținut (content-type) trebuie utilizat la trimiterea formularului
Fără cerințele de mai sus, încărcarea fișierului nu va funcționa.
Alte lucruri de remarcat:
Atributul type="file" al etichetei (tag) <input> arată câmpul de intrare (input field) ca un control de selectare a fișierelor (file-select control), cu un buton "Browse" lângă controlul de intrare
Formularul de mai sus trimite date unui fișier numit „upload.php”, pe care îl vom crea în continuare.
PHP Creați scriptul de încărcare (Create The Upload File PHP Script)
Fișierul "upload.php" conține codul pentru încărcarea unui fișier:
<?php
$target_dir = "uploads/";
$target_file = $target_dir . basename($_FILES["fileToUpload"]["name"]);
$uploadOk = 1;
$imageFileType = strtolower(pathinfo($target_file,PATHINFO_EXTENSION));
// Verificați dacă fișierul imagine este o imagine reală sau o imagine falsă
if(isset($_POST["submit"])) {
$check = getimagesize($_FILES["fileToUpload"]["tmp_name"]);
if($check !== false) {
echo "Fișierul este o imagine - " . $check["mime"] . ".";
$uploadOk = 1;
} else {
echo "Fișierul nu este o imagine.";
$uploadOk = 0;
}
}
?>
Script PHP explicat:
$target_dir = "uploads/" - specifică directorul în care urmează să fie plasat fișierul
$target_file - specifică calea fișierului care va fi încărcat
$uploadOk=1 - nu este încă utilizat (va fi folosit ulterior)
$imageFileType - reține extensia fișierului (în minuscule/lower case)
În continuare, verificați dacă fișierul imagine este o imagine reală sau o imagine falsă
Va trebui să creați un nou director numit „uploads” în directorul în care se află fișierul „upload.php”. Fișierele încărcate vor fi salvate acolo.
Verificați dacă fișierul există deja
Acum putem adăuga câteva restricții.
În primul rând, vom verifica dacă fișierul există deja în folderul „uploads”. În acest caz, este afișat un mesaj de eroare și $uploadOk este setat la 0:
// Verificați dacă fișierul există deja
if (file_exists($target_file)) {
echo "Ne pare rău, fișierul există deja.";
$uploadOk = 0;
}
Limitați dimensiunea fișierului (Limit File Size)
Câmpul de introducere (input field) a fișierului în formularul nostru HTML de mai sus este denumit "fileToUpload".
Acum, vrem să verificăm dimensiunea fișierului. Dacă fișierul este mai mare de 500KB, este afișat un mesaj de eroare și
$uploadOk este setat la 0:
// Verificați dimensiunea fișierului
if ($_FILES["fileToUpload"]["size"] > 500000) {
echo "Ne pare rău, fișierul dvs. este prea mare.";
$uploadOk = 0;
}
// Permiteți anumite formate de fișiere
if($imageFileType != "jpg" && $imageFileType != "png" && $imageFileType != "jpeg"
&& $imageFileType != "gif" ) {
echo "Ne pare rău, sunt permise doar fișierele JPG, JPEG, PNG și GIF.";
$uploadOk = 0;
}
Încărcați complet scriptul PHP (Complete Upload File PHP Script)
Fișierul complet "upload.php" arată acum astfel:
<?php
$target_dir = "uploads/";
$target_file = $target_dir . basename($_FILES["fileToUpload"]["name"]);
$uploadOk = 1;
$imageFileType = strtolower(pathinfo($target_file,PATHINFO_EXTENSION));
// Verificați dacă fișierul imagine este o imagine reală sau o imagine falsă
if(isset($_POST["submit"])) {
$check = getimagesize($_FILES["fileToUpload"]["tmp_name"]);
if($check !== false) {
echo "Fișierul este o imagine - " . $check["mime"] . ".";
$uploadOk = 1;
} else {
echo "Fișierul nu este o imagine.";
$uploadOk = 0;
}
}
// Verificați dacă fișierul există deja
if (file_exists($target_file)) {
echo "Ne pare rău, fișierul există deja.";
$uploadOk = 0;
}
// Verificați dimensiunea fișierului
if ($_FILES["fileToUpload"]["size"] > 500000) {
echo "Ne pare rău, fișierul dvs. este prea mare.";
$uploadOk = 0;
}
// Permiteți anumite formate de fișiere
if($imageFileType != "jpg" && $imageFileType != "png" && $imageFileType != "jpeg"
&& $imageFileType != "gif" ) {
echo "Ne pare rău, sunt permise doar fișierele JPG, JPEG, PNG și GIF.";
$uploadOk = 0;
}
// Verificați dacă $uploadOk este setat la 0 printr-o eroare
if ($uploadOk == 0) {
echo "Ne pare rău, fișierul dvs. nu a fost încărcat.";
// dacă totul este în regulă, încercați să încărcați fișierul
} else {
if (move_uploaded_file($_FILES["fileToUpload"]["tmp_name"], $target_file)) {
echo "Fișierul ". basename( $_FILES["fileToUpload"]["name"]). " a fost încărcat.";
} else {
echo "Ne pare rău, a fost o eroare la încărcarea fișierului.";
}
}
?>
PHP Cookies
Cookie-uri PHP (PHP Cookies)
Ce este un Cookie?
Un cookie este adesea folosit pentru a identifica un utilizator. Un cookie este un fișier mic pe care serverul îl încorporează pe computerul utilizatorului. De fiecare dată când același computer solicită o pagină cu un browser, va trimite și cookie-ul. Cu PHP, puteți crea și recupera valorile cookie.
Creați cookie-uri cu PHP
Un cookie este creat cu funcția setcookie().
Sintaxă
setcookie(name, value, expire, path, domain, secure, httponly);
Numai parametrul name este necesar. Toți ceilalți parametrii sunt opționali.
PHP Creare / Recuperare Cookie (PHP Create/Retrieve a Cookie)
Următorul exemplu creează un cookie numit „user” cu valoarea „Ion Popescu”. Cookie-ul va expira după 30 de zile (86400 * 30).
„/” înseamnă că cookie-ul este disponibil pe întregul site web (în caz contrar, selectați directorul preferat).
Vom prelua apoi valoarea „user” cookie-ului (folosind variabila globală $_COOKIE). De asemenea, folosim funcția isset() pentru a afla dacă cookie-ul este setat:
<?php
$cookie_name = "user";
$cookie_value = "Ion Popescu";
setcookie($cookie_name, $cookie_value, time() + (86400 * 30), "/"); // 86400 = 1 day
?>
<html>
<body>
<?php
if(!isset($_COOKIE[$cookie_name])) {
echo "Cookie-ul numit" . $cookie_name . "' nu este setat!";
} else {
echo "Cookie '" . $cookie_name . "' is set!<br>";
echo "Valoarea este:" . $_COOKIE[$cookie_name];
}
?>
</body>
</html>
Funcția setcookie() trebuie să apară BEFORE de eticheta (tag) <html>.
Valoarea cookie-ului este codificată în mod automat la trimiterea cookie-ului și automat decodificată atunci când este primită (pentru a preveni codificarea URL-ului, utilizați în schimb setrawcookie()).
Modificați o valoare cookie
Pentru a modifica un cookie, trebuie doar să setați (din nou) modul cookie folosind funcția setcookie():
<?php
$cookie_name = "user";
$cookie_value = "Alex Ionescu";
setcookie($cookie_name, $cookie_value, time() + (86400 * 30), "/");
?>
<html>
<body>
<?php
if(!isset($_COOKIE[$cookie_name])) {
echo "Cookie-ul nimit'" . $cookie_name . "' nu este setat!";
} else {
echo "Cookie'" . $cookie_name . "' este setat!<br>";
echo "Valoarea este:" . $_COOKIE[$cookie_name];
}
?>
</body>
</html>
Ștergeți un cookie
Pentru a șterge un cookie, utilizați funcția setcookie() cu o dată de expirare din trecut:
<?php
// setați data de expirare la o oră în urmă
setcookie("user", "", time() - 3600);
?>
<html>
<body>
<?php
echo "Cookie 'user' este șters.";
?>
</body>
</html>
Verificați dacă cookie-urile sunt activate
Următorul exemplu creează un mic script care verifică dacă cookie-urile sunt activate. Mai întâi, încercați să creați un cookie de testare cu funcția setcookie(), apoi numărați variabila array $_COOKIE:
<?php
setcookie("test_cookie", "test", time() + 3600, '/');
?>
<html>
<body>
<?php
if(count($_COOKIE) > 0) {
echo "Cookie-urile sunt activate.";
} else {
echo "Cookie-urile sunt dezactivate.";
}
?>
</body>
</html>
PHP Sesiuni
Sesiuni PHP
O sesiune este o modalitate de a stoca informații (în variabile) pentru a fi utilizate în mai multe pagini.
Spre deosebire de un cookie, informațiile nu sunt stocate pe computerul utilizatorilor.
Ce este o sesiune PHP?
Când lucrați cu o aplicație, o deschideți, faceți unele modificări și apoi o închideți. Aceasta seamănă foarte mult cu o sesiune. Calculatorul știe cine ești. Știe când porniți aplicația și când terminați. Dar pe internet există o problemă: serverul web nu știe cine sunteți sau ce faceți, deoarece adresa HTTP nu menține starea.
Variabilele de sesiune (session variables) rezolvă această problemă prin stocarea informațiilor utilizatorului care vor fi utilizate pe mai multe pagini (de exemplu, numele de utilizator, culoarea preferată etc.). În mod implicit, variabilele de sesiune durează până când utilizatorul închide browserul.
Așa deci; Variabilele de sesiune (session variables) conțin informații despre un singur utilizator și sunt disponibile pentru toate paginile dintr-o singură aplicație.
Dacă aveți nevoie de o stocare permanentă, poate doriți să stocați datele într-o bază de date.
Porniți o sesiune PHP
O sesiune este pornită cu funcția session_start().
Variabilele de sesiune sunt setate cu variabila globală PHP: $_SESSION.
Acum, hai să creăm o nouă pagină numită "demo_session1.php". În această pagină, începem o nouă sesiune PHP și setăm câteva variabile de sesiune:
<?php
// Începeți sesiunea
session_start();
?>
<!DOCTYPE html>
<html>
<body>
<?php
// Setați variabile de sesiune
$_SESSION["favcolor"] = "green";
$_SESSION["favanimal"] = "cat";
echo "Variabilele de sesiune sunt setate.";
?>
</body>
</html>
Funcția session_start() trebuie să fie primul lucru din documentul dvs. Înainte de orice etichete HTML.
Obțineți valori variabile ale sesiunii PHP
În continuare, creem o altă pagină numită "demo_session2.php". Din această pagină, vom accesa informațiile de sesiune pe care le-am setat pe prima pagină („demo_session1.php”).
Observați că variabilele de sesiune nu sunt transmise individual la fiecare pagină nouă, ci sunt preluate din sesiunea pe care o deschidem la începutul fiecărei pagini (session_start()).
De asemenea, observați că toate valorile variabilei de sesiune sunt stocate în variabila globală $_SESSION:
<?php
session_start();
?>
<!DOCTYPE html>
<html>
<body>
<?php
// Variabilele de sesiune echo care au fost setate pe pagina anterioară
echo "Culoarea preferată este " . $_SESSION["favcolor"] . ".<br>";
echo "Animalul preferat este " . $_SESSION["favanimal"] . ".";
?>
</body>
</html>
Un alt mod de a arăta toate valorile variabilei de sesiune (session variable) pentru o sesiune de utilizator (user session ) este să executați următorul cod:
<?php
session_start();
?>
<!DOCTYPE html>
<html>
<body>
<?php
print_r($_SESSION);
?>
</body>
</html>
Cum functioneazã? De unde știe că sunt eu?
Majoritatea ședințelor setează o cheie de utilizator (user-key) pe computerul utilizatorului care arată așa: 765487cf34ert8dede5a562e4f3a7e12. Apoi, când o sesiune este deschisă pe o altă pagină, scanează computerul pentru o cheie de utilizator (user-key). Dacă există o potrivire, aceasta accesează sesiunea, dacă nu, începe o nouă sesiune.
Modificați o variabilă de sesiune PHP
Pentru a schimba o variabilă de sesiune, trebuie doar să o suprascrieți:
<?php
session_start();
?>
<!DOCTYPE html>
<html>
<body>
<?php
// pentru a schimba o variabilă de sesiune, trebuie doar să o rescrieți
$_SESSION["favcolor"] = "yellow";
print_r($_SESSION);
?>
</body>
</html>
Distrugeți o sesiune PHP
Pentru a elimina toate variabilele globale ale sesiunii și a distruge sesiunea, utilizați session_unset() și session_destroy():
<?php
session_start();
?>
<!DOCTYPE html>
<html>
<body>
<?php
// eliminați toate variabilele de sesiune
session_unset();
// distrugeți sesiunea
session_destroy();
?>
</body>
</html>
PHP Filtre
Filtre PHP
Validarea datelor = Determinați dacă datele sunt într-o formă corectă.
Sanitizarea datelor = Eliminați orice caracter ilegal din date.
Extensia de filtrare PHP
Filtrele PHP sunt utilizate pentru validarea și igienizarea intrărilor externe.
Extensia de filtru PHP are multe dintre funcțiile necesare pentru verificarea intrării utilizatorului (user input) și este concepută pentru a face validarea datelor mai ușoară și mai rapidă.
Funcția filter_list() poate fi utilizată pentru a enumera ce oferă extensia de filtru PHP:
<table>
<tr>
<td>Nume filtru</td>
<td>ID filtru</td>
</tr>
<?php
foreach (filter_list() as $id =>$filter) {
echo '<tr><td>' . $filter . '</td><td>' . filter_id($filter) . '</td></tr>';
}
?>
</table>
De ce să folosești filtrele?
Multe aplicații web primesc input extern. Intrarea/datele externe pot fi:
Intrarea utilizatorului dintr-un formular (User input from a form)
Cookies
Date despre servicii web (Web services data)
Variabilele serverului (Server variables)
Rezultatele interogării bazei de date (Database query results)
Ar trebui să validați întotdeauna datele externe!
Datele trimise nevalide pot duce la probleme de securitate și vă pot break pagina web!
Folosind filtre PHP puteți fi sigur că aplicația dvs. primește introducerea corectă!
Funcția PHP filter_var()
Funcția filter_var() validează și igienizează datele.
Funcția filter_var() filtrează o singură variabilă cu un filtru specificat. Este nevoie de două bucăți de date (pieces of data):
Variabila pe care doriți să o verificați
Tipul de verificare de utilizat
Sanitizarea unui string
Următorul exemplu utilizează funcția filter_var() pentru a elimina toate etichetele HTML dintr-un șir (string):
<?php
$str = "<h1>Hello World!</h1>";
$newstr = filter_var($str, FILTER_SANITIZE_STRING);
echo $newstr;
?>
Validarea unui număr întreg (integer)
Următorul exemplu utilizează funcția filter_var() pentru a verifica dacă variabila $int este un număr întreg (integer). Dacă $int este un număr întreg (integer), rezultatul codului de mai jos va fi: „Integer este valid”. Dacă $int nu este un număr întreg (integer), rezultatul va fi: „Integer nu este valid”:
<?php
$int = 100;
if (!filter_var($int, FILTER_VALIDATE_INT) === false) {
echo("Integer este valid");
} else {
echo("Integer nu este valid");
}
?>
filter_var() și Problema cu 0
În exemplul de mai sus, dacă $int a fost setat pe 0, funcția de mai sus va returna „Integer nu este valid”. Pentru a rezolva această problemă, utilizați codul de mai jos:
<?php
$int = 0;
if (filter_var($int, FILTER_VALIDATE_INT) === 0 || !filter_var($int, FILTER_VALIDATE_INT) === false) {
echo("Integer este valid");
} else {
echo("Integer nu este valid");
}
?>
Validați o adresă IP
Următorul exemplu utilizează funcția filter_var() pentru a verifica dacă variabila $ip este o adresă IP validă:
<?php
$ip = "127.0.0.1";
if (!filter_var($ip, FILTER_VALIDATE_IP) === false) {
echo("$ip este o adresă IP validă");
} else {
echo("$ip nu este o adresă IP validă");
}
?>
Sanitizarea și validarea unei adrese e-mail
Următorul exemplu utilizează funcția filter_var() pentru a elimina mai întâi toate caracterele ilegale din variabila $e-mail, apoi verificați dacă este o adresă e-mail validă:
<?php
$email = "[email protected]";
// Eliminați toate caracterele ilegale din e-mail
$email = filter_var($email, FILTER_SANITIZE_EMAIL);
// Validați e-mail
if (!filter_var($email, FILTER_VALIDATE_EMAIL) === false) {
echo("$email este o adresă e-mail validă");
} else {
echo("$email nu este o adresă e-mail validă");
}
?>
Sanitizarea și validarea unei adrese URL
Următorul exemplu utilizează funcția filter_var() pentru a elimina mai întâi toate caracterele ilegale dintr-o adresă URL, apoi verificați dacă $url este o adresă URL validă:
<?php
$url = "https://www.w3schools.com";
// Eliminați toate caracterele ilegale dintr-un URL
$url = filter_var($url, FILTER_SANITIZE_URL);
// Validați adresa URL
if (!filter_var($url, FILTER_VALIDATE_URL) === false) {
echo("$url este o adresă URL validă");
} else {
echo("$url nu este o adresă URL validă");
}
?>
PHP Filtre avansate
Filtre PHP avansate
Validați un număr întreg (integer) într-un interval
Următorul exemplu utilizează funcția filter_var() pentru a verifica dacă o variabilă este atât de tip INT, cât și între 1 și 200:
<?php
$int = 122;
$min = 1;
$max = 200;
if (filter_var($int, FILTER_VALIDATE_INT, array("options" => array("min_range"=>$min, "max_range"=>$max))) === false) {
echo("Valoarea variabilă nu se încadrează în intervalul legal");
} else {
echo("Valoarea variabilă se încadrează în intervalul legal");
}
?>
Validați adresa IPv6
Următorul exemplu utilizează funcția filter_var() pentru a verifica dacă variabila $ip este o adresă IPv6 validă:
<?php
$ip = "2001:0db8:85a3:08d3:1319:8a2e:0370:7334";
if (!filter_var($ip, FILTER_VALIDATE_IP, FILTER_FLAG_IPV6) === false) {
echo("$ip este o adresă IPv6 validă");
} else {
echo("$ip nu este o adresă IPv6 validă");
}
?>
Validați adresa URL - trebuie să conțină QueryString
Următorul exemplu utilizează funcția filter_var() pentru a verifica dacă variabila $url este o adresă URL cu un șir de interogare (querystring):
<?php
$url = "https://www.lectii-virtuale.ro";
if (!filter_var($url, FILTER_VALIDATE_URL, FILTER_FLAG_QUERY_REQUIRED) === false) {
echo("$url este o adresă URL validă cu un șir de interogare (query string)");
} else {
echo("$url nu este o adresă URL validă cu un șir de interogare (query string)");
}
?>
Eliminați caracterele cu valoarea ASCII>127
Următorul exemplu utilizează funcția filter_var() pentru igienizarea unui șir (string). Ambele vor elimina din șir (string) toate etichetele HTML și toate caracterele cu valoarea ASCII>127:
<?php
$str = "<h1>Hello WorldÆØÅ!</h1>";
$newstr = filter_var($str, FILTER_SANITIZE_STRING, FILTER_FLAG_STRIP_HIGH);
echo $newstr;
?>
PHP JSON
PHP și JSON
Ce este JSON?
JSON reprezintă o notare a obiectului JavaScript (JavaScript Object Notation) și este o sintaxă pentru stocarea și schimbul de date.
Deoarece formatul JSON este un format bazat pe text (text-based format), acesta poate fi trimis cu ușurință la și de la un server și utilizat ca format de date de orice limbaj de programare.
PHP și JSON
PHP are unele funcții integrate (built-in functions) pentru a gestiona JSON.
În primul rând, vom analiza următoarele două funcții:
json_encode()
json_decode()
PHP - json_encode()
Funcția json_encode() este utilizată pentru a codifica o valoare în formatul JSON.
Acest exemplu arată modul de codificare a unui tablou asociativ (associative array) într-un obiect JSON:
<?php
$age = array("Petre"=>35, "Ion"=>37, "Alex"=>43);
echo json_encode($age);
?>
Acest exemplu arată modul de codificare a unui tablou indexat (indexed array) într-un tablou (array) JSON:
<?php
$cars = array("Volvo", "BMW", "Toyota");
echo json_encode($cars);
?>
PHP - json_decode()
Funcția json_decode() este utilizată pentru a decoda un obiect JSON (JSON object) într-un obiect PHP (PHP object) sau într-un tablou asociativ (associative array).
Acest exemplu decodează datele JSON (JSON data) într-un obiect PHP (PHP object):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
var_dump(json_decode($jsonobj));
?>
Funcția json_decode() returnează în mod implicit un obiect. Funcția json_decode() are un al doilea parametru, iar atunci când este setată la adevărat (true), obiectele JSON (JSON objects) sunt decodate în tablele asociative (associative array).
Acest exemplu decodifică datele JSON (JSON data) într-un tablou asociativ PHP (PHP associative array):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
var_dump(json_decode($jsonobj, true));
?>
PHP - Accesarea valorilor decodate
Iată două exemple despre cum să accesați valorile decodate dintr-un obiect și dintr-un tablou asociativ (associative array):
Acest exemplu arată cum să accesați valorile dintr-un obiect PHP (PHP object):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
$obj = json_decode($jsonobj);
echo $obj->Petre;
echo $obj->Ion;
echo $obj->Alex;
?>
Acest exemplu arată cum să accesați valorile dintr-un tablou asociativ PHP (PHP associative array):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
$arr = json_decode($jsonobj, true);
echo $arr["Petre"];
echo $arr["Ion"];
echo $arr["Alex"];
?>
PHP - Buclă prin valori (Looping Through the Values)
De asemenea, puteți bucla (loop) valorile cu o buclă (loop) foreach():
Acest exemplu arată cum să vă buclați (loop) prin valorile unui obiect PHP (PHP object):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
$obj = json_decode($jsonobj);
foreach($obj as $key => $value) {
echo $key . " => " . $value . "<br>";
}
?>
Acest exemplu arată cum să vă buclați (loop) prin valorile unui tablou asociativ PHP (PHP associative array):
<?php
$jsonobj = '{"Petre":35,"Ion":37,"Alex":43}';
$arr = json_decode($jsonobj, true);
foreach($arr as $key => $value) {
echo $key . " => " . $value . "<br>";
}
?>
PHP - OOP
PHP - OOP
PHP - Ce este OOP?
De la PHP5, puteți scrie și cod PHP într-un stil orientat pe obiecte (object-oriented style).
Programarea orientată pe obiecte (Object-Oriented programming) este mai rapidă și mai ușor de executat.
PHP Ce este OOP?
OOP înseamnă programare orientată pe obiecte (Object-Oriented Programming).
Programarea procedurală (Procedural programming) se referă la scrierea procedurilor sau a funcțiilor care efectuează operațiuni asupra datelor, în timp ce programarea orientată pe obiect (object-oriented programming) este despre crearea de obiecte care conțin atât date cât și funcții.
Programarea orientată pe obiecte (object-oriented programming) are mai multe avantaje față de programarea procedurală (procedural programming):
OOP este mai rapid și mai ușor de executat
OOP oferă o structură clară pentru programe
OOP ajută la păstrarea codului PHP DRY „Nu vă repetați” (Don't Repeat Yourself) și face codul mai ușor de întreținut, modificat și depanat
OOP face posibilă crearea de aplicații reutilizabile complete, cu mai puțin cod și timp de dezvoltare mai scurt
Principiul „Nu vă repetați” (Don't Repeat Yourself) (DRY) se referă la reducerea repetării codului. Ar trebui să extrageți codurile care sunt comune pentru aplicație și să le așezați într-un singur loc și să le reutilizați în loc să le repetați.
PHP - Ce sunt clasele și obiectele?
Clasele și obiectele sunt cele două aspecte principale ale programării orientate pe obiecte (object-oriented programming).
Diferența dintre clasă și obiecte.
O clasă este un șablon pentru obiecte (template for objects), iar un obiect este o instanță a unei clase.
Când obiectele individuale sunt create, moștenesc toate proprietățiile și comportamentele din clasă, dar fiecare obiect va avea valori diferite pentru proprietăți.
Uitați-vă la capitolele următoare pentru a afla mai multe despre OOP.
PHP OOP - clase și obiecte
PHP OOP - clase și obiecte
O clasă este un șablon pentru obiecte (template for objects), iar un obiect este o instanță a clasei.
Cazul OOP
Să presupunem că avem o clasă numită Fruit. Un fruct poate avea proprietăți precum numele, culoarea, greutatea, etc (name, color, weight). Putem defini variabile precum $nume, $culoare și $greutate ($name, $color, and $weight) pentru a reține valorile acestor proprietăți.
Când sunt create obiectele individuale (măr, banană/apple, banana, etc.), moștenesc toate proprietățiile și comportamentele din clasă, dar fiecare obiect va avea valori diferite pentru proprietăți.
Definiți o clasă
O clasă este definită folosind cuvântul cheie al clasei (class keyword), urmată de numele clasei și de o pereche de acolade ({}). Toate proprietățiile și metodele sale se încadrează în acolade:
Sintaxă
<?php
class Fruit {
// codul merge aici ...
?>
Mai jos declarăm o clasă numită Fruit compusă din două proprietăți ($nume și $culoare/$name and $color) și două metode set_name() și get_name() pentru setarea și obținerea proprietății $nume ($name):
<?php
class Fruit {
// Proprietăți
public $name;
public $color;
// Metode
function set_name($name) {
$this->name = $name;
}
function get_name() {
return $this->name;
}
}
?>
Într-o clasă, variabilele se numesc proprietăți și funcțiile se numesc metode!
Definiți obiectele
Clasele nu sunt nimic fără obiecte! Putem crea mai multe obiecte dintr-o clasă. Fiecare obiect are toate proprietățiile și metodele definite în clasă, dar vor avea valori de proprietate (property values) diferite.
Obiectele unei clase sunt create folosind noul cuvânt cheie ( new keyword).
În exemplul de mai jos, $apple și $banana sunt exemple ale clasei Fruit:
<?php
class Fruit {
// Proprietăți
public $name;
public $color;
// Metode
function set_name($name) {
$this->name = $name;
}
function get_name() {
return $this->name;
}
}
$apple = new Fruit();
$banana = new Fruit();
$apple->set_name('Apple');
$banana->set_name('Banana');
echo $apple->get_name();
echo "<br>";
echo $banana->get_name();
?>
În exemplul de mai jos, adăugăm încă două metode la clasa Fruit, pentru setarea și obținerea proprietății $color:
<?php
class Fruit {
// Proprietăți
public $name;
public $color;
// Metode
function set_name($name) {
$this->name = $name;
}
function get_name() {
return $this->name;
}
function set_color($color) {
$this->color = $color;
}
function get_color() {
return $this->color;
}
}
$apple = new Fruit();
$apple->set_name('Apple');
$apple->set_color('Red');
echo "Name: " . $apple->get_name();
echo "<br>";
echo "Color: " . $apple->get_color();
?>
PHP - Cuvântul cheie (Keyword) $this
Cuvântul cheie (Keyword) $this se referă la obiectul curent (current object) și este disponibil numai în cadrul metodelor.
Priviți următorul exemplu:
<?php
class Fruit {
public $name;
}
$apple = new Fruit();
?>
Deci, unde putem schimba valoarea proprietății $name? Există două moduri:
În interiorul clasei (adăugând o metodă set_name() și utilizați $this):
<?php
class Fruit {
public $name;
function set_name($name) {
$this->name = $name;
}
}
$apple = new Fruit();
$apple->set_name("Apple");
?>
În afara clasei (modificând direct valoarea proprietății):
<?php
class Fruit {
public $name;
}
$apple = new Fruit();
$apple->name = "Apple";
?>
PHP - instanceof
Puteți utiliza cuvântul cheie instanceof (instanceof keyword) pentru a verifica dacă un obiect aparține unei clase specifice:
<?php
$apple = new Fruit();
var_dump($apple instanceof Fruit);
?>
PHP OOP - Constructor
PHP OOP - Constructor
PHP - Funcția __construct
Un constructor vă permite să inițializați proprietățiile unui obiect la crearea obiectului.
Dacă creați o funcție __construct(), PHP va apela automat această funcție atunci când creați un obiect dintr-o clasă.
Observați că funcția construct începe cu două underscores (__)!
În exemplul de mai jos vedem că folosirea unui constructor ne scutește de la apelarea metodei set_name() care reduce cantitatea de cod:
<?php
class Fruit {
public $name;
public $color;
function __construct($name) {
$this->name = $name;
}
function get_name() {
return $this->name;
}
}
$apple = new Fruit("Apple");
echo $apple->get_name();
?>
Alt exemplu:
<?php
class Fruit {
public $name;
public $color;
function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
function get_name() {
return $this->name;
}
function get_color() {
return $this->color;
}
}
$apple = new Fruit("Apple", "red");
echo $apple->get_name();
echo "<br>";
echo $apple->get_color();
?>
PHP OOP - Destructor
PHP OOP - Destructor
PHP - Funcția __destruct
Se numește un destructor atunci când obiectul este distrus sau scriptul este oprit sau ieșit.
Dacă creați o funcție __destruct(), PHP va apela automat această funcție la sfârșitul scriptului.
Observați că funcția destruct începe cu două sublinieri (underscores) (__)!
Exemplul de mai jos are o funcție __construct() care se numește automat atunci când creați un obiect dintr-o clasă și o funcție __destruct() care este apelată automat la sfârșitul scriptului:
<?php
class Fruit {
public $name;
public $color;
function __construct($name) {
$this->name = $name;
}
function __destruct() {
echo "The fruit is {$this->name}.";
}
}
$apple = new Fruit("Apple");
?>
Alt exemplu:
<?php
class Fruit {
public $name;
public $color;
function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
function __destruct() {
echo "Fructul este {$this->name} și culoarea este {$this->color}.";
}
}
$apple = new Fruit("Apple", "red");
?>
Deoarece constructorii și distrugătorii (constructors and destructors) ajută la reducerea cantității de cod, sunt foarte utili!
PHP OOP - Modificatori access
PHP OOP - Modificatori access
PHP - Modificatori access
Proprietățile și metodele pot avea modificatori access care controlează unde pot fi accesate.
Există trei modificatori de acces:
public - proprietatea sau metoda poate fi accesată de oriunde.
Aceasta este implicită
protected - proprietatea sau metoda poate fi accesată în cadrul clasei și prin clase derivate din acea clasă
private - proprietatea sau metoda pot fi accesate DOAR în cadrul clasei
În exemplul următor, am adăugat trei modificatori access diferiți la cele trei proprietăți. Aici, dacă încercați să setați numele proprietății (name property), va funcționa bine (deoarece numele proprietății (name property) este public).
Cu toate acestea, dacă încercați să setați culoarea sau greutatea proprietății (color and weight property), aceasta va duce la o eroare fatală (deoarece proprietățiile de culoare și greutate (color and weight property) sunt protejate și private):
<?php
class Fruit {
public $name;
protected $color;
private $weight;
}
$mango = new Fruit();
$mango->name = 'Mango'; // OK
$mango->color = 'Yellow'; // ERROR
$mango->weight = '300'; // ERROR
?>
În următorul exemplu, am adăugat modificatori access la două metode.
Aici, dacă încercați să apelați funcția set_color() sau set_weight(), va rezulta o eroare fatală (fatal error) (deoarece cele două funcții sunt considerate protejate și private), chiar dacă toate proprietățiile sunt publice:
<?php
class Fruit {
public $name;
public $color;
public $weight;
function set_name($n) { // o funcție publică (implicit)
$this->name = $n;
}
protected function set_color($n) { // o funcție protejată
$this->color = $n;
}
private function set_weight($n) { // o funcție privată
$this->weight = $n;
}
}
$mango = new Fruit();
$mango->set_name('Mango'); // OK
$mango->set_color('Yellow'); // ERROR
$mango->set_weight('300'); // ERROR
?>
PHP OOP - Moștenire
PHP OOP - Inheritance
PHP - Ce este Inheritance?
Inheritance în OOP = Când o clasă derivă dintr-o altă clasă.
Clasa child (copil) va moșteni toate proprietățiile și metodele publice și protejate de la clasa parent (părinte). În plus, poate avea propriile sale proprietăți și metode.
O clasă inherited (moștenită) este definită folosind cuvântul cheie extensie (extends keyword).
Să ne uităm la un exemplu:
<?php
class Fruit {
public $name;
public $color;
public function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
public function intro() {
echo "Fructul este {$this->name} și culoarea este {$this->color}.";
}
}
// Strawberry este moștenită (inherited) de la Fruit
class Strawberry extends Fruit {
public function message() {
echo "Am I a fruit or a berry? ";
}
}
$strawberry = new Strawberry("Strawberry", "red");
$strawberry->message();
$strawberry->intro();
?>
Exemplu explicat
Clasa Strawberry este moștenită (inherited) de la clasa Fruit.
Aceasta înseamnă că clasa Strawberry poate folosi numele public $name și proprietățiile $color, precum și metodele publice __construct() și intro() din clasa Fruit din cauza moștenirii (inheritance).
Clasa Strawberry are, de asemenea, propria sa metodă: message().
PHP - Inheritance și modificator access protejat
În capitolul anterior am aflat că proprietățiile sau metodele protejate pot fi accesate în cadrul clasei și prin clase derivate din acea clasă. Ce inseamna asta?
Să ne uităm la un exemplu:
<?php
class Fruit {
public $name;
public $color;
public function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
protected function intro() {
echo "Fructul este {$this->name} și culoarea este {$this->color}.";
}
}
class Strawberry extends Fruit {
public function message() {
echo "Sunt un fruit sau o berry? ";
}
}
// Încercați să apelați toate cele trei metode din afara clasei
$strawberry = new Strawberry("Strawberry", "red"); // OK. __construct() este public
$strawberry->message(); // OK. message() este public
$strawberry->intro(); // ERROR. intro() este protejat
?>
În exemplul de mai sus vedem că dacă încercăm să apelăm la o metodă protejată (intro()) din afara clasei, vom primi o eroare. Metodele publice vor funcționa bine!
Să ne uităm la un alt exemplu:
<?php
class Fruit {
public $name;
public $color;
public function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
protected function intro() {
echo "Fructul este{$this->name} și culoarea este {$this->color}.";
}
}
class Strawberry extends Fruit {
public function message() {
echo "Sunt un fruit sau o berry? ";
// Apelați metoda protejată din cadrul clasei derivate - OK
$this -> intro();
}
}
$strawberry = new Strawberry("Strawberry", "red"); // OK. __construct() este public
$strawberry->message(); // OK. message() este public și apelează intro() (care este protejat) din cadrul clasei derivate
?>
În exemplul de mai sus vedem că toate funcționează bine! Se datorează faptului că numim metoda protejată (intro()) din interiorul clasei derivate.
PHP - Overriding Inherited Methods
Metodele moștenite (Inherited methods) pot fi anulate prin redefinirea metodelor (folosiți același nume) în clasa child (copil).
Priviți exemplul de mai jos. Metodele __construct() și intro() din clasa child (copil) (Strawberry) vor înlocui metodele __construct() și intro() din clasa parent (părinte) (Fruit):
<?php
class Fruit {
public $name;
public $color;
public function __construct($name, $color) {
$this->name = $name;
$this->color = $color;
}
public function intro() {
echo "Fructul este {$this->name} și culoarea este {$this->color}.";
}
}
class Strawberry extends Fruit {
public $weight;
public function __construct($name, $color, $weight) {
$this->name = $name;
$this->color = $color;
$this->weight = $weight;
}
public function intro() {
echo "Fructul este {$this->name}, culoarea este {$this->color}, și greutatea este {$this->weight} gram.";
}
}
$strawberry = new Strawberry("Strawberry", "red", 50);
$strawberry->intro();
?>
PHP - Cuvântul cheie final
Cuvântul cheie final (the final keyword) poate fi utilizat pentru a preveni moștenirea clasei (class inheritance) sau pentru a preveni suprasolicitarea metodei (method overriding).
Următorul exemplu arată cum să preveniți moștenirea clasei (class inheritance):
<?php
final class Fruit {
// ceva cod
}
// va duce la eroare
class Strawberry extends Fruit {
// ceva cod
}
?>
<?php
class Fruit {
final public function intro() {
// ceva cod
}
}
class Strawberry extends Fruit {
// va duce la eroare
public function intro() {
// ceva cod
}
}
?>
PHP OOP - Constante
PHP OOP - Constante de clasă (PHP OOP - Class Constants)
PHP - Constante de clasă (PHP - Class Constants)
Constantele nu pot fi schimbate odată ce sunt declarate.
Constantele de clasă (Class constants) pot fi utile dacă trebuie să definiți unele date constante (constant data) dintr-o clasă.
O constantă de clasă (class constant) este declarată în interiorul unei clase cu ajutorul cuvântului cheie (keyword) const.
Constantele de clasă (class constants) sunt case-sensitive. Cu toate acestea, se recomandă numirea constantelor cu litere mari (uppercase letters).
Putem accesa o constantă din afara clasei folosind numele clasei (class name) urmată de operatorul de rezoluție al domeniului (::) urmată de numele constant (constant name), cum este aici:
<?php
class Goodbye {
const LEAVING_MESSAGE = "Vă mulțumim că ați vizitat lectii-virtuale.ro!";
}
echo Goodbye::LEAVING_MESSAGE;
?>
Sau, putem accesa o constantă din interiorul clasei folosind cuvântul cheie (keyword) auto urmat de operatorul de rezoluție de aplicare (::) urmat de numele constant (constant name), cum este aici:
<?php
class Goodbye {
const LEAVING_MESSAGE = "Vă mulțumim că ați vizitat lectii-virtuale.ro!";
public function byebye() {
echo self::LEAVING_MESSAGE;
}
}
$goodbye = new Goodbye();
$goodbye->byebye();
?>
PHP OOP - Clase abstracte
PHP OOP - Clase abstracte
PHP - Care sunt clasele și metodele abstracte?
Clasele și metodele abstracte sunt atunci când clasa parent (părinte) are o metodă numită, dar au nevoie de o clasă (e) child (copil) pentru a finaliza sarcinile.
O clasă abstractă (abstract class) este o clasă care conține cel puțin o metodă abstractă (abstract method). O metodă abstractă (abstract method) este o metodă care este declarată, dar care nu este implementată în cod.
O clasă sau o metodă abstractă (abstract method) este definită de cuvântul cheie (keyword) abstract:
Sintaxă
<?php
abstract class ParentClass {
abstract public function someMethod1();
abstract public function someMethod2($name, $color);
abstract public function someMethod3() : string;
}
?>
La moștenirea (inheriting) de la o clasă abstractă (abstract class), metoda clasei copil (child class method) trebuie definită cu același nume și cu același modificator access mai puțin restricționat. Deci, dacă metoda abstractă (abstract method) este definită ca protejată, metoda clasei copil (child class method) trebuie definită fie protejată, fie publică, dar nu privată. De asemenea, tipul și numărul de argumente solicitate trebuie să fie aceleași. Cu toate acestea, clasele pentru copii (child classes) pot avea în plus argumente opționale.
Deci, atunci când o clasă de copii (child class) este moștenită (inherited) de la o clasă abstractă (abstract class), avem următoarele reguli:
Metoda clasei copil (child class method) trebuie definită cu același nume și redeclarea metodei abstracte părinte (parent abstract method).
Metoda clasei pentru copii (child class method) trebuie definită cu același sau cu un mai puțin restricționat modificator access.
Numărul de argumente solicitate trebuie să fie același. Cu toate acestea, clasa pentru copii (child class) poate avea în plus argumente opționale.
<?php
// Clasa părinte (Parent class)
abstract class Car {
public $name;
public function __construct($name) {
$this->name = $name;
}
abstract public function intro() : string;
}
// Clasele copil(Child classes)
class Audi extends Car {
public function intro() : string {
return "Alege calitatea germană! Sunt un $this->name!";
}
}
class Volvo extends Car {
public function intro() : string {
return "Mândru că sunt suedez! Sunt un $this->name!";
}
}
class Citroen extends Car {
public function intro() : string {
return "Extravaganța franceză! Sunt un a $this->name!";
}
}
// Creați obiecte din clasele copil (child classes)
$audi = new audi("Audi");
echo $audi->intro();
echo "<br>";
$volvo = new volvo("Volvo");
echo $volvo->intro();
echo "<br>";
$citroen = new citroen("Citroen");
echo $citroen->intro();
?>
Exemplu explicat
Clasele Audi, Volvo și Citroen sunt moștenite (inherited) de la clasa Auto. Aceasta înseamnă că clasele Audi, Volvo și Citroen pot utiliza proprietatea publică $name precum și metoda publică __construct() din clasa Car din cauza moștenirii (inheritance).
Dar, intro() este o metodă abstractă (abstract method) care ar trebui definită în toate clasele copil (child classes) și ar trebui să returneze un șir (string).
PHP - mai multe exemple de clase abstracte
Să ne uităm la un alt exemplu în care metoda abstractă (abstract method) are un argument:
<?php
abstract class ParentClass {
// Metoda abstractă (abstract method)cu un argument
abstract protected function prefixName($name);
}
class ChildClass extends ParentClass {
public function prefixName($name) {
if ($name == "Ion Popescu") {
$prefix = "Mr.";
} elseif ($name == "Ioana Popescu") {
$prefix = "Mrs.";
} else {
$prefix = "";
}
return "{$prefix} {$name}";
}
}
$class = new ChildClass;
echo $class->prefixName("Ion Popescu");
echo "<br>";
echo $class->prefixName("Ioana Popescu");
?>
<?php
abstract class ParentClass {
// Metoda abstractă (abstract method) cu un argument
abstract protected function prefixName($name);
}
class ChildClass extends ParentClass {
// Clasa copil (child class) poate defini argumente opționale care nu sunt în metoda abstractă a părintelui (parent's abstract method)
public function prefixName($name, $separator = ".", $greet = "Dear") {
if ($name == "Ion Popescu") {
$prefix = "Mr";
} elseif ($name == "Ioana Popescu") {
$prefix = "Mrs";
} else {
$prefix = "";
}
return "{$greet} {$prefix}{$separator} {$name}";
}
}
$class = new ChildClass;
echo $class->prefixName("Ion Popescu");
echo "<br>";
echo $class->prefixName("Ioana Popescu");
?>
PHP OOP - Trăsături
PHP OOP - Trăsături (PHP OOP - Traits)
PHP - Ce sunt trăsăturile? (PHP - What are Traits?)
PHP acceptă numai moștenirea unică (single inheritance): o clasă copil (child class) poate moșteni doar de la un singur părinte (parent).
Deci, dacă o clasă trebuie să moștenească mai multe comportamente? Trăsăturile OOP (OOP traits) rezolvă această problemă.
Trăsăturile (Traits) sunt utilizate pentru a declara metode care pot fi utilizate în mai multe clase. Trăsăturile pot avea metode (methods) și metode abstracte (abstract methods) care pot fi utilizate în mai multe clase, iar metodele (methods) pot avea orice modificator access (public, privat sau protejat).
Trăsăturile (Traits) sunt declarate cu ajutorul cuvântului cheie trait (trait keyword):
Sintaxă
<?php
trait TraitName {
// ceva cod...
}
?>
Pentru a utiliza o trăsătură (trait) într-o clasă, utilizați cuvântul cheie de utilizare (use keyword):
<?php
class MyClass {
use TraitName;
}
?>
Să ne uităm la un exemplu:
<?php
trait message1 {
public function msg1() {
echo "OOP este distractiv! ";
}
}
class Welcome {
use message1;
}
$obj = new Welcome();
$obj->msg1();
?>
Exemplu explicat
Aici, declarăm o singură trăsătură (trait): message1. Apoi, creem o clasă: Welcome. Clasa utilizează trăsătura (trait) și toate metodele (methods) din trăsătură (trait) vor fi disponibile în clasă.
Dacă alte clase trebuie să utilizeze funcția msg1(), pur și simplu folosiți trăsătura (trait) message1 din acele clase. Acest lucru reduce duplicarea codului, deoarece nu este nevoie să redeclarați din nou aceeași metodă (method).
PHP - Folosirea mai multor trăsături (traits)
Să ne uităm la un alt exemplu:
<?php
trait message1 {
public function msg1() {
echo "OOP este distractiv! ";
}
}
trait message2 {
public function msg2() {
echo "OOP reduce duplicarea codului!";
}
}
class Welcome {
use message1;
}
class Welcome2 {
use message1, message2;
}
$obj = new Welcome();
$obj->msg1();
echo "<br>";
$obj2 = new Welcome2();
$obj2->msg1();
$obj2->msg2();
?>
Exemplu explicat
Aici, declarăm două trăsături (traits): message1 și message2. Apoi, creăm două clase: Welcome și Welcome2. Prima clasă (Welcome) folosește trăsături (traits) message1, iar cea de-a doua (Welcome2) folosește atât caracteristicile message1 cât și message2 (mai multe trăsături (traits) sunt separate prin virgulă).
PHP OOP - Metode statice
PHP OOP - Metode statice
PHP - Metode statice
Metodele statice (static methods) pot fi apelate direct - fără a crea o instanță a unei clase.
Metodele statice (static methods) sunt declarate cu ajutorul cuvântului cheie static (static keyword):
Sintaxă
<?php
class ClassName {
public static function staticMethod() {
echo "Hello World!";
}
}
?>
Pentru a accesa o metodă statică (static method), folosiți numele clasei (class name), dublul punct (::) și numele metodei (method name):
Sintaxă
ClassName::staticMethod();
<?php
class greeting {
public static function welcome() {
echo "Hello World!";
}
}
// Apelare metoda statică (static method)
greeting::welcome();
?>
Exemplu explicat
Aici, declarăm o metodă statică (static method): welcome(). Apoi, apelăm metodă statică (static method) folosind numele clasei (class name), dublul punct (::) și numele metodei (method name) (fără a crea mai întâi o clasă).
PHP - Mai multe despre metodele statice
O clasă poate avea atât metode statice, cât și nestatice (static and non-static methods). O metodă statică (static method) poate fi accesată dintr-o metodă din aceeași clasă folosind cuvântul cheie self (self keyword) și dublul punct (::):
<?php
class greeting {
public static function welcome() {
echo "Hello World!";
}
public function __construct() {
self::welcome();
}
}
new greeting();
?>
Metodele statice (static methods) pot fi, de asemenea, apelate la metode din alte clase. Pentru a face acest lucru, metoda statică (static method) ar trebui să fie publică:
<?php
class greeting {
public static function welcome() {
echo "Hello World!";
}
}
class SomeOtherClass {
public function message() {
greeting::welcome();
}
}
?>
Pentru a apela o metodă statică (static method) dintr-o clasă copil (child class), utilizați cuvântul cheie părinte (parent keyword) din cadrul clasei copil (child class). Aici, metoda statică (static method) poate fi publică sau protejată.
<?php
class domain {
protected static function getWebsiteName() {
return "lectii-virtuale.ro";
}
}
class domainlv extends domain {
public $websiteName;
public function __construct() {
$this->websiteName = parent::getWebsiteName();
}
}
$domainlv = new domainlv;
echo $domainlv -> websiteName;
?>
PHP OOP - Proprietăți statice
PHP OOP - Proprietăți statice
PHP - Proprietăți statice
Proprietățile statice (static properties) pot fi apelate direct - fără a crea o instanță a unei clase.
Proprietățile statice (static properties) sunt declarate cu ajutorul cuvântului cheie static (static keyword):
Sintaxă
<?php
class ClassName {
public static $staticProp = "lectii-virtuale";
}
?>
Pentru a accesa o proprietate statică, folosiți numele clasei (class name), două puncte duble (::) și numele proprietății (property name):
Sintaxă
ClassName::staticProp;
Să ne uităm la un exemplu:
<?php
class pi {
public static $value = 3.14159;
}
// Obțineți proprietăți statice (static property)
echo pi::$value;
?>
Exemplu explicat
Aici, declarăm o proprietate statică (static property): $value. Apoi, facem echo valoarea proprietății statice folosind numele clasei (class name), două puncte duble (::) și numele proprietății (property name): (fără a crea mai întâi o clasă).
PHP - Mai multe despre proprietățile statice
O clasă poate avea atât proprietăți statice, cât și nestatice (static and non-static properties). O proprietate statică (static property) poate fi accesată dintr-o metodă din aceeași clasă folosind cuvântul cheie self (self keyword) și două puncte duble (::):
<?php
class pi {
public static $value=3.14159;
public function staticValue() {
return self::$value;
}
}
$pi = new pi();
echo $pi->staticValue();
?>
Pentru a apela o proprietate statică (static property) dintr-o clasă copil (child class), utilizați cuvântul cheie părinte (parent keyword) din cadrul clasei copil (child class):
<?php
class pi {
public static $value=3.14159;
}
class x extends pi {
public function xStatic() {
return parent::$value;
}
}
// Obțineți valoarea proprietății statice (static property ) direct prin intermediul clasei copil (child class)
echo x::$value;
// sau obțineți valoarea proprietății statice (static property) prin metoda xStatic() (xStatic() method)
$x = new x();
echo $x->xStatic();
?>
PHP Bază de date MySQL
Bază de date PHP MySQL
Cu PHP, vă puteți conecta la și manipula bazele de date.
MySQL este cel mai popular sistem de baze de date folosit cu PHP.
Ce este MySQL?
MySQL este un sistem de baze de date utilizat pe web
MySQL este un sistem de baze de date care rulează pe un server
MySQL este ideal atât pentru aplicații mici cât și pentru aplicații mari
MySQL este foarte rapid, fiabil și ușor de utilizat
MySQL folosește SQL standard
MySQL compilează pe mai multe platforme
MySQL este gratuit pentru a fi descărcat și utilizat
MySQL este dezvoltat, distribuit și susținut de Oracle Corporation
MySQL poartă numele fiicei cofondatoare Monty Widenius: My
Datele dintr-o bază de date MySQL sunt stocate în tabele. Un tabel este o colecție de date conexe și este format din coloane și rânduri.
Bazele de date sunt utile pentru stocarea informațiilor categoric. O companie poate avea o bază de date cu următoarele tabele:
Angajați, Produse, Clienți, Comenzi (Employees, Products, Customers, Orders)
Sistem de baze de date PHP + MySQL
PHP combinat cu MySQL este cross-platform (puteți dezvolta în Windows și puteți lucra pe o platformă Unix)
Database Queries
Un query este o întrebare sau o solicitare (question or a request).
Putem interoga (query) o bază de date (database) pentru informații specifice și putem returna un set de înregistrări.
Uită-te la următoarea interogare (query) (folosind SQL standard):
SELECT LastName FROM Employees
Interogarea (query) de mai sus selectează toate datele din coloana „LastName” din tabelul „Employees”.
Descărcați baza de date MySQL
Dacă nu aveți un server PHP cu o bază de date MySQL, îl puteți descărca gratuit aici: http://www.mysql.com
Date despre baza de date MySQL
MySQL este sistemul de baze de date standard de facto pentru site-urile web cu volume IMPORTANTE atât de date cât și de utilizatori finali (end-users) (cum ar fi Facebook, Twitter și Wikipedia).
Un alt lucru despre MySQL este că poate fi redus pentru a sprijini aplicațiile bazei de date încorporate.
PHP Conectare la MySQL
PHP Conectează-te la MySQL
PHP 5 și versiunile ulterioare pot lucra cu o bază de date MySQL folosind:
Extensia MySQLi („i” este îmbunătățită)
DPO (Obiecte de date PHP/PHP Data Objects)
Versiunile anterioare de PHP au folosit extensia MySQL. Cu toate acestea, această extindere a fost depășită în 2012.
Ar trebui să folosesc MySQLi sau PDO?
Dacă aveți nevoie de un răspuns scurt, ar fi „Orice dorți”.
Atât MySQLi, cât și PDO au avantajele lor:
PDO va funcționa pe 12 sisteme de baze de date diferite, în timp ce MySQLi va funcționa doar cu baze de date MySQL.
Deci, dacă trebuie să schimbați proiectul pentru a utiliza o altă bază de date, PDO ușurează procesul. Trebuie doar să schimbați șirul de conexiune (connection string) și câteva interogari (queries). Cu MySQLi, va trebui să rescrieți întregul cod - interogările (queries) incluse.
Ambele sunt orientate pe obiecte (object-oriented), dar MySQLi oferă și o API procedurală (procedural API).
Ambele acceptă declarații pregătite (Prepared Statements). Declarațiile pregătite (Prepared Statements) protejează împotriva injecției SQL și sunt foarte importante pentru securitatea aplicațiilor web.
Exemple MySQL atât în MySQLi cât și în sintaxa PDO
Aici și în capitolele următoare vom demonstra trei moduri de a lucra cu PHP și MySQL:
MySQLi (orientat pe obiect/object-oriented)
MySQLi (procedural)
DOP
Instalare MySQLi
Pentru Linux și Windows: Extensia MySQLi este instalată automat în majoritatea cazurilor, atunci când este instalat pachetul mysql php5.
Pentru detalii despre instalare, accesați:
http://php.net/manual/en/mysqli.installation.php
Instalare DPO
Pentru detalii despre instalare, accesați: http://php.net/manual/en/pdo.installation.php
Deschideți o conexiune la MySQL
Înainte de a putea accesa datele din baza de date MySQL, trebuie să ne putem conecta la server:
Exemplu (MySQLi orientat pe obiect/MySQLi Object-Oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
echo "Conectat cu succes";
?>
$connect_error a fost spart până la PHP 5.2.9 și 5.3.0. Dacă trebuie să vă asigurați compatibilitatea cu versiunile PHP înainte de 5.2.9 și 5.3.0, utilizați în schimb următorul cod:
// Verificați conexiunea
if (mysqli_connect_error()) {
die("Conexiunea la baza de date a eșuat: " . mysqli_connect_error());
}
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
echo "Conexiunea s-a realizat cu succes";
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
try {
$conn = new PDO("mysql:host=$servername;dbname=myDB", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
echo "Conectat cu succes";
}
catch(PDOException $e)
{
echo "Conexiune eșuată: " . $e->getMessage();
}
?>
În exemplul PDO de mai sus am specificat și o bază de date (myDB). PDO necesită o bază de date validă pentru a vă conecta. Dacă nu este specificată nicio bază de date, se face o excepție.
Un mare beneficiu al PDO este că are o clasă de excepție pentru a rezolva problemele care pot apărea în interogările noastre de baze de date (database queries). Dacă o excepție este făcută în block-ul try{}, scriptul nu mai este executat și curge direct către primul block catch(){}.
Închideți conexiunea
Conexiunea va fi închisă automat la finalizarea scriptului. Pentru a închide înainte conexiunea, utilizați următoarele:
MySQLi Object-Oriented:
$conn->close();
MySQLi Procedural:
mysqli_close($conn);
PDO:
$conn = null;
PHP Creare bază de date MySQL
PHP Creați o bază de date MySQL
O bază de date constă dintr-una sau mai multe tabele.
Veți avea nevoie de privilegii speciale CREATE pentru a crea sau pentru a șterge o bază de date MySQL.
Creați o bază de date MySQL folosind MySQLi și PDO
Instrucțiunea CREATE DATABASE este utilizată pentru a crea o bază de date în MySQL.
Următoarele exemple creează o bază de date denumită "myDB":
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
// Creați baza de date
$sql = "CREATE DATABASE myDB";
if ($conn->query($sql) === TRUE) {
echo "Baza de date creată cu succes";
} else {
echo "Eroare la crearea bazei de date: " . $conn->error;
}
$conn->close();
?>
Când creați o bază de date nouă, trebuie să specificați doar primele trei argumente pentru obiectul mysqli (nume de server, nume de utilizator și parolă/servername, username and password).
Dacă trebuie să folosiți un port specific, adăugați un șir gol (empty string) pentru argumentul numelui bazei de date (database-name argument), astfel: new mysqli("localhost", "username", "password", "", port)
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
// Creați baza de date
$sql = "CREATE DATABASE myDB";
if (mysqli_query($conn, $sql)) {
echo "Bază de date creată cu succes";
} else {
echo "Eroare la crearea bazei de date: " . mysqli_error($conn);
}
mysqli_close($conn);
?>
Următorul exemplu PDO creează o bază de date denumită "myDBPDO":
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
try {
$conn = new PDO("mysql:host=$servername", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$sql = "CREATE DATABASE myDBPDO";
// utilizați exec() deoarece nu se returnează niciun rezultat
$conn->exec($sql);
echo "Bază de date creată cu succes<br>";
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
Un mare beneficiu al PDO este că are o clasă de excepție pentru a rezolva problemele care pot apărea în interogările noastre de baze de date (database queries). Dacă o excepție este făcută în block-ul try{}, scriptul nu mai este executat și este trimis direct către primul block catch(){}. În block-ul catch de mai sus afișam în echo instrucțiunea SQL și mesajul de eroare generat.
PHP MySQL Creare Tabel
PHP MySQL Create Table
Un tabel de baze de date (database table) are propriul nume unic și este format din coloane și rânduri (columns and rows).
Creați un tabel MySQL folosind MySQLi și PDO
Instrucțiunea CREATE TABLE este utilizată pentru a crea un tabel în MySQL.
Vom crea un tabel numit „MyGuests”, cu cinci coloane: "id", "firstname", "lastname", "email" și "reg_date":
CREATE TABLE MyGuests (
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY,
firstname VARCHAR(30) NOT NULL,
lastname VARCHAR(30) NOT NULL,
email VARCHAR(50),
reg_date TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP
)
Tipul de date (data type) specifică ce tip de date poate conține coloana.
După tipul de date (data type), puteți specifica alte atribute opționale pentru fiecare coloană:
NOT NULL - Fiecare rând (row) trebuie să conțină o valoare pentru acea coloană (column), valorile nule nu sunt permise
Valoarea DEFAULT - Setați o valoare implicită care este adăugată atunci când nu este trecută altă valoare
UNSIGNED - Folosit pentru tipuri de numere, limitează datele stocate la numere pozitive și zero
AUTO INCREMENT - MySQL crește automat valoarea câmpului de fiecare dată când se adaugă o nouă înregistrare
PRIMARY KEY - Folosit pentru identificarea unică a rândurilor dintr-un tabel. Coloana cu setarea PRIMARY KEY este adesea un număr de identificare (ID number) și este adesea folosită cu AUTO_INCREMENT
Fiecare tabel trebuie să aibă o coloană de chei primare (primary key column) (în acest caz: coloana „id”). Valoarea sa trebuie să fie unică pentru fiecare înregistrare din tabel.
Următoarele exemple arată cum se creează tabelul în PHP:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented):
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
// sql pentru a crea tabelul
$sql = "CREATE TABLE MyGuests (
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY,
firstname VARCHAR(30) NOT NULL,
lastname VARCHAR(30) NOT NULL,
email VARCHAR(50),
reg_date TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP
)";
if ($conn->query($sql) === TRUE) {
echo "Tabelul MyGuests creat cu succes";
} else {
echo "Eroare la crearea tabelului: " . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
// sql pentru a crea tabelul
$sql = "CREATE TABLE MyGuests (
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY,
firstname VARCHAR(30) NOT NULL,
lastname VARCHAR(30) NOT NULL,
email VARCHAR(50),
reg_date TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP
)";
if (mysqli_query($conn, $sql)) {
echo "Tabelul MyGuests creat cu succes";
} else {
echo "Eroare la crearea tabelului: " . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
// sql pentru a crea tabelul
$sql = "CREATE TABLE MyGuests (
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY,
firstname VARCHAR(30) NOT NULL,
lastname VARCHAR(30) NOT NULL,
email VARCHAR(50),
reg_date TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP
)";
// utilizați exec() deoarece nu se returnează niciun rezultat
$conn->exec($sql);
echo "Tabelul MyGuests creat cu succes";
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Inserare date
PHP MySQL Inserare date
Inserați date în MySQL folosind MySQLi și PDO
După crearea unei baze de date și a unui tabel, putem începe să adăugăm date în ele.
Iată câteva reguli de sintaxă de urmat:
Interogarea SQL (SQL query) trebuie indicată în PHP
Valorile șirului (string values) din interogarea SQL (SQL query) trebuie menționate
Valorile numerice (numeric values) nu trebuie citate
Nu trebuie menționat cuvântul NULL
Instrucțiunea INSERT INTO este utilizată pentru a adăuga noi înregistrări la un tabel MySQL:
INSERT INTO table_name (column1, column2, column3,...)
VALUES (value1, value2, value3,...)
În capitolul precedent, am creat un tabel gol, numit „MyGuests”, cu cinci coloane: "id", "firstname", "lastname", "email" și "reg_date".
Acum, să umplem tabelul cu date.
Dacă o coloană este AUTO_INCREMENT (cum ar fi coloana „id”) sau TIMESTAMP cu actualizarea implicită a current_timesamp (precum coloana „reg_date”), nu este necesar să fie specificată în interogarea SQL (SQL query); MySQL va adăuga automat valoarea.
Următoarele exemple adaugă o nouă înregistrare la tabelul „MyGuests”:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')";
if ($conn->query($sql) === TRUE) {
echo "Noua înregistrare creată cu succes";
} else {
echo "Eroare: " . $sql . "<br>" . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conectarea a eșuat: " . mysqli_connect_error());
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')";
if (mysqli_query($conn, $sql)) {
echo "Noua înregistrare creată cu succes";
} else {
echo "Eroare: " . $sql . "<br>" . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')";
// utilizați exec() deoarece nu se returnează niciun rezultat
$conn->exec($sql);
echo "Noua înregistrare creată cu succes";
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Obțineți ultimul ID introdus
PHP MySQL Obțineți ultimul ID introdus
Obțineți ID-ul ultimei înregistrări introduse
Dacă efectuăm un INSERT sau UPDATE pe o tabelă cu câmpul AUTO_INCREMENT, putem obține imediat ID-ul ultimei înregistrări introduse / actualizate (inserted/updated ).
În tabelul „MyGuests”, coloana „id” este un câmp AUTO_INCREMENT:
CREATE TABLE MyGuests (
id INT(6) UNSIGNED AUTO_INCREMENT PRIMARY KEY,
firstname VARCHAR(30) NOT NULL,
lastname VARCHAR(30) NOT NULL,
email VARCHAR(50),
reg_date TIMESTAMP DEFAULT CURRENT_TIMESTAMP ON UPDATE CURRENT_TIMESTAMP
)
Următoarele exemple sunt egale cu exemplele din pagina anterioară (PHP Insert Data In MySQL), cu excepția faptului că am adăugat o singură linie de cod pentru a prelua ID-ul ultimei înregistrări introduse. De asemenea, afisam cu echo ultimul ID introdus:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')";
if ($conn->query($sql) === TRUE) {
$last_id = $conn->insert_id;
echo "Noua înregistrare creată cu succes. Ultimul ID inserat este: " . $last_id;
} else {
echo "Eroare: " . $sql . "<br>" . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')";
if (mysqli_query($conn, $sql)) {
$last_id = mysqli_insert_id($conn);
echo "Noua înregistrare creată cu succes. Ultimul ID inserat este: " . $last_id;
} else {
echo "Eroare: " . $sql . "<br>" . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('John', 'Doe', '[email protected]')";
// utilizați exec() deoarece nu se returnează niciun rezultat
$conn->exec($sql);
$last_id = $conn->lastInsertId();
echo "Noua înregistrare creată cu succes. Ultimul ID inserat este: " . $last_id;
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Introduceți mai multe înregistrări
PHP MySQL Introduceți mai multe înregistrări
Inserați mai multe înregistrări în MySQL folosind MySQLi și PDO
Mai multe instrucțiuni SQL trebuie executate cu funcția mysqli_multi_query().
Următoarele exemple adaugă trei înregistrări noi în tabelul „MyGuests”:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]');";
$sql .= "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Maria', 'Gheorghe', '[email protected]');";
$sql .= "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Iulia', 'Filipescu', '[email protected]')";
if ($conn->multi_query($sql) === TRUE) {
echo "Înregistrări noi create cu succes";
} else {
echo "Eroare: " . $sql . "<br>" . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]');";
$sql .= "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Maria', 'Gheorghe', '[email protected]');";
$sql .= "INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Iulia', 'Filipescu', '[email protected]')";
if (mysqli_multi_query($conn, $sql)) {
echo "Înregistrări noi create cu succes";
} else {
echo "Eroare: " . $sql . "<br>" . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
// începeți tranzacția
$conn->beginTransaction();
// declarațiile noastre SQL
$conn->exec("INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Ion', 'Popescu', '[email protected]')");
$conn->exec("INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Maria', 'Gheorghe', '[email protected]')");
$conn->exec("INSERT INTO MyGuests (firstname, lastname, email)
VALUES ('Iulia', 'Filipescu', '[email protected]')");
// commit the transaction
$conn->commit();
echo "Înregistrări noi create cu succes";
}
catch(PDOException $e)
{
// dați înapoi tranzacția dacă ceva a eșuat
$conn->rollback();
echo "Eroare: " . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Declarații pregătite
PHP MySQL Declarații pregătite
Declarațiile pregătite (prepared statements) sunt foarte utile împotriva injecțiilor SQL (SQL injections).
Declarații pregătite și parametri legați
O declarație pregătită (prepared statements) este o caracteristică utilizată pentru a executa aceleași (sau similare) instrucțiuni SQL cu o eficiență ridicată.
Declarațiile pregătite (prepared statements) funcționează astfel:
Pregătiți: Un șablon de instrucțiuni SQL (SQL statement template) este creat și trimis în baza de date. Anumite valori sunt lăsate nespecificate, numite parametri (etichetat (labeled ) "?"). Exemplu: INSERT INTO MyGuests VALUES(?, ?, ?)
Baza de date analizează, compilează și efectuează optimizarea interogării pe șablonul de instrucțiuni SQL (SQL statement template) și stochează rezultatul fără a-l executa
Executați: ulterior, aplicația leagă valorile la parametri, iar baza de date execută instrucțiunea. Aplicația poate executa instrucțiunea ori de câte ori dorește cu valori diferite
Față de executarea directă a instrucțiunilor SQL, instrucțiunile pregătite (prepared statements) au trei avantaje principale:
Instrucțiunile pregătite (prepared statements) reduc timpul de analiză (parsing time), deoarece pregătirea pe interogare se face o singură dată (deși instrucțiunea este executată de mai multe ori)
Parametrii legați (bound parameters) minimizează lățimea de bandă (bandwidth) către server, deoarece trebuie să trimiteți de fiecare dată doar parametrii și nu întreaga interogare (query)
Instrucțiunile pregătite (prepared statements) sunt foarte utile împotriva injecțiilor SQL (SQL injections), deoarece valorile parametrilor, care sunt transmise ulterior folosind un protocol diferit, nu trebuie eliberate corect (correctly escaped). Dacă șablonul de instrucțiune originală (original statement template) nu este derivat de la intrarea externă (external input), nu poate apărea injecția SQL (SQL injection).
Declarații pregătite în MySQLi (Prepared Statements in MySQLi)
Următorul exemplu utilizează instrucțiuni pregătite și parametri legați (prepared statements and bound parameters) în MySQLi:
Exemplu (MySQLi cu declarații pregătite/MySQLi with Prepared Statements)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
// pregătiți și legați
$stmt = $conn->prepare("INSERT INTO MyGuests (firstname, lastname, email) VALUES (?, ?, ?)");
$stmt->bind_param("sss", $firstname, $lastname, $email);
// setați parametrii și executați
$firstname = "Ion";
$lastname = "Popescu";
$email = "[email protected]";
$stmt->execute();
$firstname = "Maria";
$lastname = "Gheorghe";
$email = "[email protected]";
$stmt->execute();
$firstname = "Iulia";
$lastname = "Filipescu";
$email = "[email protected]";
$stmt->execute();
echo "Înregistrări noi create cu succes";
$stmt->close();
$conn->close();
?>
Linii de cod pentru a explica exemplul precedent:
"INSERT INTO MyGuests (firstname, lastname, email) VALUES (?, ?, ?)"
În SQL-ul nostru, introducem un semn de întrebare (?) unde vrem să înlocuim o valoare întreagă, string, dublă sau blob (integer, string, double or blob).
Apoi, aruncați o privire la funcția bind_param():
$stmt->bind_param("sss", $firstname, $lastname, $email);
Această funcție leagă parametrii la interogarea SQL (SQL query) și îi spune bazei de date care sunt parametrii. Argumentul „sss” listează tipurile de date (types of data) care sunt parametri. Caracterul s spune mysql-ului că parametrul este un șir (string).
Argumentul poate fi unul din următoarele patru tipuri:
i - număr întreg (integer)
d - dublu (double)
s - șir (string)
b - BLOB
Pentru fiecare parametru trebuie să avem una dintre acestea .
Spunând mysql-ului la ce tip de date (type of data) trebuie să se aștepte, reducem la minimum riscul de injecții SQL (SQL injections.).
Dacă dorim să introducem date din surse externe (cum ar fi intrarea utilizatorului (user input)), este foarte important ca datele să fie igienizate ( sanitized) și validate.
Declarații pregătite în PDO (Prepared Statements in PDO)
Următorul exemplu utilizează declarații pregătite și parametri legați (prepared statements and bound parameters) în PDO:
Exemplu (PDO cu declarații pregătite)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
// pregătiți parametrii sql și bind
$stmt = $conn->prepare("INSERT INTO MyGuests (firstname, lastname, email)
VALUES (:firstname, :lastname, :email)");
$stmt->bindParam(':firstname', $firstname);
$stmt->bindParam(':lastname', $lastname);
$stmt->bindParam(':email', $email);
// introduceți un rând
$firstname = "Ion";
$lastname = "Popescu";
$email = "[email protected]";
$stmt->execute();
// introduceți un alt rând
$firstname = "Maria";
$lastname = "Gheorghe";
$email = "[email protected]";
$stmt->execute();
// introduceți un alt rând
$firstname = "Iulia";
$lastname = "Filipescu";
$email = "[email protected]";
$stmt->execute();
echo "Înregistrări noi create cu succes";
}
catch(PDOException $e)
{
echo "Eroare: " . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Select Data
PHP MySQL Select Data
Selectați datele dintr-o bază de date MySQL
Instrucțiunea SELECT este utilizată pentru a selecta datele dintr-una sau mai multe tabele:
SELECT column_name(s) FROM table_name
sau putem folosi caracterul * pentru a selecta TOATE coloanele dintr-un tabel:
SELECT * FROM table_name
Selectați date cu MySQLi
Selectați date cu MySQLi
Următorul exemplu selectează coloanele id, prenume și nume (id, firstname, lastname) din tabelul MyGuests și îl afișează pe pagină:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
// date de ieșire ale fiecărui rând (output data of each row)
while($row = $result->fetch_assoc()) {
echo "id: " . $row["id"]. " - Name: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
$conn->close();
?>
Linii de cod pentru a explica exemplul de mai sus:
Mai întâi, am configurat o interogare SQL (SQL query) care selectează coloanele id, nume și prenume (id, firstname, lastname) din tabelul MyGuests. Următoarea linie de cod rulează interogarea (query) și pune datele rezultate într-o variabilă numită $result.
Apoi, funcția num_rows() verifică dacă au fost returnate mai mult de zero rânduri.
Dacă sunt returnate mai mult de zero rânduri, funcția fetch_assoc() plasează toate rezultatele într-un tablou asociativ (associative array) pe care îl putem bucla (loop). Bucla (loop) while() buclează setul de rezultate și emite datele din coloanele id, nume și prenume (id, firstname, lastname).
Următorul exemplu arată același lucru ca și exemplul precedent, în modul procedural MySQLi:
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "SELECT id, firstname, lastname FROM MyGuests";
$result = mysqli_query($conn, $sql);
if (mysqli_num_rows($result) > 0) {
// date de ieșire ale fiecărui rând
while($row = mysqli_fetch_assoc($result)) {
echo "id: " . $row["id"]. " - Name: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
mysqli_close($conn);
?>
Puteți pune rezultatul într-un tabel HTML:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
echo "<table><tr><th>ID</th><th>Nume</th></tr>";
// date de ieșire ale fiecărui rând
while($row = $result->fetch_assoc()) {
echo "<tr><td>".$row["id"]."</td><td>".$row["firstname"]." ".$row["lastname"]."</td></tr>";
}
echo "</table>";
} else {
echo "0 results";
}
$conn->close();
?>
Selectați datele cu PDO (+ declarații pregătite/prepared statements)
Următorul exemplu folosește instrucțiuni pregătite (prepared statements).
Selectează coloanele id, prenume și nume (id, firstname, lastname) din tabelul MyGuests și îl afișează într-un tabel HTML:
Exemplu (PDO)
<?php
echo "<table style='border: solid 1px black;'>";
echo "<tr><th>Id</th><th>Prenume</th><th>Nume</th></tr>";
class TableRows extends RecursiveIteratorIterator {
function __construct($it) {
parent::__construct($it, self::LEAVES_ONLY);
}
function current() {
return "<td style='width:150px;border:1px solid black;'>" . parent::current(). "</td>";
}
function beginChildren() {
echo "<tr>";
}
function endChildren() {
echo "</tr>" . "\n";
}
}
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$stmt = $conn->prepare("SELECT id, firstname, lastname FROM MyGuests");
$stmt->execute();
// setați tabloul rezultat la asociativ (set the resulting array to associative)
$result = $stmt->setFetchMode(PDO::FETCH_ASSOC);
foreach(new TableRows(new RecursiveArrayIterator($stmt->fetchAll())) as $k=>$v) {
echo $v;
}
}
catch(PDOException $e) {
echo "Eroare: " . $e->getMessage();
}
$conn = null;
echo "</table>";
?>
PHP MySQL WHERE
PHP MySQL Utilizați clauza WHERE
Selectați și filtrați datele dintr-o bază de date MySQL
Clauza WHERE este folosită pentru a filtra înregistrările.
Clauza WHERE este utilizată pentru a extrage doar acele înregistrări care îndeplinesc o condiție specificată.
SELECT column_name(s) FROM table_name WHERE column_name operator value
Selectați și filtrați datele cu MySQLi
Următorul exemplu selectează coloanele id, prenumele și numele (id, firstname, lastname) din tabelul MyGuests unde numele de familie (lastname) este "Popescu" și îl afișează pe pagina:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests WHERE lastname='Popescu'";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
// date de ieșire ale fiecărui rând
while($row = $result->fetch_assoc()) {
echo "id: " . $row["id"]. " - Nume: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
$conn->close();
?>
Linii de cod pentru a explica exemplul de mai sus:
Mai întâi, am configurat interogarea SQL (SQL query) care selectează coloanele id, prenumele și numele (id, firstname, lastname) din tabelul MyGuests unde numele de familie (lastname) este „Popescu”. Următoarea linie de cod rulează interogarea (query) și pune datele rezultate într-o variabilă numită $result.
Apoi, funcția num_rows() verifică dacă au fost returnate mai mult de zero rânduri.
Dacă sunt returnate mai mult de zero rânduri, funcția fetch_assoc() plasează toate rezultatele într-un tablou asociativ (associative array) pe care îl putem bucla (loop). Bucla (loop) while() buclează setul de rezultate și emite datele din coloanele id, nume și prenume (id, firstname, lastname).
Următorul exemplu arată același lucru ca și exemplul dprecedent, în modul procedural MySQLi:
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "SELECT id, firstname, lastname FROM MyGuests WHERE lastname='Popescu'";
$result = mysqli_query($conn, $sql);
if (mysqli_num_rows($result) > 0) {
// date de ieșire ale fiecărui rând
while($row = mysqli_fetch_assoc($result)) {
echo "id: " . $row["id"]. " - Nume: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
mysqli_close($conn);
?>
Puteți pune rezultatul într-un tabel HTML:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests WHERE lastname='Popescu'";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
echo "<table><tr><th>ID</th><th>Nume</th></tr>";
// date de ieșire ale fiecărui rând
while($row = $result->fetch_assoc()) {
echo "<tr><td>".$row["id"]."</td><td>".$row["firstname"]." ".$row["lastname"]."</td></tr>";
}
echo "</table>";
} else {
echo "0 results";
}
$conn->close();
?>
Selectați date cu PDO (+ declarații pregătite/prepared statements)
Următorul exemplu folosește instrucțiuni pregătite (prepared statements).
Selectează coloanele id, prenumele și numele (id, firstname, lastname) din tabelul MyGuests unde numele de familie este "Popescu" și îl afișează într-un tabel HTML:
Exemplu (PDO)
<?php
echo "<table style='border: solid 1px black;'>";
echo "<tr><th>Id</th><th>Prenume</th><th>Nume</th></tr>";
class TableRows extends RecursiveIteratorIterator {
function __construct($it) {
parent::__construct($it, self::LEAVES_ONLY);
}
function current() {
return "<td style='width:150px;border:1px solid black;'>" . parent::current(). "</td>";
}
function beginChildren() {
echo "<tr>";
}
function endChildren() {
echo "</tr>" . "\n";
}
}
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$stmt = $conn->prepare("SELECT id, firstname, lastname FROM MyGuests WHERE lastname='Popescu'");
$stmt->execute();
// setați tabloul rezultat la asociativ (set the resulting array to associative)
$result = $stmt->setFetchMode(PDO::FETCH_ASSOC);
foreach(new TableRows(new RecursiveArrayIterator($stmt->fetchAll())) as $k=>$v) {
echo $v;
}
}
catch(PDOException $e) {
echo "Eroare: " . $e->getMessage();
}
$conn = null;
echo "</table>";
?>
PHP MySQL ORDER BY
PHP MySQL Utilizați clauza ORDER BY
Selectați și comandați date dintr-o bază de date MySQL (Select and Order Data From a MySQL Database)
Clauza ORDER BY este folosită pentru a sorta setul de rezultate în ordine crescătoare sau descrescătoare.
Clauza ORDER BY sortează înregistrările în ordine crescătoare în mod implicit. Pentru a sorta înregistrările în ordine descrescătoare, utilizați cuvântul cheie DESC.
SELECT column_name(s) FROM table_name ORDER BY column_name(s) ASC|DESC
Selectați și comandați date cu MySQLi (Select and Order Data With MySQLi)
Următorul exemplu selectează coloanele id, prenume și nume (id, firstname, lastname) din tabelul MyGuests. Înregistrările vor fi ordonate după coloana prenumelui:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests ORDER BY lastname";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
// date de ieșire ale fiecărui rând
while($row = $result->fetch_assoc()) {
echo "id: " . $row["id"]. " - Nume: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
$conn->close();
?>
Linii de cod pentru a explica exemplul de mai sus:
În primul rând, am configurat interogarea SQL (SQL query) care selectează coloanele id, prenume și nume (id, firstname, lastname) din tabelul MyGuests. Înregistrările vor fi comandate de coloana cu numele de familie. Următoarea linie de cod rulează interogarea (query) și pune datele rezultate într-o variabilă numită $result.
Apoi, funcția num_rows() verifică dacă au fost returnate mai mult de zero rânduri.
Dacă sunt returnate mai mult de zero rânduri, funcția fetch_assoc() plasează toate rezultatele într-un tablou asociativ (associative array) pe care îl putem bucla (loop). Bucla (loop) while() buclează setul de rezultate și emite datele din coloanele id, prenume și nume (id, firstname, lastname).
Următorul exemplu arată același lucru ca și exemplul precedent, în modul procedural MySQLi:
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "SELECT id, firstname, lastname FROM MyGuests ORDER BY lastname";
$result = mysqli_query($conn, $sql);
if (mysqli_num_rows($result) > 0) {
// date de ieșire ale fiecărui rând
while($row = mysqli_fetch_assoc($result)) {
echo "id: " . $row["id"]. " - Nume: " . $row["firstname"]. " " . $row["lastname"]. "<br>";
}
} else {
echo "0 results";
}
mysqli_close($conn);
?>
Puteți pune rezultatul într-un tabel HTML:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "SELECT id, firstname, lastname FROM MyGuests ORDER BY lastname";
$result = $conn->query($sql);
if ($result->num_rows > 0) {
echo "<table><tr><th>ID</th><th>Nume</th></tr>";
// date de ieșire ale fiecărui rând
while($row = $result->fetch_assoc()) {
echo "<tr><td>".$row["id"]."</td><td>".$row["firstname"]." ".$row["lastname"]."</td></tr>";
}
echo "</table>";
} else {
echo "0 results";
}
$conn->close();
?>
Selectați date cu PDO (+ declarații pregătite/prepared statements)
Următorul exemplu folosește instrucțiuni pregătite (prepared statements).
Aici selectăm coloanele id, prenume și nume (id, firstname, lastname) din tabelul MyGuests. Înregistrările vor fi ordonate după coloana cu numele de familie și vor fi afișate într-un tabel HTML:
Exemplu (PDO)
<?php
echo "<table style='border: solid 1px black;'>";
echo "<tr><th>Id</th><th>Prenume</th><th>Nume</th></tr>";
class TableRows extends RecursiveIteratorIterator {
function __construct($it) {
parent::__construct($it, self::LEAVES_ONLY);
}
function current() {
return "<td style='width:150px;border:1px solid black;'>" . parent::current(). "</td>";
}
function beginChildren() {
echo "<tr>";
}
function endChildren() {
echo "</tr>" . "\n";
}
}
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$stmt = $conn->prepare("SELECT id, firstname, lastname FROM MyGuests ORDER BY lastname");
$stmt->execute();
// setați tabloul rezultat la asociativ (set the resulting array to associative)
$result = $stmt->setFetchMode(PDO::FETCH_ASSOC);
foreach(new TableRows(new RecursiveArrayIterator($stmt->fetchAll())) as $k=>$v) {
echo $v;
}
}
catch(PDOException $e) {
echo "Eroare: " . $e->getMessage();
}
$conn = null;
echo "</table>";
?>
PHP MySQL Delete Data
PHP MySQL Ștergere date
Ștergeți datele dintr-un tabel MySQL folosind MySQLi și PDO
Instrucțiunea DELETE este utilizată pentru a șterge înregistrările dintr-un tabel:
DELETE FROM table_name
WHERE some_column = some_value
Observați clauza WHERE în sintaxa DELETE: clauza WHERE specifică ce înregistrare sau înregistrări trebuie șterse. Dacă omiteți clauza WHERE, toate înregistrările vor fi șterse!
Următoarele exemple șterg înregistrarea cu id=3 din tabelul „MyGuests”:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
// sql pentru a șterge o înregistrare
$sql = "DELETE FROM MyGuests WHERE id=3";
if ($conn->query($sql) === TRUE) {
echo "Înregistrare ștersă cu succes";
} else {
echo "Eroare la ștergerea înregistrării: " . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
// sql pentru a șterge o înregistrare
$sql = "DELETE FROM MyGuests WHERE id=3";
if (mysqli_query($conn, $sql)) {
echo "Înregistrare ștersă cu succes";
} else {
echo "Eroare la ștergerea înregistrării: " . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
// sql pentru a șterge o înregistrare
$sql = "DELETE FROM MyGuests WHERE id=3";
// utilizați exec() deoarece nu se returnează niciun rezultat
$conn->exec($sql);
echo "Înregistrare ștersă cu succes";
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Update Data
PHP MySQL Actualizare date
Actualizarea datelor într-un tabel MySQL folosind MySQLi și PDO
Instrucțiunea UPDATE este utilizată pentru a actualiza înregistrările existente într-un tabel:
UPDATE table_name
SET column1=value, column2=value2,...
WHERE some_column=some_value
Observați clauza WHERE în sintaxa UPDATE: clauza WHERE specifică ce înregistrare sau înregistrări ar trebui actualizate. Dacă omiteți clauza WHERE, toate înregistrările vor fi actualizate!
Următoarele exemple actualizează înregistrarea cu id = 2 în tabelul „MyGuests”:
Exemplu (MySQLi Orientat pe obiect/MySQLi Object-oriented)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = new mysqli($servername, $username, $password, $dbname);
// Verificați conexiunea
if ($conn->connect_error) {
die("Conexiunea a eșuat: " . $conn->connect_error);
}
$sql = "UPDATE MyGuests SET lastname='Popescu' WHERE id=2";
if ($conn->query($sql) === TRUE) {
echo "Înregistrare actualizată cu succes";
} else {
echo "Eroare la actualizarea înregistrării: " . $conn->error;
}
$conn->close();
?>
Exemplu (MySQLi Procedural)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDB";
// Creați conexiunea
$conn = mysqli_connect($servername, $username, $password, $dbname);
// Verificați conexiunea
if (!$conn) {
die("Conexiunea a eșuat: " . mysqli_connect_error());
}
$sql = "UPDATE MyGuests SET lastname='Popescu' WHERE id=2";
if (mysqli_query($conn, $sql)) {
echo "Înregistrare actualizată cu succes";
} else {
echo "Eroare la actualizarea înregistrării: " . mysqli_error($conn);
}
mysqli_close($conn);
?>
Exemplu (PDO)
<?php
$servername = "localhost";
$username = "username";
$password = "password";
$dbname = "myDBPDO";
try {
$conn = new PDO("mysql:host=$servername;dbname=$dbname", $username, $password);
// setați modul de eroare PDO la excepție
$conn->setAttribute(PDO::ATTR_ERRMODE, PDO::ERRMODE_EXCEPTION);
$sql = "UPDATE MyGuests SET lastname='Popescu' WHERE id=2";
// Pregătirea declarației (statement)
$stmt = $conn->prepare($sql);
// executați interogarea (query)
$stmt->execute();
// echo un mesaj pentru a spune că UPDATE a reușit
echo $stmt->rowCount() . " records UPDATED successfully";
}
catch(PDOException $e)
{
echo $sql . "<br>" . $e->getMessage();
}
$conn = null;
?>
PHP MySQL Limit Data
PHP MySQL Limitarea selecțiilor de date
Limitați selecțiile de date dintr-o bază de date MySQL
MySQL oferă o clauză LIMIT care este utilizată pentru a specifica numărul de înregistrări de returnat.
Clauza LIMIT facilitează codarea rezultatelor pe mai multe pagini sau paginarea cu SQL și este foarte utilă pe tabelele mari. Returnarea unui număr mare de înregistrări poate avea impact asupra performanței.
Presupunem că dorim să selectăm toate înregistrările de la 1 la 30 (inclusiv) dintr-un tabel numit „Comenzi” (Orders). Interogarea SQL ar arăta astfel:
$sql = "SELECT * FROM Orders LIMIT 30";
Când se execută interogarea SQL (SQL query) de mai sus, aceasta va returna primele 30 de înregistrări.
Ce se întâmplă dacă vrem să selectăm înregistrările 16 - 25 (inclusiv)?
Mysql oferă, de asemenea, o modalitate de a face acest lucru: folosind OFFSET.
Interogarea SQL (SQL query) de mai jos spune „returnează doar 10 înregistrări, începeți la înregistrarea 16 (OFFSET 15)”:
$sql = "SELECT * FROM Orders LIMIT 10 OFFSET 15";
Puteți utiliza, de asemenea, o sintaxă mai scurtă pentru a obține același rezultat:
$sql = "SELECT * FROM Orders LIMIT 15, 10";
Rețineți că numerele sunt inversate atunci când utilizați o virgulă.
PHP XML Parsers
PHP XML Parsers
Ce este XML?
Limbajul XML este o modalitate de structurare a datelor pentru partajarea pe site-uri web.
Mai multe tehnologii web precum RSS Feed și Podcast-uri sunt scrise în XML.
XML este ușor de creat. Seamănă foarte mult cu HTML, cu excepția faptului că vă alcătuiți propriile etichete.
Ce este un parser XML?
Pentru a citi și actualiza, crea și manipula (read and update, create and manipulate) un document XML, veți avea nevoie de un analizator (parser) XML.
În PHP există două tipuri majore de analizoare (parsers) XML:
Tree-Based Parsers
Event-Based Parsers
Tree-Based Parsers
Analizatorii pe baza de arbori (Tree-Based Parsers) dețin întregul document în memorie și transformă documentul XML într-o structură Tree. Analizează întregul document și oferă acces la elementele Tree (DOM).
Acest tip de analizor (type of parser) este o opțiune mai bună pentru documentele XML mai mici, dar nu pentru documentele XML mari, deoarece provoacă probleme majore de performanță.
Exemplu de analizatori pe baza de arbori (tree-based parsers):
SimpleXML
DOM
Event-Based Parsers
Analizatorii pe bază de evenimente (Event-Based Parsers) nu dețin întregul document în memorie, ci citesc într-un singur nod simultan și vă permit să interacționați în timp real. Odată ce treceți pe următorul nod, cel vechi este aruncat.
Acest tip de analizator (type of parser) este potrivit pentru documentele XML mari. Acesta analizează mai repede și consumă mai puțină memorie.
Exemplu de analizatoare bazate pe evenimente (Event-Based Parsers):
XMLReader
XML Expat Parser
PHP SimpleXML Parser
PHP SimpleXML Parser
SimpleXML este o extensie PHP care ne permite să manipulăm cu ușurință și să obținem date XML.
Parserul SimpleXML
SimpleXML este un analizator bazat pe arbori (tree-based parser).
SimpleXML oferă o modalitate ușoară de a obține numele, atributele și conținutul textului unui element (name, attributes and textual content), dacă știți structura sau aspectul (layout) documentului XML.
SimpleXML transformă un document XML într-o structură de date (data structure ) pe care o puteți repeta printr-o colecție de tablouri (collection of arrays) și obiecte.
În comparație cu DOM sau analizatorul (parser) Expat, SimpleXML ia mai puține linii de cod pentru a citi datele text dintr-un element.
Instalare
De la PHP 5, funcțiile SimpleXML fac parte din nucleul PHP. Nu este necesară instalarea pentru a utiliza aceste funcții.
PHP SimpleXML - Citiți din șir (string)
Funcția PHP simplexml_load_string() este utilizată pentru a citi datele XML dintr-un șir (string).
Presupunem că avem o variabilă care conține date XML, astfel:
$myXMLData =
"<?xml version='1.0' encoding='UTF-8'?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>";
Exemplul de mai jos arată cum să utilizați funcția simplexml_load_string() pentru a citi datele XML dintr-un șir (string):
<?php
$myXMLData =
"<?xml version='1.0' encoding='UTF-8'?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>";
$xml=simplexml_load_string($myXMLData) or die("Eroare: Nu se poate crea obiectul");
print_r($xml);
?>
Rezultatul codului de mai sus va fi:
SimpleXMLElement Object ( [to] => Popescu [from] => Ioana [heading] => Reminder [body] => Nu uitați de mine în acest weekend! )
Utilizați funcționalitatea libxml pentru a prelua toate erorile XML la încărcarea documentului și apoi repetați erorile.
Următorul exemplu încearcă să încarce un șir (string) XML rupt:
<?php
libxml_use_internal_errors(true);
$myXMLData =
"<?xml version='1.0' encoding='UTF-8'?>
<document>
<user>Ion Popescu</wronguser>
<email>[email protected]</wrongemail>
</document>";
$xml = simplexml_load_string($myXMLData);
if ($xml === false) {
echo "Încărcarea XML a eșuat: ";
foreach(libxml_get_errors() as $error) {
echo "<br>", $error->message;
}
} else {
print_r($xml);
}
?>
Încărcarea XML a eșuat:
Nepotrivirea etichetelor de deschidere și incheiere (opening și ending) : linia de utilizator 3 și utilizator greșit (user line 3 and wronguser)
Nepotrivirea etichetelor de deschidere și incheiere (opening și ending): linia de e-mail 4 și e-mail greșit (email line 4 and wrongemail)
PHP SimpleXML - Citiți din fișier (Read From File)
Funcția PHP simplexml_load_file() este utilizată pentru a citi datele XML dintr-un fișier.
Presupunem că avem un fișier XML numit "note.xml", care arată astfel:
<?xml version="1.0" encoding="UTF-8"?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>
Exemplul de mai jos arată cum să utilizați funcția simplexml_load_file() pentru a citi datele XML dintr-un fișier:
<?php
$xml=simplexml_load_file("note.xml") or die("Eroare: Nu se poate crea obiectul");
print_r($xml);
?>
Rezultatul codului de mai sus va fi:
SimpleXMLElement Object ( [to] => Popescu [from] => Ioana [heading] => Reminder [body] => Nu uitați de mine în acest weekend! )
Capitolul următor arată cum să obțineți/recuperați valorile nodului (get/retrieve node values) dintr-un fișier XML cu SimpleXML!
PHP SimpleXML - Obțineți valorile nod/atribut
PHP SimpleXML - Obțineți valorile nod/atribut (Get Node/Attribute Values)
SimpleXML este o extensie PHP care ne permite să manipulăm cu ușurință și să obținem date XML.
PHP SimpleXML - Obțineți valorile nodului (Get Node Values)
Obțineți valorile nodului din fișierul „note.xml”:
<?php
$xml=simplexml_load_file("note.xml") or die("Eroare: Nu se poate crea obiectul");
echo $xml->to . "<br>";
echo $xml->from . "<br>";
echo $xml->heading . "<br>";
echo $xml->body;
?>
Rezultatul codului de mai sus va fi:
Ioana
Popescu
Reminder
Nu uita de mine în acest weekend!
Un alt fișier XML
Presupunem că avem un fișier XML numit "books.xml", care arată astfel:
<?xml version="1.0" encoding="utf-8"?>
<bookstore>
<book category="COOKING">
<title lang="en">Everyday Italian</title>
<author>Giada De Laurentiis</author>
<year>2005</year>
<price>30.00</price>
</book>
<book category="CHILDREN">
<title lang="en">Harry Potter</title>
<author>J K. Rowling</author>
<year>2005</year>
<price>29.99</price>
</book>
<book category="WEB">
<title lang="en-us">XQuery Kick Start</title>
<author>James McGovern</author>
<year>2003</year>
<price>49.99</price>
</book>
<book category="WEB">
<title lang="en-us">Learning XML</title>
<author>Erik T. Ray</author>
<year>2003</year>
<price>39.95</price>
</book>
</bookstore>
PHP SimpleXML - Obțineți valorile de nod ale unor elemente specifice (Get Node Values of Specific Elements)
Următorul exemplu obține valoarea nodului elementului <title> din primul și al doilea element <book> din fișierul "books.xml":
<?php
$xml=simplexml_load_file("books.xml") or die("Eroare: Nu se poate crea obiectul");
echo $xml->book[0]->title . "<br>";
echo $xml->book[1]->title;
?>
Rezultatul codului de mai sus va fi:
Everyday Italian
Harry Potter
PHP SimpleXML - Obțineți valorile nodului - Buclă (Get Node Values - Loop)
Următorul exemplu buclează (loops) toate elementele <book> din fișierul "books.xml" și primește valorile nodurilor ale elementelor <title>, <author>, <year> și <price>:
<?php
$xml=simplexml_load_file("books.xml") or die("Eroare: Nu se poate crea obiectul");
foreach($xml->children() as $books) {
echo $books->title . ", ";
echo $books->author . ", ";
echo $books->year . ", ";
echo $books->price . "<br>";
}
?>
Rezultatul codului de mai sus va fi:
Everyday Italian, Giada De Laurentiis, 2005, 30.00
Harry Potter, J K. Rowling, 2005, 29.99
XQuery Kick Start, James McGovern, 2003, 49.99
Learning XML, Erik T. Ray, 2003, 39.95
PHP SimpleXML - Obțineți valorile atributului (Get Attribute Values)
Următorul exemplu obține valoarea atributului ale atributului „category” al primului element <book> și valoarea atributului a atributului „lang” al elementului <title> din al doilea element <book>:
<?php
$xml=simplexml_load_file("books.xml") or die("Eroare: Nu se poate crea obiectul");
echo $xml->book[0]['category'] . "<br>";
echo $xml->book[1]->title['lang'];
?>
Rezultatul codului de mai sus va fi:
COOKING
en
PHP SimpleXML - Obțineți valorile atributului - Buclă (Get Attribute Values - Loop)
Următorul exemplu obține valorile atributelor elementelor <title> din fișierul "books.xml":
<?php
$xml=simplexml_load_file("books.xml") or die("Eroare: Nu se poate crea obiectul");
foreach($xml->children() as $books) {
echo $books->title['lang'];
echo "<br>";
}
?>
Rezultatul codului de mai sus va fi:
en
en
en-us
en-us
PHP XML Expat Parser
PHP XML Expat Parser
Analizatorul (parser) XML Expat integrat permite procesarea documentelor XML în PHP.
Analizatorul (parser) XML Expat
Analizatorul (parser) Expat este un analizator (parser) bazat pe evenimente.
Priviți următoarea fracție XML:
<from>Ioana</from>
Un analizator bazat pe evenimente (event-based parser) raportează XML-ul de mai sus ca o serie de trei evenimente:
Start element: from
Start CDATA section, value: Ioana
Close element: from
Funcțiile XML Expat Parser fac parte din nucleul PHP. Nu este necesară instalarea pentru a utiliza aceste funcții.
Fișierul XML
Fișierul XML „note.xml” va fi utilizat în exemplul de mai jos:
<?xml version="1.0" encoding="UTF-8"?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>
Inițializarea analizatorului XML Expat (XML Expat Parser)
Vrem să inițializăm XML Expat Parser în PHP, să definim unii manageri pentru diferite evenimente XML, apoi să analizăm fișierul XML.
<?php
// Inițializați analizatorul XML (XML parser)
$parser=xml_parser_create();
// Funcție de utilizat la începutul unui element
function start($parser,$element_name,$element_attrs) {
switch($element_name) {
case "NOTE":
echo "-- Note --<br>";
break;
case "TO":
echo "To: ";
break;
case "FROM":
echo "From: ";
break;
case "HEADING":
echo "Heading: ";
break;
case "BODY":
echo "Message: ";
}
}
// Funcție de utilizat la sfârșitul unui element
function stop($parser,$element_name) {
echo "<br>";
}
// Funcție de utilizat la găsirea datelor de tip caracter
function char($parser,$data) {
echo $data;
}
// Specificați elementul handler
xml_set_element_handler($parser,"start","stop");
// Specificați gestionarul de date (data handler)
xml_set_character_data_handler($parser,"char");
// Deschideți fișierul XML
$fp=fopen("note.xml","r");
// Citiți datele
while ($data=fread($fp,4096)) {
xml_parse($parser,$data,feof($fp)) or
die (sprintf("XML Error: %s at line %d",
xml_error_string(xml_get_error_code($parser)),
xml_get_current_line_number($parser)));
}
// Eliberați analizatorul XML (XML parser)
xml_parser_free($parser);
?>
PHP XML DOM Parser
PHP XML DOM Parser
Analizatorul DOM încorporat (built-in DOM parser) face posibilă procesarea documentelor XML în PHP.
Analizatorul XML DOM
Analizatorul DOM (DOM parser) este un analizator bazat pe arbori (tree-based parser).
Priviți următoarea fracție document XML (XML document fraction):
<?xml version="1.0" encoding="UTF-8"?>
<from>Ioana</from>
DOM vede XML-ul de mai sus ca o structură de arbore (tree structure):
Nivelul 1: Document XML
Nivelul 2: Elementul rădăcină: <de la>
Nivelul 3: Element text: "Ioana"
Instalare
Funcțiile analizatorului DOM (DOM parser) fac parte din nucleul PHP. Nu este necesară instalarea pentru a utiliza aceste funcții.
Fișierul XML
Fișierul XML de mai jos („note.xml”) va fi utilizat în exemplul nostru:
<?xml version="1.0" encoding="UTF-8"?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>
XML de încărcare și ieșire (Load and Output XML)
Vrem să inițializăm analizatorul XML (XML parser), să încărcăm xml-ul și să îl scoatem:
<?php
$xmlDoc = new DOMDocument();
$xmlDoc->load("note.xml");
print $xmlDoc->saveXML();
?>
Rezultatul codului de mai sus va fi:
Popescu Ioana Reminder Nu uita de mine în acest weekend!
Dacă selectați „View source” în fereastra browserului, veți vedea următorul HTML:
<?xml version="1.0" encoding="UTF-8"?>
<note>
<to>Popescu</to>
<from>Ioana</from>
<heading>Reminder</heading>
<body>Nu uitați de mine în acest weekend!</body>
</note>
Buclă prin XML (Looping through XML)
Vrem să inițializăm analizatorul XML, să încărcăm XML și să ne buclăm (loop) prin toate elementele elementului <note>:
<?php
$xmlDoc = new DOMDocument();
$xmlDoc->load("note.xml");
$x = $xmlDoc->documentElement;
foreach ($x->childNodes AS $item) {
print $item->nodeName . " = " . $item->nodeValue . "<br>";
}
?>
Rezultatul codului de mai sus va fi:
#text =
to = Popescu
#text =
from = Ioana
#text =
heading = Reminder
#text =
body = Nu ma uita in acest weekend!
#text =
În exemplul de mai sus vedeți că există noduri de text goale (empty text nodes) între fiecare element.
Când XML generează, conține adesea spații albe (white-spaces) între noduri. Analizatorul XML DOM (XML DOM parser) tratează acestea ca elemente obișnuite și, dacă nu sunteți conștienți de ele, uneori provoacă probleme.
PHP - AJAX Introducere
PHP - AJAX Introducere
AJAX este despre actualizarea părților unei pagini web, fără a reîncărca întreaga pagină.
Ce este AJAX?
AJAX = JavaScript asincron și XML.
AJAX este o tehnică pentru crearea de pagini web rapide și dinamice.
AJAX permite actualizarea asincronă a paginilor web, schimbând cantități mici de date cu serverul din culise. Aceasta înseamnă că este posibil să actualizați părți ale unei pagini web, fără a reîncărca întreaga pagină.
Paginile web clasice (care nu utilizează AJAX) trebuie să reîncarce întreaga pagină dacă conținutul ar trebui să se schimbe.
Exemple de aplicații care utilizează AJAX: Google Maps, Gmail, Youtube și Facebook.
AJAX se bazează pe standardele de internet
AJAX se bazează pe standardele de internet și folosește o combinație de:
Obiectul XMLHttpRequest (pentru schimbul de date asincron cu un server)
JavaScript / DOM (pentru afișarea / interacțiunea cu informațiile)
CSS (pentru stilizarea datelor)
XML (adesea folosit ca format pentru transferul de date)
Aplicațiile AJAX sunt independente de browser și de platformă!
Sugestie Google
AJAX a fost popularizat în 2005 de Google, cu Google Suggest.
Google Suggest utilizează AJAX pentru a crea o interfață web foarte dinamică: Când începeți să tastați în caseta de căutare Google, un JavaScript trimite cererea de informații pe un server și serverul returnează o listă de sugestii.
Începeți să utilizați AJAX Today
În tutorialul nostru PHP, vom demonstra modul în care AJAX poate actualiza părți ale unei pagini web, fără a reîncărca întreaga pagină. Scriptul serverului va fi scris în PHP.
PHP AJAX
PHP - AJAX și PHP
AJAX este utilizat pentru a crea mai multe aplicații interactive.
Exemplu AJAX PHP
Următorul exemplu va demonstra modul în care o pagină web poate comunica cu un server web în timp ce un utilizator tastează într-un câmp de intrare (input field).
Când un utilizator introduce un caracter în câmpul de intrare (input field), se execută o funcție numită "showHint()".
Funcția este declanșată de evenimentul onkeyup.
<html>
<head>
<script>
function showHint(str) {
if (str.length == 0) {
document.getElementById("txtHint").innerHTML = "";
return;
} else {
var xmlhttp = new XMLHttpRequest();
xmlhttp.onreadystatechange = function() {
if (this.readyState == 4 && this.status == 200) {
document.getElementById("txtHint").innerHTML = this.responseText;
}
};
xmlhttp.open("GET", "gethint.php?q=" + str, true);
xmlhttp.send();
}
}
</script>
</head>
<body>
<p><b>Începeți să tastați un prenume în câmpul de introducere (input field) de mai jos:</b></p>
<form>
Prenume: <input type="text" onkeyup="showHint(this.value)">
</form>
<p>Sugestii: <span id="txtHint"></span></p>
</body>
</html>
Explicarea codului:
În primul rând, verificați dacă câmpul de intrare (input field) este gol (str.length == 0). Dacă este, ștergeți conținutul marcajului de substituție txtHint și ieșiți din funcție.
Cu toate acestea, dacă câmpul de intrare nu este gol, faceți următoarele:
Creați un obiect XMLHttpRequest
Creați funcția care trebuie executată atunci când răspunsul serverului este gata
Trimiteți cererea la un fișier PHP (gethint.php) de pe server
Observați că parametrul q este adăugat la url (gethint.php?q="+str)
Și variabila str conține conținutul câmpului de intrare (input field)
Fișierul PHP - "gethint.php"
Fișierul PHP verifică o serie de nume și returnează numele corespunzător browserului:
<?php
// Array with names
$a[] = "Ana";
$a[] = "Briana";
$a[] = "Cristina";
$a[] = "Diana";
$a[] = "Eva";
$a[] = "Florina";
$a[] = "Gina";
$a[] = "Helena";
$a[] = "Ina";
$a[] = "Jana";
$a[] = "Karina";
$a[] = "Liliana";
$a[] = "Nina";
$a[] = "Ofelia";
$a[] = "Petronela";
$a[] = "Alexandra";
$a[] = "Rahela";
$a[] = "Corina";
$a[] = "Dorina";
$a[] = "Evelina";
$a[] = "Emilia";
$a[] = "Sorina";
$a[] = "Tina";
$a[] = "Luana";
$a[] = "Violeta";
$a[] = "Lizuca";
$a[] = "Elizsabeta";
$a[] = "Eliana";
$a[] = "Wanda";
$a[] = "Victoria;
// obțineți parametrul q de la URL
$q = $_REQUEST["q"];
$hint = "";
// căutarea tuturor indiciilor din tablou (array) dacă $q este diferit de ""
if ($q !== "") {
$q = strtolower($q);
$len=strlen($q);
foreach($a as $name) {
if (stristr($q, substr($name, 0, $len))) {
if ($hint === "") {
$hint = $name;
} else {
$hint .= ", $name";
}
}
}
}
// Ieșirea „fără sugestii” dacă nu a fost găsit niciun indiciu sau ieșirea valorilor corecte
echo $hint === "" ? "nici o sugestie" : $hint;
?>
PHP Bază de date AJAX
PHP - AJAX și MySQL
AJAX poate fi utilizat pentru comunicarea interactivă cu o bază de date.
Exemplu de bază de date AJAX
Modul în care o pagină web poate obține informații dintr-o bază de date cu AJAX:
Exemplu explicat
Când un utilizator selectează o persoană din lista derulantă, se execută o funcție numită „showUser()”.
Funcția este declanșată de evenimentul onchange.
<html>
<head>
<script>
function showUser(str) {
if (str == "") {
document.getElementById("txtHint").innerHTML = "";
return;
} else {
if (window.XMLHttpRequest) {
// code for IE7+, Firefox, Chrome, Opera, Safari
xmlhttp = new XMLHttpRequest();
} else {
// code for IE6, IE5
xmlhttp = new ActiveXObject("Microsoft.XMLHTTP");
}
xmlhttp.onreadystatechange = function() {
if (this.readyState == 4 && this.status == 200) {
document.getElementById("txtHint").innerHTML = this.responseText;
}
};
xmlhttp.open("GET","getuser.php?q="+str,true);
xmlhttp.send();
}
}
</script>
</head>
<body>
<form>
<select name="users" onchange="showUser(this.value)">
<option value="">Select a person:</option>
<option value="1">Petre Georgescu</option>
<option value="2">Luiza Georgescu</option>
<option value="3">Ion Suciu</option>
<option value="4">Georgiana Ionescu</option>
</select>
</form>
<br>
<div id="txtHint"><b>Informațiile despre persoană vor fi enumerate aici ... </b></div>
</body>
</html>
Verificați dacă persoana este selectată. Dacă nu este selectată nicio persoană (str == ""), ștergeți conținutul txtHint și ieșiți din funcție. Dacă este selectată o persoană, faceți următoarele:
Creați un obiect XMLHttpRequest
Creați funcția care trebuie executată atunci când răspunsul serverului este gata
Trimiteți cererea dezactivată unui fișier de pe server
Observați că la URL se adaugă un parametru (q) (avand conținutul listei derulante)
Fișierul PHP
Pagina de pe server numită de JavaScript-ul precedent este un fișier PHP numit "getuser.php".
Codul sursă din „getuser.php” rulează o interogare (query) împotriva unei baze de date MySQL și returnează rezultatul într-un tabel HTML:
<!DOCTYPE html>
<html>
<head>
<style>
table {
width: 100%;
border-collapse: collapse;
}
table, td, th {
border: 1px solid black;
padding: 5px;
}
th {text-align: left;}
</style>
</head>
<body>
<?php
$q = intval($_GET['q']);
$con = mysqli_connect('localhost','petre','abc123','my_db');
if (!$con) {
die('Nu s-a putut conecta: ' . mysqli_error($con));
}
mysqli_select_db($con,"ajax_demo");
$sql="SELECT * FROM user WHERE id = '".$q."'";
$result = mysqli_query($con,$sql);
echo "<table>
<tr>
<th>Prenume</th>
<th>Nume</th>
<th>Vârsta</th>
<th>Orașul natal</th>
<th>Job</th>
</tr>";
while($row = mysqli_fetch_array($result)) {
echo "<tr>";
echo "<td>" . $row['Prenume'] . "</td>";
echo "<td>" . $row['Nume'] . "</td>";
echo "<td>" . $row['Vârsta'] . "</td>";
echo "<td>" . $row['Orașul natal'] . "</td>";
echo "<td>" . $row['Job'] . "</td>";
echo "</tr>";
}
echo "</table>";
mysqli_close($con);
?>
</body>
</html>
Când interogarea este trimisă de la JavaScript în fișierul PHP, se întâmplă următoarele:
PHP deschide o conexiune la un server MySQL
Este găsită persoana corectă
Un tabel HTML este creat, umplut cu date și trimis înapoi la marcatorul de locație (placeholder) „txtHint”
PHP AJAX - XML
PHP - AJAX și XML
AJAX poate fi utilizat pentru comunicarea interactivă cu un fișier XML.
Exemplu AJAX XML
Următorul exemplu va demonstra cum o pagină web poate extrage informații dintr-un fișier XML cu AJAX:
Exemplu explicat - Pagina HTML
Când un utilizator selectează un CD dint-o listă verticală, se execută o funcție numită "showCD()". Funcția este declanșată de evenimentul "onchange":
<html>
<head>
<script>
function showCD(str) {
if (str=="") {
document.getElementById("txtHint").innerHTML="";
return;
}
if (window.XMLHttpRequest) {
// cod pentru IE7+, Firefox, Chrome, Opera, Safari
xmlhttp=new XMLHttpRequest();
} else { // cod pentru IE6, IE5
xmlhttp=new ActiveXObject("Microsoft.XMLHTTP");
}
xmlhttp.onreadystatechange=function() {
if (this.readyState==4 && this.status==200) {
document.getElementById("txtHint").innerHTML=this.responseText;
}
}
xmlhttp.open("GET","getcd.php?q="+str,true);
xmlhttp.send();
}
</script>
</head>
<body>
<form>
Selectați un CD:
<select name="cds" onchange="showCD(this.value)">
<option value="">Selectați un CD:</option>
<option value="Bon Jovi">Bob Dylan</option>
<option value="Beatles">Bee Gees</option>
<option value="Scorpions">Cat Stevens</option>
</select>
</form>
<div id="txtHint"><b>Informațiile despre CD vor fi enumerate aici ... </b></div>
</body>
</html>
Funcția showCD() face următoarele:
Verificați dacă este selectat un CD
Creați un obiect XMLHttpRequest
Creați funcția care trebuie executată atunci când răspunsul serverului este gata
Trimiteți cererea dezactivată unui fișier de pe server
Observați că la URL se adaugă un parametru (q) (cu conținutul listei derulante)
Fișierul PHP
Pagina de pe server numită de JavaScript-ul precedent este un fișier PHP numit "getcd.php".
Scriptul PHP încarcă un document XML, "cd_catalog.xml", rulează o interogare (query) împotriva fișierului XML și returnează rezultatul ca HTML:
<?php
$q=$_GET["q"];
$xmlDoc = new DOMDocument();
$xmlDoc->load("cd_catalog.xml");
$x=$xmlDoc->getElementsByTagName('ARTIST');
for ($i=0; $i<=$x->length-1; $i++) {
//Procesați numai nodurile element
if ($x->item($i)->nodeType==1) {
if ($x->item($i)->childNodes->item(0)->nodeValue == $q) {
$y=($x->item($i)->parentNode);
}
}
}
$cd=($y->childNodes);
for ($i=0;$i<$cd->length;$i++) {
//Procesați numai nodurile element
if ($cd->item($i)->nodeType==1) {
echo("<b>" . $cd->item($i)->nodeName . ":</b> ");
echo($cd->item($i)->childNodes->item(0)->nodeValue);
echo("<br>");
}
}
?>
Când interogarea CD este trimisă de la JavaScript la pagina PHP, se întâmplă următoarele:
PHP creează un obiect XML DOM
Găsiți toate elementele <artist> care se potrivesc cu numele trimis de la JavaScript
Afișați informațiile despre album (trimiteți la marcatorul „txtHint”)
PHP - AJAX Căutare live
PHP - AJAX Căutare live
AJAX poate fi utilizat pentru a crea căutări mai prietenoase și interactive pentru utilizator.
AJAX Căutare live
Următorul exemplu va demonstra o căutare live, unde obțineți rezultate de căutare în timp ce tastați.
Căutarea live are multe avantaje în comparație cu căutarea tradițională:
Rezultatele sunt afișate pe măsură ce tastați
Rezultatele se restrâng pe măsură ce continuați să scrieți
Dacă rezultatele devin prea restrânse, eliminați caracterele pentru a vedea un rezultat mai larg
Rezultatele se găsesc într-un fișier XML (de ex. links.xml). Pentru a face acest exemplu mic și simplu, sunt disponibile doar șase rezultate.
Exemplu explicat - Pagina HTML
Când un utilizator tastează un caracter în câmpul de intrare, funcția „showResult()” este executată. Funcția este declanșată de evenimentul "onkeyup":
<html>
<head>
<script>
function showResult(str) {
if (str.length==0) {
document.getElementById("livesearch").innerHTML="";
document.getElementById("livesearch").style.border="0px";
return;
}
if (window.XMLHttpRequest) {
// cod pentru IE7+, Firefox, Chrome, Opera, Safari
xmlhttp=new XMLHttpRequest();
} else { // cod pentru IE6, IE5
xmlhttp=new ActiveXObject("Microsoft.XMLHTTP");
}
xmlhttp.onreadystatechange=function() {
if (this.readyState==4 && this.status==200) {
document.getElementById("livesearch").innerHTML=this.responseText;
document.getElementById("livesearch").style.border="1px solid #A5ACB2";
}
}
xmlhttp.open("GET","livesearch.php?q="+str,true);
xmlhttp.send();
}
</script>
</head>
<body>
<form>
<input type="text" size="30" onkeyup="showResult(this.value)">
<div id="livesearch"></div>
</form>
</body>
</html>
Explicația codului sursă:
Dacă câmpul de intrare (input field) este gol (str.length == 0), funcția șterge conținutul marcatorului de căutare live (livesearch placeholder) și iese din funcție.
Dacă câmpul de intrare (input field) nu este gol, funcția showResult() execută următoarele:
Creați un obiect XMLHttpRequest
Creați funcția care trebuie executată atunci când răspunsul serverului este gata
Trimiteți cererea dezactivată unui fișier de pe server
Observați că la URL se adaugă un parametru (q) (cu conținutul câmpului de introducere (input field))
Fișierul PHP
Pagina de pe server numită de JavaScript-ul precedent este un fișier PHP numit "livesearch.php".
Codul sursă din „livesearch.php” caută un fișier XML pentru titluri care se potrivesc cu șirul de căutare (search string) și returnează rezultatul:
<?php
$xmlDoc=new DOMDocument();
$xmlDoc->load("links.xml");
$x=$xmlDoc->getElementsByTagName('link');
//obțineți parametrul q de la URL
$q=$_GET["q"];
//căutarea tuturor linkurilor din fișierul xml dacă lungimea lui q>0
if (strlen($q)>0) {
$hint="";
for($i=0; $i<($x->length); $i++) {
$y=$x->item($i)->getElementsByTagName('title');
$z=$x->item($i)->getElementsByTagName('url');
if ($y->item(0)->nodeType==1) {
//find a link matching the search text
if (stristr($y->item(0)->childNodes->item(0)->nodeValue,$q)) {
if ($hint=="") {
$hint="<a href='" .
$z->item(0)->childNodes->item(0)->nodeValue .
"' target='_blank'>" .
$y->item(0)->childNodes->item(0)->nodeValue . "</a>";
} else {
$hint=$hint . "<br /><a href='" .
$z->item(0)->childNodes->item(0)->nodeValue .
"' target='_blank'>" .
$y->item(0)->childNodes->item(0)->nodeValue . "</a>";
}
}
}
}
}
// Setați ieșirea la „nici o sugestie” dacă nu a fost găsit niciun indiciu
// sau la valorile corecte
if ($hint=="") {
$response="nici o sugestie";
} else {
$response=$hint;
}
//ieșire răspuns
echo $response;
?>
Dacă există un text trimis de la JavaScript (strlen($q)> 0), se întâmplă următoarele:
Încărcați un fișier XML într-un nou obiect XML DOM
Buclați-vă (Loop) prin toate elementele <title> pentru a găsi potriviri (matches) din textul trimis de JavaScript
Setează URL-ul și titlul corect în variabila „$response”. Dacă se găsesc mai multe potriviri (matches), toate potrivirile (matches) sunt adăugate la variabilă
Dacă nu se găsește nicio potrivire (matche), variabila „$response” este setată pe „fără sugestie”
AJAX Poll
PHP - Sondaj AJAX
Sondaj AJAX
Următorul exemplu va demonstra un sondaj în care rezultatul este afișat fără reîncărcare.
Exemplu explicat - Pagina HTML
Când un utilizator alege o opțiune, se execută o funcție numită "getVote()". Funcția este declanșată de evenimentul "onclick":
<html>
<head>
<script>
function getVote(int) {
if (window.XMLHttpRequest) {
// cod pentru IE7+, Firefox, Chrome, Opera, Safari
xmlhttp=new XMLHttpRequest();
} else { // cod pentru IE6, IE5
xmlhttp=new ActiveXObject("Microsoft.XMLHTTP");
}
xmlhttp.onreadystatechange=function() {
if (this.readyState==4 && this.status==200) {
document.getElementById("poll").innerHTML=this.responseText;
}
}
xmlhttp.open("GET","poll_vote.php?vote="+int,true);
xmlhttp.send();
}
</script>
</head>
<body>
<div id="poll">
<h3>Până acum vă plac PHP și AJAX?</h3>
<form>
Da:
<input type="radio" name="vote" value="0" onclick="getVote(this.value)">
<br>Nu:
<input type="radio" name="vote" value="1" onclick="getVote(this.value)">
</form>
</div>
</body>
</html>
Funcția getVote() face următoarele:
Creați un obiect XMLHttpRequest
Creați funcția care trebuie executată atunci când răspunsul serverului este gata
Trimiteți cererea dezactivată unui fișier de pe server
Observați că la URL se adaugă un parametru (vote) (cu valoarea opțiunii da sau nu)
Fișierul PHP
Pagina de pe server numită de JavaScript-ul precedent este un fișier PHP numit "poll_vote.php":
<?php
$vote = $_REQUEST['vote'];
//obțineți conținutul fișierului text (textfile)
$filename = "poll_result.txt";
$content = file($filename);
//puneți conținutul în tablou (array)
$array = explode("||", $content[0]);
$yes = $array[0];
$no = $array[1];
if ($vote == 0) {
$yes = $yes + 1;
}
if ($vote == 1) {
$no = $no + 1;
}
// introduceți voturi în fișierul txt (txt file)
$insertvote = $yes."||".$no;
$fp = fopen($filename,"w");
fputs($fp,$insertvote);
fclose($fp);
?>
<h2>Rezultat:</h2>
<table>
<tr>
<td>Da:</td>
<td>
<img src="poll.gif"
width='<?php echo(100*round($yes/($no+$yes),2)); ?>'
height='20'>
<?php echo(100*round($yes/($no+$yes),2)); ?>%
</td>
</tr>
<tr>
<td>Nu:</td>
<td>
<img src="poll.gif"
width='<?php echo(100*round($no/($no+$yes),2)); ?>'
height='20'>
<?php echo(100*round($no/($no+$yes),2)); ?>%
</td>
</tr>
</table>
Valoarea este trimisă de la JavaScript și se întâmplă următoarele:
Obțineți conținutul fișierului "poll_result.txt"
Puneți conținutul fișierului în variabile și adăugați unul la variabila selectată
Scrieți rezultatul în fișierul "poll_result.txt"
Prezentați o reprezentare grafică a rezultatului sondajului
Fișierul text
Fișierul text (poll_result.txt) este locul în care stocăm datele din sondaj.
Primul număr reprezintă voturile „Da”, al doilea număr reprezintă voturile „Nu”.
Nu uitați să permiteți serverului dvs. Web să editeze fișierul text. NU acorda acces tuturor, doar serverului web (PHP).
Oxizi
Structura, formula generală și nomenclatura oxizilor; oxizi acizi, oxizi bazici, oxizi amfoteri și oxizi indiferenți; proprietăți și metode generale de obținere a oxizilor.
Acizi
Definirea acizilor conform teoriei disociației electrolitice și a teoriei protolitice; hidracizi și oxoacizi; radicali acizi; formula generală și nomenclatura acizilor; proprietățile și reacțiile chimice specifice acizilor; ionizarea acizilor; metode generale de obținere a acizilor.
Baze
Definirea bazelor conform teoriei disociației electrolitice și teoriei protolitice; formula generală și nomenclatura bazelor; proprietățile și reacțiile chimice specifice bazelor; ionizarea bazelor; metode generale de obținere a bazelor.
Săruri
Structura și formula generală a sărurilor; săruri neutre, săruri acide și săruri bazice; nomenclatura sărurilor; proprietățile și reacțiile chimice ale sărurilor; metode generale de obținere a sărurilor; neutralizare și hidroliză.
Hidrogenul
Caracteristici generale ale hidrogenului; formarea ionului de hidrură, H-, și formarea ionului de hidrogen (proton), H+. Răspândirea hidrogenului în natură. Metode de preparare a hidrogenului. Proprietățile fizice și chimice ale hidrogenului. Hidruri. Ortohidrogen și parahidrogen. Hidrogenul atomic. Întrebuințările hidrogenului. Izotopii hidrogenului (protiu, deuteriu, tritiu).
Apa
Răspândirea apei în natură. Purificarea apei - sedimentare, filtrare, sterilizare. Apele industriale. Distiliarea apei. Apa higroscopică. Proprietățile fizice ale apei. Structura moleculei de apă. Proprietățile chimice ale apei. Hidrați.
Grupa 18 sau grupa a VIII-a principală
Grupa a VIII-a principală, numerotată VIII A sau 18, cuprinde gazele rare (nobile) heliu, He, neon, Ne, argon, Ar, kripton, Kr, xenon, Xe, radon, Rn.
Grupa 17 sau grupa a VII-a principală
Grupa a VII-a principală, numerotată VII A sau 17, numită și grupa halogenilor, conține următoarele elemente: fluor, F, clor, Cl, brom, Br, iod, I, astatin, At.
Grupa 16 sau grupa a VI-a principală
Grupa a VI-a principală a sistemului periodic, numerotată VI A sau 16, cuprinde elementele oxigen, O, sulf, S, seleniu, Se, telur, Te, și poloniu, Po.
Grupa 15 sau grupa a V-a principală
Grupa a V-a principală a sistemului periodic, numerotată V A sau 15, cuprinde următoarele elemente: azot, N, fosfor, P, arsen, As, stibiu (antimoniu), Sb, și bismut, Bi.
Grupa 14 sau grupa a IV-a principală
Grupa a IV-a principală a sistemului periodic, numerotată IV A sau 14, cuprinde elementele carbon, C, siliciu, Si, germaniu, Ge, staniu, Sn, și plumb, Pb.
Grupa 13 sau grupa a III-a principală
Grupa a III-a principală a sistemului periodic, numerotată III A sau 13, cuprinde elementele bor, B, aluminiu, Al, galiu, Ga, indiu, In, și taliu, Tl.
Grupa 2 sau grupa a II-a principală
Grupa a II-a principală a sistemului periodic, numerotată II A sau 2, cuprinde elementele: beriliu, Be, magneziu, Mg, calciu, Ca, stronțiu, Sr, bariu, și radiu, Ra. Această grupă se mai numește grupa metalelor alcalino-pământoase.
Grupa 1 sau grupa I principală
Elementele de tranziție
Structura electronică a elementelor de tranziție; caracteristicile chimice ale elementelor de tranziție.
Grupa 3 sau grupa a III-a secundară
Grupa a III-a secundară a sistemului periodic, numerotată III B sau 3, cuprinde elementele rare scandiu, Sc, ytriu, Y, și lantan, La, precum și elementul radioactiv actiniu, Ac.
Grupa 4 sau grupa a IV-a secundară
Grupa a IV-a secundară a sistemului periodic, numerotată IV B sau 4, cuprinde elementele rare titan, Ti, zirconiu, Zr, și hafniu, Hf.
Grupa 5 sau grupa a V-a secundară
Grupa a V-a secundară a sistemului periodic, numerotată V B sau 5, cuprinde elementele rare vanadiu, V, niobiu, Nb, și tantal, Ta.
Grupa 6 sau grupa a VI-a secundară
Grupa a VI-a secundară a tabelului periodic, numerotată VI B sau 6, cuprinde elementele crom, Cr, molibden, Mo, și wolfram, W.
Grupa 7 sau grupa a VII-a secundară
Grupa a VII-a secundară a sistemului periodic, numerotată VII B sau 7, cuprinde elementele mangan, Mn, technețiul, Tc, și reniu, Re.
Grupa 8 sau grupa a VIII-a secundară
Grupa 8 a sistemului periodic, în trecut considerată parte a grupei a VIII-a secundare, alături de grupele 9 și 10, cuprinde elementele fier, Fe, ruteniu, Ru, și osmiu, Os.
Grupa 9 sau grupa a VIII-a secundară
Grupa 9 a sistemului periodic, în trecut considerată parte a grupei a VIII-a secundare alături de grupele 8 și 10, cuprinde elementele cobalt, Co, rodiu, Rh, și iridiu, Ir.
Grupa 10 sau grupa a VIII-a secundară
Grupa 10 a sistemului periodic, în trecut considerată parte a grupei a VIII-a secundare, alături de grupele 8 și 9, cuprinde elementele nichel, Ni, paladiu, Pd, și platină, Pt.

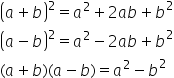
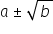 Expresii conjugate.
Expresii conjugate.