Legile Kirchhoff pentru reţele electrice.

Legile Kirchhoff

Prin circuit electric ramificat sau rețea electrică înțelegem un circuit care conține mai multe surse și mai mulți consumatori. Elementele unei rețele electrice sunt nodul, ramura și ochiul de rețea.

Nodul de rețea este orice punct de unde pornesc trei sau mai multe fire conductoare.

Ramura de rețea este orice porțiune continuă cuprinsă între două noduri pe care se află surse și consumatori. O ramură de rețea va fi parcursă de la un capăt la altul de același curent.

Ochiul de rețea este orice contur închis format din ramuri de rețea.

Legea I a lui Kirchhoff se referă la un nod de rețea și afirmă că suma algebrică a intensităților curenților într-un nod de rețea este nulă sau suma intensităților curenților care intră în nod este egală cu suma intensităților curenților care ies din nodul de rețea.

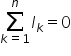
Legea a II-a se referă la ochiul de rețea și afirmă că pe un ochi de rețea suma algebrică a tensiunilor electromotoare aflate pe ramurile ochiului este egală cu suma algebrică a căderilor tensiune pe consumatorii aflați pe ramurile ochiului. Rezistențele interne ale surselor sunt luate ca și consumatori.

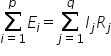
Pentru rezolvarea unei rețele electrice se parcurg următoarele etape:

1. Se identifică nodurile, ramurile și ochiurile de rețea notându-se nodurile cu litere mari.
2. Se aleg arbitrar sensuri ale curenților prin ramurile rețelei. Trebuie să avem atâția curenți câte ramuri.
3. Se aleg sensuri arbitrare de parcurs pentru fiecare ochi în parte.
4. Se scrie pentru fiecare nod legea I a lui Kirchhoff ținând cont de faptul că dacă curentul intră în nod atrunci el este pozitiv iar dacă iese din nod este negativ.
5. Se scrie pentru fiecare ochi de rețea legea a II-a a lui Kirchhoff astfel:
   • se parcurge ochiul în sensul ales pentru a obține suma algebrică a tensiunilor electromotoare, se iau ca pozitive tensiunile electromotoare ale surselor parcurse de la borna ”-” la borna ”+” și se iau ca negative tensiunile electromotoare ale surselor parcurse de la borna ”+” la borna ”-”;
   • se aprcurge ochiul în sensul ales pentru a obține suma algebrică a căderilor de tensiune pe ramurile ochiului de rețea, se iau ca pozitive căderile de tensiune U=IR pentru care sensul de parcurgere coincide cu sensul curentului prin ramură și se iau ca negative căderile de tensiune pentru care sensul de parcurgere este opus sensului curentului prin ramură;
   • la a doua parcurgere se ține cont și de căderile de tensiune date de rezistențele interne ale surselor.
6. Se alătură ecuațiile obținute din legea I și cele obținute din legea a II-a. Se obține un sistem format din atâtea ecuații câți curenți sau câte ramuri formează rețeaua.
7. Se rezolvă sistemul de ecuații obținându-se valorile intensităților curenților prin ramurile rețelei.