Triunghi oarecare
Tag-uri
Partajeaza in Google Classroom
Teorie: Triunghi oarecare Descarcă PDF
Triunghiul este o figură plană închisă, formată din trei laturi și trei vârfuri. Cele trei laturi ale unui triunghi sunt segmente, iar vârfurile sunt punctele de intersecție ale laturilor.
- punctele A, B, C se numesc vârfurile triunghiului.
- [AB], [BC], [AC] se numesc laturile triunghiului.
- ∠ B A C , ∠ A B C , ∠ A C B
se numesc unghiurile (interne) triunghiului.
Un triunghi care are laturile de lungimi diferite se numește triunghi oarecare (sau scalen).
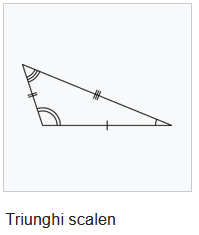
Proprietați:
Într-un triunghi oarecare, laturii mai mari i se opune un unghi mai mare decât cel care se opune laturii mai mici.
Într-un triunghi oarecare, măsura unui unghi exterior triunghiului este egală cu suma măsurilor unghiurilor interioare nealăturate. Un unghi exterior unui triunghi este mai mare decât oricare din unghiurile interne nealăturate.
Aria triunghiului oarecare
Formula lui Heron
În geometrie, formula lui Heron, este o expresie matematică prin care se poate calcula suprafața unui triunghi oarecare fiind date cele trei laturi.
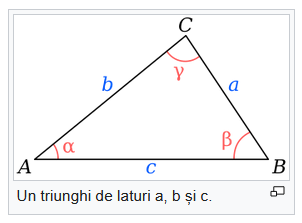
Dacă ABC este un triunghi oarecare, cu laturile a, b și c, atunci suprafața sa este dată de formula:


unde
Poate fi demonstrată trigonometric sau cu teorema lui Pitagora.
Alte forme ale formulei lui Heron:




![{\displaystyle [AB]\cup [BC]\cup [CA]=\triangle [ABC]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b4fc29b17a8101104eb534922becd82eb4e876)





