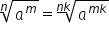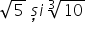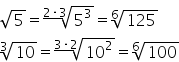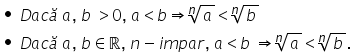Aducerea radicalilor la același ordin. Compararea radicalilor
Tag-uri
Partajeaza in Google Classroom
Transcript
în acest clip voi prezenta procedeul
prin care putem aduce radicalii
la același ordine astfel vom putea
să comparăm mai ușor doi radicali
și să efectuăm operații cu aceștia
pentru a compara doi radicali având
ordine diferite va trebui mai întâi
se aducem la același ordine iar
pentru aceasta vom folosi formula
aceasta prezentată în lecția trecută
radical de ordin n din a la m este
egal cu radical de ordin n k din
a la m k pentru a aduce radicali
la același ordin vom lua cel mai
mic multiplu comun al ordinelor
radicalilor primul radical este
de ordinul 2 Iar următorul radical
este de ordinul 3 în acest caz
cel mai mic multiplu comun al ordinelor
este 6 pentru a aduce primul radical
la ordinul 6 vom înmulțit ordinul
radicalului și exponentul numărului
de sub radical cu trei prin urmare
vom avea radical de ordin 2 ori
3 din 5 la a treia egal cu radical
de ordin 6 din 125 pentru a aduce
următorul radical la ordinul 6
vom înmulțirii ordinul radicalului
și exponentul numărului de sub
radical cu doi și vom avea radical
de ordin 3 ori 2 din 10 la a doua
egal cu radical de ordinul 6 din
100 Acum putem foarte ușor să comparăm
acești doi radical observăm că
100 este mai mic decât 125 prin
urmare radical de ordinul 6 din
100 va fi mai mic decât radical
de ordinul 6 din 125 în consecință
radical de ordinul 3 din 10 este
mai mic decât radical din 5 următorul
exercițiu Să se compare numerele
radical de ordinul 6 din 25 și
radical de ordinul 4 din 5 la a
treia va trebui mai întâi să aducem
radicali la același ordin mai întâi
vom Rescrie radical de ordinul
6 din 25 astfel radical de ordinul
6 din 5 la a doua cel mai mic multiplu
comun al numerelor 6 și 4 este
12 iar să aducem radicali la ordinul
12 pentru aceasta vom înmulțit
ordinul radicalului și exponentul
numărului de sub radical cu doi
și vom avea radical de ordinul
șase ori 2 din 5 la 2 ori 2 egal
cu radical de ordinul 12 din 5
la a patra deocamdată lăsăm așa
urmează apoi radical de ordinul
4 din 5 la a treia ca să aducem
acestei radical la ordinul 12:00
trebuie să înmulțim ordinul radicalului
și exponentul puterii cu trei și
vom avea radical de ordinul 4 ori
3 din 5 la puterea 3 ori 3 egal
cu radical de ordinul 12 din 5
la a noua ne uităm acum la numerele
de sub radical observăm că cinci
la a patra este mai mic decât 5
la a noua prin urmare radical de
ordinul 12 din 5 la a patra va
fi mai mic decât radical de ordinul
12 din 5 la noua Așadar radical
de ordinul 6 din 25 este mai mic
decât radical de ordinul 4 din
5 la a treia un ultim exercițiu
tăcere să ordonând crescător numerele
radical din 2 radical de ordin
3 din 4 și radical de ordinul 4
din 5 primul radical este de ordinul
2 iar cel mai mic multiplu comun
al numerelor 2 3 și 4 este 12 Așadar
ordinul radicalilor va fi 12 ca
să aducem radical din 2 la un radical
de ordin 12 va trebui să înmulțim
ordinul radicalului și exponentul
puterii cu șase Așadar vom avea
radical de ordinul 2 ori 6 din
2 la 6 egal cu radical de ordinul
12 din 2 la a 6-a Care este 64
radical de ordinul 3 din 4 va fi
radical de ordinul 3 ori 4 din
4 la a patra am înmulțit cu 4 atât
ordinul radicalului cât și exponentul
numărului de sub radical și obținem
radical de ordinul 12 din 4 la
a patra 4 la a patra este 16 la
a doua adică 256 radical de ordinul
4 din 5 va fi egal cu radical de
ordinul 4 ori 3 din 5 la a treia
egal cu radical de ordinul 12 din
125 ne uităm acum la numerele de
sub radical 64 este mai mic decât
125 și mai mic decât 256 prin urmare
radical de ordin 12 din 64 e mai
mic decât radical de ordin 12 din
125 Care este mai mic decât radical
de ordin 12 din 256 În consecință
tradi cal din 2 este mai mic decât
radical de ordinul 4 din 5 Care
este mai mic decât radical de ordinul
3 din 4
Compararea radicalilorAscunde teorie X
Navigare în lectii
Cumpara abonament
