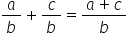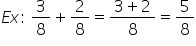Adunarea fracţiilor ordinare
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să învățăm
să adunăm fracțiile ordinare cu
același numitor sau cu numitorii
diferiți Și începem cu adunarea
fracțiilor având același numitor
un prim exemplu 3 supra 4 plus
7 supra 4 atunci când trebuie să
adunăm două fracții care au același
numitor se adună numărătorii iar
numitorul se copiază obținem 3
plus 7 supra 4 egal 10 supra 4
această fracție se mai poate simplifica
cu 2 și obținem 5 supra 2 al doilea
exemplu 5 supra 6 plus 11 supra
6 adunăm numărătorii 5 plus 11
totul supra 6 egal cu 16 supra
6 putem să simplificăm cu 2 și
obținem 8 supra 3 rețineți Așadar
că atunci când adunăm două fracții
cu același numitor se adună numărător
iar numitorul se copiază să vedem
cum putem să adunăm fracțiile care
au numitorul diferiți Uneori în
exercițiile mai simple când avem
la numitori numere mai mici putem
deduce imediat numitorul comun
însă alte ori este mai dificil
de observat numitorul comun și
atunci trebuie să urmăm Niște etape
mai întâi aflăm cel mai mic multiplu
comun al numitorilor acesta va
fi numitorul comun și apoi împărțind
numitorul comun la numitorul fiecărei
fracții și amplificăm fracția respectivă
cu câtul obținut o să înțelegeți
mai bine după ce facem câteva exemple
un prim exemplu 3 supra 5 plus
doi supra 10 cel mai mic multiplu
comun al numerelor 5 și 10 va fi
10 deoarece 10 este un multiplu
al lui 5 în acest caz trebuie să
amplificăm prima fracție cu doi
pentru a obține la numitor 10 deoarece
2 ori 5 este 10-a da Va rămâne
așa și obținem 2 ori 3 6 supra
10 plus 2 supra 10 egal în continuare
cu 6 plus 2 supra 10 egal cu 8
supra 10 putem să simplificăm cu
2 și obținem 4 supra 5 b 1 supra
3 plus 3 supra 4 având în vedere
că numerele 3 și 4 sunt numere
prime între ele cel mai mic multiplu
comun al acestora va fi produsul
lor adică trei ori 412 ca să obținem
12 la numitorul primei fracții
trebuie să o amplificăm cu 4 iar
a doua fracție trebuie amplificată
cu 3 4 ori 1 este 4 iar 43 12 plus
3 ori 3 este 9 și 3 ori 4 12 acum
adunăm numărătorii 4 plus 9 iar
numitorul comun se copiază și obținem
egal cu 13 supra 12 un întreg 3
supra 7 plus 2 întregi 1 supra
3 pentru a introduce întregii în
fracție îmi face unu ori șapte
plus trei totul supra 7 numitorul
se copiază Plus 2 ori 3 plus 1
totul supra 3 egal 7 plus 3 y este
10 supra 7 plus 2 ori 3 este 6
plus 1 7 supra 3 având în vedere
că avem două fracții cu numitori
diferiți pentru a le aduna trebuie
să le aducem la numitor comun numitorul
comun va fi 7 ori 3 adică 21 amplificăm
prima fracție cu trei și a doua
fracție cu 7 3 ori 10 este 30 supra
21 plus 77 este 49 supra 21 egal
30 și cu 49 este 79 supra 21 urmează
punctul d 1 supra 4 plus 3 supra
8 plus 5 supra 12 descompunem numitorii
4 este 2 la puterea a doua 8 este
2 la puterea a treia pentru cei
care nu pot să le descompună direct
facem alăturat 8 împărțit la 2
este 4 4 împărțit la 2 este 2 2
împărțit la 2 este cu 1 ciudați
compunem acum pe 12 12 împărțit
la 2 este 6 6 împărțit la 2 este
3 3 împărțit la 3 este 112 va fi
egal cu 2 la puterea a doua ori
3 acum aflăm cel mai mic multiplu
comun al numerelor 4 8 și 12 acesta
va fi egal cu 2 la puterea a treia
ori 3 2 la a treia este 8 ori 3
adică 24 Deci numitorul comun este
24 și acum împărțim acest numitor
la numitorul fiecărei fracții 24
împărțit la 4 este 6 ești prima
fracție se va amplifica cu șase
24 împărțit la 8 va fi 3 amplificăm
a doua fracție cu 3 și 24 împărțit
la 12 este egal cu doi amplificăm
3-a fracție cu 2 și obținem 6 supra
24 plus 9 supra 24 plus 10 supra
24 egal 6 plus 9 este 15 plus 10
este 25 supra 24 urmează punctul
E 1 supra 8 plus 7 supra 10 plus
4 supra 25 descompunem numitorii
în factori primi opt este egal
cu doi la puterea a treia 10 este
egal cu 2 ori 5 iar 25 este egal
cu 5 la puterea a doua acum aflăm
cel mai mic multiplu comun al numerelor
8 10 și 25 acesta este egal cu
2 la puterea a treia ori 5 la puterea
a doua egal cu opt ori 25 și egal
cu 200 Deci numitorul comun este
200 acum împărțim numitorul comun
la numitorul fiecărei fracții 200
împărțit la 8 este 25 pentru că
am văzut cu opt ori 25 de de 200
de ce amplifică în prima fracție
cu 25 200 împărțit la 10 este 20
iar 200 împărțit la 25 este opt
ultima fracție trebuie amplificată
cu opt egal cu 25 supra 200 Plus
20 ori 7 este 140 supra 200 plus
8 ori 4 este 32 supra 200 penal
25 plus 140 este egal cu 165 supra
200 putem să adunăm primele două
fracții deoarece adunarea este
asociativă Plus 32 supra 200 iar
165 Plus 32 este egal cu 197 supra
200 Aceasta este o fracție ireductibilă
Deci rezultatul rămâne sub această
formă și ultimul exercițiu punctul
f 9 supra 20 plus 4 supra 15 plus
7 supra 9 plus 53 supra 180 descompune
mai întâi pe 2020 se împart la
2 și obțin m10 10 împărțit la 2
este 5 5 împărțit la 5 este 120
de L cu 2 la a doua ori 515 se
împarte la 3 și obținem 5 5 împărțit
la 5 este 1 15 egal cu 3 ori 5
nu am este 3 la a doua 180 având
în vedere că ultima sa cifră este
0 acest număr va fi divizibil cu
10 adică împărțim la doi ori cinci
cine rămâne 1818 se împarte la
2 și este 9 9 împărțit la trei
este trei trei împărțit la trei
este una 180 este egal cu 2 la
a doua ori 3 la a doua ori cinci
cel mai mic multiplu comun al numerelor
2015 nouă și 180 este 2 la a doua
ori 3 la a doua ori 5 adică 180
180 împărțit la 20 este 9 Deci
prima fracție trebuie amplificată
cu 9 acum facem 180 împărțit la
numitorul celei de a doua fracții
adică la 15 Nerf 12 amplificăm
a doua fracție cu 12 180 împărțit
la 9 este 20 amplifică a treia
fracție cu 20 și ultima fracție
Rămâne așa deoarece aceasta are
deja numitorul 180 nu ori nu este
81 supra 180 plus 12 ori 4 este
48 supra 180 plus 20 ori 7 este
140 supra 180 plus 53 supra 180
egal 81 și cu 48 este 129 supra
180 plus putem adună primele două
fracții și ultimele două fracții
deoarece adunarea este asociativă
140 și cu 53 este 193 supra 180
9 și cu 312 1 reținem 9 și cu 211
cu 112 1 și cu unu doi și cu unu
de trei 322 supra 180 simplificăm
cu 2 și obținem 161 supra 90