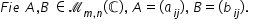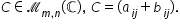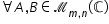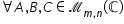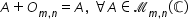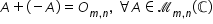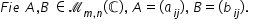Adunarea matricelor

deoarece elementele unei Matrice

sunt numere operațiile cu Matrice

sunt generate de operațiile pe

care le putem face cu numere putem

vorbi așa dar de adunarea matricelor

Să considerăm două Matrice matricea

a de tipul 2 3 cu elemente numere

întregi și matricea b tot de tipul

2 3 cu elemente numere întregi

putem să ne imaginăm că cele două

Matrice reprezintă stocurile de

materiale înregistrate în luna

ianuarie matricea a pentru produsele

pe 1 pe 2 în depozitele de 1 de

2 respectiv de 3 în același timp

matricea b reprezintă stocurile

de materiale din luna februarie

pentru aceleași produse pe 1 și

pe 2 în același depozite de unul

de doi și de trei de dorința știm

ce cantități Din produsul pe 1

avem pe stoc În depozitul de 1

la finalul celor două luni Evident

vom aduna numărul unu cu numărul

2 adică elementul de pe linia 1

coloana 1 din matricea a respectiv

elementul din linia 1 respectiv

coloana 1 din matricea b vom proceda

în același mod și cu celelalte

elemente efectuând calculele obținem

o matrice de tipul 2 3 cu elemente

din z elemente care sunt trei trei

șase șapte zero șase Matrice care

se numește suma matricelor a și

b și o notăm a plus b iar operația

prin care am obținut această Matrice

o numim adunarea matricelor Am

observat că suma a două Matrice

se obține din adunarea elementelor

aflate pe aceleași poziții în cele

două Matrice motiv pentru care

nu putem adunat decât Matrice de

același tip noțiunea de opusă a

unui număr de sugerează noțiunea

de opusă a unei Matrice dată matricea

a de tipul 2 3 opusă acesteia este

matricea notată minus se tot de

tipul 2 3 în care elementele sunt

opuse al elementelor matricei a

minus 1 minus 2 minus 3 minus 4

0 și minus 1 pentru că adunarea

matricelor înseamnă adunarea elementelor

corespunzătoare proprietățile aceste

operații se Rezumă la proprietățile

adunării numerelor complexe astfel

adunarea matricelor este asociativă

este comutativă admitere element

neutru matricea nulă de tipul m

n pentru orice Matrice de tipul

Yemen există o matrice notată minus

a și numită Matrice opusă de tipul

MN astfel încât a adunată cu opusă

a ne dă matricea nulă de tipul

MN pentru a efectua scăderea Să

considerăm matricea a de tipul

3 2 și matricea b de tipul 3 2

matricea a minus b reprezintă suma

dintre matricea a și opus a matricei

b adică matricea unu cinci doi

minus unu trei doi adunată cu matricea

minus trei unu minus patru minus

doi cinci trei obținând astfel

matricea 1 minus 3 5 plus 1 2 minus

4 minus 1 minus 2 3 plus 5 2 plus

3 adică matricea a minus 2 6 minus

2 minus 3 8 5 să rezolvăm acum

următorul exercițiu date trei Matrice

a b și c Determinați numerele reale

x y z astfel încât matricea a plus

matricea b să fie egală cu matricea

ce conform definiției adunării

o matrice suma matricelor a și

b se obține adunând elementele

corespunzătoare din matricea a

respectiv matricea b astfel elementul

a11 adunat cu elementul b 1 1 este

egal cu elementul C11 elementul

a11 este 1 elementul b11 este radical

din x plus 1 care este egal cu

elementul 1 deducem de aici că

radical din x plus 1 egal cu zero

adică XS egal cu minus unu adunând

acum elementul a21 cu elementul

de 2 1 obținem elementul c21 adică

numărul 2 adunat cu 2 la puterea

a t este egal cu 4 2 la 3 este

egal cu 4 minus 2 adică 2 cu funcția

exponențială este o funcție injectivă

obținem Așadar că te este egal

cu 1 elementul a12 adunat cu elementul

B12 este egal cu elementul C12

adică 3 plus logaritm natural din

z este egal cu 2 logaritm natural

din 0 este astral egal cu 2 minus

3 adică minus unu îl putem scrie

pe minus unu ca logaritm natural

din e la puterea minus 1 în baza

injectivitatii funcției logaritmice

îl de ducem pe Zet ca fiind egal

cu i la puterea minus 1 pentru

al determina pe Y8 Suma a doi doi

adunat cu d22 care este egal cu

c22 pe elementul a22 este egal

cu 5 elementul B 2.2 este la a

doua minus 3x la obținem ecuația

de gradul al doilea la a doua minus

3x 2 egal cu 0 care are soluțiile

1 este egal cu 1 respectiv y 2

egal cu 2