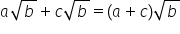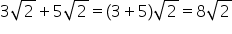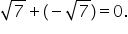Adunarea numerelor reale
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție o să învățăm
să adunăm numerele reale adunarea
a două numere reale a și b este
un număr real si notat cu a plus
b care se numește suma numerelor
a și b Adunarea numerelor reale
are următoarele proprietăți asociativitatea
acest lucru înseamnă că între o
sumă putem să asociem termenii
diferit iar rezultatul rămâne neschimbat
comutativitatea putem să inversăm
locul termenilor iar rezultatul
Rămâne același 0 este element neutru
pentru adunare Orice număr real
a adunat cu zero va fi acel număr
a și orice număr real X are un
opus notat cu minus x astfel încât
x adunat cu minus x să fie 0 nu
faci un exemplu în care o să evidențiem
aceste proprietăți ale adunării
numerelor reale calcula radical
din 3 plus 5 plus minus radical
din 3 în prima paranteză o să inversez
locul termenilor vei scrie cinci
plus radical din trei plus minus
radical din 3 adunarea este și
asociativă deci putem să asociem
ultimii doi termeni egal cu 5 plus
paranteză dreaptă radical din trei
plus minus radical din 3 egal radical
din trei și minus radical din 3
sunt numere reale opuse de județul
tratul la adunărilor va fi 0 obținem
Așadar 5 plus zero zero este neutru
de rezultatul final va fi 5 după
proprietățile adunării numerelor
reale sunt aceleași ca și la Adunarea
numerelor raționale trebuie sa
vedem cum putem aduna numerele
iraționale pentru a aduna mai multe
numere reale de formă a radical
din b care au același număr sub
radical se adună factorii din fața
radicalilor iar rezultatul se înmulțește
cu radicalul de exemplu 3 radical
din 5 plus 4 radical din 5 va fi
egal cu 3 plus 4 înmulțit cu radical
din 5 atenție numerele de sub radical
nu se adună egal mai departe cu
7 radical din 5 nu face câteva
adunări primul exercițiu minus
4 plus 6 plus radical din 2 minus
4 plus 6 este 2 plus radical din
2 având în vedere că radical din
2 este un număr irațional Acesta
are o infinitate de zecimale de
obicei Se preferă ca numerele iraționale
să fie lăsate sub formă de radical
doar în cazul în care dorim totuși
un rezultat aproximativ numai aproximat
numărul radical din 2 cu 1 și 1
Deci obținem în continuare un rezultat
aproximativ egal cu 2 plus 1 care
va fi egal cu 3 dar după cum spuneam
numerele iraționale se vor lăsa
sub formă de radical al doilea
exercițiu radical din 5 plus radical
din 5 coeficientul acestor radical
este 1 pentru a aduna cei doi radical
se adună cu eficienți lor scrie
1 plus 1 iar numărul irațional
se copiază egal cu 2 radical din
5 nu se mai scrie semnul ori între
2 și radical din 5 ma de exemplu
2 radical din 3 plus 5 radical
din 3 și în acest caz o să adunăm
coeficienții doi plus cinci totul
ori radical din 3 egal cu 7 radical
din 3 4 minus 3 radical din 2 plus
2 radical din 2 plus 7 radical
din 2 va fi egal cu minus 3 plus
2 plus 7 totul înmulțit cu radical
din 2 minus trei plus doi este
minus 1 plus 7 este 6 radical din
2 5 minus 5 radical din 7 plus
3 radical din 7 plus 2 radical
din 7 egal cu minus 5 plus 3 plus
2 radical din 7 minus 5 plus 3
este minus 2 iar minus 2 plus 2
este 0 obținem 0 radical din 7
Care este zero pentru că zero înmulțit
cu orice numar este 0 6 nu radical
din 11 plus 5 radical din 11 plus
minus 9 radical din 11 observăm
că în această sumă Avem două numere
reale opuse 9 radical din 11 și
minus 9 radical din 11 atunci când
adunăm două numere reale opuse
Rezultatul este 0 deci noi putem
să anticipăm că adunând 9 radical
din 11 cu minus 9 radical din 11
vom obține 0 și atunci putem să
reducem acești termeni îi vom tăia
cu o linie oblică din această sumă
mai rămâne doar 5 radical din 11
7 13 radical din 5 plus radical
din 5 plus minus 2 radical din
5 din el putem să ne obișnuim să
facem acestei adunări ale coeficienților
în minte fără să mai scriem în
paranteză suma acestora 13 adunat
cu unu este 14 minus doi este egal
cu 12 radical din 5 și ultimul
exercițiu 2 radical din 10 plus
4 radical din 5 plus 3 radical
din 10 plus 5 radical din 5 Ați
observat că până acum am avut doar
exerciții în care apăreau radicali
asemenea adică sub radical am avut
același număr în acest exercițiu
apară radical diferiți avem și
radical din 10 și radical din cinci
în cel de sumă se vor aduna doar
radicali asemenea termenii asemenea
Bull știi 2 radical din 10 și 3
radical din 10 iar ceilalți termeni
asemenea sunt 4 radical din 5 și
5 radical din 5 2 radical din 10
plus 3 radical din 10 este egal
cu 5 radical din 10 iar 4 radical
din 5 plus 5 radical din 5 este
egal cu 9 radical din 5 rezultatul
va rămâne sub această formă de
oarece nu putem să adunăm doi radicali
diferiți

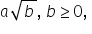 care au același număr sub radical, se adună factorii din fața radicalilor, iar rezultatul se înmulțește cu radicalul.
care au același număr sub radical, se adună factorii din fața radicalilor, iar rezultatul se înmulțește cu radicalul.