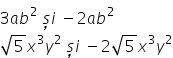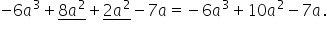Adunarea și scaderea numerelor reale reprezentate prin litere

adunarea și scăderea numerelor

reale reprezentate prin litere

în operațiile cu numere reale pe

care le vom efectua în continuare

prin litere desemnăm numere reale

oarecare o succesiune de adunări

de numere reale se numește sumă

algebrică termenii unei sume algebrice

pot fi numere reale sau produse

dintre un număr real și numere

reale reprezentate prin litere

doi termeni în care apar aceleași

litere cu același exponent se numesc

termenii asemenea de exemplu 3a

b la a doua și minus 2-a b la a

doua vor fi termeni asemenea doi

termeni asemenea au aceeași parte

literală a b la a doua a b la a

doua numărul care însoțește partea

literală se numește coeficientul

termenului în primul caz coeficientul

este 3 iar în al doilea caz coeficientul

este minus 2 un alt exemplu minus

radical din 3x la a treia și 2

radical din 3 x la a treia și aceștia

vor fi termeni asemenea coeficientul

primului termen este minus radical

din trei iar coeficientul celui

de al doilea termen este 2 radical

din 3 pentru suma algebrică putem

aduna doar termeni asemenea mai

exact se adună coeficienților iar

partea literală se copiază primul

exercițiu 5x plus 2x Aceștia sunt

termeni asemenea și adunăm coeficienților

5 plus 2 este 7 iar partea literală

se copiază ținem 7 x 2 2a la a

doua minus 6-a la a doua 2 minus

6 este minus 4 a la a doua 3 7

x plus 2y minus 40 minus 5x plus

6 y plus 3 z termenii asemenea

sunt 7x și minus 5X apoi 2y cu

plus 6 y și minus 40 cu 30 7 x

minus 5x este 2x 2y plus 6 y este

8 y și minus 40 plus 30 este minus

10 exercițiul numărul 4 x la a

treia minus 6x la a doua plus 3x

minus paranteză x la a treia plus

4x la a doua minus 5X mai întâi

desfacem paranteza ținând cont

de faptul că semnul minus în fața

unei paranteze a va schimba semnele

termenilor din paranteză până la

paranteză copiem x la a treia minus

6 x la a doua plus 3x minus x la

a treia minus 4x la a doua plus

5x egal termenii asemenea sunt

x la a treia și minus x la a treia

având semne opuse și același coeficient

a se vor reduce Deci o să îi tăiem

cu o linie oblică apoi minus 6

x la a doua minus 4x la a doua

este minus 10 x la a doua și mai

avem termeni asemenea trei x plus

cinci x care este egal cu 8 x următorul

exercițiu 5 radical din doi la

treia plus radical din doi la treia

minus 5 radical din 2 la a treia

pod acești termeni sunt termenii

asemenea și atunci trebuie să adunăm

coeficienții lor o să scriem între

paranteze cu eficienți lor pentru

a nu greșim radical din 2 plus

radical din 2 minus 5 radical din

2 totul înmulțit cu Ela treia radical

din 2 plus radical din 2 este 2

radical din 2 minus 5 radical din

2 obținem minus 3 radical din 2

L la a treia 6 2x plus 6 minus

paranteză 2x plus 8 desfacem parantezele

2 x plus 6 minus 2x minus 8 Ce

reduceri 2x și minus 2x pentru

că sunt numere reale opuse și rămâne

6 minus 8 Care este minus 2 7 3

pe lângă x la a doua plus 4x minus

4 închidem paranteza minus paranteză

3x pătrat plus 10 x minus 11 egal

ca să desfacem prima paranteză

folosind distributivitatea înmulțirii

față de adunare și scădere adică

nu țin numărul 3 cu fiecare număr

din paranteză și obținem 3x la

a doua plus 12 x minus 12 și aici

schimbăm semnele tuturor termenilor

din paranteză minus 3 x pătrat

minus 10 x plus 11 egal 3x pătrat

minus 3x pătrat este 0 12 x minus

10 x este 2 x și minus 12 plus

11 este minus 1 următorul exercițiu

8 minus 2 la a doua B plus 6-a

b la a doua plus 5-a la a doua

B minus 3 a b la a doua termenii

asemenea sunt minus doi a la a

doua B cu 5-a la a doua B și 6-a

b la a doua cu minus 3-a b la a

doua minus 2 plus 5 este 3-a la

a doua B și șase minus trei este

plus trei a b la a doua și ultimul

exercițiu radical din 2 x plus

radical din 3 y egal din 8x minus

radical din 27 y egal desfacem

paranteza până la paranteză copiem

radical din 2x plus radical din

3 y 1 radical din 8 x plus radical

din 27 y vom descompune 8 și 27

pentru a putea a scoate factorii

de sub radical 8 se împarte la

doi și este patru patru părți la

doi doi doi împărțit la doi unu

Deci radical din 8 este 2 radical

din 2 descompuneri și numărul 27

27 împărțit la 3 9 împărțit la

trei trei împărțit la trei unu

radical din 27 este egal cu 3 radical

din 3 egal cu radical din 2x plus

radical din 3 y 1 loc de radical

din 8 voi scrie 2 radical din 2

x plus în loc de radical din 27

100 scriem 3 radical din 3 y egal

termenii asemenea sunt radical

din 2x cu minus 2 radical din 2

x și radical din 3 y cu 3 radical

din 3 y radical din 2 minus 2 radical

din 2 este minus radical din 2

x și radical din 3 plus 3 radical

din 3 este 4 radical din 3 y