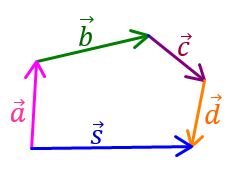
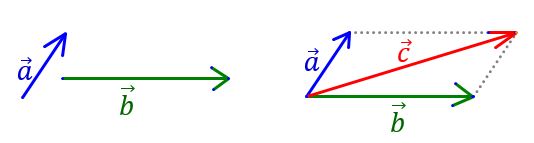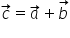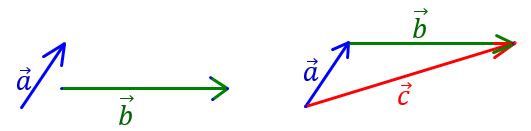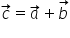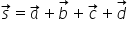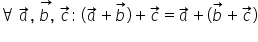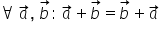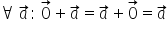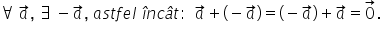Adunarea vectorilor (aplicații)

salut în lecția aceasta o să facem

câteva aplicații Iată avem aceste

puncte m n p q r și cele patru

cerințe la punctul a se cere să

calculăm suma vectorilor m p plus

p plus r m Iată vectorul m p p

r și r m pentru a aduna acești

trei vectori Folosind regula Poligonului

rezultanta sau vectorul sumă se

obține unind origine a primului

Vector cu extremitatea ultimului

Vector în să observăm că cele două

puncte coincid pentru că originea

a prim unui Vector este punctul

m iar extremitatea ultimului Vector

este de asemenea punctul M Așadar

rezultatul acestei sume este vectorul

nul dar Haideți să și arătăm acest

lucru mp plus pe r plus r m Știind

că adunarea vectorilor este asociativă

prin urmare putem să adunăm primii

doi vectori m p plus p r Folosind

regula triunghiului iar rezultatul

acestei sume tuffy vectorul m r

la care este adună vectorul r m

în să observăm că acești doi vectori

sunt opuși pentru că ei au aceeași

direcție același modul dar sensuri

contrare prin urmare vectorul r

m este opusul vectorului m r avem

m a r plus minus m r așa se notează

opusul vectorului m r iar suma

a doi vectori opuși este vectorul

nul am terminat cu punctul A continuăm

cu punctul b trebuie să adunăm

vectorul m p yatour plus pq plus

Q N plus and Air observăm că putem

să aplicăm regula Poligonului deoarece

fiecare Vector începând cu al doilea

are originea în extremitatea vectorului

anterior prin urmare aplicăm regula

Poligonului iar rezultanta sau

vectorul sumă va fi m r rezultatul

se obține unind originea primului

Vector adică punctul M cu extremitatea

ultimului Vector adică punctul

R vectorul obținut va fi m r trecem

la punctul c avem mp plus q m Știind

că adunarea vectorilor este comutativă

prin urmare putem să inversăm ordinea

acestor vectori și vom scrie q

m plus m p a făcut acest lucru

pentru a putea aplica regula triunghiului

avem Așadar vectorii q m și m p

vectorul sumă se obține un unde

punctul q cu punctul P mai exact

originea vectorului sumă va fi

în punctul q iar extremitatea în

punctul P iar rezultatul este vectorul

cupe și punctul de avem mp plus

un Plus pq plus n m folosim și

aici comutativitatea și asociativitatea

adunării și grupăm vectori astfel

Mai întâi m p plus p q plus un

plus n m mp plus pq va avea ca

rezultat vectorul mq iar t a folosi

regula triunghiului iar Q N plus

and m va avea ca rezultat vectorul

qm observăm că acești doi vectori

m q și q m sunt vectori opuși aceștia

au aceeași direcție și același

model dar sensuri contrare prin

urmare vectorul m este opusul vectorului

m q m q plus minus m q iar suma

a doi vectori opuși este vectorul

nul și mai facem încă un exercițiu

Fie a b c d un dreptunghi am notat

cu o intersecția diagonalelor iar

punctul m este mijlocul laturii

ab la punctul a se cere să calculăm

suma vectorilor de ce iartă și

b o ca să putem aduna cinci și

doi vectori după regula triunghiului

De exemplu a trebuit ca originea

celui de al doilea Vector să coincidă

cu extremitatea a primului Vector

dar observăm că vectorul bc este

egal cu vectorul AB cei doi vectori

au același modul aceeași direcție

și același sens prin urmare în

locul vectorului de ce putem să

scriem ab plus b o Acum putem să

aplicăm aici regula triunghiului

iar rezultatul va fi vectorul AO

Iată vectorul sumă va avea originea

în origine a primului Vector adică

punctul A și extremitatea în extremitatea

celui de al doilea Vector adică

punctul of trecem la punctul B

trebuie să adunăm vectorul ad Cum

vectorul ab și cu vectorul ce a

putem să adunăm vectorii ad și

ab Folosind regula paralelogramului

dreptunghiul este tot un paralelogram

Așadar suma acestor doi vectori

va fi diagonala paralelogramului

AC Prin urmare avem ace plus si

ei însă vectorul AC yatour este

opusul vectorului ce a aceștia

au aceeași direcție același modul

dar sensuri contrare Așadar avem

minus c a plus c a adunând doi

vectori opuși obținem vectorul

nul continuăm cu punctul c avem

o a plus b o plus de ce vă las

să vă gândiți până scriu eu mai

întâi folosim comutativitatea adunării

și inversăm acești doi vectori

vom scrie egal cu b o plus o a

apoi observăm că vectorul de ce

este egal cu vectorul AB Iată Așadar

vom scrie în continuare plus ab

pentru că acești doi vectori de

c și a b sunt vectori egali acum

adunăm vectorii b o și o am folosim

regula triunghiului b o plus o

a este egal cu vectorul Ba ia atât

și avem o b a plus a b a și a b

sunt vectori opuși vom scrie b

a plus minus b a c egal cu vectorul

nul și continuăm cu punctul d avem

de a plus c d plus MD plus MC puteți

să vă gândiți până scriu eu nu

folosi comutativitatea și asociativitatea

adunării și adunăm mai întâi acești

doi vectori de a plus MD apoi si

b plus m c în paranteze inversăm

ordinea vectorilor și avem m d

plus da plus m c plus c b dar MD

plus d a este egal cu m a iar m

c plus c b este egal cu MB să nu

uităm că punctul m este mijlocul

segmentului AB Așadar vectorii

m a și m b au același modul aceeași

direcție și sensuri contrare Așadar

aceștia vor fi vectorii opuși în

consecință avem m a plus minus

ma iar suma de electori opuse este

vectorul nul e bine să rețineți

această observație dacă avem un

segment AB iar m este mijlocul

segmentului atunci acești doi vectori

m a și m b sunt vectori opuși iar

rezultatul adunării lor va fi intotdeauna

a vectorul nul