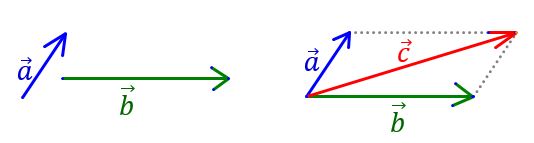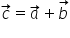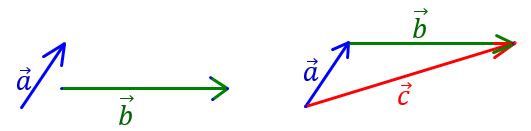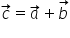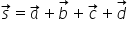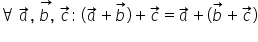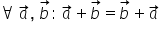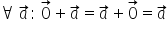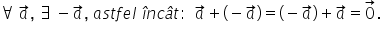Adunarea vectorilor (teorie)

în această lecție o să discutăm

despre adunarea vectorilor O primă

metodă prin care putem să adunăm

vectorii a și b este metoda paralelogramului

pentru aceasta vom translatat cei

doi vectori astfel încât aceștia

să aibă aceeași origine apoi prin

extremitatea vectorului a vom construi

o paralelă la Direcția vectorului

b iar prin extremitatea vectorului

B construim o paralelă la Direcția

vectorului a observăm că sa format

astfel un paralelogram având alaturi

cei doi vectori a și b iar diagonala

paralelogramului va fi suma celor

doi vectori a și b Iată acest Vector

este vectorul suma a plus b să

vedem și un alt exemplu Iată avem

acești doi vectori uși v o să îi

translator astfel încât cei doi

vectori să aibă aceeași origine

observăm că unghiul făcut de direcțiile

acestor doi vectori este un unghi

obtuz procedăm ca și mai sus aplicăm

regula paralelogramului iar pentru

aceasta vom construi prin extremitatea

vectorului u o paralelă la Direcția

vectorului V iar prin extremitatea

a vectorului v o paralelă la Direcția

vectorului 1 se formează astfel

un paralelogram iar diagonala acestui

paralelogram va fi suma lecturilor

u și v această regula paralelogramului

se poate aplica doar atunci când

avem doi vectori în cazul în care

avem mai mulți vectorii vom folosi

regula triunghiului o să vedem

această regulă pornind tot de la

doi vectori pentru a aplica metoda

triunghiului 100 translată vectorul

b astfel încât originea acestuia

să coincidă cu extremitatea vectorului

a Iată și acum unind originea vectorului

a cu extremitatea vectorului b

se obține vectorul sumă acesta

este vectorul suma a plus b în

cazul în care avem mai mulți decât

ori vom folosi această regulă a

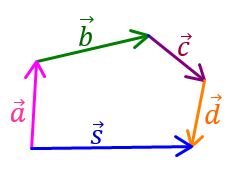
triunghiului extinsă de fapt ia

se va numi regula Poligonului Iată

avem patru vectori mai întâi vom

așeza vectorii b c și d astfel

încât originea acestora să coincidă

cu extremitatea a vectorului precedent

Iată și acum unind originea vectorului

a cu extremitatea vectorului de

se obține vectorul suma acest Vector

va fi suma vectorilor a b c și

d această regulă folosită se numește

regula Poligonului să vedem în

continuare care sunt proprietățile

operației de adunare a vectorilor

adunarea vectorilor este asociativă

oricare ar fi trei vectori a b

și c are loc această relație a

plus b adunat cu c este egal cu

a plus b plus c deci putem să grupăm

vectorii cum dorim iar rezultatul

sumei rămâne neschimbat adunarea

vectorilor este comutativă vectorul

a plus vectorul b este egal cu

vectorul b plus vectorul a există

element neutru vectorul nul vectorul

nul adunat cu vectorul a este egal

cu vectorul a și ultima proprietate

a adunării existența elementului

opus asta înseamnă că fiecare Vector

a are un opus notat cu minus a

astăzi În cât a adunat cu opusul

său să dea vectorul nul o să vizualizam

acestei proprietăți Pe un desen

avem în această figură trei vectori

a b și c vectorul a este cel mai

dens yacht cu roz vectorul b este

cu galben și vectorul c este cu

albastru vectorii a b și d c sunt

reprezentanți ai vectorului am

apoi vectorii sau segmentele orientate

a d și b c sunt reprezentanți ai

vectorului b iar vectorii a e b

f și c g sunt reprezentanți ai

vectorului c spuneam mai devreme

că adunarea vectorilor este comutativă

Așadar a plus b este egal cu b

plus a Haideți Să arătăm și pe

figura acest lucru mai întâi adunăm

vectorii a și b vom considera doi

reprezentanți a acestora și anume

adunăm vectorii a b și b c nu folosi

regula triunghiului Așadar suma

acestor doi vectori va fi vectorul

ac pentru a aduna a vectorii b

și a vom lua în considerare alți

reprezentanți ai acestora pentru

a putea aplica regula triunghiului

vom aduna vectorii a de și de Ce

observăm că dacă folosim regula

triunghiului pentru a aduna acești

doi vectori obținem același Vector

sumă AC am arătat Așadar cu operația

de adunare a vectorilor este comutativă

Haideți Să arătăm că această operație

este asociativă vrem Să arătăm

că vectorul a adunat cu vectorul

b plus c este același lucru cu

a plus b adunat cu c pentru a adunat

mai întâi vectorii b și c vom aduna

reprezentanții acestora b c și

c d Folosind regula triunghiului

iar vectorul sumă va fi vectorul

b g acesta este suma vectorilor

b și c Și acum trebuie să adunăm

vectorul a cu această sumă adunăm

de exemplu vectorul ab cu bc și

Folosind regula triunghiului obținem

vectorul Age acesta va fi suma

vectorilor a b și c și acum vrem

să verificăm dacă adunând vectorii

a b și c în acest mod obținem același

Vector Haideți să adunăm acum vectorii

a și b cu vectorul c observăm că

avem deja suma vectorilor a și

b acesta este vectorul AC mai trebuie

să adunăm acest Vector cu vectorul

c Așadar vom aduna vectorul AC

cu cg Folosind regula triunghiului

obținem a g Așadar observăm că

același Vector a g este și suma

vectorilor a plus b plus c Adunați

în acest mod am arătat astfel că

adunarea vectorilor este asociativă

și o altă proprietate era existența

elementului opus Haide să vizualizez

și această proprietate avem vectorul

a și opusul acestuia în minus a

vă reamintesc că doi vectori sunt

opuși dacă au aceeași direcție

aceeași mărime dar sensuri opuse

pentru a aduna acești doi vectori

după regula triunghiului ar trebui

să așezăm vectorul minus a cu originea

în extremitatea primului Vector

Deci punctul B prim ar coincide

cu punctul B Dar cei doi vectori

au aceeași mărime prin urmare și

punctul a prim coincide cu punctul

A ca să adunăm cei doi vectori

după regula triunghiului ar trebui

să unim originea a primului Vector

adică punctul A cu extremitatea

celui de al doilea Vector așa Dar

ar trebui să unim punctele a și

a prim care coincid Așadar adunând

CD Vector obținem vectorul nul

prin urmare să reținem că orice

Vector a are un opus notat cu minus

a iar adunând acești doi vectori

se obține vectorul nul în secvența

următoare mă face câteva exerciții