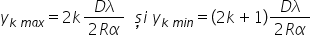Alte interferometre cu interferenţă nelocalizată: Lloyd şi Fresnel.

În ce dată iau lecție de optică

ondulatorie am discutat despre

interferometrul a Lloyd shiffrin

oglinda lui oiță interferometrul

Lloyd obține unde coerente prin

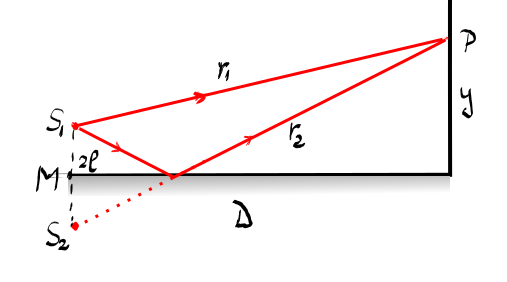
reflexie pe oglinda așa cum se

vede în această schemă și anume

avem o sursă S1 ce emite o rază

de lumină care se reflectă pe oglinda

orizontală desenată cu culoarea

albastru deschis unde le si vin

direct sau razele si vin direct

de la sursa S1 vor interfera cu

razele ce vin de la sursă S1 prin

reflexie ele vin ele parcă ar veni

din sursa imagine ASUS S1 glynne

Dar bineînțeles această sursă s

2 Stem una virtuală fiind format

între oglindă plan esențialul în

acest tip de dispozitiv sunt două

lucruri în primul rând faptul că

cele două unde cea directă și cea

prin reflexie sunt coerente deoarece

au aceeași pulsații aceeași frecvență

pentru că în fenomenul de reflexie

a undelor nu se schimbă frecvența

sau pulsația unde deci unde is

1 pe și unde S1 să notăm acest

punct cu qs1 cupe vor avea aceeași

frecvență Deci vor știi pe cel

de al doilea lucru Important este

că în fenomenul de reflexie avem

o pierdere de semiunda am discutat

despre acest lucru în lecțiile

de unde mecanice și anume am spus

că atunci când o undă este reflectată

pe un mediu cu indice fracție mai

mare sau după cum discutam acolo

Dacă aveam un nod la suprafața

de reflexie atunci are loc o pierdere

de ciment acesta este cazul dispozitivului

Lloyd pentru că indicele de refracție

al oglinzii care făcută din sticlă

e mai mare decât cel al Deci în

acest punct avem o pierdere de

semi un de pe care va trebui să

o luăm în considerare când calculăm

diferența de drum Optic între cele

două raze ce ajung în punctul p

și anume roz aerul 1 de lungime

1 S1 p și raza de lungime r2 s1q

pe care este egal cu F2 pe deoarece

s1q este egal cu F2 Deci dorim

să calculăm franjele de interferență

pe ecranul e vertical prin suprapunerea

celor două unul S1 S2 distanță

S1 S2 inota tăcu 2 L și poziția

punctului pe pe ecranul vertical

față de axa dispozitivului Care

este Care coincide cu oglinda cu

notăm cu y Alfa foarte mic tangent

de Alfa este egal cu alfa Deci

G egal cu deal de asemeni putem

scrie că Delta EUR este egal cu

F2 n minus Land apele De ce Haide

să discutăm această parte importantă

ecuație În primul rând minus la

am dat pe 2 datorită pierderii

de semiunda la refflex trebuie

să ținem cont că în momentul flexiei

undă reflectată pierde această

distanță Lambda pe doi Deci 3 iar

Delta aer este aproximativ egale

cu s2m De ce spun aproximativ egale

cu rest 2 n pentru că pentru a

fi foarte exact de stire adică

iar 2 minute ru nu este următoarea

distanță trasăm un cerc cu raza

R1 cu centrul în b și raza R1 ce

trece prin S1 și atunci R1 va fi

distanța dintre pe și acest punct

în concluzie exact Vorbim vorbim

foarte precis Delta aer va fi S2

distanța dintre S2 și acest punct

Dar pentru valori Alfa foarte mici

nicicând dacă vă imaginați Alfa

devenind din ce în ce mai mic Ce

se întâmplă atunci este că pe Se

apropie foarte mult de axa S1 S2

devine foarte mic și el și atunci

practic dreptele r s 1p pe m și

pe S2 din să coincidă în acel caz

acest punct Se apropie foarte mult

de an și Deci Delta Air devină

aproximativ egal cu F2 în concluzie

Delta Air va fi aproximativ egale

în această limită Alfa foarte mic

cu s 2-a minus lemne pe 2 nu mai

demonstrez de ce Pentru că am făcut

Open lecția trecută pentru dispozitivul

Young Dar acest unghi S2 n este

egal cu unghiul Alfa și în concluzie

Delta s2n va fi 2 L adică S1 S2

înmulțit cu sinus de Alfa în concluzie

putem scrie că Delta aer este egal

cu 2 L Alfa pentru Alfa foarte

mic sinus de Alfa este aproximativ

egale cu alfa zici aproximativ

egale cu alfa minus lemne pe 2

Dar Alfa poate fi extras din această

ecuație și obținem că Delta aer

este 2 L înmulțit cu alfa Care

este împărțit la d minus Vanda

pe doi în lecția trecută am stabilit

că franjele luminoase adică de

intensitate maximă se obțin pentru

Delta l egal cu multiplu par de

la 2 înlocuind în această ecuație

rezultă că franjele luminoase se

obțin în aceste poziții multiplu

impar de de lemn de împărțit la

4 iar și similar franjele întunecate

să obțin în poziții de el tire

egal cu multiplul impar de la îmi

dă pe 2 rezultă că franjele întunecate

de aici numele minim sunt la un

multiplu par de la de de de de

la împărțit la 4 L se observă că

distribuția franjuri lor a inversă

față de dispozitivul Young adică

avem maxim la multiple impare și

nu pare și invers pentru cele întunecate

Dar și asta se întâmplă datorită

faptului că avem o pierdere de

semi unde prin reflexie Deci felul

în care se obțin Unde coerente

În oglinda sau interferometru Lloyd

este prin reflexie și nu prin separare

iar prin reflexie avem această

pierdere de semyon de ceea ce duce

la inversarea flanșelor luminoase

și întunecate vizavi dispozitivul

ia si oglinzi lenel sunt tot ovariene

oglinzilor Lloyd dar în care folosind

două oglinzi în loc de una la se

obțin Unde coerente tot prin reflexie

dar pe două grinzi ce fac unui

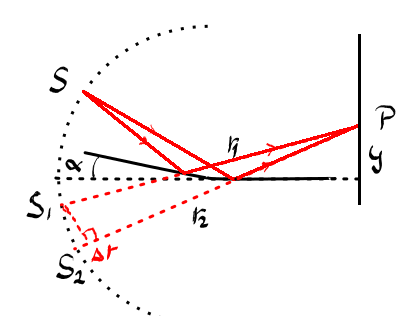
Alfa foarte mic schema este următoarea

Deci avem o sursă de lumină s și

două oglinzi desenate cu albastru

deschis și un ecran ceea ce se

întâmplă este că vom forma 2 imagini

de data aceasta pentru sus se ia

o imagine S1 față de prima oglindă

deci pur și simplu avem un S1 la

distanță egală față de oglinda

de prima glinda Deci această distanță

este egală cu aceasta și la fel

avem un sursă s 2 Față de cea de

a doua oglindă nici pe planul cele

de a doua glinde Care este albastru

întrerupt aici NASA nostru vom

avea un S2 amândouă sunt sursei

imaginare unghiul din nou dintre

planele celor două baze este Alfa

și este foarte mic în acest dispozitiv

prin această construcție os s o

va fi egal cu os 1 și la fel somn

este egal cu os 2 datorită faptului

că distanțele distanța lui S1 față

de prima oglindă egal cu distanța

lui esti față de prima oglindă

la fel și pentru cea de a doua

d și rezultă că avem această egalitate

dacă notăm cu r distanța om o fiind

vârful celor două oglinzi Deci

punctul de intersecție a celor

două linii atunci rezultă că cele

trei surse una reală și două imaginare

se află pe un cerc de aceasta Iar

pentru valori foarte mici a lui

Alfa distanța dintre S1 S2 este

această rază r înmulțit cu el Haide

să vedem cum se formează interferența

pe ecranul vertical în acest caz

desenul este complicat Dar ideea

este relativ simplă și anume că

avem la 10:00 pornesc din sus are

ala este reflectă pe prima oglindă

și alte raze se reflectă pe cele

2 oglindă ele suprapuse în poziția

ecranului și formând în felul acesta

interferențe Vrem să vedem unde

avem franjuri miroase și întunecate

ca de obicei ceea ce înseamnă că

vrem să calculăm di Florența de

drum Optic între două raze ajung

în același punct A În cazul acesta

dorim să calculăm diferența S2

pe minus s1p Deci avem un aer 1

este egal cu S1 p și r 2 este egal

cu s2p și dorim să calculăm diferența

de drumul Optic r 2 minus 1 și

apoi putem ca impune condiția de

maxim și de minim două comentarii

În primul rând Bineînțeles că avem

și ai pierderi de semiunda dar

pierdere de la nunta pe 2 Dar asa

perdele de la am dat pe doi se

întâmplă pentru amândouă undele

pentru că amândouă undele ce ajung

în pe sunt reflectate și în concluzie

când facem diferența această pierdere

de semi unde se va simplifica altfel

spus ar trebui să scriu Air 1 este

egal cu s1pe minus Vanda pe 2 r

2 este egal cu S2 pe minus la am

dat pe 2 pentru a ține cont de

aceste pierderi de secundă dar

oricum noi suntem interesați în

aer 2 minute R1 și acest minus

Lambda pe doi se va simplifica

si asa este primul comentariu al

doilea comentariu este că bineînțeles

undele reale razele de lumină sunt

pe vin din nu din S1 și S2 dar

geometric vorbind putem folosi

S1 pentru că ies o este egal cu

a Sano sau dacă notăm punctul de

incidență de aici cu i s este egal

cu al unui bun cu aceste comentarii

să calculăm în primul rând notăm

cu y poziția ca și până acum igrec

este poziția punctului p față de

axa sa de simetrie a dispozitivului

ce trece prin mijlocul distanței

S1 S2 Deci acesta este chiar acesta

va fi d distanța dintre planul

surselor S1 S2 și ecran și Deci

nu tin cu teta pentru că am folosit

Alpha deja notăm cu tete acestui

unghi și deci ys3d cu dettingen

de tata pentru valori mici a lui

tata ceea ce se întâmplă când Alfa

este mic este egal cu dor te asemeni

Delta R este egal cu S1 S2 înmulțit

cu tata demonstrația este identică

Deci nu voi insista asupra ei ca

pentru celelalte interferometrie

Young și Lloyd și anume Delta l

este acest este s 2-a minus S2

pe minus s1pe și este acest segment

iar acestui unghi este egal cu

teta Deci rezultă că sinus de teta

este Delta aer pe S1 S2 Dar pentru

valori mici el uite tusin de tata

este tentat deci de tare este S1

S2 muzicute înlocuind S2 în această

ecuație obținem că y este egal

cu Doar tata Care este Delta este

egal cu Delta Air împărțit la r

l Deci y10a punctului p este de

împărțit la R Alfa mulți cu diferența

de drum de el tire iar la acest

punct putem imediat calcula acest

moment în demonstrație putem calcula

poziția franjuri lor luminoase

și întunecate punând condiția ca

Delta aer să fie un multiplu par

de semi unde obținem franjele luminoase

Deci poziția francilor luminoase

va fi multiplu parc de doi de de

la împărțit la 2 aer Alfa iar acelor

întunecate la o multiplu impar

de de lemn de împărțit la 2 r a

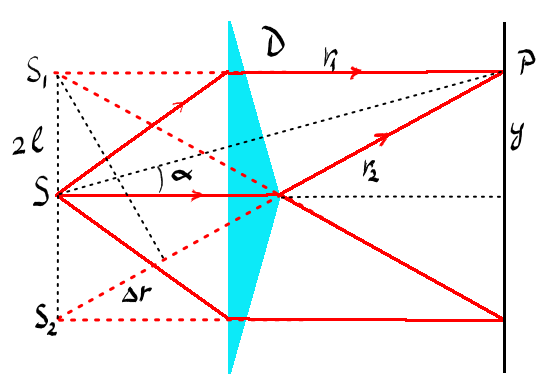
flanel a introduci un alt interferometru

numit biprisma fresnel care obține

unde coerente prin de refracție

nu prin reflexie între o prismă

cu un unghi a foarte Micu unghiul

A este unghiul de la baza Deci

acesta este unghiular egal cu acesta

a acestuia este foarte bine Și

atunci Unde le ce pleacă din sursa

s se vor reflecta și transmite

către ecranul vertical bineînțeles

Care fracție este mai complicată

liniile razele sunt mai complicate

în interior decât am desenat eu

dar pentru unghiuri a foarte mici

putem neglija direcția din segmentele

razelor de lumină din interiorul

prismelor pentru că le sunt foarte

scurte Deci Considerăm numai prima

refracție și bineînțeles dorim

să calculăm ce se întâmplă în punct

pe Adică dacă obținem franjele

luminoase sau întunecate întru

un punct pe aflat pe ecran la o

poziție y unde notăm din nou cu

d distanța dintre sursa s și ecran

ceea ce se întâmplă este că franjele

care se formează prin suprapunerea

undelor pot fi considerate ca provenind

de la imaginile virtuale sunt și

S2 Deci bine refracție și prelungind

razele refractate obținem poziția

unei sursei imaginar S1 format

în prima prisma Abi prismei și

o sursă imaginară S2 formată în

cea de a doua prismă a prismei

cea de jos după cum vedem avem

prelungirile a două raze formate

prin refracție prima prismă se

întâlnesc și formează o sursă sau

o imagine a sus numita S1 și la

fel S2 pentru a calcula franjele

luminoase scrie notăm S1 S2 distanța

S1 S2 cu 2 L poziția punctului

p față de axa dispozitivului cu

y și d distanța dintre planul surselor

și ecranul e iar cu alfa unghiul

cu care neam obișnuit deja până

acum demonstrație este identică

de la punctul acesta cu cea pentru

dispozitivul Young Deci voi trece

foarte pe scurt peste ecuație ele

sunt identice deci putem scrie

că ys3f Roxi motiv egal cu Dorel

fă Deci y este de înmulțit cu tangent

de Alfa Dar el fie foarte mic Deci

egal cu alfa de asemeni putem scrie

că Delta Air care pentru punctul

p este egal cu F2 pe minus s1p

Deci ne uităm la cele două surse

și la punctul p și Delta l este

diferența de drum Optic dintre

razele ce vin de la cele două surse

Deci Delta Air este s2p minus s1pe

și el va fi egal cu s2n ce discuții

aproximativ egale cu s2n numai

explicată aproximații refăcute

revedeți discuția din cazul oglinzi

Lloyd sau din cazul interferometru

lui Young Care este aproximativ

egală din nou cu 2 L sinus de Alfa

adică 2L Alfa înlocuind Alfa din

cele două ecuații obținem ecuația

cunoscută Spre exemplu pentru dispozitivul

Young și anume că y este aproximativ

egal cu d împărțit la 2 l înmulțit

cu Delta Air în care putem pune

condiția de fragi luminoase sau

întunecate și obținem Evident ecuația

fiind aceleași obținem aceleași

poziții ale frazelor luminoase

și întunecate ca și în dispozitivul

ea în concluzie prisma flanel obține

aceeași distribuția flanșelor ca

și în cazul dispozitivului Young

ecuațiile sunt identici mecanismul

de obținere a unde de interferență

este diferit Nu separăm unde ai

inițială obținem două unde coerente

prin separare ca în cazul dispozitivului

și prin refracție