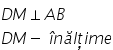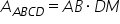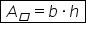Aria paralelogramului

în această lecție o să deducem

formula de calcul pentru aria paralelogramului

vă reamintesc că un paralelogram

este un patrulater cu laturile

opuse paralele se dă mai întâi

o definiție se numește înălțime

a unui paralelogram perpendiculara

dintre un vârf al paralelogramului

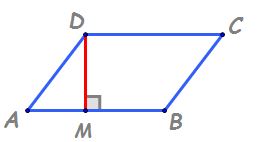
pe latura opusă am duce perpendiculară

din D pe latura ab dm va fi înălțimea

acestui paralelogram a fi putut

duce și perpendiculara din D pe

latura bc pentru a putea deduce

formula de calcul pentru aria paralelogramului

o să construim o diagonală a acestui

paralelogram ducem diagonala bd

observăm că sau format două triunghiuri

triunghiurile ABD și cbd observăm

că aceste două triunghiuri sunt

congruente conform cazului de congruență

latura latura latura ele au o latură

comună aceasta este diagonala bd

știind că între un paralelogram

Laturile opuse sunt congruente

două câte două Deci a b va fi congruentă

cu dc iar AD va fi congruentă cu

bc mai putem observa de asemenea

că aria acestui paralelogram se

obține însumând ariile celor două

triunghiuri scrie că triunghiul

adb este congruent cu triunghiul

cbd conform cazului de congruență

latura latura latura Și de aici

va rezulta că Aria triunghiului

adb este egală cu aria triunghiului

c b d pentru că două triunghiuri

congruente au ariile egale mai

putem scrie că aria paralelogramului

a b c d este compusă din aria triunghiului

adb plus aria triunghiului cbd

dar având în vedere că aceste două

arii sunt egale Putem să scriem

din aceste două relații că aria

paralelogramului a b c d a fi egală

cu 2 ori aria triunghiului adb

adb este un triunghi oarecare iar

aria unui triunghi oarecare se

obține după formula baza ori înălțimea

supra 2 baza acestui triunghi este

ab adică latura pe care am dus

înălțimea Așadar vom scrie egal

cu 2 ori ab ori de m supra 2 se

simplifica 2 cu 2 și obțin m egal

mai departe cu AB ori dm a b poate

fi numită baza paralelogramului

iar de m se va numi înălțime Deci

formula de calcul pentru aria paralelogramului

în general este baza ori înălțimea

mama aplica această formulă rezolvare

a exercițiilor și problemelor în

continuare să facem o problemă

Un paralelogram abcd are latura

ab de 24 cm și distanța de la C

la AB egală cu 10 cm Calculați

aria paralelogramului după cum

am văzut mai devreme Aria unui

paralelogram este baza ori înălțimea

în acest paralelogram înălțimea

este cm iar baza paralelogramului

este latura ab adică latura pe

care a construit perpendiculara

m scrie că aria lui a b c d este

baza a b ori înălțimea cm egal

cu 24 ori 10 egal cu 240 cm pătrați