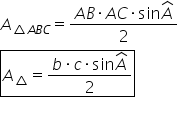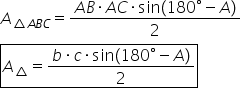Aria triunghiului folosind sinusul
Tag-uri
Partajeaza in Google Classroom
Transcript
în această lecție o să deducem
o formulă de calcul pentru aria
unui triunghi folosind funcția
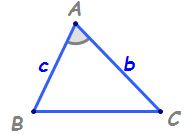
trigonometrică sinus avem un triunghi
oarecare a b c în care am duce
înălțimea AD știind că aria unui
triunghi în general este baza ori
înălțimea supra 2 în acest triunghi
bază este bc iar înălțimea este
Ade egal cu bc ori ad supra 2 triunghiul
ABD este un triunghi dreptunghic
exprimă sinus de B în acest triunghi
În triunghiul dreptunghic ABD sinus
de B este raportul dintre cateta
opusă unghiului B adică ad și potenza
ab din această relație o sa exprimi
lungimea segmentului ad aceasta
va fi egală cu AB ori sinus de
b și locuim această relație în
formula ariei scrisă mai sus astfel
din cele două relații obținem că
aria triunghiului este egală cu
bc în loc de Adi o să scriu Am
ori sinus de b totul supra 2 observăm
Așadar că aria unui triunghi oarecare
va fi egală cu produsul a două
laturi a b ori b c ori sinusul
unghiului dintre ele supra 2 această
formulă este valabilă pentru triunghiul
ascuțit unghic în acest caz măsura
unghiului b este mai mică de 90
de grade Să vedem acum care va
fi formula de calcul pentru aria
triunghiului în cazul în care unghiul
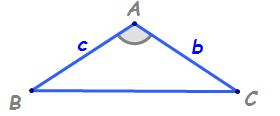
b este un unghi obtuz avem un triunghi
abc obtuzunghic din acest motiv
înălțimea dusă din a va fi situat
în exteriorul triunghiului să exprimăm
măsura unghiului ABD observăm că
măsura unghiului ABD va fi egală
cu 180 de grade minus măsura unghiului
abc Putem să scriem pe scurt 180
de grade minus b unde prinde înțeleg
unghiul abc în triunghiul dreptunghic
adb și exprimăm sinusul unghiului
ABD sinusul este raportul dintre
cateta opusă și ipotenuză cateta
opusă unghiului ABD este ad iar
ipotenuza este ab egal cu ad supra
ab o să exprimi în această relație
lungimea înălțimii ad va fi egală
cu AB ori sinusul unghiului ABD
Dar cum unghiul ABD este 180 de
grade minus b obținem astfel ab
ori sinus de 180 de grade minus
b aria triunghiului este baza ori
înălțimea supra 2 adică bc ad supra
2 egal cu bc ori în loc de Adi
o să scriem ab ori sinus de 180
de grade minus b totul supra 2
am obținut astfel formula de calcul
pentru aria triunghiului în cazul
în care unghiul b este obtuz în
continuare o să facem o aplicație
anul scris formula de calcul pentru
aria triunghiului ascuțitunghic
aceasta este egală cu produsul
a două laturi ori sinusul unghiului
dintre ele supra 2 și avem următoarea
problemă Se dă un triunghi ABC
se știe că ab este 4 radical din
3 AC este 5 radical din 3 și măsura
unghiului a este egală cu 30 de
grade se cere sa calculăm aria
triunghiului ABC a folosi aceleași
desen știind că a b este 4 radical
din 3 AC este 5 radical din 3 și
măsura unghiului a este egală cu
30 de grade aplicăm această formulă
aria triunghiului ABC va fi egală
cu AB ori ac ori sinus de a supra
2 egal a b este 4 radical din 3
AC este 5 radical din 3 și măsura
unghiului a este de 30 de grade
ori sinus de 30 de grade supra
2 egal 4 ori 5 este 20 radical
din 3 ori radical din 3 este 3
și sinus de 30 de grade este 1
pe 2 totul supra 2 egal putem să
simplificăm 20 cu 2 mai rămâne
10 10 ori 3 este 30 pe 2 egal cu
15 cm pătrați
Aria triunghiului folosind sinusul unui unghiAscunde teorie X
Navigare în lectii
Cumpara abonament
