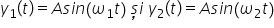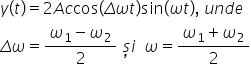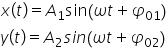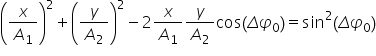Bătăile. Compunerea oscilaţiilor perpendiculare.
Tag-uri
Partajeaza in Google Classroom

Transcript
în cele 4-a lecții despre oscilații
și unde mecanice vom discuta despre
fenomenul de bătăi și apoi despre
compunerea oscilațiilor perpendiculare
bătăile se obțin la compunerea
oscilațiilor armonice paralele
cu frecvențe diferite dar apropiat
am discutat despre compunerea oscilațiilor
armonice paralele în lecția trecută
și vom discuta acuma despre cazul
particular al comportării acest
ecuațiilor obținute în cazul în
care Delta Omega este mult mai
mic decât Omega vom redefini imediat
acești parametri care au fost definiție
în lecția trecută Considerăm cazul
simplu al atitudinilor egali Deci
după cum spuneam în lecția trecută
am Demonstrați că în cazul a 25
armonice paralele elongația oscilații
compuse Y6 de timp este egală cu
dublul amplitudinii comune acelor
25 individuale înmulțit cu cosinus
de Delta omega-3 și sinus de Omega
taie unde de al tau negativ a fost
definit ca jumătatea diferenței
dintre pulsație individuale ale
celor 25 paralele iar Omega k jumătatea
sumei celor două pulsații pentru
a vedea ce se întâmplă în în acest
caz particular în care cei doi
parametri sunt relaționate în felul
acesta să Reprezentăm grafic această
funcție pentru două valori ale
pulsațiilor Omega 1 și omega 2
care îndeplinesc această condiție
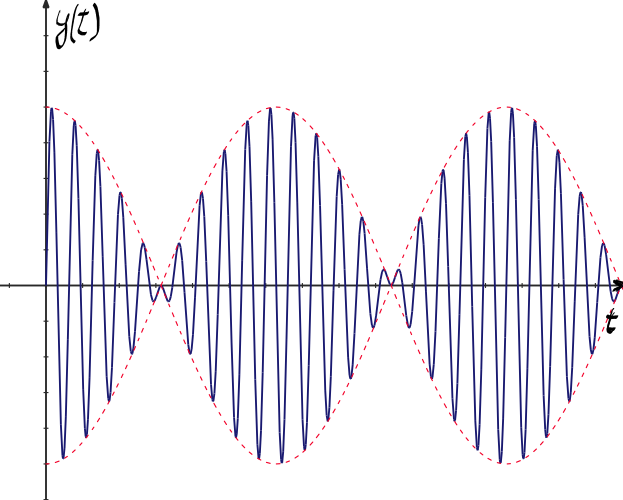
De ce vedeți în acest grafic cu
albastru este de t de inundația
oscilației compuse în după această
formulă iar cu roșu amplitudinea
a reprezentată de termenul din
fața funcției sinusoidale sinus
de omega-3 adică 2-a cosinus de
Delta Omega am ales două valori
ale pulsațiilor individuale Omega
1 și omega 2 astfel încât diferența
jumătatea diferenței să fie mult
mai mică decât jumătatea sumei
Deci pentru aceste două frecvențe
obținem în Delta Omega de 2 hărți
și unul Mega de 20 de hărți de
10 ori mai mare ce vedem ca atunci
oscilația compusă are o dependență
sinusoidală periodică dar și altitudinea
ei Care este această funcție se
înscrie într o anvelopă Care este
periodică dar cu o perioadă mult
mai mare acest tip de dependență
temporală a unei oscilații se numește
bătăi Deci bătăile sunt oscilații
de pulsație Omega cu albastru întru
anvelopă oscilantă de pulsație
Delta Omega unde Omega este mult
mai mare decât Delta Omega ceea
ce înseamnă că perioada bătăilor
care sunt această anvelopă înscris
în această anvelopă cu roșu punct
întrerupt perioada bătăilor este
mult mai mare decât perioada oscilației
în sine să trecem acum la compunerea
oscilațiilor perpendiculare oscilațiile
perpendiculare apar atunci când
o și la torul este legat la 25
la ții a produse de forțe la Stitch
cu direcții perpendiculare ca acest
desen Deci Omega 1 este egal cu
Omega 2 Considerăm acest caz particular
ceea ce înseamnă că cele două resorturi
au constante elastice egale și
atunci putem scrie orice la țiile
individuale produse de cele două
resorturi x data este A1 sinus
de omega-3 plus și 01 de ten este
a 2 sinus de omega-3 plus și 02
ce dorim în următorul calcul trigonometric
este să eliminăm dependența de
Omega de timp și să obținem o dependență
directă între x și y în acest caz
însă cele două elongații procedăm
1 prin desfacerea argumentului
acestor două funcții mai exact
folosind următoarea identitate
trigonometrică sinus de Alfa Beta
este egal cu sinus de Alfa cosinus
de beton plus cosinus de Alfa sinus
de beata Deci desfăcând folosind
această relație trigonometrică
desfăcând aceste funcții sinusoidale
obținem aceste Două ecuații pentru
x și y apoi procedăm în felul următor
mulțimi prima ecuație cu cosinus
de phi 2 și 0 2 și a doua cu sinus
de pi zero doi motivul fiindcă
procedând în felul acesta primul
termen al adunării din dreapta
egalului devine egal Deci vom ține
termeni egali în această parte
a ecuațiilor și apoi scăzând le
obține următorul următoarea relație
x împărțit la 1 cosinus de fi 0
2 minus y împărțit la 2 cosinus
de fie 0 fie zero unu trebuia să
spun aici Deci cosinus de fi 0
1 De ce mă țin chiar a doua ecuații
cu cosinus de fi 01 așa este egal
cu prin scădere observăm că primul
termen se simplifică de sinus de
omega-3 cosinus de fie 01 cosinus
de fie zero doi va fi termenul
în ambele ecuații de sus și de
Jos Deci se simplifică prin scădere
și apoi scăzând și îi dai termenii
numărul 2 din adunare obținem cosinus
de Omega tem sinus de fi 01 02
minus sinus de 0 2 cosinus de 0
1 dar această diferență este egală
cu această diferență este egală
cu sinus cu minus sinus de fi 0201
deci putem scrie în continuare
această relație în care după cum
am spus expresia din paranteză
este minus sinus de fi 0 în următoarea
etapă a demonstrației înmulțim
aceleași 2 Quad ții cu sinus de
0 2 prima și sinus de 0 1 cl a
2-a motivul fiind acela și de data
aceasta termenii numărul 2 din
adunare se vor se simplifica la
scădere Deci obținem x împărțit
la 1 sinus de 0 2 minus y împărțit
la a 2 sinus de fi 01 va fi egal
cu sinus de omega-3 factorul comun
înmulțit cu cosinus fie zero unu
și zero doi minus cosinus de fi
0 2 sinus de fie zero unu care
este egal cu sinus de fie zero
doi minus și zero unu din nou termenii
numărul 2 din sumă în se simplifică
fiind identici după această înmulțire
De ce au obținut aceste două relații
reamintesc scopul nostru este eliminarea
acestor doi termeni și observăm
că dacă ridicăm la pătrat și adunăm
vom obține cosinus pătrat plus
sinus pătrat acești doi termeni
fiind identice de cinci ori la
ce putem elimina cele două dependențe
temporale Deci din nou înmulțim
ridicăm la pătrat ambele ecuații
și le adunăm reamintesc că avem
următoarea relație a plus b sau
a minus d vom folosi a minus b
la pătrat este egal cu a pătrat
plus b pătrat minus 2-a b Bun deci
ridicăm la pătrat și obținem la
următorul lucru x pătrat împărțit
la 1 la pătrat cosinus pătrat de
fi 02 asta din prima ecuație din
a doua obținem x pătrat împărțit
la 1 la pătrat sinus de fie zero
doi apoi termenii al doilea numărul
2 y pe trat împărțit la a 2 la
pătrat cu sinus la pătrat de fie
zero unu plus y pătrați împărțit
la a 2-a 2 la pătrat sinus la pătrat
de fi 0 1 apoi termenii de tipul
2-a b minus 2 x împărțit la 1 y
aceasta este ce obținem din adunarea
pătratelor din stânga egalului
iar din dreapta egalului după cum
am spus obținem cosinus la pătrat
bagat plus sinus la pătrat de Omega
ten tuturor munții cu factorul
comun la pătrat sinus pătrat de
și 0 2 minus și 0 1 5 este important
de observat este că cel mai important
fapt este că acest termen Care
este singurul dependent de timp
devine egal cu 1 și apoi de asemeni
observăm că avem termen de tipul
alți termeni de tipul cosinus a
pătrat plus sinus la pătrat Spre
exemplu acest termen va fi egal
cu x pătrat împărțit la 1 la pătrat
la fel acest termen această parte
a va fi egală cu pătrat împărțit
la al doilea pătrat în concluzie
obținem următoarele ecuații x pătrat
împărțit la 1 la pătrat plus pătrat
împărțit la 2 la pătrat plus această
acest termen va fi egal cu termenul
din dreapta unde din nou acest
termen este egal cu 1 acestor Man
este egal cu cosinus de pi zero
doi minus fie zero unu și definind
următorul următoarea mărime Delta
fi 0 prin definiție fie zero doi
este fie zero doi minus cinci zero
unu obținem ecuația finală între
x și y Deci obținem că x împărțit
la 1 la pătrat plus y împărțit
la 2 la pătrat minus doi x împărțit
la 1 împărțit la 2 cosinus de Delta
fi 0 este egal cu sinus la pătrat
de Delta fi 0 În care din nou eliminat
dependența temporală și avem o
relație directă între locațiile
celor două oscilații perpendiculare
x și y Aceasta este o ecuație generalizată
a X a adică Ea este o elipsă cu
un anumit unghi de înclinare în
planul x y dat de Delta fie 0 avem
următoarele cazuri particulare
oscilații eliptic m apar atunci
când Delta e 0 este multiplu de
pi pe 2 când Delta fi 0 este un
multiplu de pipe 2 cosinus de Delta
fi 0 devine egal cu 0 Deci acest
termen dispare în întregime iar
sinus de Delta fi 0 devine egal
cu plus sau minus unu care la pătrat
este egal cu 1 judeci obținem acest
tip de ecuație în cazul și mai
particular în care A1 este egal
cu a 2 cele 25 iau amplitudine
egale obținem 25 la ție compusă
circular x pătrat plus pătrat egal
cu a pătrat aceasta este ecuația
unui cerc scuzați următoarea următorul
caz particular este cel al usilor
în față în care Delta fi 0 este
multiplu par dep în acest caz sinusul
devine egal cu 0 și cosinusul devine
egal cu plus 1 Și de ce obținem
x pătrat împărțit la 1 la pătrat
plus y pătrat împărțit la a 2 la
pătrat minus 2x pe A1 yii2 egal
cu 0 acesta această relație este
echivalentă cu x împărțit la 1
minus igrec împărțit la a 2 totul
la pătrat egal cu 0 Deci grec este
egal cu A2 plus împărțit la 1 împărțit
la înmulțit cu x y egal cu a 2
împărțit la 1 nu ții cu X mici
obținem o simplă oscilație liniar
ușa torul compus va avea voce Pe
o dreaptă iar oscilațiile nu poziție
de fază în care Delta fie 0 este
egal cu un multiplu impar de pe
corespunde cazului în care Delta
fi 0 este egal cu 0 sinus de Delta
fie 0 este egal cu 0 iar cosinusul
este egal cu minus 1 și în acest
caz obținem semnul minus în loc
de plus în această dependență liniară
ca și comentariu finalul aceste
oscilații compuse de tip paralel
sau perpendicular sau chiar și
mai complexe sunt folosite în varia
mașini în industriale Spre exemplu
vedeți un caz relativ simplu al
amortizoarelor de șocuri folosit
în folosite întruna automobil dar
chiar și în acest caz putem vedea
că sistemul de resorturi sau de
alte oscilatoare folosite pentru
amortizarea șocurilor din roată
este destul de complexe Ele pot
fi oscilații de tip pur mecanica
de exemplu în resort din oțel dar
pot fi și alte tipuri de uși la
toare Spre exemplu avem suspensie
telescopice suspensii pneumatice
dar toate execută mișcări mișcări
oscilatorii care sunt compuse în
așa fel încât să absorbim jocurile
din multi din mai multe direcții
asupra