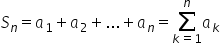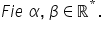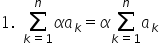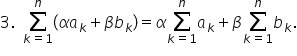Calculul unor sume și scrierea acestora cu ajutorul simbolului Sigma

de multe ori în matematică se utilizează

litere grecești litera grecească

Sigma se folosește pentru a scrie

mai ușor și pentru a calcula mai

rapid anumite sume dacă avem de

exemplu următoarea sumă notată

cu s n o sumă de n termeni de formă

a 1 plus A2 plus a 3 plus puncte

puncte plus a n această sumă se

poate scrie mai restrâns cu ajutorul

acestui simbol termenul general

al sumei este de formă a k unde

k aia valori de la 1 până la n

iar dacă scriem o față a termenului

general simbol Sigma pentru că

apa luni valori de la 1 până la

n obținem astfel o scriere mai

restrânsă a acestei sume citim

astfel suma din a k pentru k luni

valori de la 1 până la n sau sumă

din a k când copil valori de la

1 la n sau mai simplu sumă din

a k k de la 1 la n De exemplu dacă

avem următoarea notație suma din

k la a patra pentru k de la 1 la

n atunci avem o sumă în care termenul

general este de forma k la puterea

a patra iar pentru k egal cu unu

obținem primul termen al acestei

sume și acesta va fi unul la puterea

a patra pentru k egal cu 2 obținem

cel de al doilea termen al sumei

2 la puterea a patra și continuăm

cu trei la a patra și așa mai departe

ultima valoare pe care o poate

lua k este n Deci ultimul termen

al sumei se obține înlocuind pe

k n și avem and la puterea a patra

un alt exemplu suma din 3 supra

k pe lângă k plus unu pentru k

luni valori de la 1 până la n acesta

este termenul general al sumei

în cazul în care k este egal cu

unu obținem primul termen 3 supra

1 ori 1 plus 1 adică 2 plus pentru

k egal cu 2 obținem cel de al doilea

termen al sumei 3 supra 2 ori 2

plus 1 adică 3 Plus cel de al treilea

termen al sumei va fi 3 supra 3

ori 4 și așa mai departe ultimul

termen al sumei este 3 supra n

pe lângă n plus 1 închidem plu

suma din 1 supra 2k minus 1 pe

lângă 2 k plus 1 pentru k luni

valori de la 1 până la n înlocuind

în expresia termenului general

pe capacul 1 obținem primul termen

al acestei sume 1 supra 2 ori 1

minus 1 este unu ori doi ori unu

plus unu este 3 plus acum Înlocuim

pe k cu 2 și obținem cel de al

doilea termen al sumei 2 ori 2

4 minus 1 3 ori 2 ori 2 4 plus

1 5 plus k egal cu 3 2 ori 36 minus

1 5 2 ori 3 plus 1 7 și așa mai

departe ultimul termen al acestei

sume va fi 1 supra 2-a minus 1

pe lângă 2 ani plus 1 Iată Deci

că aceste sume se pot scrie restrâns

cu ajutorul acestui simbol iar

înlocuind pe k cu o anumită valoare

Putem să scriem orice termen al

sumei acest simbol are câteva proprietăți

importante pe care o să le ducem

în continuare dacă avem de exemplu

o sumă din Alfa ori a k pentru

că apa lung valori de la 1 până

la n unde Alfa este un număr real

diferit de 0 Deci o constantă care

nu depinde de K atunci această

sumă se poate scrie astfel Alpha

ori A1 plus Alfa ori A2 plus puncte

puncte plus Alfa ori a desfășurat

această sumă pentru k luni valori

de la 1 până la n în continuare

observăm că putem să dăm factor

comun pe Alfa și obținem Alfa pe

lângă A1 plus A2 plus și așa mai

departe plus a n dar această număr

impar on teză se poate scrie sumă

din a k pentru copil în valori

de la 1 până la n și atunci avem

în continuare egal cu alfa ori

suma din a k pentru KL în valori

de la 1 până la n cu alte cuvinte

atunci când avem o constantă în

cadrul unei sume această constantă

va trece în fața sumei o altă proprietate

avem sumă din a k plus BK pentru

că apa luni valori de la 1 și până

la n observăm că avem o sumă în

care termenul general este o sumă

de doi termeni pentru k egal cu

unu obținem primul termen al acestei

sume a 1 plus 1 plus pentru k egal

cu 2 obținem cel de al doilea termen

al sumei A2 plus B2 plus și așa

mai departe pentru că apa egal

cu n avem ultimul termen a n plus

b n adunarea este asociativă prin

urmare putem să asociem acești

termeni Cum dorim și o să scriem

în continuare egal cu a 1 plus

A2 plus puncte puncte plus a n

plus 1 plus 2 plus puncte puncte

plus bn egal această sumă este

de fapt suma din a k pentru ca

apa lung valori de la 1 până la

n și această sumă va fi sumă din

BK pentru că apa luni valor de

la unu până la and iată că suma

unei sume este egală cu suma sumelor

aceste două proprietăți pe care

le am scris conduc la o atria proprietate

pe care nu sunt mai de ducem dar

este imediată suma din Alfa ori

a plus b ori b k unde Alfa și Beta

sunt constante pentru k luni valori

de la 1 până la n se poate scrie

Alpha ori sumă din a k pentru că

apa de la 1 la n Deci Constanta

va trece în fața sumei iar suma

unei sume va fi egală cu suma sumelor

deci putem să scriem în continuare

plus b ori suma din BK când că

apa Avalor de la unu până la an

să reținem Așadar aceste trei formule

vei care să le mai citesc încă

o dată suma din Alfa ori a că apa

este egală cu alfa o sumă din apa

prin urmare Constanta trece în

fața sumei suma din apa plus b

k este egală cu suma din apa plus

suma din BK iar suma din Alfa ori

a k a plus b ori b k se poate scrie

egal cu al Faur sumă din a k plus

Betta o sumă din BK în continuare

să facem două exerciții avem următoarea

sumă notată cu sn 1 ori 2 plus

2 ori 3 plus 3 ori 4 plus puncte

puncte plus pe n pe lângă n plus

unu și dorim să găsim o formulă

de calcul pentru această sumă mai

întâi aș vrea să ne reamintim formulele

de calcul pentru suma primelor

n numere naturale respectiv pentru

suma pătratelor și suma cuburilor

primelor n numere naturale pe care

le am demonstrat prin inducție

matematică Iată cine trei formule

scrise cu ajutorul simbolului Sigma

1 plus 2 plus puncte puncte plus

n este sumă pentru că apa de la

1 la n din k Deci termenul general

al sumei este ca apa și această

sumă este egală cu n pe lângă n

plus 1 supra 2 suma pătratelor

primelor n numere naturale 1 la

a doua plus 2 la a doua plus n

la a doua se poate scrie sumă din

ca pătrat pentru k de la 1 la n

și aceasta este egală cu n pe lângă

n plus 1 pe lângă doi ani plus

1 supra 6 și 1 la a treia plus

2 la a treia plus puncte puncte

plus n la a treia și poate scrie

suma din k la a treia pentru k

de la 1 până la n și este egală

cu n pe lângă n plus 1 supra 2

totul la pătrat și acum Haideți

să scriem și noi această sumă cu

ajutorul simbolului Sigma nu scrie

suma din k pe lângă k plus unu

observăm că termenul general al

sumei este un produs de două numere

consecutive Deci avem k pe lângă

k plus 1 unde k Avalor de la 1

până la n putem să verificăm pentru

că apa egal cu unu avem unu ori

doi Deci primul termen pentru ca

apa egal cu doi avem doi ori trei

Deci al doilea termen și așa mai

departe înseamnă că am scris corect

formula termenului General pentru

această sumă acum această sumă

se poate scrie astfel sumă pentru

că apa lung valori de la 1 la n

din k la pătrat plus k am desfăcut

paranteza înmulțim pe k cu fiecare

număr din paranteză suma unei sume

este egală cu suma sumelor prin

urmare vom scrie suma din ca pătrat

pentru că apa de la 1 la n plus

sumă din k pentru k luni valori

de la 1 până la n este formule

sumă din cap pătrat este n pe lângă

n plus 1 pe lângă 2 ani plus 1

supra 6 iar suma din k este n pe

lângă n plus 1 supra 2 o să aducem

la numitor comun amplificăm cu

trei și obținem n pe lângă n plus

1 pe lângă 2n plus 1 plus 3 n pe

lângă n plus 1 totul supra 6 nu

ma din Oare o să dăm factor comun

pe n pe lângă n plus unu Deci avem

n pe lângă n plus 1 pe lângă 2n

plus 1 plus 3 totul supra 6 egal

n pe lângă n plus unu aici o să

avem doi n plus 4 și dă factor

comun pe 2 2 pe lângă n plus 2

totul supra șase simplificăm pe

șase cu doi și final o să obținem

n pe lângă n plus 1 pe lângă n

plus 2 totul supra 3 iată că am

obținut astfel o formulă de calcul

pentru această sumă ample în Game

plus 1 pe lângă n plus 2 totul

supra 3 mai facem încă un exercițiu

avem suma s n 1 ori 4 plus 2 ori

7 plus 3 ori 10 plus puncte puncte

plus n pe lângă 3 ani plus unu

nu scrie și această sumă cu ajutorul

simbolului Sigma și avem sumă din

k pe lângă 3 k plus 1 pentru că

apelând valori de la 1 până la

n putem să verificăm pentru k egal

cu 1 avem 1 ori 4 primul termen

pentru k egal cu 2 avem 2 pe lângă

3 ori 2 plus 1 adică 2.7 și așa

mai departe desfacem 64 intens

Înmulțind pe capacul fiecare număr

din paranteză și obținem suma din

trei K la pătrat plus k pentru

k lung valori de la 1:00 și până

la n acum desfacem această sumă

în două sume și putem să trecem

Constanta în fața sumei de ce o

să scriu egal cu trei ori sumă

din capela pătrat pentru că apa

de la 1 la n plus sumă din k pentru

k de la 1 până la n acuma plecăm

din nou formulele amintite mai

devreme suma din k la pătrat este

n pe lângă n plus 1 pe lângă 2

ani plus 1 supra 6 iar suma din

cap este n pe lângă n plus 1 supra

2 simplificăm cu 3 și o să obținem

n pe lângă n plus 1 pe lângă 2n

plus 1 plus n pe lângă n plus 1

totul supra 2 acum la numărător

o să dăm factor comun pe n pe lângă

n plus 1 totul pe lângă 2 n plus

1 plus 1 totul supra 2 egal cu

n pe lângă n plus unu în paranteză

dreaptă obținem 2 n plus 2 dă factor

comun pe 2 și ne rămâne n plus

1 totul supra 2 se simplifică 2

cu 2 și obțin a n pe lângă n plus

1 la pătrat Iată Deci că am obținut

și în acest caz o formula de calcul

pentru această sumă lăsăm ca și

exercițiu demonstrație acestor

formule prin metoda inducției matematice