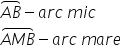Cercul- definiție, elemente
Tag-uri
Partajeaza in Google Classroom
Transcript
în această lecție o să discutăm
despre cerc o să vedem de finitie
acestuia elementele cercului și
notații fie o un punct în plan
și un număr pozitiv mulțimea tuturor
punctelor din plan situate la aceeași
distanță față de punctul o se numește
cerc de centru o și rază r avem
un punct fix o și un alt punct
situat la distanță R față de punctul
O observăm că putem să construim
o infinitate de astfel de puncte
situate la aceeași distanță R față
de punctul O dacă o să unim Toate
aceste puncte obținem cercul de
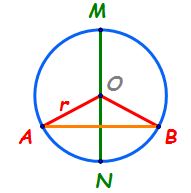
centru o și rază r să vedem mai
exact ce este raza cercului distanța
de la centrul cercului la un punct
situat pe cerc se numește raza
de exemplu segmentul o a este o
rază în acest cerc putem să mai
construim și un alt exemplu om
toate razele unui cerc au aceeași
lungime o altă definiție segmentul
care unește două puncte de pe cerc
se numește coardă punctele a și
m sunt situate pe cerc iar segmentul
a m se va numi coardă o coardă
care trece prin centrul cercului
se numește diametru de exemplu
BC este diametru pentru că segmentul
BC trece prin punctul O dacă ne
uităm la acest diametru observăm
că oc și ob sunt raze înseamnă
că lungimea diametrului va fi dublul
razei Putem să scriem astfel că
diametrul este egal cu 2 r diametrul
este cea mai mare dintre coardei
continuăm cu o altă definiție porțiunea
dintre un cerc determinată de două
puncte situate pe cerc se numește
arc de cerc porțiunea mai îngroșată
de pe acest cerc situată între
punctele a și b se va numi arcul
ab aceasta este notația pentru
arc însă observăm că punctele a
și b mai determină un arc este
vorba despre arcul desenat cu verde
punctat Acesta este un arc mare
pentru a face distincția între
arcul mic ab și arcul mare o să
mai Fie M un punct pe arcul mare
al cercului de exemplu punctul
m și vom nota arcul mare cu trei
litere a m b dacă ai extremitățile
unui arc de cerc sunt puncte diametral
opuse atunci arcul se numește semicerc
în acest desen a este un diametru
atunci arcul AB Se va numi semicerc
fie că este vorba despre arcul
portocaliu sau cel cu verde punctat
cele două semicercuri sunt egale
Deoarece ele reprezintă jumătăți
ale aceluiași cerc o să dăm în
continuare o definiție a interiorului
cercului Mulțimea punctelor din
plan situate la o distanță mai
mică decât R față de centrul cercului
formează interiorul cercului se
notează cu ind cerc de centru o
și rază r o ai este raza cercului
iar segmentul observăm că are lungimea
mai mică decât lungimea razei în
acest caz un spune că punctul p
este situat în interiorul cercului
și acum urmează definiția exteriorului
Mulțimea punctelor din plan situate
la o distanță mai mare decât R
asa de centrul cercului formează
exteriorul cercului se notează
cu X cerc de centru o și rază r
observăm că segmentul ochiul are
lungimea mai mare decât lungimea
razei o a în acest caz îmi spune
că punctul q este un punct situat
în exteriorul cercului există o
infinitate de astfel de puncte
situate în exteriorul cercului
și o ultimă definiție mulțimea
punctelor situate pe cerc reunită
cu interiorul cercului formează
discul de centru o și rază r discul
de centru o și rază r este format
din cercul de centru o și rază
r reunit cu interiorul acestuia
cu alte cuvinte un disc este un
cerc plin rețineți că cele mai
importante elemente ale unui cerc
sunt centrul și raza acestea definesc
cercul diametrul este cea mai mare
coardă și al este egal în lungime
cu dublul razei
Cercul- definiții și elementeAscunde teorie X
Navigare în lectii
Cumpara abonament
