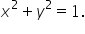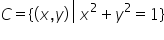Cercul trigonometric

cercul trigonometric este o noțiune

fundamentală a trigonometriei este

deosebit de important să înțelegeți

această noțiune pentru că ea face

posibilă înțelegere a trigonometriei

dar și a analizei matematice pe

care o vezi tu din anii următori

în cerc trigonometric este un cerc

având centrul în originea unui

sistem de axe x o y y iar raza

acestuia este egală cu unu din

acest motiv se mai numește și circ

unitate vom stabili și un sens

de construcție a unghiurilor În

cercul trigonometric semidreapta

o a se consideră fixă iar raza

mobilă om se poate deplasa în două

sensuri sensul pozitiv este sensul

invers acelor de ceasornic acesta

se mai numește și sens trigonometric

iar sensul negativ va fi sensul

orar punctul a se mai numește și

Punct inițial deoarece Orice unghi

se măsoară privind semidreapta

o a ca latură inițială a unghiului

cele două axe împart cercul trigonometric

în patru părți numite cadrane care

se numerotează astfel cadranul

1 cadranul 2 cadranul 3 și cadranul

4 coordonatele unui punct M situat

pe cerc vor fi definite astfel

abscisa este proiecția ortogonală

a razei om pe axa o x ordonata

este proiecția razei pe axa o y

Deci x este exista iar intreg ordonata

raza om se mai numește și raza

vectoare întrucât om poate fi privit

ca Vector de poziție a punctului

m Dacă aplicăm Pitagora În triunghiul

dreptunghic obm avem o b la pătrat

plus b m la pătrat egal cu om la

pătrat Deci x pătrat plus pătrat

egal cu 1 prin urmare coordonatele

tuturor punctelor situate pe cercul

trigonometric verifică relația

x la pătrat plus igrec la pătrat

egal cu 1 aceasta va fi și ecuația

cercului trigonometric Dacă punctul

m este situat în primul cadran

atunci abscisa și ordonata vor

fi pozitive Dacă M este situat

în cadranul 2 atunci AB și stai

este negativă iar ordonata pozitivă

Dacă M este situat în cadranul

3 atunci ambele coordonate sunt

negative iar dacă m este situat

în cadranul 4 atunci abscisa este

pozitivă iar ordonata negativă

este important de remarcat faptul

că abscisa și ordonata unui punct

Nu sunt doar niște simple coordonate

ele reprezintă valorile funcțiilor

trigonometrice sinus și cosinus

pentru unghiul respectiv Iată dacă

notăm unghiul a o m cu alfa atunci

în triunghiul b om avem sinus de

Alfa este raportul dintre cateta

opusă și ipotenuză de sigle cu

m b supra om și egal cu y supra

1 egal cu y cosinus de Alfa este

cateta alăturată supra ipotenuză

b c egal cu o b supra om și egal

cu x pe 1 adică x prin urmare abscisa

reprezintă cosinusul unghiului

iar ordonata este sinusul în continuare

vom prezenta cele mai importante

unghiuri ale cercului trigonometric

lume exprimat măsurile acestora

în grade și radiani și voi Scrie

coordonatele punctelor de pe cerc

corespunzătoare acestora unghiuri

aici avem unghiul cu măsura de

0 grade Aici avem 90 de grade 90

plus 90 este 180 de grade 180 plus

90 270 270 plus 90 este egal cu

360 de grade dacă ne uităm la acest

punct observăm că este situat la

mijlocul acestui arc prin urmare

măsura acestui unghi va fi 90 de

grade supra 2 adică 45 de grade

și acum pornim de la zero în sens

trigonometric și numaram din 45

în 45 avem 0 45 90 90 plus 45 este

135 135 plus 45 este 180 plus 45

este 225 plus 45 270 270 plus 45

este 315 iar 315 plus 45 de de

360 de grade acum observăm că aceste

două puncte împart acest arc acestor

de cerc în trei părți egale Iată

arcul Acesta are aceeași lungime

cu arcul acesta și cu arcul acesta

prin urmare măsura acestui unghi

va fi o treime din măsura unghiului

drept 90 de grade împărțit la 3

este 38 pornim de la zero în sens

trigonometric și numărăm din 30

in 30 avem 0 30 de grade 60 de

grade 60 plus 30 90 90 plus 30

120 120 plus 30 150 urmează 180

180 plus 30 210 plus 30 240 plus

30 270 apoi 300 330 și 360 am exprimat

în grade cele mai importante unghiuri

din cercul trigonometric și acum

haide se exprimă măsurile acestora

și în radiani la 0 grade avem 0

radiani la 90 de grade avem pi

supra 2 radiani am văzut acest

lucru în lecția trecută deci să

reținem că un sfert de cerc are

pi supra 2 radiani apoi la 180

de grade avem pi radiani adică

pi supra 2 ori 2 se simplifică

2 și ne rămâne pi pi plus pi supra

2 ne dă 3 pi supra 2 iar 3 pixuri

2 plus pi supra 2 este 4 pi pe

2 adică 2 pini jumătate din pi

supra 2 este pi supra 4 prin urmare

la 45 de grade le corespund pi

supra 4 radiani acum pornim de

la zero mergem în sens trigonometric

și adună MPI supra 4 radiani avem

zero pipe 4 2 pe 4 se simplifică

și ne pi pe 2 3 pi pe 4 4 pipe

4 se simplifică 4 și ne rămâne

pe 5 pe 4 șase piept patru se simplifică

șine de 3pi pe 2 7 pi pe 4 8 fii

pe 4 se simplifică cu 4 și ne rămâne

2pi aici avem o treime din supra

2 adică pi supra 6 și pornim e

are de la zero și adunăm pi pe

6 avem 0 pi pe 6 2 pi pe 6 adică

pipe 3 3 pi pe 6 adică pi supra

2 4 pipe 6 se simplifică șine de

2pi pe 3 5 pe 6 6 Pi pe 6 adică

pi 7 pi supra 6 8 pi supra 6 adică

4 pi pe 3 9 pi pe 6 adică 3 pipete

210 pipe 6 adică 5pi supra 3 11

pi pe 6 și 12 pi pe 6 adică 2 pi

am exprimat Așadar cele mai importante

unghiuri din cercul trigonometric

în grade și radiani și acum să

vedem Care sunt coordonatele acestor

puncte situate pe cerc aici avem

punctul de abscisă 1 și ordonată

0 aici avem punctul de coordonate

0 1 aici avem punctul de coordonate

minus 1 0 iar Aici punctul de coordonate

0 și minus 1 să vedem acum Care

sunt coordonatele acestor puncte

după cum spuneam mai devreme aici

ar trebui să scriem cosinusuri

și sinusul unghiului respectiv

prin urmare aici ar trebui să scriem

cozi de 30 sin de 30 cos de 45

sin de 45 colț de 60 sinus de 60

Iată metodă mai rapidă de a scrie

aceste valori avem fracția 1 pe

2 pe 2 3 pe 2 acum mergem invers

unu pe doi doi pe doi și trei pe

doi și acum punem radical la numărător

radical din 1 este 1 de cele stăm

așa avem radical din 2 radical

din 3 avem radical din 1 care este

1 apoi radical din 2 și radical

din 3 acestea sunt coordonatele

punctelor din primul cadran în

cadranul 2 avem aceleași coordonate

în modul însă abscisele sunt negative

punctul acesta este simetricul

acestui punct prin urmare vom împrumuta

aceste coordonate cu precizarea

că abscisa este negativă Deci avem

minus 1 pe 2 și radical din 3 pe

2 acest punct este simetricul acestuia

Așadar o să avem un minus radical

din 2 pe 2 și radical din 2 pe

2 apoi avem minus radical din 3

pe 2 și 1 pe 2 mergem în cadranul

între ei unde ambele coordonate

sunt negative acest punct este

simetricul punctului de mai sus

Așadar copiem aceste coordonate

și Ambele sunt negative avem minus

radical din 3 pe 2 și minus 1 pe

2 punctul acesta va fi simetricul

acestui punct așa dar mama mea

A minus radical din 2 pe 2 radical

și minus radical din 2 pe 2 apoi

minus 1 pe 2 minus radical din

3 pe 2 mergem la cadranul 4 Aici

abscisa este pozitivă iar ordonata

negativă acest punct este simetricul

acestei punct Așadar vom avea aceleași

coordonate în modul abscisa este

pozitivă Deci avem unul pe 2 Dar

ordonata negativă a minus radical

din 3 supra 2 Acum ne uităm aici

avem radical din 2 supra 2 și minus

radical din 2 supra 2 și aici avem

radical din 3 supra 2 și minus

1 pe 2 acestea sunt coordonatele

celor mai importante puncte situate

pe cercul trigonometric Și acum

dacă vă întreb Cât este cosinus

de 135 de grade ar trebui să știți

cosinus Haideți să scriem în radiani

cosinus de 3 pe 4 mergem de la

zero în sens trigonometric ne uităm

la unghiul de 3 pi pe 4 cosinus

este abscisa acestui punct Așadar

avem minus radical din 2 pe 2 dacă

vreau să calculez tangentă de cinci

pai pe patru palme exprimat tangenta

ca fi în raportul dintre sinus

și cosinus avem sinus de 5 pe 4

supra cosinus de 5 pe 4 o să vedem

în lecțiile următoare cât unguent

Ah se definește ca fiind raportul

dintre sinus și cosinus sinus de

5 pe 4 Iată aici avem cinci pe

patru sinusul este ordonata Deci

avem minus radical din 2 pe 2 supra

minus radical din 2 pe 2 se simplifică

și ne dă 1 să știți că putem avea

și unghiuri cu măsura mai mare

de 2pi Haide să calculăm de exemplu

sinus de 3pi pornim de la zero

în sens trigonometric avem 0 2

pi și 3 pi ne oprim aici Așadar

observăm că sinus de 3pi este egal

cu sinus de pi pentru că am ajuns

în același punct iar sinus de pi

va fi ordonat acestui punct adică

0 de asemenea putem avea și unghiuri

negative De exemplu dacă vreau

să calculez sinus de minus pi supra

6 dacă aș avea sinus de pi supra

6 ați pornit de la zero în sus

adică în sens trigonometric până

la pi supra 6 din moment ce avem

minus pi supra 6 înseamnă că trebuie

să plec în sens invers adică în

sens orar aceeași distanță Așa

da de la zero mergem în jos aceeași

distanță ca și aici și ajungem

la 11:00 pi supra 6 prin urmare

sinus de minus pi pe 6 este același

lucru cu sinus de 11 pi supra 6

iar sinus de 11 pi supra 6 este

minus 1 pe 2