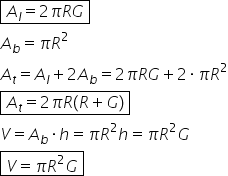Cilindrul circular drept (aplicații)

să aplicăm acum formulele pe care

le am votat pentru cilindru circular

drept și ni se dă această problemă

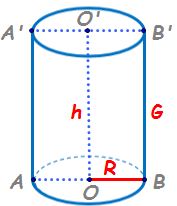
diametrul bazei unui cilindru circular

drept are lungimea de 16 cm și

aria laterală este de 240 cm pătrați

să găsim aria totală și volumul

cilindrului acum mi se spune că

diametrul bazei are lungimea de

16 cm prin urmare dacă notăm cu

R mare cum a notat și în formula

raza acestui cerc atunci noi știm

că raza cercului este egală cu

jumătate din lungimea diametrului

adică de pe 2 unde am notat cu

d chiar o să trec aici de este

diametrul cercului și avem 16 cm

DC egal mai departe cu 16 supra

2 adică centimetri și am găsit

Cât este raza acestui cerc mai

cunoaștem că aria laterală este

de 240 ori pe centimetri pătrați

și să găsim aria totală și volumul

cilindrului Care e formula ariei

totale ca să vedem de Ce elemente

avem nevoie aria totală are următoarea

formulă doi fii aer pe lângă G

adunat cu aer și formula pentru

volum este pi R pătrat înmulțit

cu asta înseamnă că avem nevoie

de rază de Jean de terminat raza

dar și de lungimea generatoarei

cum determinăm lungimea acestei

generatoare pâine folosind această

informație aria laterală are următoarea

formulă 2 pi R orice și știind

că este egal mai departe cu 240

pete Păi ce înseamnă asta rezultă

că avem următoarea egalitate 2

ori pe înmulțit cu r Care este

8 înmulțit mai departe cu lungimea

generatoarei G egal cu 240 ore

ep și acum Avem o ecuație putem

foarte simplu să îl determină pe

G vom împărți putem să împărțim

mai întâi la opt ore fi de exemplu

împărțim la 8 ore fii aici trebuie

să trecem în paranteză ca Să arătăm

că împărțim și la 8:00 dar și la

piept și ce vom obține IP împărțit

la pio să ne dea unul și mai avem

opt împărțit la 8 1 Deci aici ne

rămâne 2 ori 2 înmulțit cu g egal

cu fi împărțit la p este unul 240

împărțit la 8 dă 30-a și rezultă

că generatoarea are 15 cm și acum

ne întoarcem formule aria totală

este egală cu 2 ori fie înmulțit

cu rază 8 cm pe lângă generatoare

este 15 adunat cu 8 și vom avea

2 ori 816 trecem direct 16 ori

înmulțit cu 2316 ori 23 ne dă 368

Pi cm pătrați acum pentru volum

ori aer la a doua adică 8 la a

doua înmulțit cu 15 avem aici lungimea

generatoarei și avem 64 ori 15

un multe cupe vom obține 960p centimetri

cubi și astfel am de terminat și

aria totală și volumul acestui

cilindru circular drept o altă

problemă între un cilindru circular

drept se știe că Diagonala secțiunii

axiale este de 8 cm și face cu

planul bazei un unghi cu măsura

de 60 de grade Să găsim aria laterală

aria totală și volumul cilindrului

într un cilindru circular drept

Ce înțelegem prin secțiune axială

secțiunea axială e reprezentată

de fapt de un dreptunghi și anume

acest drept un pe care chiar putem

să îl notăm a b c d Lățimea dreptunghiului

este dată de diametrul cercului

de la bază iar lungimea este cât

generatoarea cilindrului acum noi

știm că diagonala aceste secțiunii

axiale este de 8 cm atunci să construim

diagonala de exemplu diagonala

AC avem de ales între a c și d

b știind că este de 8 cm și mai

știm că ai a face cu planul bazei

un unghi cu măsura de 60 de grade

Deci ei ce face cu planul bazei

un unghi cu măsura de 60 de grade

Panda Care este acest unghi Păi

cum ce b este perpendiculară pe

planul bazei înseamnă că proiecția

punctului C pe acest plan este

punctul b punctul A este în plan

Deci proiecția lui Pe plan este

chiar punctul însuși asta înseamnă

că vorbim de unchiul făcut de dreptele

ac și ab adică de acest unghi avem

aici 60 de grade Să notăm măsura

unghiului c AB este de 60 de grade

Trebuie să găsim aria laterală

aria totală și volumul acum ca

să găsim aria laterală vom avea

nevoie și de generatoare dar și

de raza acestui cerc și atunci

Haideți să mutăm aici cu R mare

raza cercului și să vedem cum putem

să găsim generatoarea trec aici

g și raza Păi ce fel de triunghi

este triunghiul c b a este un triunghi

dreptunghic pentru că c b este

perpendiculară pe planul bazei

a b este inclusă în planul bazei

este înseamnă că c b este perpendiculară

și pe a b deci putem să trecem

că avem aici un unghi de 90 de

grade un să notăm că măsura unghiului

c b a este de 90 de grade cu alte

cuvinte avem aici un triunghi dreptunghic

deci putem să aplicăm funcții manometri

c pentru că știm măsura acestui

unghi și cunoaștem și lungimea

ipotenuzei AC ce se aplică mai

întâi mie ca să determinăm generatoarea

putem să aplicăm funcția sinus

pentru că generatoarea se opune

acestui unghi sinus de unghiul

A este egal cu raportul dintre

lungimea catetei opuse unghiului

adică si b supra lungimea ipotenuzei

adică ace și acum vom înlocui avem

sinus de 60 de grade egal cu c

b reprezintă generatoarea cilindrului

Deci trecem g mare de la generatoare

AC este 8 cm Cât este sinus de

60 de grade avem aici e radical

din 3 supra 2 egal cu Z supra 8

de unde rezultă că G egal cu 8

radical din 3 pe 2 adică 4 radical

din 3 cm și putem să notăm aici

că avem patru radical din trei

și aceasta este generatoare a cilindrului

circular drept un să găsim acum

și raza ca să găsim raza Ce determină

mai întâi determinăm diametrul

a b și atunci putem să aplicăm

aici funcția cosinus sau putem

să aplicăm teorema lui Pitagora

În triunghiul a b c pentru că știm

și această catetă și ipotenuza

o să aplicăm cosinus cosinus de

60 de grade sau mai întâi cosinus

de unghiul a egal cu lungimea catetei

alăturate unghiului adică ab supra

ipotenuză lungimea ipotenuzei adică

a c și avem acum cosinus de 60

de grade egal cu a b supra AC este

8 de unde rezultă că cosinus de

60 de grade ne dă 1 supra 2 egal

cu ab supra 8 rezultă că a b ne

de 4 cm figure aici aveam un unghi

de 30 de grade acesta și puteam

să aplicăm În triunghiul c b a

care un triunghi dreptunghic puteam

să aplică teoremă unghiului de

30 de grade și rezultat că ab are

întradevăr jumătate din lungimea

segmentului ac Deci 4 cm bun am

găsit că a b are 4 cm de unde rezultă

că raza Care este egală cu ab supra

doi ne va da patru supra 2 adică

doi centimetri și atunci să ștergem

aici trecem ca avem 2 cm cu toate

aceste date putem să ștergem aici

și vom calcula mai întâi aria laterală

trece în formula este egală cu

2 pi r g și atunci rezultă că aria

laterală cu cât este egal avem

2 înmulțit cu pin mulți tcu raza

Care este de 2 cm de ciori 2 înmulțit

cu generatoarea are 4 radical din

3 centimetri și Avem așa 2 ori

2 4 x 4 16 pi înmulțit cu radical

din 3 centimetri pătrați să găsim

acum și aria totală formula este

2 pi R pe lângă G Plus R de unde

rezultă că aria totală Cu cât este

egală Avem doi ori fie înmulțit

cu r Care este 2 cm înmulțit cu

paranteză G Plus aer adică Patrula

de cal din 3 adunat cu 2 aici nu

putem să facem suma însă putem

să desfacem paranteza Înmulțind

pe doi ori doi patru pai Deci înmulțim

pe 4pi cu fiecare termen din paranteză

în parte și Avem așa patru ori

patru Nevada 16 radical din 3 adunat

cu avem patru pai ori doi adică

8 pi și putem să trecem aici în

paranteză să notăm centimetri pătrați

în final să găsim volumul acestui

cilindru formula este pătrat orice

Deci rezultă că volumul este egal

cu pi înmulțit cu rază la a doua

adică 2 la a doua înmulțit cu 4

radical din 3 și avem așa 4 x 4

16 pi ori radical din 3 centimetri

cupe iată că valoarea volumului

este egală cu valoarea ariei laterale

însă atenția aici avem aria laterală

deci vorbim de 16 pi radical din

3 centimetri pătrați și aici avem

centimetri cubi