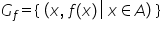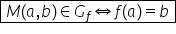Citirea graficului unei funcții

vreau Cum să rezolvăm două aplicații

în care vom citi graficele a două

funcții și avem aici prima întrebare

mulțimea punctelor reprezentate

în sistemul de axe poate fi graficul

unei funcții Iată avem aici unu

doi trei puncte acestea cu portocaliu

aceste trei puncte pot fi reprezentarea

geometrică a graficului unei funcții

pe Haide să trecem mai întâi coordonatele

acestor puncte primul punct are

abscisa 1 ordonată minus 1 este

Trecem unu și minus unu acest punct

are abscisă 2 iar ordonata este

1 Iar acest punct are abscisă 2

iar ordonata este 3 bun Acum avem

și coordonatele Ce ziceți aceste

trei puncte pot fi reprezentarea

geometrică a graficului unei funcții

vă las puțin timp să vă gândiți

Păi dacă nu va dat deja seama atunci

Haideți să facem și un tabel de

Valori și ce vom trece în acest

tabel pe prima linie tăcem valorile

absciselor iar pe a doua linie

Dacă am avea o funcție Atunci trebuie

să trecem valorile funcției în

accizele respective dacă pe funcția

argerich mof aici ar trebui să

trecem f de x însă loc de fb x

vom scrie y pentru că pe axa o

y trecem valorile funcției ca să

nu ne încărcăm foarte mult cu notații

Haide să trecem direct y7 prima

linie trecem valorile absciselor

pe acest punct are abscisă 1D și

trecem unul care este ordonata

minus unu ștergem aici minus unu

acest punct are abscisa 2 și ordonata

1 Deci trecem 2:01 acest punct

are abscisa A2 Da și ordona la

3:00 bun dar pe 2 abscisa 2 Deja

e trecută în atunci Haideți să

facem așa trecem aici unu și al

treilea punct are abscisa ordonata

A3 multe uitând un la acesta poate

fi acesta tabelul de Valori al

unei funcții nu de ce nu pentru

că dacă ar fi funcție atunci fiecare

element din prima mulțime trebuie

să aibă un singur corespondent

în cea de a doua mulțime și atât

că numărul 2 are doi corespondențe

și pe 1 și pe 3 Tec răspunsul este

nu mulțimea formată de aceste trei

puncte nu poate fi graficul unei

funcții pentru că aici Iată avem

abscisa punctul de abscisă 2 pare

ordonate lemn și 1 și 3 cu alte

cuvinte în această situație când

aveți cel puțin două puncte care

au aceeași abscisă și ordonate

diferite atunci graficul respectiv

nu este graficul unei funcții următoarea

aplicație avem aici o funcție definită

pe d cu valori în ce acesta e domeniul

de definiție acesta este codomeniul

iar în acest sistem de axe x o

y avem reprezentarea geometrică

a graficului funcției f prin aceste

patru puncte avem aici un punct

al doilea al treilea și al patrulea

și acum Haideți să răspundem la

câteva întrebări prima întrebare

Cât este f de minus 1 și cât este

f de 2 adică valorile funcției

în punctul de abscisă a minus unu

și în punctul de abscisă 2 Eu zic

că cel mai bine ar fi să facem

tabelul de Valori pentru funcția

f și avem aici Haideți să notăm

trasăm tabelul și vom avea x și

valorile funcției ceva trecem pentru

abscisă pentru variabila x acest

punct are abscisa minus unu Deci

dăm lui x valoarea minus 1 și aici

trebuie să avem e f de minus unu

Cât este f de minus 1 pe acest

punct are ordonata 1 asta înseamnă

că unul este f de minus unu și

am și răspuns la prima întrebare

ce mai avem următorul punct are

abscisa 1 Deci trecem 1 iar ordonata

adică e f d 1 este egală cu 4 m

mai departe al treilea punct are

abscisă 2 ordonata adică f de 2

ne dă 3 și ultimul punct are abscisă

3 trecem aici 3 iar ordonata este

1 adică FD 3 ne dă 1 bun Păi de

ce să notăm ce am obținut f de

minus 1 este egal cu 1 ștergem

semnele de întrebare f de minus

unu spus că ne dă 1 f de 2 Păi

dacă x este 2 f de 2 este 3 ce

am răspuns la cerința amic acum

să vedem care este domeniul de

definiție al funcției deja am trecut

aici domeniul de definiție este

reprezentat de mulțimea formată

din aceste elemente Haideți să

notăm d este egal cu avem elementele

minus unu unu doi și trei de adevăr

putem să și verificăm că este o

funcție Iată fiecărui element din

această mulțime corespunde câte

un singur element în a doua mulțime

să vedem acum care este imaginea

funcției f o imaginea funcției

f e reprezentată de valorile pe

care le ia concret funcția f adică

aceste numere și avem mn este formată

din elementele 1 4 3 și 1 dar pe

unul deja la întrecut Deci aceasta

este imaginea funcției f mulțimea

formată din elementele 1 4 și 3

altă întrebare să vedem dacă această

mulțime cu elementele 1 2 și 3

poate fi codomeniul funcției f

Păi ce trebuie să se întâmple întotdeauna

ce relație avem între imaginea

unei funcții și codomeniul e bine

întotdeauna imaginea funcției Haideți

să mutăm aici trebuie să fie inclusă

în codomeniu Păi avem această relație

Haideți să vedem mulțimea formată

din elementele 1 4 și 3 este Cumva

inclusă în această mulțime formată

din elementele 1 2 și 3 nu este

inclusă deci putem să dăm aici

această idee să notăm cu roșu tăiem

aici pentru că nu avem incluziunea

asta înseamnă că mnd e nu este

inclusă în mulțimea C cu alte cuvinte

această mulțime nu poate fi codomeniul

funcției este răspunsul la întrebare

este nu pentru că nu avem această

relație de incluziune ultima întrebare

Haide să se vadă păstrăm tabelul

să vedem dacă punctul de coordonate

3 și 2 aparține graficului funcției

f apoi putem să verificăm acest

lucru uităm dune în tabelul de

Valori dacă abcisa este 3 ordonata

este 2 iar dacă acciza este 3 ordonata

este 1 deci de fapt acest punct

d coordonate 3 și 2 nu aparține

graficului funcției Deci răspunsul

este și aici și să ne amintim că

întotdeauna un punct care aparține

graficului funcției trebuie să

aibă această formă o nota aici

x și fdx doar un asemenea punct

aparține graficului funcției f

acum dacă îi dăm lui x valoarea

3 atunci punctul de coordonate

3 si F de 3 aparține graficului

funcției f însă acest punct Cu

cât este egal echivalent cu trei

și F de 3 este 1 Da deci punctul

de coordonate 3 și 1 aparține graficului

funcției f nu punctul de coordonate

3 și 2 și cu aceasta sa încheiat

exercițiul nostru și iată că folosind

una de citirea reprezentării geometrice

a graficului funcției am putut

să determinăm și domeniul de definiție

al iei și imaginea funcției precum

și o să găsim răspunsul la aceste

două întrebări