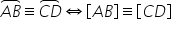Coarde şi arce în cerc (teorie)

în această lecție o să vedem câteva

teoreme referitoare la coardă și

arce în cerc prima teoremă în același

cerc sau în cercuri congruente

la arce congruente corespund cu

ardei congruente mai putem spune

că arcele congruente sunt sub întinse

de fard de congruente în această

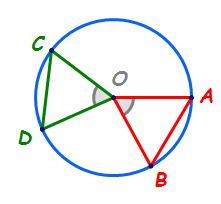
figură arcul AB este congruent

cu arcul cd și trebuie să arătăm

că segmentele AB și CD sunt congruente

pornind de la relația scrisă în

ipoteză și anume arcul AB este

congruent cu arcul CD asta înseamnă

că măsurile celor două arce sunt

egale măsura arcului AB este egală

cu măsura arcului CD dar măsura

arcului AB este egală cu măsura

unghiului la centru a o b iar măsura

arcului CD este egală cu măsura

unghiului la centru corespunzător

și atunci din această relație Putem

să scriem că măsura unghiului aob

este egală cu măsura unghiului

c o d din această relație va rezulta

că Unghiul aob va fie congruent

cu unghiul c o d în continuare

vom arăta că Triunghiurile a o

b și c o d sunt congruente știind

că o a și o c sunt raze Așadar

cele două segmente vor fi congruente

o A este congruent cu oc pentru

că sunt raze apoi am arătat că

unghiul a o b este congruent cu

unghiul c o d iar segmentele o

b și o d sunt congruente pentru

că și acestea sunt raze o b este

congruent cu o d fiind raze din

cele trei relații va rezulta că

triunghiul a o b este congruent

cu triunghiul c o d conform cazului

de congruență latura unghi latura

iar congruență acestor două triunghiuri

implică și congruența segmentelor

AB și CD A ba fie congruent cu

cd și am demonstrat astfel că arcele

congruente sunt sub întinse de

cu ardei congruente este valabilă

și reciproca aceste teoreme în

același cerc sau în cercuri congruente

la coardă congruente corespund

arce congruente și atunci Putem

să scriem această relație segmentul

a b este congruent cu segmentul

CD Dacă și numai dacă arcul AB

este congruent cu arcul CD urmează

teorema numărul 3 într un cerc

diametru perpendicular pe o coardă

trece prin mijlocul coardei și

prin mijlocul arcelor subîntinde

de coardă În figura de mai jos

avem o coardă AB și diametrul mn

perpendicular pe această coardă

trebuie să arătăm că diametrul

MN trece prin mijlocul coardei

a b prin mijlocul arcului mic ab

și prin mijlocul arcului mare ab

am demonstrat ceastă teoremă Se

știe că mn este diametru mn este

perpendicular pe AB și am notat

cu p intersecția dintre dreptele

MN și ab trebuie să arătăm că punctul

p este mijlocul segmentului AB

cu alte cuvinte arătăm că Segmentul

ab este congruent cu segmentul

pe b apoi trebuie să arătăm că

arcul a n este congruent cu arcul

n b și că arcul a m este congruent

cu arcul MB dacă o a și o b sunt

raze înseamnă că aceste două segmente

au aceeași lungime adică triunghiul

AOB este un triunghi isoscel Dacă

dreapta a este perpendiculară pe

AB înseamnă că o este înălțime

Dar într un triunghi isoscel înălțimea

este și mediană mediatoare și bisectoare

dacă o este mediană atunci punctul

p este mijlocul segmentului AB

și astfel am demonstrat prima relație

din concluzia teoremei știind că

o a este egal cu OB pentru că sunt

raze și atunci rezultă că triunghiul

AOB este un triunghi isoscel Opa

este înălțime pentru că ab este

perpendiculară pe AB și atunci

va rezulta că o p este și mediană

Deci punctul P va fi mijlocul segmentului

AB prin urmare Segmentul ab este

congruent cu segmentul pe b am

demonstrat prima relație Acum trebuie

să arătăm că arcul a n este congruent

cu arcul n b în acest triunghi

isoscel o pe va fi și bisectoarea

unghiului aob rezultă că unghiul

aoc va fi congruent cu unghiul

b o p prin urmare unghiuri a o

n va fi congruent cu unghiul b

o n Dacă aceste două unghiuri sunt

congruente rezultă că arcul a n

va fi congruent cu arcul MB pentru

că măsura unui arc este egală cu

măsura unghiului la centru corespunzător

din această relație va rezulta

arcul a n este congruent cu arcul

and b am demonstrat astfel și cea

de a doua relație din concluzia

teoremei Ultima relație se demonstrează

asemănător nu o să mai fac și această

demonstrație de țineți așa dar

că întru un cerc diametru perpendicular

pe o coardă trece prin mijlocul

coardei și prin mijlocul arcelor

subîntinde de acea coardă continuăm

cu teorema numărul 4 două coardei

ale unui cerc sunt congruente Dacă

și numai dacă sunt egal depărtate

de centru Segmentul ab este congruent

cu segmentul CD dacă și numai dacă

distanța de la punctul o la AB

este egală cu distanța de la punctul

o la CD Maria amintesc că distanța

de la un punct la o dreaptă este

perpendiculară dusă din acel punct

pe dreaptă această teoremă are

o dublă implicație prin urmare

trebuie să facem două demonstrații

o să începem cu demonstrația implicații

directe pornind de la relația ab

congruent cu cd trebuie să demonstrăm

că distanța de la punctul o la

dreapta AB este egală cu distanța

de la punctul o la dreapta CD mai

exact trebuie să demonstrăm că

segmentele o m și o n sunt congruente

având în vedere că o a și o b sunt

raze le vor fii congruentei și

atunci Putem să scriem că triunghiul

AOB este isoscel om este perpendiculară

pe AB din construcție înseamnă

că o m este înălțime dar între

un triunghi isoscel înălțimea este

și mediană înseamnă că punctul

m este mijlocul laturii AB și atunci

Putem să scriem că lungimea segmentului

a m este jumătate din lungimea

segmentului AB în mod Analog se

arată că triunghiul c o d este

isoscel pentru că o c și o d sunt

raze o n este perpendiculară pe

CD înseamnă că o m este înălțime

prin urmare o n va fi mediană Deci

punctul n va fi mijlocul laturii

CD și Putem să scriem că lungimea

segmentului CN este jumătate din

lungimea segmentului c d de la

ce este două segmente ab și cd

sunt egale ele au aceeași lungime

Știind acest lucru din ipoteză

a b este egal cu cd și atunci din

aceste trei relații din relațiile

1 2 și 3 va rezulta că a m este

congruent cu CN în continuare o

Să arătăm că triunghiul a o m este

congruent cu triunghiul c o n acestea

sunt triunghiuri dreptunghice și

atunci este suficient să scriem

două elemente corespondente congruente

am găsit că a m este congruent

cu CN și mai știm că AO este congruent

cu oc acesteia fiind Raise și atunci

va rezulta că cele două triunghiuri

sunt congruente conform cazului

de congruență ipotenuză catetă

mai știm că a o este congruent

cu o c Acestea fiind raze și atunci

din aceste două relații va rezulta

conform cazului de congruență ipotenuză

catetă că triunghiul a o m este

congruent cu triunghiul c o n iar

congruență acestor două triunghiuri

implică și congruența segmentelor

o m și o n dar o m și o n erau

distanțele de la punctul o la cele

două cu ardei și atunci Putem să

scriem că distanța de la punctul

o la dreapta AB este egală cu distanța

de la punctul o la dreapta CD am

demonstrat implicația directă a

aceste litere m mai trebuie să

demonstrăm și implicația inversă

o să șterg prima demonstrație pentru

a avea spațiu pentru a demonstra

implicația inversă pornim de la

faptul că distanța de la punctul

o la AB este egală cu distanța

de la punctul o la cd și trebuie

să arătăm că segmentul ab este

congruent cu segmentul CD Unde

mostra mai întâi congruență a triunghiurilor

hașurate a o m și c o n de data

aceasta știind că o m este congruent

cu o n Acest lucru se dă în ipoteză

mai știm că o a este congruent

cu oc pentru că sunt raze și atunci

va rezulta conform cazului de congruență

ipotenuză catetă că triunghiul

a o m este congruent cu triunghiul

c o n din relația aceasta va rezulta

că a m este congruent cu CN în

mod asemănător se arată că Triunghiurile

a o b m și o d n sunt congruente

Analog arătăm că triunghiul o b

m este congruent cu triunghiul

o d n ia din congruența celor două

triunghiuri va rezulta că segmentul

b m este congruent cu segmentul

d n am arătat astfel că lungimea

segmentului a m este egală cu lungimea

segmentului CN și că lungimea segmentului

b m este egală cu lungimea segmentului

dm adunăm la aceste două relații

membru cu membru și obținem că

a m plus b m este egal cu c n plus

d n m m p formează lungimea segmentului

AB iar c n plus n d formează lungimea

segmentului CD am arătat astfel

că cele două coardei au aceeași

lungime deci putem să scriem că

Segmentul ab este congruent cu

segmentul cd și astfel am demonstrat

și implicația inversă urmează teorema

numărul 5 ultima teoremă Dacă două

coardei ale unui cerc sunt paralele

atunci arcele cuprinse între ele

sunt congruente Dacă AB este paralel

cu cd atunci arcul AC va fi congruent

cu arcul BD