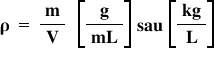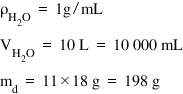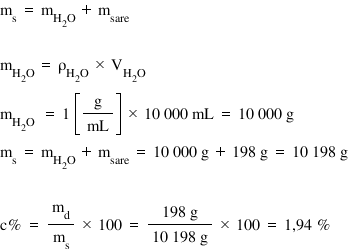Concentraţia procentuală - aplicaţii
Partajeaza in Google Classroom
Transcript
lecția trecută am discutat despre
concentrația procentuală și despre
concentrația molară a soluțiilor
concentrația procentuală reprezintă
masa de soluție care o notăm cu
m d și eu am în grame dizolvată
în 100 de g de soluție valoarea
concentrației procentuale este
dată de relația m b supra ms-101
MS reprezintă masa soluției iar
concentrația molară reprezintă
numărul de moli de substanță dizolvată
între un litru de soluție formula
pe care aduce o dată trecută prin
regula de trei simpla este aceasta
concentrația molară este egală
cu numărul de moli de soluții volumul
de soluție în lecția aceasta vom
face câteva exemple de calcul pentru
a vedea cum putem utiliza în probleme
relațiile de calcul ale centrale
cu toții știm că apa mării este
sărată deoarece conține peste 60
de soluții printre care și clorura
de sodiu Haideți să vedem care
este de fapt concentrația procentuală
de clorură de sodiu din apa mării
știind că între un kilogram de
apă sărată sunt 27 de g de sare
kilogramul de apă sărată reprezintă
masa soluției adică mes care transformat
în grame este egal cu 1.000 de
g m d e reprezintă masa solutul
urii adică masa de sare astfel
Aplicând formula concentrației
procentuale MD supra MS ori 100
și înlocuind cu valorile pe care
le cunoaștem și anume 27 de g supra
1.000 de g 100 obținem o concentrație
procentuală de 2 Deci pare o concentrație
destul de mică dar este suficient
să simțim gustul Sărat al apei
de mare am zis data trecută că
mai putem calcula concentrația
procentuală și Folosind regula
de trei simpla definiția concentrației
procentuale spunea că aceasta Reprezintă
cantitatea de solutie care se găsește
în 100 de g de soluție iar în problema
noastră noi știm că avem 27 de
g de clorură de sodiu în 1.000
de g de soluție 27 de g 100 de
g este egal cu x grame ori 1.000
de g ceas felul x care reprezintă
o valoare concentrației procentuale
este egal cu 27 ori 100 supra 1000
Deci obținem că valoarea concentrației
procentuale este 2 si acum o să
vorbim puțin despre un alt fel
de apă sărată Băi astăzi vreodată
murături Sau măcar vă te ajuta
părinții toamna când se pregătesc
murăturile dacă Da Atunci știți
că se folosește saramura pentru
a conserva cât mai bine castraveți
sau gogonelele Eu vreau nu vreau
trebuie să o ajut pe mama în fiecare
toamnă cu murăturile în ceea ce
privește saramura mama are o regulă
pentru fiecare litru de apă câte
o lingură de sare și încă puțin
încă puțin mai se pare prea bag
așa că la 10l de apă Pun întotdeauna
18 linguri de sare dacă o lingură
de sare înseamnă 18 g de sare Haideți
să calculăm concentrația procentuală
a sării din saramură pentru astfel
de calcule trebuie să cunoaștem
densitatea solventului să ne reamintim
că densitatea se notează cu litera
grecească ro și reprezintă masa
unității de volum adică câte kilograme
cântărește 1 L de soluție sau Câte
grame cântărește un miel de solurile
densităților diferitelor substanțe
sunt tablete deci nu trebuie să
le știm de pe de rost în cazul
acesta fiind vorba de apă densitatea
este de un gram pe mililitru adică
un mililitru de apă cântărește
un gras ăsta există multe fluide
cu densitate mai mică sau mai mare
decât 1 gândiți Voi numai puțin
la mierea si asta are o densitate
de 1 g pe mililitru motiv pentru
care 1 l de miere Spre exemplu
este cu mult mai greu decât 1 l
de apă acum că am lămurit Care
e treaba cu densitatea putem calcula
greutatea în grame a masei soluție
Deci masa de apă este egală cu
densitatea apei ori volumul la
adică masa de apă este egală cu
1 g pe mililitru ori volumul de
apă care este după cum am spus
10 L și transformat în mililitri
Deci 10 ori 1000 înseamnă că este
egal cu 10.000 de mililitri se
obține masa solventului adică masa
de apă care este egală cu 10.000
de g după cum am spus și lecția
trecută masa de soluție este egală
cu masa de solvent plus masa de
soluție Deci în cazul nostru este
egală cu masa de apă plus masa
de sare Ce este egal cu 10.000
de g plus 11 ori 18 g a spus că
folosim 18 linguri de sare și în
fiecare lingură sunt câte 18 g
de sare Deci avem un total de 10198
grame de soluție Observați că pentru
a obține valoarea masei de soluție
a am adunat glume cu grame la fel
pentru a obține evaluarea corectă
a concentrației procentuale și
masă salutului MD și masa soluției
m trebuie să fie exprimate în aceeași
unitate de măsură Deci nu vom folosi
în calcule valori exprimat în grame
mulți tei sau împărțite la Matei
în kilogram Așadar concentrația
procentuală este MD supra MS ori
100 și înlocuind cu valorile în
grame pe care le am obținut mai
devreme rezultă că valoarea concentrației
este egală cu 198 de g de soluție
a 10.000 198 grame de soluție ori
100 și este egală cu 1 la sută să
vedem acum Ce cantitate de clorură
de sodiu în ar trebui pentru a
obține 200 g de soluție de clorură
de sodiu 10% și de asemenea De
ce volum de apă e nevoie pentru
astfel de soluție Deci masa soluției
este egală cu 200 de g concentrația
este 10% iar masa de solutie este
valoarea necunoscută pe care trebuie
să o aflăm la fel și volumul de
apă e o valoare necunoscută pentru
a calcula masa de soluție formula
concentrației procentuale MD supra
MS ori 100 de unde rezultă că masa
de soluție gală cu valoarea concentrației
procentuale oems supra 100 și înlocuind
cu valorile pe care le avem din
problema MB este egal în continuare
cu 10 ori 200 de g supra 100 și
obținem că masa de solutie este
de 20 de g pentru a calcula volumul
de apă trebuie mai întâi să calculăm
masa de apă știind că masa de soluție
este egală cu așa de solvenți Adică
acum asta de apă plus masa de solutie
Dică cu m d rezultă că masa de
apă este egală cu 200 minus 20
Deci cu 180 de grade și am discutat
mai înainte despre faptul că densitatea
este egală cu masa asupra volum
astfel obține relația de calcul
pentru volumul apei și anume volumul
apei este egal cu masa de apă supra
densitatea apei știind că densitatea
apei este un gram pe mililitru
iar din cele două relații rezultă
că volumul de apă este egal cu
180 de g supra 1 g pe mililitru
Deci volumul de apă este egal cu
180 ML Deci vedem că pentru a obține
200 g de soluție de clorură de
sodiu trebuie să dizolvăm 20 de
g de sare în 180 ml de apă însă
în practică pentru exprimarea cantității
de soluție chimiștii preferă să
utilizeze concentrația molară de
aceea în partea a doua a acestei
lecții vom face și câteva aplicații
de calcul pentru concentrația molară
Teorie - Concentrația procentuală – aplicațiiAscunde teorie X
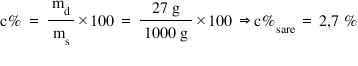
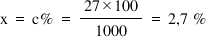
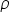, și reprezintă masa unității de volum (câte kg cântărește un L de soluție, sau câte grame cântărește un mL de soluție): 
Navigare în lectii
Cumpara abonament
