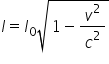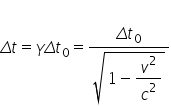Contracţia lungimilor. Dilatarea duratelor.

în cea de a patra Lecție despre

teoria relativității restrânse

am discutat despre cinematica relativă

stă adică vom folosi transformările

lorentz pe care le am am introdus

în lecția trecută fără ale derivă

afara dau demonstrație pentru a

vedea care sunt implicațiile acestor

transformări asupra cinematicii

sau mișcării unui corp cu viteze

comparabile cu viteza luminii în

vid întâi vom discuta despre așa

numită a contracția lungimilor

folosim aceeași aceleași două sisteme

de referință asprime și s referință

sistemul de referință inerțială

în care s este considerat în repaus

și exprim într o deplasare cu viteza

V de a lungul axei comunei x în

raport cu sistemul is Considerăm

o bară reprezentată prin acest

segment îngroșat plasată pe axele

comune Oysho exprime care are lungimea

l egală cu x 2 minus x 1 diferența

dintre coordonatele capetelor barei

în sistemul s și el Prime prin

definiție egală cu x x doi Prime

minus x 1 prim în de mult spre

Considerăm că măsurătoarea sau

măsurarea coordonatelor acestor

coordonate se face simultan în

fiecare din cele două sisteme de

referință inerțială și în concluzie

de el tot a și Delta te prind vor

fi egal cu zero în fiecare sistem

de referință atunci putem scrie

relația dintre el prim și el folosind

transformările lor mai exact al

prim este care este egal prin definiție

cu X prin 2 minus x prin 1 și prin

relația de transformare Lawrence

a cordonate x va fi egal cu gama

x 2 minus vt minus gama X1 minus

z t 1 și 2 si va fi egal cu gama

înmulțit cu el grupând termenii

Deci avem gama x 2 minus x 1 care

este egal cu el prin definiție

minus gama ori ori scuzați de 2

minute 1 care este prin definiție

de el tate în sistemul de referință

s Dar acest Delta t este egal cu

0 din nou pur și simplu pentru

că măsurăm coordonatele x 2 și

x 1 simultan și atunci obținem

că el prim este egal cu gama el

deja la acest moment se poate observa

o dependență de sistemul de referință

a lungimii unui a unei bare în

cazul acesta Pentru că el prim

nu este egal cu el pentru a scrie

mai explicită aceste această dependență

sistemul de referință să mai facem

un pas și anume să introducem așa

numitul sistem de referință propriu

al al unui eveniment sau al unui

sistem fizic este sistemul de referință

în care acel sistem fizic bara

în cazul nostru este în repaus

sau altfel spus este sistemul de

referință atașat legat de sistemul

fizic și deci în care el are viteză

0 în acest sistem de referință

toți parametrii capăt acest nume

propriu Deci însemn în sistemul

de referință propriu sau față de

sistemul de referință propriu lungimea

se va numi lungime proprie durata

unui eveniment sau unui proces

se numește durată proprie se notează

cu Delta t 0 și așa mai departe

Deci în general Când folosim acestor

index inferior 0 ne referim la

parametrul respectiv față sau măsurat

în sistemul de referință propriu

al sistemului fizic Deci în cazul

nostru putem scrie că el este egal

cu el 0 înmulțit cu radical din

1 minute pătrat pe ce pătrat pentru

că el prim Este în cazul nostru

în cazul probleme pe care nu am

pus o noi vara se află în repaus

față de sistemul prin deces prin

devine sistemul de referință propriu

al barei considerate și De ce îl

prim este egal cu el 0 în cazul

nostru și deci el lungimea în sistemul

de referință va fi l0 mulți cu

radical din 1 minute pătrat pe

ce pătrat dar vei este întotdeauna

mai mic decât ce am spus că viteza

luminii în vid este viteza maximă

pe care un sistem o poate avea

în fizică și Deci vei este mai

mic decât c De unde rezultă că

vei pătrat pe Ce pătrate mai mic

decât 1 Și de ce acest factor este

mai mic decât 1 și rezultă că dimensiunile

unui sistem fizic apar maxim în

sistemul de referință propriu Deci

indiferent ce alt sistem de referință

Considerăm lungimea măsurată în

acel sistem de referință el va

fi întotdeauna mai mică decât lungimea

măsurată în sistemul de referință

propriu l0 Am subliniat apar pentru

că Bineînțeles nu trebuie să înțelegem

prin contracția lungimilor o contracție

efectivă a sistemului fizic dacă

vă gândiți la exemplul pe care

îl am dat bara este aceeași Deci

avem aceeași bară măsurată de doi

observatori diferiți care obțin

lungimi diferite ale barei halprin

și el sau el și el zero Evident

asta nu înseamnă că bara acest

sistem fara poate avea două lungimi

diferite Dacă lungimile sunt diferite

ele sunt ca urmare a procesului

de măsurare mai exact contracția

lungimilor precum și alte efecte

relativiste pe care le vom vedea

imediat implică variația diferiților

parametri ale unui sistem fizic

datorită procesului de măsurare

nu modificarea lor efectivă un

alt comentariu foarte important

este următorul din această ecuație

vede imediat că Delta x prim este

egal cu Gamma Delta xc5 implică

o relativitatea spațiului măsurăm

lungimea barei și ne obținem rezultate

diferite în două sisteme de referință

inertiale diferite de Spațiul este

relativ în teoria relativității

restrânse de asemeni în lecția

trecută când am discutat despre

simultaneitate am văzut că dacă

considerăm un proces care are loc

fără o variație temporală fără

un interval temporal în sistemul

de referință obținem o unitar Vil

temporal egal cu minus gama V PC

pătrat Delta x în sistemul de referință

xprimm care este diferit de 0 Deci

și timpul este relativ în teoria

relativității restrânse El este

zero un sistem de referință și

diferit de 0 în ritm de referință

dacă vă aduceți aminte în prima

lecție de teoria relativității

restrânse am început prin discutarea

principiilor de bază ale spațiului

și timpului în mecanica clasică

și acolo era absolut timpul era

și el absoluți și aceste două noțiuni

erau complet independente de spațiu

și de timp în teoria relativității

restrânse spațiul e relativ timpul

e relativ și după cum am vorbit

ele nu mai sunt independente vorbim

de o o m un concept o noțiune comună

de spațiu timp care spațiu timp

de vine 9-a mărime absolută mai

exact se introduce aceasta acest

parametru Delta s ca fiind poziția

relativă Delta x pătrat plus Delta

pe topless Delta de pătrat acesta

este Delta l pătrat minus c pătrat

ori Delta t pătrat și luăm radicalul

A această distanță în spațiul 4

dimensionali spații timp devine

noua mărime invariabilă la transformările

de la un sistem de referință la

altul Deci dacă aplicăm acestui

de alta s transformările lorentz

observăm că Delta exprimi este

egal cu Delta l Deci spațiu timpul

aceasta aceasta sistem de coordonate

4 dimensionali devine 9 9 a mărimea

in variantă sau invariabilă la

schimbarea sistemului de referință

dilatarea duratelor fie două evenimente

care în sistemul de referință propriu

al unui sistem fizic pe care tocmai

le am introdus cel legat de sistemul

fizic au loc în aceeași poziție

Deci x01 este egal cu x 0 2 Dar

la un interval temporal de el tot

a 0 diferit de 0 Spre exemplu în

același loc în aceeași poziție

din sistemul de referință propriu

al unui pistol tragem două focuri

de pistol Deci în același loc vor

01 va fi egal cu zero doi tragem

la două momente diferite 01602

două focuri de pistol Deci obținem

aceste două evenimente exemplu

acest semn acest sistem se deplasează

cu o viteză V față de alții stent

de referință inerțial De ce avem

exprimi și ies pe care le am considerat

întotdeauna în lecțiile de teoria

relativității restrânse aceste

două evenimente vor avea loc în

coordonatele x 1 și 1 și respectiv

X2 și T2 aplicăm transformărilor

s pentru a calcula Delta teză Deci

delta 0 acestea tată 0 în transformările

lor sa fie egal cu gama mulți cu

T 2 minus vpc pătrat x 2 minus

gama de 1 minus vpc pătrat X1 Am

aplicat transformările lorentz

între evenimentele din sistemul

de referință s 0 care este 9 exprime

vechiul athlean devine acestea

0 relativ la sistemul de referință

SC obținem că Delta t 0 este gama

de el tot a gama te 2 minute 1

minus gama vpc pătrat x 2 minus

x 1 care este Delta x dar Delta

X 0 după cum am spus este egal

cu 0 Deci trebuie să folosim și

o această informație faptul că

evenimentele au loc în același

punct obținem Deci că gama x 2

minus vt2 minus gama X1 minus vt1

este egal cu 0 rezultă Delta x

adică gama x 2 minus x 1 este egal

cu Gamma Delta Delta t fiinte 2

minute În această relație putem

simplifica factorul comun ca ma

și obținem că în acest caz particular

Delta X 0 este egal cu 0 Delta

x va fi egal cu v ori de el tate

pe care putem să îl înlocuim în

această ecuație deci putem înlocui

Delta x aici și obținem că Delta

t 0 în acest caz particular va

fi egal cu gama factorul comun

gama înmulțit cu factorul comun

de el tot a obține și factor comun

Delta t m și mulți cu această mărime

1 din partea stângă minus ne rămâne

V pătrat împărțit la c pătrat Dar

prin definiție a lui gama Deci

mai exact prin notații gama este

o notație noi definiție De ce am

notat cu gama mărimea 1 împărțit

la radical din 1 minus z pătrată

împărțit la c pătrat și Deci 1

minus b pătrat pe ce pătrat este

egal cu 1 pe gama la pătrat deci

de tate zero va fi egal cu gama

înmulțit cu unul pe gama la pătrat

înmulțit cu Delta t simplificăm

gama și de obținem că Delta t este

egal cu Gamma Delta teză aceasta

este relația care Stabilește dilatarea

duratelor față de durata proprii

a unui proces fizic pentru că Delta

t va fi întotdeauna mai mare decât

Delta d 0 și asta înseamnă că durata

unui proces fizic apare minimă

în sistemul de referință propriu

de chin orice alt sistem de referință

vom face măsura măsurarea sau măsurătoarea

unui duratei unui proces fizic

vom obține o durată mai mare aceasta

este din nou după cum am discutat

doar aparent această se întâmplă

doar apare în sensul că efectul

se datorează diferenței sistemului

de referință în care se face măsurătoarea

în sine procesul durează la fel

nu variază durata ci doar felul

în care îl măsurăm noi felul în

care observăm această durată variază

de la un sistem de referință la

În limita vitezelor mult mai mici

decât viteza de propagare a luminii

în vid Deci Aplicând acest principiu

de corespondență despre care am

vorbit în lecția trecută gama de

vine aproximativ egale și atât

spațiul cât și timpul de redivan

absolut aceasta este foarte important

am spus că în teoria relativității

restrânse timpul și spațiul sunt

relativă dar în mecanica clasică

R sunt absolute De asemenea în

spus că mecanica clasică este un

caz particular al teoriei relativității

restrânse și de și trebuie să obținem

această proprietate de a fi absolute

a spațiului și timpul și a timpului

între anumită limită și anume limita

viteză lor foarte mici și întradevăr

în această limită gama de vine

egal cu 1 și atunci Delta t este

egal cu Delta t 0 și el este egal

cu el 0 sculați Deci spațiul și

timpul redevin absolute în mecanica

clasică după cum știm un alt comentariu

foarte important este că acest

această ecuație la fel ca și celelalte

a fost verificată experimental

mai exact sau obținut următoarea

confirmare experimental dacă se

măsoară timpul de viață al unei

particule instabile și relativiste

Adică o particulă care se dezintegra

după un anumit timp omoare care

timp ia se dezintegrează și are

o viteză comparabilă apropiată

de viteza luminii observăm că acest

timp de viață crește cu viteza

particule deci știm că o particulă

oarecare care se dezintegrează

în repaus îi trebuie o durată o

anumită durată să îi zic să mă

0 atunci dacă o accelerăm foarte

puternic Deci imprimăm o viteză

foarte mare comparabilă cu viteza

luminii și măsurăm din nou timpul

necesar dezintegrării vedem că

el întradevăr crește cu acest Factor

gama acest procedeu proces se observă

acceleratoarele de particule precum

cel construit la San în Geneva

Deci ce vedeți în această imagine

este schema acceleratorului la

și ții la drum colaj dur un accelerator

de particule imens schema lui este

prezentată pentru a vedea mărimea

acestui accelerator de particule

comparată cu orașul Geneva Deci

acest accelerator se află sub orașul

Geneva din Elveția schema este

acest cerc și vedeți mărimea acceleratorului

de particule comparată cu orașul

în sine și Spre exemplu cu pistele

de aterizare ale aeroportului Geneva

De ce este un accelerator imens

de particule în care se pot obține

viteze și se obțin viteze comparabile

cuteza lumini și se pot face astfel

de măsurători