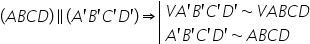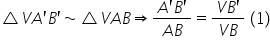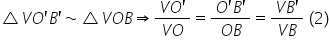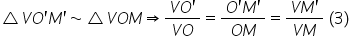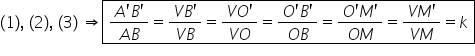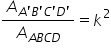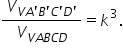Corpuri geometrice asemenea

în continuare să vedem Ce înțelegem

prin corpuri geometrice asemenea

și mi se dă o piramidă nu are importanță

Dacă ea este o piramidă patrulateră

regulată sau piramidă triunghiulară

regulată știind că dacă între o

piramidă dacă secționam o piramidă

cu un plan paralel cu bază atunci

secțiunea care se obține acest

poligon este asemenea cu baza piramidei

mai mult pentru că acest plan a

prim b prim c prim D prim Deci

planul determinat de acest poligon

este paralel cu planul bazei adică

cu planul a b c d din această cauză

rezultă că avem de fapt două piramide

asemenea și anume piramida mică

aceasta este asemenea cu piramida

dată inițial Deci piramida V a

prim b prim e prim D prim Este

asemenea cu piramida V a b c d

de vreme ce vorbim de corpuri asemenea

înseamnă că putem să vorbim de

segmente omul lua de suprafețe

omul luat și de raport de asemănare

mai întâi Haideți să trecem pe

figură elementele pe care le am

învățat la piramida patrulateră

regulată dar și la trunchiul de

piramidă patrulateră regulată Iată

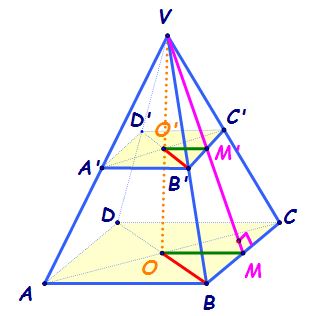
și avem aici piramida mică a prim

b prim c prim D prim și trunchiul

de piramidă Care este desenat aici

am notat cu o punctul de intersecție

al diagonalelor bazei mari o prim

este punctul de intersecție al

diagonalelor bazei mici si mai

avem m este mijlocul segmentului

BC asta înseamnă că vm este apotema

piramidei în același timp m p este

mijlocul segmentului b prim c prim

D prim este apotema piramidei mici

și m prim m este apotema trunchiului

de piramidă mai avem că o m este

apotema bazei mari a trunchiului

o prim m prim este apotema bazei

mici a trunchiului de piramidă

o b este raza cercului circumscris

bazei mari o prim b prim este raza

cercului circumscris bazei mici

și mai avem că v o este înălțimea

piramidei mari V oprim este înălțimea

piramidei mici și o prim o acestei

mint perpendicular pe cele două

baze Este evident înălțimea trunchiului

de piramidă să vedem acum ce segmente

omul luat Avem să dăm câteva exemple

și avem a prim b prim este un segment

omolog cu a b Deci trecem aici

cu AB alte segmente omul wage de

cea mai vut a prim b prim cu AB

mai putem să trecem BB prim cu

b b b b prim acest segment cu v

b sau o prim b prim cu OB Evident

noi dăm doar câteva exemple să

nu mai multe mai avem o prim m

prim cu om aici avem paranteză

cu o m Sau v m prim cu b m și eu

zic că le am enumerat pe cele importante

Evident mai avem și b prim c prim

cu b c c prim D prim cu c d și

așa mai departe să ne gândim acum

la suprafețe omul luată ce suprafețe

omul luat Avem Păi avem pătratul

a prim b prim c prim D prim pentru

ca aici vorbim de un pătrat a prim

b prim c prim D prim cu pătratul

a b c d cu acest pătrat alte suprafețe

omoloage triunghiul V a prim b

prim de cea chest triunghi suprafața

acestui triunghi cu suprafața triunghiului

vab voi nota așa triunghiul V a

prim b prim cu triunghiul abe sau

suprafața triunghiului prim m prim

cel de aici cu vom Deci triunghiul

o prim m prim cu triunghiul v o

m sau triunghiul suprafața triunghiului

v o prim b prim acesta o prim b

prim cu cine cu triunghiul suprafața

triunghiului b o b și așa mai departe

si important acum este raportul

de asemănare ca să găsim raportul

de asemănare Haideți să vedem ce

triunghiuri asemenea avem pe figură

și putem să începem cu triunghiurile

V a prim b prim asemenea cu triunghiul

V a b pentru că a prim b prim e

paralelă cu a b De ce avem așa

triunghiul abe pardon sau va prim

b prim asemenea cu veab mai întâi

trecem pe acesta și ce raport de

asemănare vom obține pe chiar Haideți

să scriu aici a prim b prim supra

ab a prim b prim supra a b pentru

că ele sunt segmente omoloage este

egal cu b b prim supra vb Deci

v b prim supra b egal fie Dan mai

departe și cu va primi supravegheat

dar momentan descriem doar pe acestea

doar bun dacă luăm alta triunghiuri

asemenea de exemplu să luăm triunghiul

v o prim b prim acest triunghi

cu triunghiul b o b Deci triunghiul

v o prim b prim asemenea cu triunghiul

f o b ce vom obține trecem aici

Păi rezultă că vo prim supra V

Deci V8 prim supra v o Cu cât este

egal cu o prim b prim supra o b

o prim b prim supra ab egal mai

departe cu B B prim supra v b v

b prim supra b însăși Observă raportul

v b prim supra verbe acesta se

regăsește și aici deci putem trece

în continuare egal cu și cu aceste

două rapoarte Adică o prim supra

b egal mai departe cu o prim b

prim supra OB bun și Ade să șterg

aici ca să nu fie foarte încărcată

scrierea alte triunghiuri asemenea

si mai putem să alegem Păi mai

putem să alegem triunghiurile v

o prim m prim acest cu triunghiul

v o m Bun deci triunghiul v o prim

m prim asemenea cu triunghiul v

om pentru că și o prim m prim este

paralelă cu oe și ce rapoarte vom

avea vreo prim supra Vio Vio prim

supra y este egal cu o prim n prim

supra om și egal mai departe cu

v m prim supra a m m prim supra

vm dar iată că din nou un raport

de aici este egal cu un raport

de aici deci putem să trecem în

continuare egalitate cu o prim

m prim Deci cu aceste două rapoarte

avem o prim m prim supra Poem este

egal și cu v m prim supra vm evident

că putem să continuăm pentru că

avem în continuare egal cu b prim

c prim supra b c același lucru

se întâmplă și cu această față

vbc a piramidei avem b prim c prim

asemenea cu triunghiul vbc deci

putem să scrie mai departe egal

cu b prim c prim supra b c egal

cu c prim D prim supra DC și așa

mai departe egal cu puncte puncte

și cu bc prim supra b c Cetera

tot ce obținem aici De fapt oricare

rapport din acest șir de rapoarte

egale reprezintă raportul de asemănare

al corpurilor geometrice deci putem

să notăm egal cu k&k este raportul

mai pe scurt așa de asemănare în

continuare să facem două observații

foarte importante prima observație

ne spune că pentru o pereche de

piramide asemenea raportul ariilor

a două suprafețe omul lua de este

egal cu pătratul raportului de

asemănare poate cuvinte dacă avem

de calculat raportul ariilor bazelor

notăm așa aria pătratului a prim

b prim c prim D prim a prim b prim

c prim D prim supra aria pătratului

a b c d va fi egală cu pătratul

raportului de asemănare cu alte

cuvinte cu a prim b prim supra

a b a prim b prim supra a b totul

la pătrat egal mai parte Haideți

să mai scriem încă un raport cu

vm prim supra avem totul la pătrat

m prim supra avem totul la a doua

oricare din rapoartele pe care

le am vrut atunci când am discutat

despre raportul de asemănare cu

alte cuvinte egal de fapt cu pătratul

raportului de asemănare sau putem

să avem raportul ariilor altor

suprafețe omologe de exemplu raportul

ariilor triunghiului V a prim b

prim triunghiul V a prim b prim

Deci ne referim la aria acestui

triunghi supra aria triunghiului

V a B aria triunghiului V a b c

și raportul acesta este egal tot

cu pătratul raportului de asemănare

sau egal mai departe cu raportul

altor suprafețe de exemplu aria

triunghiului v o prim m prim supra

aria cărui triunghi supra aria

triunghiului om aria triunghiului

v om egal tot așa mai departe și

cu să mai dăm un alt exemplu aria

triunghiului V a prim b prim o

prim b prim supra aria cărui triunghi

Păi aria triunghiului v o b pentru

ca aceste două suprafețe sunt suprafețe

omul lege și așa mai departe putem

să întâlnim și alte rapoarte toate

fiind egal cu pătratul raportului

de asemănare Deci cu k la pătrat

de observație se referă la raportul

volumelor astfel Raportul volumelor

a două piramide asemenea este egal

cu cubul portului de asemănare

Deci dacă facem raportul dintre

volumul piramidei mici Deci volumul

piramidei V a prim b prim c prim

D prim supra volumul piramidei

mari adică V a b c d acestora port

este egal cu cubul raportului de

asemănare adică este egal cu a

prim b prim supra ab totul la a

treia sau putem să trecem că egal

cu raportul v o prim supra v o

o prim supra b totul la a treia

și așa mai departe trecem raportul

care ne ajută cel mai mult în rezolvare

a problemei pentru ca aceste observații

ne vor ajuta în rezolvarea unor

probleme de sigle de fapt cu cubul

raportului de asemănare și acum

să facem o aplicație foarte simplă

și anume În Pro piramidă patrulateră

regulată Se consideră o secțiune

a prin b prin c prin d prin paralelă

cu baza să determinăm lungimea

muchiei laterale a tetraedrului

format Dacă raportul volumelor

piramidelor asemenea se subînțelege

este egal cu 1 supra 27 și muchia

laterală a piramidei este de 15

cm Deci știind că planul a prim

b prim c prim D prim este paralel

cu planul a b c d asta înseamnă

că avem două piramide asemenea

și anume V a prim b prim c prim

D prim această piramidă este asemenea

cu piramida vabcd bun să determinăm

lungimea muchiei laterale a tetraedrului

format Deci vrem să determinăm

lungimea segmentului b prima b

sau a 1-a oricare dintre acestea

4 căzi pentru că ele sunt congruente

știind că raportul volumelor piramidelor

asemenea este egal cu 1 supra 27

și muchia laterală a piramidei

adică v b este de 15 cm bun poate

cuvinte știm Care este lungimea

piramidei date inițial Deci v b

are 15 cm și mai cunoaștem că raportul

volumelor piramidelor V a prim

b prim c prim D prim supra volumul

piramidei V a b c d este egal cu

cât cu 1 supra 27 Păi ce raport

de asemănare vom trece Care este

convenabil de vreme ce noi Trebuie

să aflăm lungimea segmentului B

prim b și știm lungimea sa mentului

vb acest raport de asemănare verde

prim supra v b d c egal mai departe

cu v b prim supra Vb la ce putere

la a treia pentru că vorbim de

raportul volumelor mult și știind

că acest raport este egal cu 1

supra 27 Adică 1 pe 3 totul la

a treia ce am obținut avem egalitate

de două puteri care au același

exponent înseamnă că și bazele

sunt egale Deci rezultă că avem

așa raportul v b prim supra b este

egal cu acest raport 1 supra 3

Păi ce rezultă mai departe noi

știm că v b este de 15 cm d rezultă

că B B prim supra 15 ne dă 1 supra

3 Păi asta înseamnă că v b prim

Cu cât este egal avem aici 15 pe

3 adică 5 cm Ce vrem noi să aflăm

noi vrem lungimea segmentului B

prim b dar B prim b Cu cât este

egal cu v b minus b b prim Deci

avem lungimea segmentului v b minus

lungimea segmentului a b prim adică

15 minus 5 cm iar t și obținem

10 cm aceasta fiind lungimea muchiei

tetraedrului deci putem să trecem

așa că bebe prima aici trebuia

să scriem bebe prim Iată este egal

cu are lungimea egală 10 cm si

sunt tot ce am expus legat de segmente

omul Weiss de suprafețe omologe

precum și de rapoarte de asemănare

pentru o piramidă patrulateră regulată

să știți că se aplică și în cazul

unei piramide triunghiulare regulate

sau a unei piramide hexagonale

regulate