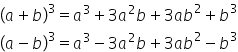Cubul sumei și al diferenței

să vedem acum Ce formulă vom obține

pentru cubul unei sume precum și

pentru cubul unei diferențe și

avem aici o sumă de două numere

reale să notăm că a și b sunt numere

reale și vrem să calculăm cubul

acestei sume Păi cum putem să exprimăm

Cubul unui număr putem să îl scriem

ca fiind produsul dintre numărul

respectiv în cazul nostru această

sumă și pătratul său adică pătratul

acestei sume și vom avea a plus

b înmulțit cu avem aici o sumă

de doi termeni ridicată la pătrat

deja am aceste formule se cunosc

din clasa a șaptea nu voi insista

a pătrat adunat cu 2 a b adunat

cu de pătrat vrem să desfacem acum

parantezele Deci fiecare termen

din prima paranteză se va înmulți

cu fiecare din a doua avem a ori

a la a doua înseamnă a la a treia

a adunat cu a ori 2ab Deci 2 a

b adunat cu a înmulțit cu B pătrat

bun absolut același lucru îl vom

face și pentru b b înmulțit cu

a la a doua adunat mai departe

cu b înmulțit cu 2ab și în final

avem b ori b pătrat adică b la

a treia a la 3 adunat cu peste

deja putem să mai calculăm a înmulțit

cu 2 ori a ori b Păi a ora înseamnă

a pătrat Deci vom avea 2-a pătrat

b adunat cu AB pătrat adunat mai

departe cu Haide să trecem mai

întâi tot litera a adică a pătrat

b adunat aici cu b ori b înseamnă

b pătrat de cea bem 2 ori a de

pătrat plus b la a treia bun Deci

avem la adunat cu mai putem să

facem câteva calcule pentru că

Iată aici Avem doi a pătrat b și

aici avem A pătrat b iar Aici avem

AB pătrat și aici 2ab pătrat adunând

acest termen da cu acesta de fapt

adunăm 2 cu 1 ne dă 3-a pătrat

b adunat cu AB pătrat plus de două

ori a b pătrat înseamnă 3-a b pătrat

adunat în final cu b la a treia

de ceai de sănătăuca avem A plus

B totul la a treia la date exact

ce am trecut aici chiar putem să

încadrăm am un ținut formula pentru

cubul unei sume de două numere

reale acum cum vrei cinema ceastă

formula păi în primul rând putem

să observăm faptul că termenii

pe care îi am obținut sunt termen

de gradul al treilea avem aici

a la a treia aici avem un produs

dintre un număr ridicat la a doua

și 1 ridicat la întâia Deci avem

un termen de gradul al treilea

la fel și aici la fel și aici deci

a adunat cu b totul la a treia

a dat primul termen ridicat la

a treia Da adunat cu de trei ori

pătratul primului termen înmulțit

cu al doilea termen adunat mai

departe cu de trei ori primul termen

înmulțit cu pătratul celui de al

doilea termen și adunat în final

cu al doilea termen ridicat la

a treia dacă vrem să calculăm acum

cubul diferenței adică a minus

b totul la a treia Păi fie putem

să facem calculul cum am făcut

mai sus sau putem să îl facem direct

Folosind un an de această formulă

iată în loc de ei îl vom avea de

fapt tot pe ei însă în loc de B

îl avem pe minus b aceasta este

diferența între cele două formule

și Haideți să notăm avem a la a

treia Cum este aici adunat cu trei

a pătrat în loc de B îl trecem

pe minus b înmulțit cu minus b

adunat cu 3 ori a înmulțit cu minus

b pardon Deci cu minus b totul

la pătrat adunat cu minus b la

a treia și ai de să vedem ce am

obținut avem aici A 3-a aici avem

un număr pozitiv avem Semnul plus

înmulțit cu semnul minus de de

de fapt minus 3 a pătrat b adunat

cu 3 ori a a minus b la a doua

Nevada b la a doua și ai semnul

minus ridicat din nou la un exponent

impar va ieșit din fața parantezei

Deci avem minus b la a treia și

avem a minus b totul la a treia

nea dat ce am obținut aici acum

Unde își face simțită prezența

semnul minus dar din fața lui minus

b Păi semnul minus a apărut la

acei termeni care conțin care îl

conțin pe b la un exponent impar

Iată aici exponentul lui b este

1 și na apărut semnul minus aici

exponentul lui b este 3 tot număr

impar și ne apărut semnul minus

aici unde e b a fost ridicat dau

un exponent par am avut de fapt

minus b la a doua semnul minus

a dispărut Da și neamul și na rămas

aici în Semnul plus a minus b totul

la a treia ne dă a treia minus

3 pătrat b adunat cu 3 a b pătrat

minus b la a treia și acum mai

de să aplicăm aceste două formule

și să calculăm 2 plus radical din

5 totul la a treia Păi fiind aici

o sumă înseamnă că vom aplica prima

formulă în prima formulă putem

să observăm că peste tot avem Semnul

plus deci nu trebuie să ne mai

facem griji pentru semnul minus

Camila diferență și avem primul

termen ridicat la a treia Deci

2 la a treia adunat cu de trei

ori pătratul primului termen de

2 la a doua înmulțit cu al doilea

termen radical din 5 plus 3 înmulțit

cu primul termen adică 2 înmulțit

cu pătratul celui de al doilea

termen radical din 5 la pătrat

înmulțit cu ultimul termen adică

al doilea termen ridicat la a treia

și facem calculul 2 la a treia

înseamnă 8 adunat cu 2 la a doua

ori 312 radical din 5 plus 3 ori

2 6 înmulțit cu radical din 5 la

pătrat înseamnă 5 plus aici avem

radical din 5 la a treia apoi putem

să îl scriem radical din 5 la pătrat

ora de cal din 5 de fum avea aicea

5 radical din 5 Haide să ștergem

5 radical din 5 și în sumă iar

Aici avem șase ori 5:30 cu 838

adunat cu 12 radical din 5 plus

5 radical din 5 adunăm 12 cu 517

radical din 5 și am făcut acest

calcul această cubul acestei sume

următorul exercițiu 4 minus radical

din 3 la a treia pe având aici

o diferență înseamnă că vom aplica

cea de a doua formulă de să fim

atenți la semn acolo unde le apare

semnul minus și avem primul termenii

Dic ala a treia Deci 4 la a treia

apoi de trei ori pătratul primului

termen de 3 ori 4 la a doua înmulțit

cu al doilea termen Deci cu radical

din 3 Cum acest termen este la

exponentul 1 înseamnă că o să ne

apară e semnul minus ta ca în formulă

apoi de trei ori primul termen

înmulțit cu pătratul celui de al

doilea termen adică radical din

3 la a doua Cum ne apare aici o

putere pară înseamnă că vom avea

Semnul plus la piață corespondența

cu formula și avem apoi acest termen

indicat la a treia avem o putere

impară Deci ne apare minus radical

din 3 la a treia și acum facem

calculul 4 la a treia ne dă 64

minus 4 la a doua 16 ori 348 radical

din 3 plus aici ne dă 3 înmulțit

cu 3 9 ori 4 36 minus radical din

3 la a treia înseamnă 3 radical

din 3 și facem calculul 64 cu 36

înseamnă 100 minus 48 radical din

3 adunat cu minus 3 radical din

3 ne dă minus 51 radical din 3

următorul exercițiu 1 supra 3x

minus 2 totul la a treia avem tot

așa diferență de ce aplicăm a doua

formulă și avem primul termen ridicat

la a treia 1 supra 3x acesta e

primul termen totul la a treia

apoi avem de trei ori primul termen

ridica la pătrat Deci 1 supra 3x

ridicat la pătrat înmulțit cu al

doilea termen de ciclu 2 cum Acesta

are exponentul 1 semne că aici

ne apare semnul minus apoi de trei

ori primul termen 1 supra 3 x înmulțit

cu al doilea termen indicat la

a doua de 2 la a doua putere par

înseamnă că aici avem plus și vino

album avea minus acest termen la

a treia adică 2 la a treia 1 supra

3 înmulțit cu x totul la a treia

înseamnă că fiecare Factor al acestui

produs se ridică la a treia și

vom avea 1 supra 27 x la a treia

minus avem aici 3 înmulțit cu acest

produs să ridicăm la pătrat Deci

1 supra 9x pătrat înmulțit cu 2

adunat cu avem trei ori 1 supra

3 înmulțit cu x înmulțit cu 2 la

a doua Păi aici putem să simplificăm

ne dă unul și unul nu mai scriu

să nu încărcăm notația și avem

4x Deci plus 4 ori x minus 2 la

a treia 8 și avem 1 supra 27 x

la a treia tata 16 m să simplificăm

prin trei aici ne rămâne 1 și aici

în Nevada 3 Deci Haideți să ne

uităm o să ne dea 2 supra 3 x pătrat

plus 4x minus 8 și sa încheiat