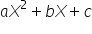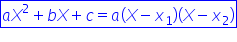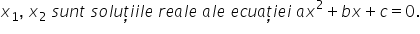Descompunerea trinomului de gradul II

în această lecție o să discutăm

despre descompunerea trinomului

de gradul al doilea un om este

o expresie algebrică ce are trei

componente ia tele ax pătrat b

x și c Așadar trinomul de gradul

al doilea are forma ax pătrat plus

bx plus c iar dacă egalăm acest

trinom cu 0 se obține ecuația atașată

trinomului ax pătrat plus bx plus

c egal cu 0 Aceasta este o ecuație

de gradul al doilea iar în cazul

în care Delta este mai mare sau

egal cu 0 ecuația admite de rădăcini

reale pe care le notăm cu X1 și

X2 are loc următoarea descompunere

a trinomului în polinoame de gradul

întâi sau un factor vineri ax pătrat

plus bx plus c este egal cu a pe

lângă x minus x 1 pe lângă x minus

x 2 nu folosi această formulăm

atunci când trebuie să descompunem

în factori expresia algebrice sau

când dorim să simplificăm fracții

ce au la numărător și la numitor

un trinom de gradul al doilea Haideți

să demonstrăm această formulă ax

pătrat plus bx plus c egal 2 Da

factor comun pe a și avem A pe

lângă x la pătrat plus b supra

a x plus c supra a egal înainte

de a continua aș vrea să vă reamintesc

Relațiile lui viet pentru că o

să le folosim aici suma rădăcinilor

ecuației de gradul al doilea X1

plus X2 este egală cu minus b supra

a iar produsul rădăcinilor X1 X2

este egal cu c supra A deci suma

este minus b supra a și atunci

minus esti va fi egal cu b supra

a iar produsul rădăcinilor este

c supra a prin urmare în această

paranteză în loc de b supra a voi

scrie minus s iar în loc de C supra

am avem produsul celor două rădăcini

Prin urmare avem A pe lângă x la

pătrat minus x plus b egal cu a

pe lângă x la a doua minus acum

în loc de s o să scriu X1 plus

X2 totul ori x plus x 1 x 2 egal

acum desfac paranteza rotundă a

pe lângă x la a doua minus x 1

x minus x 2 x plus x 1 x 2 egal

cu ei pe lângă din primii doi termeni

îl dăm factor comun pe x x pe lângă

x minus x 1 minus din ultimii doi

îl dă factor comun pe x 2 x 2 pe

lângă x minus X1 egal Acum putem

se dă factor comun paranteza x

minus x1a de lângă x minus x 1

pe lângă x minus X2 Iată am demonstrat

formula scrisă mai sus și acum

să facem o aplicație avem următorul

exercițiu se cere să simplificăm

expresia 2x la a doua minus 5x

plus 3 supra 6 x la a doua plus

x minus 15 observăm că atât la

numărător cât și la numitor avem

un drum de gradul al doilea Așadar

vom rezolva mai întâi ecuațiile

atașat a acestora începem cu primul

trinom ecuația atașată va fi 2

x pătrat minus 5x plus 3 egal cu

0 Delta este b pătrat minus 4 ace

adică minus 5 la pătrat minus 4

ori 2 ori 3 egal cu 25 minus 8

ori 324 și egal cu 1 prima rădăcină

X1 va fi minus b adică 5 minus

radical din Delta 1 supra 2 a 2

ori 2 4 4 supra 4 egal cu 1 a doua

rădăcină X2 va fi minus b adică

5 plus radical din deltă supra

2-a avem 6 supra 4 egal cu 3 pe

2 prin urmare acest trinom 2x la

pătrat minus 5x plus 3 se descompune

astfel 2 pe lângă x minus prima

rădăcină 1 pe lângă x minus cea

de a doua rădăcină 3 pe 2 egal

în a doua paranteză aducem la numitor

comun avem 2 pe lângă x minus 1

pe lângă 2x minus 3 totul pe 2

egal se simplifică 2 și obținem

x minus 1 pe lângă 2x minus 3 Așadar

2x la pătrat minus 5x plus 3 se

va scrie x minus 1 pe lângă 2x

minus 3 am descompus în factori

liniari Express de la numărător

continuăm cu al doilea trinom ecuația

atașată acestuia este 6 x pătrat

plus x minus 15 egal cu 0 Delta

este b pătrat Adică 1 minus 4 ori

a ori c 6 ori minus 15 egal 6 8

15 este 90 90 x 4 360 Plus 1 361

X1 este minus b adică minus 1 plus

radical din deltă supra 2-a 2 ori

6 egal cu minus 1 plus radical

din 361 este 19 totul supra 12

egal cu 18 supra 12 mai simplificăm

cu șase și obținem trei pe doi

a doua rădăcină X2 este minus 1

minus 19 supra 12 egal cu minus

20 supra 12 se simplifică cu 4

și obținem minus 5 supra 3 Așadar

trinomul 6 x la a doua plus x minus

15 se descompune în 6 pe lângă

x minus prima rădăcină 3 pe 2 pe

lângă x minus a doua rădăcină atenție

a doua rădăcină este minus 5 pe

3 Deci o să avem plus 5 supra 3

în paranteze aducem la numitor

comun o să avem 6 pe lângă 2x minus

3 pe 2 pe lângă 3x plus 5 pe 3

egal acest 6 se simplifică cu 2

și cu 3 și obține m în final 2x

minus 3 pe lângă 3x plus 5 voi

continua mai jos 6 x la a doua

plus x minus 15 se descompune în

2x minus 3 pe lângă 3x plus 5 și

acum Revenim la fracția inițială

pe care o să mai scriu încă o dată

2x la a doua minus 5x plus 3 supra

6 x la a doua plus x minus 15 egal

la numărător avem x minus 1 pe

lângă 2x minus 3 supra 2x minus

3 pe lângă 3x plus 5 se simplifică

2x minus 3 cu 2x minus trei și

a final obținem x minus 1 supra

3x plus 5