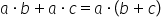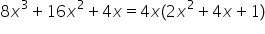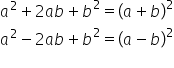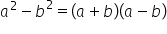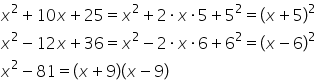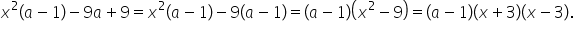Descompuneri în factori

descompunerea în factori descompunerea

în factori este operația inversă

înmulțirii a descompune o expresie

algebrică factori înseamnă a o

scrie ca un produs de două sau

mai multe expresii algebrice mai

multe metode de a descompune în

factori expresia prima dintre acestea

este metoda factorului comun avem

de exemplu următoarea expresie

5 x plus 5 y în acest caz Aplicând

proprietatea de distributivitate

a înmulțirii față de adunare în

varianta inversată și anume Trebuie

să identificăm un factor comun

al tuturor termenilor expresiei

date observăm că acest factor comun

este 5 și vom scrie egal cu 5 pe

lângă x plus y plus z observăm

Așadar că am transformat suma algebrică

pentru un produs Deci am descompusă

în factori un al doilea exemplu

8 x la a treia plus 16 x la a doua

minus 4x la a patra observăm că

acești trei termeni conțin factorul

comun 4 și de asemenea mai au și

factorul comun x la a doua adică

x la puterea cea mai mică Și atunci

vom da factor comun pe 4x la a

doua A da factor comun înseamnă

a împărțit fiecare termen la acel

factor comun 8 x la a treia împărțit

la 4 x la a doua este 2 x 16 x

la a doua împărțit la 4 x la a

doua este 4 iar 4x la a patra împărțit

la 4 x la a doua este x la a doua

observăm că în paranteză nu mai

putem da factor comun și atunci

această descompunere va rămâne

sub această formă punctul c 5 pe

lângă 2x minus 3 minus x pe lângă

2x minus 3 observăm că factorul

comun este expresia 2x minus 3

Și atunci vom scrie egal cu 2x

minus 3 pe lângă 5 minus x o ador

metodă de descompunere a expresiilor

algebrice în factori este metoda

folosirii formulelor de calcul

prescurtat să ne reamintim aceste

formule de calcul prescurtat a

plus b la a doua este egal cu a

la a doua plus doi a b plus b la

a doua a minus b la a doua este

egal cu a la a doua minus 2ab plus

b la a doua și a plus b pe lângă

a minus b este egal cu a la a doua

minus b la a doua avem următoarea

expresie x la a doua plus 10x plus

25 metoda factorului comun nu se

poate aplica deoarece acești trei

termeni nu au un factor comun primii

doi termeni ar avea factorul comun

x însă 25 nu îl conține pe x și

atunci el va folosi prima metodă

Încercăm să evidențiem în această

expresie pătratele unor numere

reale astfel încât să putem folosi

prima formulă de calcul prescurtat

observăm că x la a doua este pătratul

lui x 25 este pătratul lui 5 iar

10 x este produsul dintre 2x și

5 Și atunci vom scrie astfel x

la a doua plus doi ori x ori 5

plus 5 la a doua și atunci avem

condițiile acestei formule de calcul

prescurtat are se va restrânge

sub forma x plus 5 totul la a doua

What do expresie x la a doua minus

12x plus 36 să evidențiem pătratele

unor numere x la a doua este pătratul

lui x 36 este pătratul lui 6 și

acum verificăm dacă termenul din

mijloc este produsul dintre doi

și ceilalți termeni observăm că

12x înseamnă 2 ori x ori 6 deci

putem aplica a doua formulă de

calcul prescurtat nu scrie dar

în continuare cu x la a doua minus

2 ori x ori 6 plus 6 la a doua

egal mai departe în locul lui a

avem x iar în locul lui b avem

șase Deci vom restrânge această

expresie sub forma x minus 6 totul

la a doua și în al treilea exemplu

x la a doua minus 64 observăm că

avem Diferența a doua pătrate de

numere reale pentru că 64 este

pătratul lui 8 deci putem scrie

egal mai departe cu x la a doua

minus 8 la a doua ne uităm la ultima

formulă de calcul prescurtat observăm

că diferența a două pătrate se

descompune în produsul dintre suma

și diferența celor două numere

aceasta expresia se va scrie x

plus opt pe lângă x minus 8 dețineți

că această formulă se poate aplica

doar în cazul diferenței a două

pătrate nu și în cazul sumei a

două pătrate și o posibilitate

de a descompune expresiile algebrice

în factori este folosirea unor

metode de combinate și anume Gruparea

termenilor artificii de calcul

factor comun sau formule de calcul

prescurtat ne propunem Să descompunem

în factori următoarea expresie

x la a doua plus 5x plus 6 observăm

că nu putem da factor comun pentru

că acești termeni nu au un factor

comun primii doi termeni conțin

factorul comun x însă 6 nu conține

pe x să vedem dacă putem aplica

a doua metodă cea a formulelor

de calcul prescurtat având în vedere

că nu putem evidenția în numărul

6 pătratul unui alt număr real

înseamnă că nu vom putea aplica

formulele de calcul prescurtat

și atunci va trebui să scriem această

expresie sub o altă formă astfel

încât ulterior să putem evidenția

un factor comun să încercăm să

îl scriem pe 5 x ei fiind suma

dintre 4 x și x să vedem dacă ne

ajută această scriere înlocuim

în expresia inițială și obținem

x la a doua plus 4x plus x plus

6 Acum putem da factor comun din

primii doi termeni pe x și scrie

egal cu x pe lângă x plus 4 plus

x plus 6 însă observăm că acum

nu mai putem da factor comun înseamnă

că această scriere a lui 5 x sub

forma a 4 x plus x nu este prea

convenabilă noi Rescrie această

expresie x la a doua plus 5x plus

6 și să încercăm să scriem pe 5

x sub forma 3x plus 2x o să înlocuim

în expresia inițială și obținem

x la a doua plus 3x plus 2 x plus

6 din primii doi termeni Îți dăm

factor comun pe x și obținem x

pe lângă x plus 3 ia din ultimii

doi termeni în factor comun pe

2 și scrie amândoi pe lângă x plus

3 observăm că acum putem continua

descompunerea fiindcă avem factorul

comun x plus 3 și vom putea scrie

egal cu x plus 3 pe lângă x plus

2 așadar am descompus această expresie

în factori Cum putem să găsim mai

ușor modalitatea de a scrie termenul

din mijloc fără să facem prea multe

încercări o regulă ar fi aceasta

atunci când coeficientul lui x

la a doua este 1 Trebuie să găsim

două numere care adunate să dea

5 și înmulțite să dea 6 acestea

sunt în cazul nostru 32 pentru

că 3 plus 2 este egal cu 5 și 3

ori 2 este egal cu 6 și atunci

punând în aplicare această regulă

și anume suma numerelor să dea

coeficientul lui x iar produsul

celor două numere este egal cu

termenul liber vom putea să descompune

mai ușor acestei expresii fără

să folosim prea multe încercări

în continuare vom face câteva exerciții

Descompuneți în factori expresiile

la punctul a o să mai scrii o dată

expresia 7x pe lângă 5x plus 3

plus 14 pe lângă 5x plus 3 observăm

că putem să dăm factor comun expresia

a 5 x plus 3 și vom scrie egal

cu 5 x plus 3 pe lângă 7x plus

14 Acum ne uităm în paranteze să

vedem dacă nu putem să continuăm

descompunerea observăm în a doua

paranteză avem factorul comun 7

Și atunci vom scoate pe șapte factor

comun din a doua paranteză și îl

voi Scrie în fața parantezelor

egal cu 7 pe lângă 5x plus 3 pe

lângă x plus 2 punctul b x la a

doua pe lângă a minus 1 minus 9-a

plus noua dar ultimii doi termeni

conțin un factor comun Și atunci

vom scrie egal cu x la a doua pe

lângă a minus 1 și vom da factor

comun pe minus 9 minus 9 a pe lângă

a minus 1 atenție când îl dăm factor

comun pe minus 9 în paranteză rămâne

minus 1 acum o serveam că putem

să mai dăm factor comun pe n minus

1 și obținem A minus 1 pe lângă

x la a doua minus 9 în a doua paranteză

observăm că avem Diferența a două

pătrate fiindcă 9 este pătratul

lui 3 și atunci folosim această

formulă de calcul prescurtat a

la a doua minus b la a doua se

descompune în A plus B pe lângă

a minus b în cazul nostru a este

X și B va fi 3 și atunci scriem

egal cu a minus 1 pe lângă x plus

3 pe lângă x minus 3 punctul c

5 x plus 1 la a doua minus 4x la

a doua observăm că avem și de data

aceasta Diferența a două pătrate

fiindcă 4x la a doua este pătratul

lui 2 x și atunci putem să folosim

din nou această formulă egal cu

5 x plus 1 la a doua minus 2x la

a doua așa dar am pus în evidență

cele două pătrate și acum aplicăm

formula de calcul prescurtat în

locul lui a noi avem expresia a

5 x plus 1 iar b în cazul nostru

este 2x Așadar vom Descompune în

A plus B pe lângă a minus b adică

5 x plus 1 plus 2x pe lângă 5x

plus 1 minus 2x dar acum facem

calculele în paranteze 5x plus

2 x este 7 x plus 1 ia 5x minus

2x este 3x plus 1 în paranteze

Nu mai putem da factor comun și

nici nu mai putem aplica alte metode

punctul d 16 x la a șasea plus

8 x la a treia plus 1 să încercăm

să evidențiem pătratele unor expresii

observăm că 16 x la a șasea este

pătratul lui 4x la a treia unul

este pătratul lui 1 8 x la a treia

înseamnă produsul dintre 2 ori

4x la a treia ori 1 observăm atunci

că putem să aplicăm această formulă

de calcul prescurtat ala a doua

plus doi a b plus b la a doua se

restrânge sub forma a plus b totul

la a doua Și atunci vom scrie egal

mai departe cu 4 x la a treia totul

la a doua plus 2 ori 4x la a treia

ori 1 plus 1 la a doua am evidențiat

Așadar această formulă acum în

cazul nostru a este prima paranteză

adică 4x la a treia iar b este

150 de L cu 4x la a treia plus

1 totul la a doua și ultimul exercițiu

punctul E x la a doua minus 7x

plus 6 să vedem cum putem să scriem

pe 7 x Încercăm să găsim două numere

care adunate să dea 7 și înmulțite

să dea 6 acestea sunt 6 și 1 pentru

că 6 plus 1 este egal cu 7 și 6

ori unul este egal cu 6 și atunci

pe 7x îl vom Scrie sub forma 6

x plus x și înlocuim în expresia

inițială x la a doua minus sincarom

acest minus vom pune în paranteză

6 x plus x plus 6 acum desfacem

paranteza schimbând semnele numerelor

din paranteză și obținem x la a

doua minus 6x minus x plus 6 din

primii doi din factor comun pe

x și obținem x pe lângă x minus

6 ia din ultimii doi dăm factor

comun pe minus unu și scrie în

minus pe lângă x minus 6 observăm

că avem un factor comun acesta

este x minus 6 deci nu scrie egal

cu x minus 6 pe lângă x minus 1