Determinarea dreptei și a planului

să vedem acum care sunt modalitățile

de determinare a unei drepte și

a unui plan în ceea ce privește

de terminarea dreptei e foarte

simplu știind că avem această axiomă

axiomă dreptei două puncte distincte

determina o dreaptă și numai una

avem aicea că dreapta a b Deci

două puncte distincte determina

o dreaptă unică care sunt acum

modalitățile de a determina un

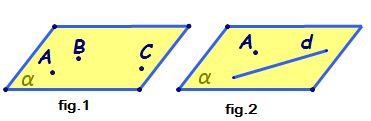
plan Păi avem această axiomă trei

puncte necoliniare determină un

plan și numai unul vorbim de axioma

planului și Mai avem încă trei

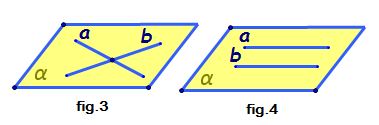
modalități Iată o dreaptă și un

punct exterior ei determină un

plan unic o Vom nota teoremă 1

pentru că aceasta este o axiomă

este o teoremă și chiar o so demonstrăm

sau altă modalitate două drepte

concurente determină un plan unic

și următoarea dar e tot a două

drepte paralele determină un plan

unic și vom demonstra fiecare din

aceste trei teoreme în parte începem

cu teorema 1 o dreaptă și un punct

exterior ei determină un plan unic

și vom trasa o dreaptă să o notăm

cu d mic și un punct exterior ei

în notăm cu A mare ce avem de arătat

trebuie să demonstrăm că există

un plan care conține dreapta d

și punctul A și că acel plan este

unic mai întâi Haideți să notăm

că punctul A nu se află pe dreapta

d deci a nu aparține dreptei D

acum nu știm că o dreaptă este

determinată de două puncte distincte

cu alte cuvinte Pe o dreaptă avem

cel puțin două puncte diferite

Deci fie B și C două puncte care

aparțin dreptei d iar aceste puncte

sunt distincte și chiar de desen

b și c acum cum sunt punctele A

B și C Păi devreme C A nu aparține

dreptei d iar acestea două puncte

sunt distincte e clar că cele trei

puncte sunt necoliniare deci de

aici rezultă că punctele a b și

c sunt puncte necoliniare Ce știm

noi că Determină trei puncte necoliniare

un plan de C rezultă în continuare

din axioma 2 axiomă planului că

există Alfa plan unic determinat

de Haideți să trecem așa plan determinat

crescut teza astfel de punctele

a b și c cu alte cuvinte Alfa e

planul este planul abc acum trebuie

să arătăm că Alfa conține punctul

A și dreapta d apoi e clar că alfako

cine punctul A de ce e Vidin tei

aparține planului Alfa să vedem

acum Cum arătăm că dreapta d este

inclusă în planul alfa Fie punctele

B și C să notăm aici aparțin planului

Alfa asta înseamnă că ce va rezulta

Păi nu știm că din dusei două puncte

distincte între un plan Atunci

înseamnă că dreapta determinată

de ele conținută în totalitate

în planul respectiv deci de vreme

ce aceste două puncte sunt în Alfa

și punctele sunt distincte atunci

rezultă din aceste două relații

conform axiomei notate de noi patru

în lecția în care am discutat despre

axiome că dreapta b c este inclusă

în Alfa bun dreapta BC e chiar

dreapta d deci putem să ștergem

aici și vom trece tot este inclus

în Alfa și atât am obținut că a

aparține planului Alfa și dreapta

d este inclus în Alfa noi trebuie

să arătăm că acest plan alfa care

are aceste două proprietăți este

un plan unic Păi gândim în felul

următor fie gama sau putem să notăm

cum vrem fie gama un plan care

conține punctul A de ce aparține

planului gama și conține și dreapta

d dreapta d inclusă în gama banda

c știm noi despre dreapta d de

vreme ce Ea este un plan înseamnă

că toate punctele A sunt în planul

respectiv asta înseamnă că Deci

rezultă de aici că b și c aparțin

planului gama Deci avem punctele

A B și C în gama Cum sunt cele

trei puncte sunt necoliniare iar

demonstrația o avem aici de să

notăm dar punctele a b și c sunt

necoliniare Păi ce știm noi despre

trei puncte necoliniare conformă

axiomei planului că le determină

un plan unic asta înseamnă că planul

gama în care se află cele trei

puncte este de fapt planul determinat

de punctele a b și c d c egal cu

planul a b c bondar planul ABC

e de fapt planul alfa de ceai de

să notăm aici relația 1 relația

2 deci rezultă din relația 1 și

2 că planul alfa este egal cu gama

Și de aici rezultă că planul alfa

este întradevăr un plan unic Haide

să nu uităm aici că am folosit

tot axioma planului cu alte cuvinte

am arătat că există un Unique plan

care conține dreapta d și punctul

A acest plan se notează astfel

în paranteză trecem dreapta a și

punctul A exterior ei Deci planul

alfa e planul determinat de dreapta

d și d punctul A Să demonstrăm

acum această teoremă Să arătăm

că două drepte concurente determină

un plan unic Deci desenăm două

drepte concurente plantum a mic

și b mic dacă ele sunt concurente

înseamnă că se intersectează un

singur punct să notăm cu M punctul

de intersecție deci a intersectat

cu b este punctul m trebuie să

arătăm că există un plan care conține

dreptele a și b și acel plan este

unic acum pentru dreapta a mic

observăm că am trecut aici punctul

M care aparține dreptei noi știm

că o dreaptă determinată de cel

puțin două puncte distincte asta

înseamnă că putem să alegem pe

dreapta a mic încă un punct exemplu

punctul A mare a mare diferit de

m Deci notăm fie a aparține dreptei

a mic punctul a diferit de punctul

M absolut la fel procedăm pentru

dreapta b mic vom alege aici punctul

B Deci notăm fie punctul B aparține

dreptei b mic iar b este diferit

de punctul M Cum sunt cele trei

puncte m b și a Păi sunt puncte

necoliniare dacă ele ar fi coliniare

seamnă că dreptele a și b ar fi

de fapt dreptei suprapuse ceea

ce e fals pentru că ele sunt drepte

concurente au un singur punct în

comun deci de aici Haideți să facem

o acolada așa mai potrivită de

aici rezultă că punctele a m și

b sunt puncte necoliniare cred

că deja Știți ce urmează rezultă

din axiomei planului axioma notată

de noi doi că există un unic plan

să înotăm Alfa determinat Deci

plan determinat de punctele a m

și b cu alte cuvinte Alfa este

planul a m b acum noi trebuie să

arătăm că acest plan alfa conține

și dreapta a mic și dreapta b mic

Păi punctele a și m sunt în Alfa

Deci notăm a m aparțin planului

Alfa com ele sunt puncte distincte

si va rezulta mie dacă două puncte

se află între un plan atunci dreapta

determinată de ele este inclus

în planul respectiv vorbind de

două puncte diferite Deci rezultă

din axioma 4 că dreapta a m adică

dreapta a mic este inclusă în Alfa

absolut la fel punctele b și m

aparțin planului Alfa Da b și m

ele sunt puncte distincte tot așa

rezultă din aceeași axiomă axioma

4 că dreapta d mic adică dreapta

b m este inclusă în planul alfa

acum trebuie să mai arătăm doar

unicitatea acestui plan Cum arătăm

că Alfa este plan unic este Unicul

plan cu aceste două proprietăți

pe care mai Deci chiar să le subliniem

așa să le Observați Păi vom proceda

ca în demonstrație anterioară fie

gama un plan astfel încât a este

inclus în gama și b este inclusă

în gama pe asta înseamnă că și

punctele că toate punctele b m

și aparțin planului gama Deci din

aceste două relații rezultă că

b m și a aparține planului gama

însă aceste puncte sunt puncte

necoliniare Haideți să copiem ce

am scris aici De ce le sunt puncte

necoliniare Ce rezultă prin urmare

conform axiomei planului noi știm

că trei puncte necoliniare determină

un plan unic Deci înseamnă că planul

gama e de fapt planul determinat

de aceste trei puncte Deci rezultă

că gama e planul a m b care de

fapt lanul Alfa și astfel am arătat

că orice alt plan care conține

cele două drepte a și b e de fapt

egal cu planul alfa asta înseamnă

că există un unic plan un singur

plan care conține dreptele a și

b și notăm astfel planul determinat

de dreptele a mic și b mic ultima

teoremă este teorema 3 în care

ni se spune că două drepte paralele

determină un plan unic nu îmi face

toată demonstrația am dat câteva

elemente ale demonstrației Deci

Considerăm două drepte d și d prim

și aceste două drepte sunt drepte

paralele trebuie să arătăm că există

un plan care le conține și că acel

plan este unic acum Ce înseamnă

drepte paralele pe două drepte

sunt paralele dacă ele se află

în același plan și nu au nici un

punct în comun Deci din definiția

dreptelor paralele rezultă că există

un plan alfa care conține cele

două drepte deci a astfel încât

de este inclus în Alfa și D prim

Este pardon Haide să se vadă că

am scris aici D prim Este inclusă

tot în planul alfa un trebuie să

ai acest plan alfa este unic pe

Ce știm despre acest lac ideea

de rezolvare e următoarea trebuie

să alegem pe aceste două drepte

trei puncte alegem aici un punct

să îi spune ma și aici putem Alege

două puncte B și C evident că dreptele

fiind paralele punctele a b și

c sunt Ce fel de puncte sunt necoliniare

atunci cum aceste puncte se află

și în planul alfa a b și c aparțin

planului Alfa și ele sunt necoliniare

înseamnă că din axioma planului

notăm axiomă 2 că planul alfa e

de fapt lanul determinat de punctele

a b și c acum trebuie să arătăm

că orice alt plan care îndeplinește

cele două condiții a de fapt egal

cu planul alfa Deci Considerăm

gama un plan a astfel încât și

dreapta d este inclusă în gama

și dreapta d prim Este inclusă

în gama și va rezulta că punctele

a b și c sunt și ele în gama Deci

rezultă că a b și c aparține lui

gama cu ele sunt puncte necoliniare

Deci așa mai departe va rezultat

că de fapt planul gama egal cu

planul determinat de punctele abc

Deci va rezulta din această relație

și din aceasta că planul gama este

egal cu planul alfa și de aici

unicitatea acestui plan Montăm

că planul alfa a se poate scrie

astfel avem un plan determinat

de două drepte d și d prim Deci

folosind notația pe care am folosit

o și la drepte concurente