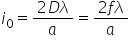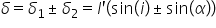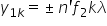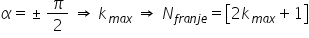Difracţia luminii. Franje în reţele de difracţie.

încet da Șase lecții de optică

ondulatorie vom discuta despre

fenomenul de difracție a luminii

și despre rețelele de difracție

difractia luminii constă în ocolirea

obstacolelor deci abaterea de la

propagarea pur rectilinie a luminii

fiind în consecință un fenomen

ondulator în difracție la baza

căreia stă principiul cui gen frontul

de undă se deformează la întâlnirea

unui obstacol sau orificiu și lumina

se propagă în spatele acestui adică

în zona de umbră în care pe baza

pur geometrice adică de propagare

rectilinie lumina nu ar trebui

să ajung unde de tractat a interfera

asta înseamnă că Distracția e însoțită

de France luminoase și întunecate

și că unele frangi o ar fi colorate

Acest lucru se poate vedea în această

imagine în care vedem Distracția

razelor soarelui aflat la apus

printre copaci în care vedem În

primul rând faptul că între adevăr

lumina ajunge în zona de umbră

în care pe baza Pure geometrice

rect de propagare rectilinie nu

ar trebui să ajungă de asemeni

putem vedea că razele defectate

prezintă aceste fraze în diferite

culori putem identifica varii culori

în lumina de tractat cele doua

imagine prezintă același lucru

Dar pentru razele ce vin de la

lună Evident prin reflexie sunt

raze provenită de la soare dar

reflectate pe lună difracția razelor

lunii printre norii sfera pământului

poate fi văzut în această imagine

și din nou putem vedea formarea

unor frunze colorate experimental

Se pot observa franjele obținută

din difracție Spre exemplu dacă

pornim cu un dispozitiv Young și

blocăm una dintre cele două surse

deci pur și simplu punem un o placă

care nu permite trecerea luminii

ucla copac în pe surse a doua ceea

ce se observă în acest caz este

că franjele de interferență nu

dispară deci franjele de interferență

Ale dispozitivul lui Young care

nu mai este dispozitiv Young odată

ce blocăm sursa doi nu dispar în

continuare obținem fraze de interferență

dar proprietățile lor se schimb

mai exact franja centrală care

in dispozitivul Young este centrată

în jurul axului de simetrie se

mută în fața funde libere Deci

franja centrală de intensitate

maximă se mută în dreptul sursei

reci obținem o flanșă mare aici

și apoi vom obține o serie de fraze

de intensitate mai mică de asemenea

această franjuri centrală de vine

Alba și dominantă adică raportul

dintre intensitatea frangi centrale

luminoase și franjele centrale

secundare luminoase crești un alt

tip de experiment simplu Ce se

poate face Pentru observarea de

fracții este dacă se va Aza dimensiunea

chestie Fendt Deci dispozitivul

de Vine cel din cele al doilea

de centura a doua schemă s1d vine

el să avem o singură fată dar folosim

o fantă cu dimensiune mare în care

de dimensiunea a este mult mai

mare decât lungimea de undă a sursei

monocromatice ce generează un da

luminoasă inițial în acest caz

numai obținem cod de fracții numai

obținem fraze de interferență sau

de difracție și pur și simplu o

zonă luminoasă o pată luminoasă

pe ecran Dacă micșorăm dimensiunea

aceste fente până când ia devine

comparabilă cu lungimea de undă

a radiației luminoase monocromatice

obținem aceste fraze de difracție

de tipul celor care în desenat

În consecință distracție apare

la trecerea prin orificii sau prin

obstacole ale căror dimensiuni

sunt comparabile cu lungimea de

undă a luminii Haideți să discutăm

despre franjele de difracție Deci

avem un dispozitiv experimental

care schematică este prezentat

în această imagine în care avem

o singură frază de dimensiunea

ei pe mărimea am și un ecran aflat

la o distanță de și un punct p

oarecare gaseste clan dacă a este

după cum am spus comparabil cu

lungimea de undă Lambda a sursei

de lumină monocromatică atunci

vom obține frangem de distracție

pe ecran ele vor arăta precum cele

din această imagine Deci vom obține

o flanșă centrală luminoasă de

intensitate mai mare albă de culoare

albă centrată în poziția 0 în poziția

euro Deci poziția centrala ecranului

încerce ăsta este zero și apoi

vom obține frangi colorate de intensitate

mai mică și de lărgime mai mică

Pe măsură ce ne departe de centrul

ecranului intensitatea ca funcție

de Ioan de este poziția dea lungul

ecranului arată ceva de genul acesta

Deci avem o flanșă centrală luminoasă

mare și apoi verificați din ce

în ce mai mici avem o distribuție

simetrică a franjuri față de poziția

central Deci aceasta este intensitatea

luminoasă a frazelor de difracție

ca funcție de poziția y de a lungul

ecranului Haideți să calculăm mărimea

acestei fraze centrale Deci dorim

să calculăm acest parametru notat

cu zero adică distanța dintre primele

fraze întunecate si încadrează

franja centrală de distracții conform

principiului weekend din fracția

apare datorită faptului că fenta

în momentul în care frontul de

undă de la sursa noastră originală

întâlnește Fanta această fată de

Vine cu o colecție de surse secundare

de unde sferice care se propagă

coughend sferice și interfere între

ele aceste Unde în surse secundare

acestei unde secundare sunt coerente

pentru că provin de la aceeași

sursă Deci au aceeași frecvență

și de sunt coerente și pot genera

o interferență staționar acesta

este motivul principal pentru care

în difracție obținem frangi un

fenomen specific interferenței

staționare aceasta este sursa franjuri

lor și anume sursele secundare

coerentei de a lungul fente considerăm

un număr par de astfel de surse

curent veți vedea imediat De ce

Par Deci un număr 2k mărimea unei

surse în concluzie fiind a mărimea

fente împărțită la numărul lor

2k să calculăm diferența de drum

opti cum am făcut întotdeauna a

două surse consecutive Deci r2

ca minus r2 ca minus unu până în

punctul are care pe pe ecran Deci

Am mărit această imagine pentru

a vedea geometria acestui fenomen

de difracție Deci avem sus sa cu

numărul 2 comments 1 și sursa consecutivă

următoare s sursa numărul 2k vom

avea două drumuri optice Hair 2k

de la sursa s2k până în p și r

2 ca minus 1 și dorim să calculăm

drumul Optic diferența de drum

Optic Delta dintre cele două drumuri

optice notăm cu alfa unghiul făcut

din centrul fente până în punctul

pe veci acestui unghi este Alfa

și observăm că unghiul care subîntinde

diferența de drum Optic Delta este

total asta deoarece această acest

segment a perpendicular pe normală

prin definiție Iar acest segment

este perpendicular pe dreapta c

Unește punctul p cu centrul fente

deci putem scrie că de asta diferența

de drum Optic este egală cu Delta

a diferența sau dimensiunea aceste

sursei diferența dintre poziția

sursei 2 comments 1 și sursei 2k

și Delta sinus de Alfa Aceasta

este o aproximație despre care

am discutat când am vorbit despre

dispozitivul Young Deci această

ecuație este valabilă pentru unghi

un unghi Alfa foarte mic ea nu

este o egalitate în sensul strict

și o aproximație în acest caz vă

rog să le vizitați derivare ecuațiilor

pentru dispozitivul Young unde

am vorbit exact despre această

ecuație pentru diferența de drumul

Optic și ce implică ea în cazul

Alfa foarte mic sau cum anume se

deduce această ecuație pentru unghi

Alfa foarte mic Deci avem această

ecuație pentru diferența de drum

Optic dintre două surse consecutive

acum după cum am spus dorim să

extragem ecuația pentru poziția

celor două fraze întunecate de

ordinul 1 Deci primelor front unei

cate aceste unde interfere distructiv

și se anulează două câte două în

franjele întunecate de ordinul

1 dacă diferența de drum Optic

este egală cu la PD Haideți să

discutăm în primul rând de ce obținem

interferență distructivă foarte

simplu pentru că dorim să calculăm

poziția primelor franje întunecate

acestor două fraze întunecate Franz

întunecată înseamnă intensitate

i minimă după cum veți se vede

din desen ceea ce implică interferență

distructiv De ce două câte două

pentru că ele pentru a obține o

interferență distructivă pentru

toate sursele din fantele cuplăm

două câte două surse le consecutive

și aplicăm condiția ca el este

interfere distractiv în felul acesta

Cum aveau interferență distructivă

de a lungul întregii fente și acesta

este motivul pentru care am considerat

un număr par de surse ele se cuplează

două câte două Și interfera distructiv

în total obținând o condiția pentru

o interferență totală distructivă

în aceste două puncte și dorim

franjuri întunecate de ordinul

1 pentru că dorim să stabilim poziția

acestor fraze intunecate primelor

franjele cat se dă la stânga și

cea de la dreapta franzj a centrale

iar condiția de Franz întunecată

este ca diferența de drum Optic

să fie un multiplu impar de semi

dorind să obținem primele frangi

întunecate punem ca egal cu 0 Deci

Delta diferența de drum Opticris

filanda pe 2 pentru aceste fraze

întunecat în concluzie Delta Care

este a împărțit la 2 k a împărțit

la 2 ca sinus de Alfa trebuie să

fie calculam da pe doi pentru aceste

două franci adică a sinus de Alfa

este egal cu capul unde Venus din

această ecuație putem acum extrage

poziția y1a frazelor de întunecate

de ordinul 1 dec Grecu nu este

plus igrec 1 este poziția frazei

întunecate la dreapta și minus

cu nu poziția franjuri inecate

la stânga în primul rând sinus

de Alfa din acest în această diagramă

sinus de Alfa în acest caz va fi

y1 împărțit la d y 1 având un semn

plus și minus în funcție dacă suntem

de la dreapta sau la stânga punctului

0 de sinus de Alfa este egal cu

plus minus egal cu 1 împărțit la

d și în această ecuație este egal

cu Lambda împărțit la ei din nou

pentru franja tune casă de ordinul

1 în concluzie y 0 care este egal

cu doi unu zero Ed această distanță

cu unu plus unu fiind poziția franjele

cat la dreapta și mie nu se conduce

la stânga d50 va fi 2y cu nu Deci

e 0 pardon de 0 care este mărimea

frazei întunecate centrale vafi

2y cu nu și va fi 2 de la am de

împărțit la de multe ori în experimentele

de difracție se pune o lentilă

convergentă în fața fente și ecranul

atunci bineînțeles se va plasa

în planul focal obiect al acestei

lentile convergente A deci D devine

egal cu F distanța focală a acestei

lentile convergente aceasta pentru

a obține un vizualizare mai bună

a frazelor de difracție atunci

mărimea frazei centrale este egal

cu 2 la împărțit la ei pentru că

de este egal cu ea să discutăm

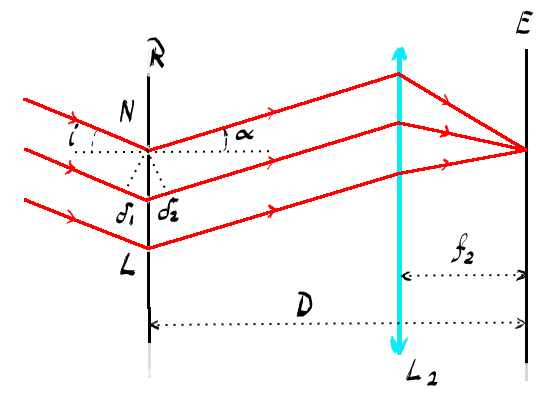
acum despre rețelele de difracție

Deci avem exact același tip de

dispozitiv dar în loc de o fantă

avem un număr mai mare decât unul

de fond ten și vom avea un ecran

la o distanță de și vom folosi

de asemeni două lentile convergente

l1 și L2 una în spate rețele de

distracție și una în față rețele

de fracție un discuta imediat De

ce și cum deci franjele sunt produse

atât de interferența Între fante

cât și de difracția din fiecare

fantă Deci fiecare fantă va avea

un anumit număr de surse secundare

și aceasta va produce în dreptul

ei o figură de difracție o flanșă

de o serie de fraze de difracție

în fața fiecărei fante dar de asemeni

având mai multe fante lumina ce

trece prin fiecare fantă va interfera

cu lumina din celelalte fante ceea

ce este interferența Deci vom avea

de fapt franjele de interferență

pe ecran pe acest ekran modulate

cu franjele de difracție amândouă

fenomene sunt prezente simultan

bineînțeles trebuie să avem un

condiția ca mărimea fiecărei fente

să fie comparabilă cu lungimea

de undă asa se monocromatice se

introduce așa numita constantă

a rețelei care are infante care

este prin definiție lungimea rețele

de difracție împărțită la numărul

de fete se introduce de asemeni

numărul de pe unitatea de lungime

Care este inversul Constantin rețele

el Primo se așează prima lentilă

în planul focal el sau se așează

sursa monocromatică Mai bine spus

în planul focal al primei lentile

convergente a ceea ce înseamnă

că razele de lumină ce cad pe rețeaua

de difracție vor fi paralele de

asemeni se așează lentila convergență

a doua în planul focal astfel încât

Ecranul să fie planul A focal deci

acesta este punctul focal obiect

sau focarul obiect al lentilei

L2 Iar s este focarul imagine al

lentilei l1 și atunci obținem aceste

raze paralele atât la intrarea

în rețeaua de distracție cât și

la ieșire diferența de drum Optic

între undele dintre două fante

consecutive va fi egală cu suma

dintre Delta 1 și de Deci vedeți

diferența de drum între această

rază ce pleacă din s și ajunge

la pe și această rază ce pleacă

tot din a se ajunge la p este egală

cu Delta 1 plus Delta 2 apare de

asemeni un minus pentru cazul în

care considerăm un punct pe de

cealaltă parte a axului dispozitivului

caz în care unde le paralele vor

fi de cealaltă parte a normalei

Deci în acest caz pentru a ajunge

în acest punct p prim să spunem

trebuie să Considerăm unde paralele

ce pleacă de rețeaua de distracție

în sens opus și atunci Delta 2

va avea un sens negativ adică Delta

2 va fi acest Delta 2 și vom avea

diferența de drum Optic Delta 1

minus Delta 2 în acel caz și ea

va fi această diferență de drumul

Optic va fi pur și simplu egală

cu el prin înmulțită cu sinus de

e plus sinus de Alfa unghiul de

intrare și unul de ieșire din rețeaua

de difracție în cazul unui punct

pe aflat pe aceeași parte cu sursa

sau minus în cazul punctului Pepe

aceasta este diferența de drum

Optic a unei rețele de difracție

în care bineînțeles punem condiția

2k Lambda pe 2 pentru a obține

frangi luminoase și Doica plus

1 Landa pe 2 pentru a obține frangi

întunecate Deci vom obține bineînțeles

o frază centrală ca de obicei care

are o intensitate maximă și este

albă și apoi vom obține și flanșe

de ordin superior cum mai mare

decât 0 1 2 3 și așa mai departe

crescător corespunzătoare unui

unghi Alfa crescător aceste franje

de ordin superior raju luminoase

vor avea intensitate descrescătoare

și vor fi colorate pentru că lungimea

lor de unda Lambda va crește împreună

cu ca și Deci o lungime de unda

crescătoare înseamnă o anumită

culoare în spectrul vizibil după

cum am discutat pentru cazul particular

al unei incidență normale Adică

s este pe sursa sa este pe axul

de simetrie al dispozitivului și

atunci razele ce ies din lentila

convergente l1 vor fi paralele

cu Axa acesta axe de simetrie și

Deci voi avea o incidență normală

pe rețeaua de difracție opt avem

e egal cu 0 acest unghi de incidență

și deci diferența de drum Optic

de vine el prin sinus de Alfa egal

cu plus minus calendar pentru franjele

luminoase poziția primului primului

primei fraze y1 pentru ca egal

cu unu este egală cu f2f doi fiind

distanța focală a celei de a doua

lentile Deci acest egal cu 1 este

egal cu F2 tangent de elf în concluzie

putem scrie că y1 este aproximativ

egal cu m prim F2 calanda Deci

y1 este egal cu F2 tangent de Alfa

Dar pentru unghiul Alfa mici acesta

este F2 Alfa Deci Haideți să scriu

undeva y1 este aproximativ egal

cu F2 Alfa dar Alfa din prima ecuație

este egal cu plus minus calanda

supra el prin Deci plus minus f

prim F 2 scuzați F2 halam da împărțit

la el prin dar 1 pe el prime este

egal cu n prim din această definiție

și Deci aceasta este poziția primelor

va francilor de ordinul întâi numărul

total de fraze din textul de difracție

este partea întreagă a acestui

număr Deci luăm doi ca maxim plus

unu unu este franja centrală și

avem apoi un anumit număr ca maxim

de frangi la stânga și la dreapta

de aceea nu doi își 2 ori ca maxim

plus 1 unde ca maxim corespunde

ordinului frangi de difracție pentru

nunți de 90 de grade acesta este

unghiul Alfa Max