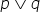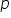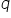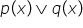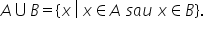Disjuncția propozițiilor și a predicatelor. Reuniunea mulțimilor

Salut Ce mai faceți Mă bucur că

sunteți bine dacă vă mai amintiți

în lecția trecută am început să

discutăm despre operații binare

iar în această lecție o să discutăm

despre o altă operație disjuncția

propozițiilor și a predicatelor

și despre Reuniunea mulțimilor

Fiind date două propoziții pe și

q disjuncția acestora se notează

astfel citim pe sau Q și Aceasta

este o propoziție adevărată dacă

și numai dacă cel puțin una dintre

propozițiile P sau q este adevărată

avem alăturat și tabelul de valori

Observați că este suficient ca

una dintre cele două propoziții

să fie adevărată pentru ca disjuncția

acestora să fie o propoziția adevărată

să vedem un exemplu avem propoziția

pe 3 plus 4 egal cu 10 Aceasta

este o propozitie falsă Deci valoarea

de adevăr a propoziției pe e este

0 propoziția q 27 este divizibil

cu 3 Aceasta este o propozitie

adevărată atunci disjuncția acestor

propoziții se citește astfel 3

plus 4 este egal cu 10 sau 27 este

divizibil cu 3 valoarea de adevăr

a propoziției pe sau q este egală

cu unu de ce este mai mic decât

3 este o propoziție falsă 8 este

multiplu de 5 este o propoziție

falsă prin urmare valoarea de adevăr

a propoziției pe sau fiul este

egală cu 0 pentru că nici una din

cele două propoziții este adevărată

șase este număr natural avem o

propoziție adevărată 4 plus 6 este

egal cu 10 este de asemenea o propoziție

adevărată atunci valoarea de adevăr

a propoziției pe sau cum va fi

1 discutăm în continuare despre

disjuncție a predicatelor Fiind

date două predicate pe de x și

q de x disjuncția acestora se notează

astfel și citim p de x sau Q de

x facem un exemplu avem predicatul

p de x x mai mic sau egal decât

4 unde x este număr natural q de

x x divide pe 5 unde x este număr

natural atunci predicatul p de

x sau qdx se Formulează astfel

x este mai mic sau egal decât 4

sau x divide pe 5 unde x este număr

natural această propoziție este

adevărată pentru acele valori ale

lui x pentru care cel puțin una

dintre propozițiile de mai sus

este adevărată și falsă în celelalte

cazuri să vedem în continuare care

sunt mulțimile de adevăr ale acestui

predicate mulțimea de adevăr a

predicatului p este formată din

numerele naturale mai mici sau

egale cu patru acestea sunt 0 1

2 3 și 4 mulțimea de adevăr a predicatului

q este formată din divizorii naturali

ai numărului cinci Aceștia sunt

unu și cinci și acum se scrie mulțimea

de adevăr a disjuncția acestor

predicate x poate să fie un element

din prima mulțime sau din a doua

mulțime și atunci mulțimea de adevăr

adjuncții a este formată din elementele

0 1 2 3 4 sau 5 pe 1 No să nu mai

scriem pentru că deja o dată însă

această mulțime reprezintă Reuniunea

celor două mulțimi scrise mai sus

și atunci Putem să scriem această

formulăm mulțimea de adevăr a predicatului

p de x sau Q de x este formată

din mulțimea de adevăr a predicatului

p reunită cu mulțimea de adevăr

a predicatului q Reuniunea a doua

mulțimi se definește prin produs

funcție aceasta este mulțimea elementelor

x cu proprietatea că x aparține

lui a sau x aparține lui b dacă

Privim această diagramă atunci

Reuniunea celor două mulțimi este

formată din această suprafață hașurată

în continuare o să facem niște

aplicații Se dau următoarele propoziții

propoziția pe oricare ar fi x număr

real x la a doua minus 9 este diferit

de zero propoziția q există x număr

natural astfel încât 3x minus 12

să fie mai mare sau egal decât

0 se cere să stabilim valoarea

de adevăr a propozițiilor p q n

p q p q p sau non Q N P sau Q N

P sau non q mai întâi O să stabilim

valoarea de adevăr a propoziției

pe trebuie să verificăm dacă pentru

orice x număr real are loc această

relație x la a doua minus 9 să

fie diferit de 0 însă dacă x este

egal cu 3 observăm că x la a doua

minus 9 este egal cu 9 minus 9

și egal cu 0 la fel se întâmplă

și dacă x este minus 3 prin urmare

această relație nu are loc pentru

orice x număr real Așadar propoziția

universală este falsă pentru propoziția

q trebuie să verificăm dacă există

cel puțin un număr natural x astfel

încât 3x minus 12 să fie mai mare

sau egal decât 0 Bineînțeles că

există un astfel de număr Chiar

și mai multe dacă x este 5 avem

trei ori 5 minus 12 mai mare sau

egal decât 0 pentru că 3 este mai

mare sau egal decât 0 prin urmare

având în vedere că există cel puțin

un x număr natural pentru care

are loc această inegalitate putem

spune că propoziția existențială

este o propoziție adevărată și

atunci Haideți să scriem aici mai

jos că valoarea de adevăr a propoziției

pe este 0 valoarea de adevăr a

propoziției q este 1 valoarea de

adevăr a propoziției non pe este

1 reamintească negația unei propoziții

pe este falsă dacă pe este adevărată

și invers este adevărată dacă este

falsă valoarea de adevăr a propoziției

nu nicku este 0 deoarece propoziția

q este adevărată de chinon q este

falsă valoarea de adevăr a propoziției

pe sau Q din moment ce avem cel

puțin una dintre cele două propoziții

adevărată înseamnă că disjuncția

acestora este propoziție adevărată

valoarea de adevăr a propoziției

P sau non q pe este falsă nu în

q este falsă Deci avem două propoziții

false în acest caz disjuncția lor

este o propoziție falsă valoarea

de adevăr a propoziției non P sau

Q Deci aici trebuie să negăm disjuncția

propozițiilor P sau Q era o propoziție

adevărată negația acesteia este

propoziție falsă și valoarea de

adevăr a propoziției non P sau

nu în Q nunta este adevărată nu

unchiul este falsă avem cel puțin

o propoziție adevărată prin urmare

disjuncția acestora este o propoziție

adevărată și mai facem un ultim

exercițiu cu predicate pe mulțimea

M formată din elementele 2 3 4

5 6 7 și 8 avem următoarele două

predicate predicatul p de x x este

divizor al lui 12 și predicatul

q x este pătrat perfect se cere

să determinăm mulțimea de adevăr

a predicatului p mulțimea de adevăr

a predicatului q și mulțimea de

adevăr a disjuncția a celor două

predicate pentru a scrie mulțimea

de adevăr a predicatului p trebuie

să ne uităm la această mulțime

m și să vedem Care dintre aceste

numere sunt și divizori ai numărului

12 pinul mare avem elementele 2

3 patru și șase Aceștia sunt toți

divizorii numărului 12 din mulțimea

M trecem la mulțimea de adevăr

a predicatului q trebuie să scriem

toate pătratele perfecte din mulțimea

M observăm că avem un singur pătrat

perfect și acesta este 4 mulțimea

de adevăr a predicatului P sau

q este formată din Reuniunea celor

două mulțimi filmarea avem elementele

2 3 4 și 6