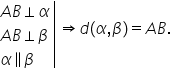Distanţe în spațiu. Perpendiculare și oblice.

în această secvență vom vedea Ce

înțelegem prin distanță în spațiu

și vom vorbi puțin și despre perpendiculare

Și oblice În ce situații mi se

poate cere să calculăm niște distanțe

Păi putem să avem distanța dintre

două puncte iar distanța dintre

punctele a și b e dată de fapt

de lungimea segmentului AB distanța

dintre două puncte lungimea segmentului

determinat de cele două puncte

și notăm astfel distanța dintre

punctele a și b este egală cu lungimea

segmentului AB și dacă trecem aici

că ab are 2 cm atunci trecem în

continuare egal cu 2 cm sau putem

să avem distanța dintre un punct

și o dreaptă Păi ca să găsim distanța

de la punctul A la dreapta a mic

Trebuie să ducem perpendiculara

din punctul A pe dreapta a mic

și atunci notăm aici punctul b

mare AB este perpendiculară pe

dreapta a mic atunci asta înseamnă

că distanța de la punctul A la

dreapta a este dată chiar de lungimea

segmentului AB și dacă trecem că

avem aici și 1 cm atunci notăm aici

1 cm mare atenție perpendiculara

dusă din punct Pe o dreaptă este

unică Deci din punctul A mare pe

dreapta a mic putem să ducem o

singură perpendiculară în afară

de aceste două tipuri de distanțe

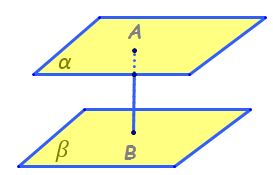
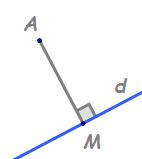
mai putem să avem distanța de la

un punct la un plan Deci dacă vrem

să determinăm distanța de la punctul

A mare la planul alfa pungi tu

cm perpendiculara din punctul A

pe planul alfa și dacă această

perpendiculară intersectează planul

în punctul o Haide să trecem pe

o aici și să prelungim și această

dreaptă atunci vom nota că de vreme

ce a o este perpendiculară pe planul

alfa înseamnă că distanța de la

punctul A la planul de la punctul

A la planul alfa este dată chiar

de lungimea segmentului AO 10 egal

cu AO și trecem apoi în continuare

Câți centimetri are acest segment

atenție perpendiculara dusă dintre

un punct pe un plan ca și perpendiculară

dusă de la un punct Pe o dreaptă

este unică Deci din punctul A pe

planul alfa putem să ducem o singură

perpendiculară AO este unică dacă

unim punctul cu orice alt punct

din plan de exemplu dacă avem aici

punctul b și unim punctul A cu

punctul b sau avem aici punctul

c și unim pe a cu c atunci ceea

ce vom obține ab și ac se numesc

oblice la plug și ac sunt oblice

la planul alfa ce relație credeți

că există între OB cele la un plan

și distanța de la punctul respectiv

la plata Păi întotdeauna orice

oblică la plan este mai lungă decât

perpendiculară pe acel plan de

ce se întâmplă acest lucru Iată

dacă unim aici pe b cu o avem triunghiul

AOB Ce fel de triunghi este acesta

cum a o e perpendiculară pe planul

alfa și 8 d este inclusă în planul

seamănă ca o a perpendiculară pe

OB de ce avem aici un unghi de

90 de grade d și triunghiul AOB

este triunghi dreptunghic și ce

observă că ab este ipotenuză iar

AO este catetă pe intotdeauna ipotenuza

este mai lungă decât cateta deci

putem să trecem aici că o oblică

la plan ne referim aici la a b

este mai lungă decât a o adică

perpendiculara dusă din acest punct

Pe plan dintre două oblice la un

plan de exemplu Dacă vom prelungi

aici și acest segment OB și chiar

îl luăm prelungii și Să considerăm

că avem aici punctul de a de a

sta și a oblică la la haideți so

trasăm a bun dintre două oblice

la un plan este mai lungă cea care

este mai depărtată de punctul în

care perpendiculară intersectează

planul în cazul nostru față de

punctul O deci cu cât ne depărtăm

mai mult de punctul O cu atât obliga

la plan va fi mai lungă pentru

că Iată aici avem tot așa un triunghi

dreptunghic a o d și devreme c

o d este mai lungă decât o b atunci

și AD va fi mai lungă decât ab

de putem să notăm că de are lungimea

mai mare decât a b de dintre două

oblice la un plan este mai lungă

cea care este mai depărtată de

punctul o în acest caz mai putem

să întâlnim și distanța dintre

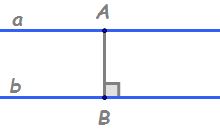
două drepte paralele ca să determinăm

distanța dintre două drepte paralele

alege un punct pe una din cele

două drepte de exemplu alegem aici

punctul m și din punctul M ducem

o perpendiculară pe dreapta b și

să notăm aici cu n punctul de intersecție

m n este perpendiculară pe dreapta

b însă cam dreptele b și a sunt

drepte paralele înseamnă că mn

este cam perpendiculară pe dreapta

A deci trecem aici dreptele a și

b sunt paralele m n este perpendiculară

pe dreapta m n este perpendiculară

și pe dreapta b atunci distanța

de la dreptele distanța dintre

dreptele a și b e dată chiar de

lungimea segmentului m n dacă avem

aici să spunem un centimetru atunci

trecem în continuare egal cu 1

cm sau mai putem să avem distanța

dintre două plane paralele ca să

determinăm o asemenea distanță

vom proceda asemănător cu ce am

făcut aici și anume alegem un punct

e în acest plan de să se înțeleagă

că avem aici e din punctul E coborâm

o perpendiculară pe planul Beta

și Haideți Să considerăm că intersectează

aici în punctul f Deci e f este

perpendiculară pe planul Beta Cum

însă planele Alfa și Beta sunt

paralele înseamnă că e f este perpendiculară

și pe planul alfa Deci f perpendiculară

și pe Alfa pentru că planele Alfa

și Beta sunt plane paralele și

atunci distanța de la plan dintre

planele Alfa și Beta e dată chiar

de lungimea segmentului cuprins

între aceste două plane așa cum

am avut aici lungimea segmentului

cuprins între aceste două drepte

De ce este dată de lungimea segmentului

ef ne dacă e fare să spunem 3 cm

atunci trecem în continuare egal

cu 3 cm să facem acum și această

aplicație Se dă un cub cu lungimea

muchiei de 2 cm să aflăm distanța

dintre planele a b c d de cea Ce

plan și planul a prim b prim c

prim D prim adică acest plan cum

determinăm distanța dintre cele

două plane Păi avem aici un cub

asta înseamnă că planul a b c d

este paralel cu planul a prim b

prim c prim D prim dacă vreți chiar

Să demonstrăm acest lucru atunci

e foarte simplu pentru că Fețele

unui cub absolut toate fețele sunt

pătrate pe asta înseamnă că b d

prim este perpendiculară pe BC

la fel B B prim este perpendiculară

și pe AB Deci B B prim a perpendiculară

pe două drepte concurente din planul

ABCD asta înseamnă că b d prim

a perpendiculară pe acest plan

test trecem B B prim e perpendicular

Pe planul ABCD AB Salut la fel

se demonstrează că b d prim e perpendiculară

pe planul a prim b prim c prim

D prim BB prim perpendicular pe

AC plan cu alte cuvinte cele două

plane a b c d și a prim b prim

c prim D prim sunt plane paralele

Deci rezultă că distanța dintre

aceste două plane Haide să scriu

mai la stânga pentru că nu o să

ne încadrăm în spațiu Deci distanța

dintre planele a b c d și a prim

b prim c prim D prim este dată

de fapt de lungimea segmentului

cuprins între aceste plane 10 egal

cu lungimea segmentului B B prim

par Evident este congruent cu c

c prim cu d d prim și cu a aprinde

și puteam să alegem în loc de bebe

prin orice alte muchie dintre acestea

4 și cât avem lungimea muchiei

este de 2 cm Deci distanța dintre

aceste două plane este de 2 cm

o altă aplicație Pe planul triunghiului

ABC isoscel ab egal ac egal 15

cm și BC de 18 cm se ridică perpendiculara

m a Fie d mijlocul segmentului

BC și mi se mai spune aici că dacă

e m de l 20 de cm să aflăm această

distanță deci mai întâi trebuie

să desenăm planul triunghiului

ABC avem un triunghi isoscel care

are AB egal cu AC 15 cm și aici

avem 18 cm Lungimea segmentului

BC și se ridică perpendiculara

m a Deci ridicăm aici însă nu am

trecut corect nu am trasat corect

avem aici ma perpendiculară pe

planul abc chiar o să și le notez

că m a este perpendiculară pe planul

abc Fie d mijlocul segmentului

b c d și trecem aici d mijlocul

segmentului BC Deci BD congruent

cu dc și mi se spune că dacă md

are 20 de centimetri să unim pe

m cu d Deci dacă lungimea acestui

segment este de 20 de cm să aflăm

distanța de la punctul M la planul

abc Ce înțelegem prin această distanță

e de vreme ce ma este perpendiculară

pe planul abc atunci distanța de

la punctul M la aceste plane dată

chiar de lungimea segmentului ma

Deci din această relație rezultă

că distanța de la punctul M la

planul a b c este dată de lungime

a acestui segment Ema cu alte cuvinte

trebuie să vedem Câți centimetri

are segmentul Emma Cum să calculăm

lungimea acestui segment Păi nu

degeaba mi sa dat lungimea segmentului

m d Iată dacă unim pe a cu d vom

obține triunghiul m a d Ce fel

de triunghi este acesta pe cum.ma

este perpendiculară pe planul ABC

și AD e Face parte din acest plan

înseamnă că m a este perpendiculară

pe a d Deci avem aici un unghi

de 90 de grade cu alte cuvinte

triunghiul m a d este un triunghi

dreptunghic știind lungimea ipotenuzei

ca să aflăm lungimea acestei catete

avem nevoie de lungimea catetei

ad și atunci cum să determinăm

lungimea segmentului ad Păi ce

este AD este mediană în triunghiul

ABC Care este triunghi isoscel

cu alte cuvinte Problema e deja

rezolvată pentru că știm lungimile

laturilor și Ce este atunci a d

de vreme ce e mediană în triunghi

isoscel dar este și înălțime Deci

trece maici că avem înălțime Haide

să notăm că triunghiul ABC este

un triunghi isoscel iar a d este

mediană corespunzătoare bazei acesteia

triunghi isoscel d c rezultă că

AD este și înălțime ad perpendiculară

pe BC cu alte cuvinte notăm că

măsura unghiului adb este de 90

de grade Deci ce am obținut din

această relație că triunghiul d

c rezultă în continuare că triunghiul

adb este un triunghi dreptunghic

măsura unghiului d are 90 de grade

și atunci aplicăm aici teorema

lui Pitagora pentru că Iată BD

are 9 cm voi face aici o acoladă

și scrie 9cm Deci rezultă din teorema

lui Pitagora că a de la pătrat

este egală cu a lungimea acestui

segment este egală cu diferența

dintre a b pătrat care lungimea

ipotenuzei și BD la pătrat Deci

ei de pătrat cât ne dă Avem așa

a b pătrat 15 la pătrat minus b

de la pătrat înseamnă 9 la a doua

Dică două sute 25 minus 81 ne dă

144 10 rezultă că a d are 12 cm

și venim aici și trecem 12 cm un

deja Problema e ca și rezolvată

venim aici și notăm că a este perpendiculară

pe planul abc trebuie să justificăm

faptul că triunghiul mnd este un

triunghi dreptunghic în A deci

ma e perpendiculară pe acest plan

a d este inclusă în planul ABC

de unde rezultă că m a este perpendiculară

pe a d Deci notăm că măsura unghiului

Cum se numește ma d are 90 de grade

și atunci aplicăm teorema lui Pitagora

în unghiul m a d Deci avem așa

triunghiul m a d măsura unghiului

A iar aici are 90 de grade Deci

vom avea conform teoremei lui Pitagora

pătratul lungimii a catetei a m

sau Ema la pătrat va fi egală cu

MD la pătrat din care scădem a

de la pătrat și să înlocuim rezultă

că m a la pătrat va fi egală cu

MD este de 20 de cm la pătrat minus

Deci aici avem la a doua a de la

pătrat ne dă ad12 Deci Avem 12

la a doua și obținem 400 minus

144 Deci ne dă Deci 6 rezultă că

lungimea catetei m a este radical

din 256 adică 16 cm și venim aici

ștergem semnul întrebării și trecem

că am obținut 16 cm și astfel am

aflat distanța de la punctul M

la planul abc
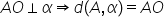
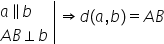