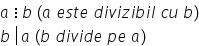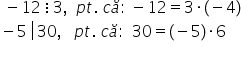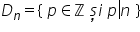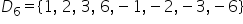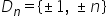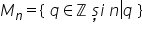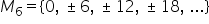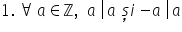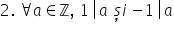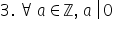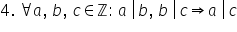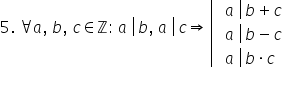Divizibilitatea numerelor întregi

divizibilitatea numerelor întregi

avem următoarea definiție numărul

întreg a este divizibil cu numărul

întreg b dacă există un număr întreg

c astfel încât a egal cu b ori

c relația de divizibilitate se

poate înota în două moduri a este

divizibil cu b sau b divide pe

a de exemplu numărul minus 12 este

divizibil cu numărul 3 deoarece

minus 12 se poate scrie trei ori

minus patru sau nu mai putem Scrie

3 divide numărul minus 12 numerele

3 și minus 4 se numesc divizori

ai numărului minus 12 iar minus

12 se numește multiplu al numerelor

3 și minus 4 să vedem Ce înțelegem

prin mulțimea divizorilor unui

număr dacă avem n un număr întreg

mulțimea divizorilor lui N se notează

cu d indice n ce este formată din

acele numere întregi pe cu proprietatea

că p divide pe end Dacă n este

un număr prim atunci mulțimea divizorilor

lui N conține exact patru elemente

și anume plus minus 1 și plus minus

n de exemplu mulțimea divizorilor

numărului prim 5 va fi formată

din următoarele elemente 1 5 minus

1 și minus 5 mulțimea multiplilor

numărului n se notează cu m indice

n și este formată din numerele

întregi q cu proprietatea că n

divide pe q să vedem în continuare

câteva proprietăți ale relației

de divizibilitate prima proprietate

Oricare ar fi a un număr întreg

a divide pe a și minus A divide

pe a 2-a proprietate Oricare ar

fi a un număr întreg unu și minus

unu sunt divizori ai numărului

a 3-a proprietate 0 este divizibil

cu orice număr întreg a patra proprietate

Fie a b și c trei numere întregi

dacă b divide pe a și c divide

pe b atunci c divide pe a această

proprietate se mai numește și tranzitivitatea

relației de divizibilitate și ultima

proprietate dacă b divide pe A

și B divide pe c Atunci b divide

suma a plus apoi D divide și diferența

a minus c și de asemenea b divide

produsul dintre a și c Păi demonstra

ultimele două proprietăți încep

cu proprietatea numărul 4 Știind

că b divide pe a și c divide pe

b și vrem să demonstrăm că c divide

pe a nefolosit definiția dacă b

divide pe A atunci rezultă că a

se va scrie b ori un număr oarecare

k din a doua relație rezultă că

dacă c divide pe b de se scrie

si un număr oarecare pe la aceste

două relații obținem că a va fi

egal cu în loc de B scrie m c ori

pe ori k dar știind că înmulțirea

este asociativă și atunci Putem

să scriem ce ori pe ori k având

în vedere că ei se scrie ca un

produs de doi factori dintre care

unul din ei este Si atunci Cu siguranță

ce divide numărul a și a cincea

proprietate Știind că b divide

pe A și B divide pe c și vrem să

demonstrăm că b divide suma diferența

și produsul numerelor a și c folosim

din nou definiția dacă b divide

pe a rezultă că a se va scrie b

ori un număr k iar din a doua relație

rezultă că ce se poate scrie b

ori un alt număr pe și acum să

facem suma dintre a și c a plus

c va fi egal cu b ori k a plus

b ori pe putem da factor comun

pe b și obținem de pe lângă k plus

pe f având în vedere că a plus

c se scrie ca un produs de doi

factori dintre care unul este b

va rezulta că b divide a plus c

Mami nu știu ce va fi egal cu b

ori k minus b ori pe putem da factor

comun pe b egal cu 2 pe lângă k

minus pe observăm că a minus ce

se scrie ca un produs de doi factori

dintre care unul este b și atunci

rezultă că b divide și a minus

c și acum calculăm produsul numerelor

a și c acesta va fi egal cu b ori

k ori b ori pe să ne declar că

unul din factori este b și atunci

putem să tragem concluzia că b

divide și produsul a ori c am demonstrat

Așadar și această proprietate a

acestei au fost cele mai importante

proprietăți ale relației de divizibilitate

în continuare o să facem două exerciții

primul exercițiu Calculați mulțimea

divizorilor numărului minus 12

intersectată cu mulțimea divizorilor

numărului 18 mai întâi elementele

fiecărei mulțimi apoi vedem intersecția

lor încep cu mulțimea divizorilor

numărului minus 12 aceasta conține

următoarele numere întregi 1 2

3 4 612 și opusele lor A minus

1 minus 2 minus 3 minus 4 minus

6 și minus 12 și acum să vedem

mulțimea divizorilor numărului

18 1 2 3 6 9 18 și opusele lor

minus 1 minus 2 minus 3 minus 6

minus 9 și minus 18 și acum să

calculăm intersecția mulțimea divizorilor

numărului minus 12 intersectată

cu mulțimea divizorilor numărului

18 ne uităm la elementele comune

acestea sunt unu doi 3 6 și minus

1 minus 2 minus 3 și minus 6 aflați

elementele următoarelor mulțimi

mulțimea A formată din acele numere

întregi x cu proprietatea că fracția

7 supra x minus 2 să fie număr

întreg începem întâi cu mulțimea

a apoi o să vedem și cealaltă mulțime

pentru ca fracția 7 supra x minus

2 să fie număr întreg va trebui

ca 7 Să se împartă exact la numitor

sau altfel spus trebuie ca x minus

2 să fie un divizor al numărului

șapte Și atunci vom pune condiția

ca x minus 2 să aparțină mulțimii

divizorilor numărului șapte mulțimea

divizorilor lui 7 va conține următoarele

numere întregi unu șapte minus

unu și minus șapte șapte fiind

număr prim mulțimea divizorilor

lui Șapte va avea exact patru elemente

x minus doi este egală pe rând

cu fiecare din acești divizori

începem cu x minus 2 egal cu unu

mă așa dar patru ecuații de unde

o să aflăm necunoscuta x prima

ecuației este aceasta x minus 2

egal cu 1 astfel aflăm pe x va

trebui să adunăm opusul numărului

minus 2 Așadar adunăm numărul 2

în fiecare membru al ecuației și

obținem x egal 1 plus 2 x b fi

egal cu 3 aceasta ar fi prima variantă

a doua posibilitate este ca x minus

2 să fie egal cu 7 la fel adunăm

numărul 2 în fiecare membru al

ecuației și obținem x egal cu 7

plus 2x egal cu 9 mai departe x

minus 2 egal cu minus 1 adunăm

numărul doi și obținem x egal cu

minus 1 plus 2x egal cu 1 Ciudin

la posibilitate x minus 2 egal

cu minus șapte adunând numărul

2 la ambii membri obținem x egal

cu minus 7 plus 2 x egal cu minus

5 am obținut patru valori pentru

variabilă x și atunci mulțimea

a va fi formată din aceste numere

întregi 3 9 1 și minus 5 îmbinare

3 cm la a doua mulțime mulțimea

b formată din acele numere întregi

x cu proprietatea că 4x plus 5

supra 2x plus 1 trebuie să fie

număr întreg o să mai scriu o dată

această fracție 4 x plus 5 supra

2x plus 1 trebuie să fie număr

întreg Încercăm să facem niște

transformări asupra acestei fracții

astfel încât la numărător să avem

un număr întreg astfel încât să

putem să scriem divizorii acelui

număr și atunci fracția 4 x plus

5 supra 2x plus 1 se poate scrie

4x în locul lui cinci vom scrie

doi plus trei supra 2x plus 1 din

primii doi termeni Da factor comun

pe 2 2 pe lângă 2x plus 1 plus

trei supra 2x plus 1 la numărător

avem o sumă și atunci putem să

despărțim această fracție în două

fracții având același numitor scrie

egal cu 2 pe lângă 2x plus 1 supra

2x plus 1 plus 3 supra 2 x plus

1 prima fracție se poate simplifica

cu 2 x plus unu deoarece apare

atât la numitor cât și la numărător

și obținem a egal cu 2 supra 1

pe care nu mai scriu plus 3 supra

2x plus 1 acesta trebuie să fie

un număr întreg având în vedere

că doi este deja număr întreg mai

punem condiția ca fracția 3 supra

2x plus 1 să fie număr întreg pentru

ca tre să se împartă exact la 2

x plus 1 a trebui ca 2x plus 1

să fie un divizor al numărului

3 și vom scrie atunci 2x plus 1

aparține mulțimii divizorilor numărului

3 mulțimea divizorilor numărului

3 este formată din numerele 1 3

minus unu și minus 3 mă forma Așadar

patru ecuații de unde o să aflăm

necunoscuta x voi continua aici

2x plus 1 egal cu 1 Încercăm să

obținem în membrul stâng necunoscuta

x și să o separăm de ceilalți termeni

ca să eliminăm Numărul 1 din membrul

stâng va trebui să scădem numărul

unu Fiecare membru al ecuației

și avem 2x egal cu 1 minus 1 2x

egal cu 0 de unde x va fi egal

cu zero aceasta este prima variantă

apoi 2x plus 1 egal cu 3 la fel

scădem numărul 1 și avem 2 x egal

cu 3 minus 1 2 x egal cu 2 împărțim

la coeficientul lui x și obținem

x egal cu 2 împărțit la 2 adică

x egal cu 1 aceasta este a doua

posibilitate apoi 2x plus 1 egal

cu minus 1 scădem numărul minus

1 și obținem 2 x egal cu minus

1 minus 1 2 x egal cu minus doi

împărțim la doi x egal cu minus

2 împărțit la 2 x egal cu minus

1 și ultima posibilitate 2x plus

1 să fie egal cu minus 3 scădem

numărul unu din fiecare membru

și obținem 2 x egal cu minus 3

minus 1 2 x egal cu minus 4 împărțit

la 2 x egal cu minus 4 împărțit

la 2 x egal cu minus 2 am obținut

patru valori ale necunoscutei x

și atunci putem să concluzionăm

mulțimea B va fi formată din aceste

numere întregi pe care le am obținut

0 1 minus unu și minus doi