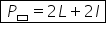Dreptunghiul

în această lecție voi vorbi despre

dreptunghi și proprietățile acestuia

și o să încep cu definiția Paralelogramul

cu un unghi drept se numește dreptunghi

având în vedere că dreptunghiul

este un paralelogram particular

înseamnă că acesta va avea toate

proprietățile paralelogramului

și anume Laturile opuse înfrunt

dreptunghi sunt paralele două câte

două Laturile opuse vor fi și congruente

două câte două unghiurile opuse

sunt congruente iar unghiurile

alăturate sunt suplementare Dacă

măsura unghiului a este de 90 de

grade iar unghiul A este congruent

cu unghiul c fiind unghiuri opuse

înseamnă că și unghiul c la un

unghi drept Dacă unghiurile a și

b sunt suplementare înseamnă că

măsura unghiului Deva fi egală

cu 180 de grade minus 90 de grade

egal cu 90 de grade iar unghiul

b fiind congruent cu unghiul D

va avea și acesta a zburat de 90

de grade constatăm Așadar că toate

unghiurile unui dreptunghi sunt

unghiuri drepte Aceasta este o

consecință a definiției și a Proprietăților

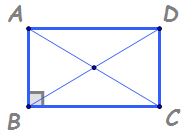
paralelogramului dacă construim

diagonalele observăm că acestea

se înjumătățesc adică punctul de

intersecție al diagonalelor va

fi situat la mijlocul fiecărei

diagonale în plus față de aceste

proprietăți dreptunghiul are o

proprietate specifică și anume

diagonalele unui dreptunghi sunt

congruente Demonstrați Astăzi mă

avem un dreptunghi a b c d și ne

propunem Să arătăm că diagonalele

AC și BD sunt congruente mă folosi

metoda triunghiurilor congruente

o Să arătăm că triunghiurile de

a b și c b a sunt congruente observăm

că acestea sunt triunghiuri dreptunghice

deoarece unghiul A și unghiul b

sunt unghiuri drepte În triunghiul

ab măsura unghiului a este de 90

de grade iar în triunghiul CBA

măsura unghiului b este egală cu

90 de grade Să vedem Ce elemente

congruente au aceste triunghiuri

Dacă a b c d este dreptunghi înseamnă

că laturile opuse sunt congruente

deci a d și b c vor fi congruente

aceste două triunghiuri mai au

o latură comună este vorba de cateta

ab a b este congruent cu a b fiind

o latură comună va rezulta din

cele două relații conform cazului

de congruență catetă catetă că

triunghiul DE ab este congruent

cu triunghiul CBA ia din această

relație de congruență va rezulta

că segmentele AC și BD sunt congruente

este valabilă și reciproca aceste

teoreme un paralelogram care are

diagonalele congruente este dreptunghi

nu o să mai fac demonstrația acestei

teoreme în să rețineți că atunci

când trebuie să arătăm că un paralelogram

este dreptunghi și arătăm că are

un unghi drept și arătăm care diagonalele

congruente să vedem în continuare

Cum putem să calculăm perimetrul

dreptunghiului latura mai lungă

a dreptunghiului se va numi lungime

și se notează cu l mare latura

mai scurtă se va numi lățime și

se notează cu l mic mici observăm

că dreptunghiul are două lungimi

și două lățimi perimetrul oricărui

patrulater în general este suma

lungimilor laturilor de și perimetrul

lui ABCD va fi egal cu ab plus

bc plus CD plus de a dacă înlocuim

aceste laturi cu literele l mare

respectiv l mic vom scrie egal

în continuare cu l mare plus l

mic plus l mare plus l mic știind

că adunarea este comutativă Deci

Putem să schimbăm locul termenilor

din mijloc și voi scrie egal cu

l mare plus l mare plus l mic plus

l mic egal în continuare cu doi

ori al mare plus doi ori al mic

Am obținut o formulă de calcul

pentru perimetrul dreptunghiului

Așadar perimetrul unui dreptunghi

în general este egal cu 2 ori lungimea

plus 2 ori lățimea rețineți această

formulă deoarece se va aplica în

rezolvarea de probleme în continuare

o să facem două aplicații prima

problemă Aflați perimetrul unui

dreptunghi cu lățimea de 20 m și

lungimea egală cu 5 supra 4 din

lățime putem să notăm lățimea 20

m deci el mic va fi egală cu 20

m și lungimea l mare este 5 supra

4 din lățime adică 5 supra 4 ori

al mic egal în continuare cu 5

supra 4 ori 20 putem să simplificăm

pe diagonală cu 4 4 împărțit la

4 este 1 iar 20 împărțit la 4 este

5 5 ori 5 egal cu 25 de m am obținut

lungimea aceasta este egală cu

25 m și acum putem să calculăm

perimetrul dreptunghiului ABCD

formula de calcul este 2 ori lungimea

plus doi ori lățimea egal în continuare

cu doi ori 25 m plus doi ori 20

m egal cu 50 plus 40 egal cu 90

m și următoarea problemă În dreptunghiul

a b c d intersecția diagonalelor

a c și b d este punctul O măsura

unghiului c o b este egală cu 60

de grade Aflați măsurile unghiurilor

triunghiului aob am scris ipoteza

și concluzia trebuie să aflăm mai

exact măsura unghiului AOB măsura

unghiului o a b și măsura unghiului

oba știind că diagonalele unui

dreptunghi sunt congruente și se

înjumătățesc va rezulta atunci

că toate aceste segmente o a o

c o d și o b sunt congruente dacă

oc este egală cu OB înseamnă că

triunghiul c o b este un triunghi

isoscel însă acest triunghi are

și un unghi cu măsura de 60 de

grade Deci în va fi un triunghi

echilateral știind că între un

triunghi echilateral toate unghiurile

au măsura de 60 de grade Deci măsura

unghiului obc va fi egală cu 60

de grade și acum putem să aflăm

măsura unghiului oba Dacă scădem

din 90 de grade cele 60 de grade

și obținem 30 de grade vă reamintesc

că unghiul b adică unghiul abc

este un unghi drept Așadar având

în vedere că a o este egală cu

o c și este egală cu AC supra 2

adică jumătate din lungimea diagonalei

AC iar d o este egal cu OB și egal

cu d b supra 2 iar diagonalele

a c și d b sunt egale A rezultat

din cele trei relații că a o este

egal cu a o c egal cu d o și egal

cu OB rezultat unci că triunghiul

c o b este un triunghi isoscel

dar măsura unghiului c o b este

60 de grade înseamnă că triunghiul

c o b este echilateral înseamnă

că măsura unghiului obc va fi egală

cu 60 de grade înot această relație

cu unu pentru că o să mai folosim

ulterior și acum putem să aflăm

măsura unghiului oba după cum am

spus scădem din măsura unghiului

b măsura unghiului obc măsura unghiului

oba este egală cu măsura unghiului

a b c minus măsura unghiului obc

egal cu 90 de grade minus 60 de

grade egal cu 30 de grade însă

dacă o a este egală cu o b înseamnă

că și triunghiul oab este un triunghi

isoscel având baza ab știind că

între un triunghi isoscel unghiurile

alăturate bazei sunt congruente

Deci măsura unghiului oab a fi

de 30 de grade și acum mai trebuie

să aflăm doar măsura unghiului

a o b și o calculăm din triunghiul

oab Știind că în orice triunghi

suma măsurilor unghiurilor este

egală cu 180 de grade sau altă

variantă ar fi să observăm că Unghiul

aob este adiacent și suplementar

cu unghiul c o b și atunci putem

să scădem din 180 de grade cele

60 de grade și o să obținem că

măsura unghiului AOB va fi egală

cu 120 de grade Deci acestui unghi

are măsura de 120 de grade să scriem

și cele discutate până acum din

relația 1 rezultă că triunghiul

oab este isoscel rezultat că unghiul

o AB este congruent cu unghiul

oba fiind unghiuri alăturate bazei

înseamnă că măsura unghiului oab

este egală cu măsura unghiului

o b a și egală cu 30 de grade și

acum mai trebuie să aflăm măsura

unghiului aob va fi egală cu 180

de grade minus măsura unghiului

c o b pentru că unghiul a o b și

c o b sunt unghiuri suplementare

egal cu 180 de grade minus 60 de

grade egal cu 120 de grade așadar

am aflat cele trei unghiuri Două

dintre acestea au măsura de 30

de grade iar măsura unghiului AOB

este egală cu 120 de grade