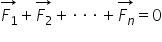Echilibrul de translaţie. Echilibrul punctului material supus la legături.

în prima lecție de statică vom

discuta despre echilibrul de translație

echilibrul de translație a unui

punct material are loc când rezultanta

forțelor ala externe ce acționează

asupra corpului este egală cu zero

punctul material a fost definit

în prima lecție de cinematică și

este practic un corp cu dimensiuni

neglijabile considerăm un punct

material nu pentru că dacă corpul

ar avea dimensiuni atunci această

ecuație egal cu 0 nu are implicau

în echilibru de translație și datorită

faptului că dacă corpul are dimensiuni

pe lângă translație obținem și

alte mișcări mai presus mișcarea

de rotație și dorim să adresăm

separat această acest tip de echilibru

echilibrul de rotație într o lecție

viitoare Deci din nou vorbim despre

puncte materiale pentru a separa

translație de rotație Dacă punctul

are dimensiuni atunci echilibrul

de translație se obține În aceleași

condiții și anume rezultate egale

cu 0 un alt comentariu este că

această ecuație vine direct din

ecuația fundamentală a dinamicii

care era f egal cu m a în cazul

în care această forță este egală

cu zero accelerația este zero ceea

ce înseamnă că corpul este orele

pauză ori mișcare rectilinie uniformă

acesta fiind definiția Unui echilibru

de translație Deci stati ca în

general este un caz particular

al dinamicii Să considerăm un exemplu

simplu Avem două resorturi legate

în serie Deci un prim Resort atașat

de un tavan care apoi întru un

punct A este atașat de un alt Resort

care are la capăt un corp de greutate

G aceasta fiind așa numita legare

în serie a celor două resorturi

cunoaștem constantele K1 și k2

ale celor două resorturi De ce

avem K1 k2 cunoaștem și masă corpului

și știind că întreg sistemul întregul

sistem se află în echilibru de

translație dorim să calculăm în

acest caz a lungimile celor două

resorturi X1 și X2 putem scrie

ecuația pentru echilibru de translație

în punctul C Deci în ce avm acest

echilibru de translație Și de ce

avem că forța elastică F2 resortul

lui 2 plus greutatea corpului acestea

sunt cele două forțe ce acționează

în punctul C este suma lor este

0 alegem o axă de coordonate o

x care este cea verticală și proiectând

această ecuație pe axa o x obținem

că F2 este egală cu gs2 fiind o

forță elastică va fi egal cu Constanta

elastică a resortului 2 înmulțită

cu alungirea lui Care este egal

cu MC rezultă că x 2 este egal

cu m g împărțit la ca 2 de asemeni

punctul a se află în echilibru

de translație pentru că întreg

sistemul se află lichidul translație

deci putem scrie că forțele din

a Care sunt F1 forța elastică a

primului Resort și F2 prin forța

elastică a celui de al doilea Resort

în punctul A au o sumă egală cu

zero unu plus F2 prim este egal

cu 0 proiectând pe axa o x obținem

că F1 este egal cu F2 prin dar

în cazul în care masele celor două

resorturi m-1 și m r 2 sunt mult

mai mici decât masa ma corpului

ceea ce aproape întotdeauna este

cazul avem că F2 prim este egal

cu F2 Dacă resortul 2 are o masă

neglijabilă cele două forțe elastice

de la capetele lui sunt egale asta

pentru că între F2 prime și F2

singura forță posibilă plauzibilă

este greutatea resortului ca și

comentariu dacă nu am avea acest

caz atunci relația să scrie așa

mr2 G masa celui de al doilea Resort

plus F 2 este egal cu F2 prin dar

aproape întotdeauna avem această

situație în concluzie obținem că

F1 este egal cu F2 adică ca 1 x

1 este egal cu ca doi doi șase

obținem ecuația pentru elongație

X1 a primului Resort Care este

ca 2 împărțit la ca unul X2 X2

Evident îl știm din prima ecuație

să trecem la echilibrul de translație

al punctului material supus acțiunii

a trei forțe De ce avem trei forțe

F1 F2 f3 care acționează asupra

unui punct si se află material

Ce se află la intersecția celor

trei forțe echilibrul se va obține

atunci când F1 plus 2 plus f3 suma

vectorială este egală cu 0 după

cum am vorbit această ecuație poate

fi scris în mai multe feluri o

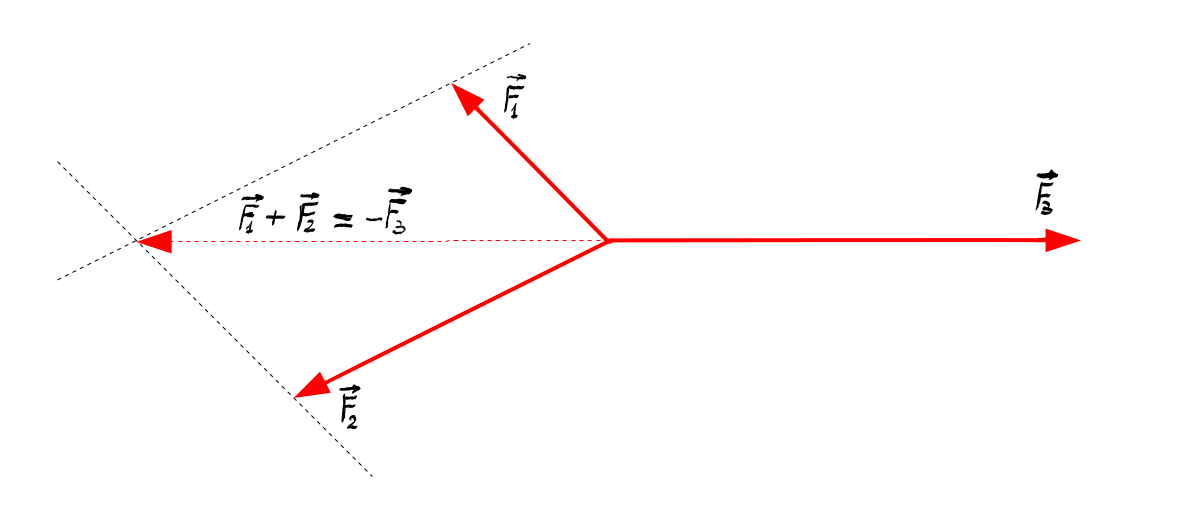
putem scrie felul următor F1 plus

F2 este egal cu minus f3 adică

rezultanta r a forțelor 1 și 2

suma lor este egal cu minus 3 după

cum se vede din această diagramă

putem foarte bine vedea Când se

întâmplă această situație Folosind

regula paralelogramului pentru

adunarea nu e frumușel doi Deci

F1 plus F2 adică r12 este acesta

acest Vector care va fi egal cu

minus f3 dar această ecuație de

echilibru mai poate fi scrisă și

Spre exemplu F1 Plus f3 egal cu

minus F2 adică R13 egal cu minus

F2 care la fel foarte ușor poate

fi obținută schematic din aceeași

diagramă dar adunând de data aceasta

vectorii 1 și 3 Deci folosim regula

paralelogramului construim folosind

vectori 1 și 3 un paralelogram

suma lor va fi diagonala de ce

acesta este R13 și întradevăr obținem

că R13 este egal cu minus F2 numai

desenez schema echivalentă Dar

putem scrie la ultimul caz F2 cruceas

3 este egal cu minus F1 care ar

însemna că r23 rezultanta forțelor

2 și 3 este egal cu minus unu în

concluzie în cazul echilibrului

punctului material supus acțiunea

trei forțe oricare dintre cele

trei forțe are magnitudinea egală

aceeași direcție dar sens opus

rezultantei celorlalte două forțe

cu altă concluzie importantă este

că în acest caz pentru ca echilibrul

ca punctul să se afle în echilibru

punctul de la intersecția celor

trei forțe se afle in echilibru

trebuie ca cele trei forțe să fie

coplanare dec 1 2 și f3 trebuie

să fie cu aplanare în același plan

altfel nu am putea avea aceste

relații Să considerăm urmatorul

exemplu de echilibru la translație

sub acțiunea trei forțe avem un

cablu atașat de un perete cu ajutorul

unui cârlig Care este tras la celălalt

capăt cu o forță orizontală f și

undeva la mijlocul cadrului se

află atașat un corp cu o greutate

G se dau masa corpului de 40 de

kg forța orizontală de 300 meniul

Toni Se știe că întreg sistemul

este în echilibru și dorim să aflăm

tensiunea din cablu atât magnitudine

A cât și orientarea exprimată prin

unghiul Alfa cu verticala și aceasta

va fi tensionate pe care dorim

să o afla punctul a se află în

echilibru de translație și deci

putem scrie că suma forțelor care

acționează în punctul A și anumite

plus b plus c este egal cu 0 după

cum am văzut asta implică că te

este egală cu minus aer unde e

r este rezultanta forțelor f și

g deoarece Forța f este orizontală

în cazul nostru orizontală și G

este întotdeauna verticală rezultă

că ef este perpendicular pe G și

Deci avem următoarele forțe în

punctul a orizontală din G verticală

între ele avem unghi de 90 de grade

ele vor da o forță rezultanta R

suma lor este egală cu el și datorită

faptului ca este în echilibru este

tensiunea va fi egală și de semn

sens opus lui unghiul Alfa Sing

acestea Deci aer pătrat este egal

cu x pătrat plus GPS aceasta este

teorema lui Pitagora care se poate

aplica datorită faptului că toate

aceste unghiuri sunt 90 de grade

Deci ipotenuza la patrat iar pătrat

egal cu suma catetelor la pătrat

pătrat si pătrată deci putem înlocui

300 de Newton la pătrat plus G

Care este masa 40 de kg amorțit

cu accelerația gravitațională pe

care o luăm egală cu 10 ani Deci

aproximam G cu 10 m pe secundă

la pătrat în loc de 9 pentru simplificarea

calcului rezultă că chiar este

egal cu 500 de Newton din prima

ecuație Ce rezultă din la echilibrului

a rezultă că tensiunea în cablu

va fi egala cu 500 de ani pentru

a calcula orientarea tensiunii

folosind faptul că tangență de

Alfa este egală cu F supra G deci

tangent de Alfa este cateta opusă

care este împărțită la cateta alăturată

Care este ce Deci 300 împărțit

la 400 m egal cu 0 rezultă că Alfa

este egal cu 37 de grade echilibrul

unui corp cu legături se numește

legătură orice cauză ce limitează

mișcarea unui corp exemple de legături

sunt firele resorturile pereții

sau suprafețele în contact cu corpul

luat în considerare cablurile și

așa mai departe Forțele de legătură

depind de tipul legăturii Forțele

de legătură din fier se numesc

tensiuni din resorturi se numesc

forțe elastice în cazul perete

sau unei suprafețe se numește forță

normală și așa mai departe Toate

aceste forțe de legături trebuie

adăugate la forța rezultantă si

nulă în cazul în echilibru de translație

pentru a exemplifica Să considerăm

următorul caz avem un plan înclinat

cununi Alfa pe care se află un

corp Ce este atașat de un Resort

Care este fixat cunoaștem greutatea

g a corpului unghiul Alfa al planului

înclinat și neglijăm forța de frecare

pentru moment în această problemă

Se mai Dădea semne și Constanța

elastică a resortului dorim să

calculăm în forțele de legătură

din această problemă știind că

corpul se află în echilibru de

ce este în echilibru Deci avem

o singură forță greutatea restul

fiind forță de legături să vedem

care sunt Forțele de legătură păi

în primul rând avem o forță de

legătură datorată resortului Care

este o forță de tip elastică este

zici prima forță de legătură este

este cea de a doua forță de legătură

este forța normală a suprafeței

Care este reacțiunea suprafeței

la acțiunea corpului prin greutatea

G asupra lui deoarece corpul este

în echilibru putem scrie că ge

plus n plus f e sunt egale cu 0

corpul este în echilibru asta înseamnă

că suma forțelor ce acționează

asupra lui este 0 alegem un sistem

de coordonate De ce alegem oxyg3n

forța elastică este egală cu componenta

greutății Da lungul axei x Deci

forța elastică este egală cu m

g sinus de Alfa și pe o y a avem

cealaltă forță de legătură și al

meu forța normală Care este egală

cu ceai de forța normală la ce

mgm cosinus de Alfa și acestea

sunt cele două forțe de legătură

ce limitează mișcarea corpului

forța elastică o limitează în direcția

o x forța normală o limitează în

direcția o fire sunt legate de

greutate prin aceste două relații

în cazul în care ce este negru