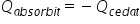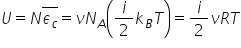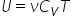Ecuaţia calorimetrică. Energia internă.

încet dar noua lecții de termodinamică

vom discuta despre următoarele

noțiuni de calorimetrie ecuația

calorii metrică și energia internă

calorimetrul este un dispozitiv

folosit pentru măsurarea schimbului

de căldură dintre un corp și un

mediu cu proprietăți cunoscute

în cele mai multe cazuri apă întreg

sistemul este izolat de un înveliș

adiabatic adică un înveliș care

nu permite schimbul de căldură

cu mediul extern cantitatea sau

mărimea cel mai des măsurată de

către un calorimetru este căldura

specifică a corpului studiat există

două tipuri de calorimetre în funcție

de tipul de schimb de căldură Ce

are loc între corp și mediul din

calorimetru cel mai cunoscut este

calorimetrul bertlo în care schimbul

de căldură are loc cu variația

de temperatură în interiorul sistemului

noi până acum am definit doar un

schimb de căldură Ce are loc cu

variații de temperatură Deci ați

putea spune că acesta putea fi

singurul fel de calorii metru totuși

există un schimb de căldură Ce

are loc fără variație de temperatură

despre care vom vorbi în întruna

din lecțiile viitoare de termodinamică

și anume schimbul de căldură Ce

are loc la schimbarea stării de

agregare Spre exemplu la evaporarea

unui lichid evaporarea apei are

loc fără va de temperatură dar

cu schimb de căldură pentru studierea

acestui tip de tip de căldură se

folosește așa numitul calorimetru

izoterm care Deci studiază schimbul

de căldură ce apare la schimbarea

stării de agregare și fără variație

de temperatură un calorimetru Folosește

două noțiuni fundamentale ale termodinamicii

prima este așa numitul principiul

0 al termodinamicii despre care

discuta în cea de a doua lecție

de termodinamică când am definit

temperatura și scările de temperatură

principiul 0 al termodinamicii

Stabilește proprietatea de tranzitivitate

echilibrului termic între mai multe

sisteme termodinamice și este necesar

de fiecare dată când măsurăm o

temperatură folosește de asemeni

așa numita ecuație calorimetrica

care spune foarte simplu că pentru

un calorimetru Care este un sistem

izolat de învelișul adiabatic Deci

nu face schimb de căldură cu exteriorul

căldura primită este egal cu minus

căldura cedată bineînțeles ne referim

la schimbul de căldură din interiorul

calorimetrului Haideți să vedem

cum se aplică în practică acest

folosirea acestui calorimetru și

a ecuației calorimetrice pentru

măsurarea călduri specifice a unui

corp Deci ceea ce vedeți în această

imagine este un dispozitiv tipic

de tip calorimetric și anume avem

un înveliș adiabatic format dintr

un strat dublu în interiorul căruia

se află aer la densitate foarte

mică ceva ce aproximează vidul

De ce are o tranzitivitate o capacitate

de a transmite temperatura foarte

mică suporții au această formă

tocmai pentru a minimiza suprafața

de contact dintre interior și exterior

Deci aceasta formează un înveliș

adiabatic în care schimbul de căldură

cu mediul exterior este 0 în interiorul

calorimetrului Avem apă purificată

și corpul a cărui proprietăți dorim

să le studiem de asemeni avem un

termometru pentru măsurarea temperaturii

sau un caz mai general mai multe

termometre pentru măsurarea temperaturilor

și Deci dorim să folosim acest

calorimetru Pentru a măsura căldura

specifică ce ce a corpului notat

cu ce cunoaștem masă corpului masa

apei și căldura specifică a apei

și capacitatea calorică k a dispozitivului

calorimetric măsurăm de asemeni

temperaturile inițiale ale corpului

și a apei pe touch ieșite Da am

și temperatura finală a întregului

sistem după ce echilibrul termic

sa stabilit în interiorul calorimetrului

Bineînțeles că dacă Reprezentăm

grafic temperatura care se măsoară

în grade Celsius ca funcție de

timp care se măsoară în secunde

vom porni de la anumită temperatură

a apei și o temperatură mai mare

te taie si a corpului și ce vom

observa este că Pe măsură ce echilibrul

termic dintre ele se obține ele

vor evolua Bineînțeles către o

temperatură comună mici obținem

o stare de echilibru termic la

după un anumit timp mergi după

un anumit timp se obține starea

de echilibru termic dintre corpurile

calorimetrului această temperatură

1 dăm cu teta fina De ce aceasta

este temperatura finală de echilibru

termic dintre corp și apă prin

apă înțelegem atât apa cât și cuva

adică dispozitivul calorimetric

în care a pus ea în timpul stabilirii

acestui echilibru termic corpul

va ceda căldură Deci vom avea o

căldură cedată care va fi primită

de către calorimetru adică apă

și cupru avea un Q primit căldură

primită ecuațiile pentru cele două

călduri sunt următoare căldura

cedată de corp va fi egală cu masa

corpului înmulțită Cu căldura specifică

a corpului înmulțită cu variația

de temperatură aceste definițiile

am dat în lecția precedentă această

ecuație venind din ecuația de definiție

a căldurii specifice de asemeni

pentru căldura primită de către

apă putem scrie ecuația următoare

căldura primită este egală cu masa

apei muncită Cu căldura specifică

a apei plus capacitatea calorică

a calorimetrului Deci prin apă

repet înțelegem atât apa cât și

cuva care o conține Deci k este

capacitatea calorică a acestui

disco Cities înmulțită cu variația

de temperatură a apei temperatura

finală a minus temperatura apei

și bineînțeles după cum am spus

folosim ecuația calorimetrica care

spune că căldura primită este egală

cu minus căldura cedată combinând

acestei ecuații putem scrie că

căldura specifică a corpului va

fi egală cu masa apei muncitor

căldura specifică a apei plus capacitatea

calorică a calorimetrului înmulțită

cu variația de temperatură a apei

împărțită la masa corpului și în

care este multă cu teta c temperatura

inițială a corpului minus temperatura

finală asta datorită semnului mini

observăm că toate mărimile din

această ecuație sunt pozitive tot

is minus teta apă este pozitiv

Deta c minus teta final Este pozitiv

Deci asta este felul în care se

folosește un calorimetru Pentru

a măsura căldura specifică a unui

corp oarecare să trecem la o nouă

noțiune cea de energie internă

energia internă se notează cu u

și este energia unui sistem termodinamic

ce se datorează mișcării și interacțiunii

atomilor sau moleculelor din interiorul

sau dacă considerăm un sistem termodinamic

are care avem două tipuri de energii

avem energii externe care sunt

de tip mecanic și le am studiat

în legile de conservare a energiei

și impulsului din mecanică ele

sunt una dată de mișcarea corpului

sau sistemului termodinamic an

întreg și eventual interacțiune

a sistemului nostru termodinamic

cu un alt sistem aceste energii

externe ale corpului de tip mecanic

sistemul are de asemeni și energii

interne aceasta Acestea se datorează

interacțiunilor dintre moleculele

sau atomii sistemului și mișcării

acestor molecule sau atomi Deci

când spunem energie internă referim

la energia din interior nu și la

energia din exterior cu care pe

care o are corpul ca un întreg

sau sistemul ca un întreg în cazul

unui gaz ce se nu se află la presiune

înaltă știm din lecțiile de teorie

cinetică moleculară că putem aplica

modelul gazului ideal Deci modelul

gazului de el după cum am stabilit

în acele lecții nu se poate aplica

lichidelor și solidelor sau gazelor

aflate la Sulina altfel gazele

la presiuni joase sau normale sunt

bine descrise de către acest model

cine acest caz putem neglija interacțiunile

dintre atomi și molecule și energia

internă va fi dată numai de mișcarea

lor iar această mișcare este deschisă

de energia cinetică medie Deci

energia internă a unui gaz ideal

va fi prin definiție egală cu numărul

de atomi sau molecule înmulțită

cu energia cinetică medie a unui

atom sau a unei molecule ecuația

pentru această energie cinetică

medie a fost dată în prima lecție

de teorie cinetică moleculară și

este aceasta deci putem scrie pentru

energia internă că este egală cu

numărul de moli înmulțită cu numărul

lui avogadro de aceasta vine din

definiția numărului avogadro Care

este numărul de atomi sau molecule

permis Deci numărul total va fi

numărul de moli înmulțit cu numărul

lui avogadro înmulțită cu ecuația

pentru cinetică medie care este

aceasta numărul de grade de libertate

înmulțit împărțit la 2 înmulțesc

Constanța lui boltzmann și te piși

temperatura din nou ecuația este

dată în prima lecție de teorie

cinetico molecular datorită faptului

că Constanța boltzmann este definită

ca raportul dintre Constanta mire

sau Constanța universală a gazelor

și numărul avogadro putem R scrie

ecuația pentru energie internă

în felul următor În fine ecuația

finală a energiei interne va fi

numărul de înmulțit cu cvt relația

folosită în particulară aceea Că

căldura specifică molară la volum

constant CV este egal cu numărul

de grade de libertate împărțit

la 2 înmulțit cu Constanța mire

va fi demonstrat în lecția viitoare

Deci această ecuație care a fost

folosită în pasul final al derivării

cu ei pentru energia internă va

fi demonstrată în lecția viitoare

împreună cu ecuația mai generală

numită ecuația mire și anume că

CP egal cu c v plus Deci pentru

aceste demonstrație lecția viitoare

o concluzie din această definiție

și Ecuația acompaniată a pentru

gaze deal este că energia internă

este un parametru de stare intensiv

reamintesc parametru de stare înseamnă

că ia o valoare dată pentru o stare

dată deci energia internă va avea

o valoare pentru o stare sau moment

dat în particular dacă avem un

proces termodinamic între două

stări termodinamice a și b energia

o va lua o valoare pentru fiecare

stare finală inițială sau intermediară

ea nu e o valoare pentru întreg

procesul si pentru fiecare stare

de a lungul procesului intensiv

înseamnă că nu depinde de volumul

sistemului ceea ce vedem direct

din ecuația pentru iarăși specifică

în această proprietate depinde

doar de temperatura sistemului

nu și de Volumul lui am demonstrat

acest lucru pe bază de origine

Tico moleculare Acest lucru se

demonstrează și experimental prin

așa numitul experiment jur de ce

experimentul experimentul Joule

Demonstrează că nu depinde de vie

și în fine pentru un sistem închis

și izolat energie internă este

constant sistemul închis înseamnă

un sistem în care masă sau dacă

vreți numărul de moli sunt constante

iar sistem izolat înseamnă cel

care nu schimbăm căldură sau dacă

vrei să te împărat ură cu mediul

extern din ecuația pentru energia

internă observăm că dacă atât nu

cât și te sunt constante atunci

Bineînțeles că este o constantă