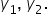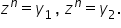Ecuații binome
Tag-uri
Partajeaza in Google Classroom

Transcript
ecuațiile binome sunt ecuații de
forma 10 la n minus a egal cu zero
unde 10 este număr complex n este
număr natural mai mare sau egal
cu 2 iar a este număr complex această
ecuație se mai poate scrie 10 la
n egal cu a în consecință rezolvarea
ecuațiilor se reduce la determinarea
rădăcinilor de ordinul n ale numărului
complex Iată câteva exemple avem
ecuația Jet la 6 minus 1 egal cu
0 această ecuație se va scrie 10
la a șasea egal cu 1 iar soluțiile
acestuia vor fi rădăcinile de ordinul
6 ale unității am discutat despre
aceste rădăcini în lecția trecută
un alt exemplu avem ecuația 10
la a treia plus 27 egal cu zero
această ecuație se mai poate scrie
z la a treia egal cu minus 27 și
Acum va trebui să găsim rădăcinile
de ordinul 3 ale numărului complex
minus 27 mai întâi vom scrie Acest
număr sub forma trigonometrică
vom avea 27 pe lângă minus 1 plus
0 ori e egal cu 27 pe lângă cosinus
de pi plus e sinus de pi am scris
Ba ceastă formă pentru că modulul
numărului complex adică acest număr
care apare în fața parantezei trebuie
să fie întotdeauna un număr pozitiv
cosinus de pi este minus unu ia
sinus de pi este 0 Așadar aceasta
va fi forma trigonometrică a numărului
complex minus 27 prin urmare modulul
este 27 iar argumentul redus va
fi fi rădăcinile de ordinul 3 ale
acestui număr complex vor fi de
K egal cu radical de ordinul 3
din 27 pe lângă cosinus de pi plus
2k pi supra 3 plus e sinus de pi
plus 2 k pi supra 3 unde e numărul
lui ta Ia valori de la 0 până la
2:00 să calculăm prima rădăcină
1000 radical de ordinul 3 din 27
este 3 pe lângă înlocuim numărul
ca cu 0 și obținem cosinus de pi
supra 3 plus e sinus de pi supra
3 egal cu 3 pe lângă 1 supra 2
plus radical din 3 supra 2 egal
mai departe cu 3 supra 2 plus 3
radical din 3 supra 2 e următoarea
rădăcină se obține pentru ca egal
cu unu și Avem 3 pe lângă cosinus
2 plus pai este 3 supra 3 simplificăm
cu 3 și ne rămâne pe plus e sinus
de pi cos de pi este minus unu
sinus de pi este 0 egal cu minus
3 de 2 va fi egal cu 3 pe lângă
4 p plus p este 5 p supra 3 plus
e sinus de 5.000 supra 3 egal vom
calcula mai jos cosinus de 5 supra
3 5pi supra 3 se poate scrie 6
Pi supra 3 minus y supra 3 egal
cu cosinus de 2 pi minus pi supra
3 perioada principală a funcției
cosinus este 2 pi asta înseamnă
că atunci când la un argument adunăm
sau scădem 2 pi valoarea funcției
cosinus rămâne neschimbată în consecință
vom avea egal cu cosinus de minus
pi supra 3 funcția cosinus este
pară egal mai departe cu cosinus
de pi supra 3 egal cu 1 pe 2 procedăm
asemănător și cu sinus de 5 p supra
3 parcurgem aceeași pași până aici
obținem sinus de minus pi supra
3 și nu zi este impară prin urmare
semnul minus va trece în față avem
minus sinus de pi supra 3 și înalt
cu minus radical din 3 supra 2
Revenim la calcule și Avem 3 pe
lângă 1 pe 2 minus radical din
3 supra 2 e egal cu 3 pe 2 minus
3 radical din 3 supra 2 e acestea
vor fi cele trei rădăcini ale ecuației
date să vedem o altă ecuație avem
ecuația 10 la a treia minus radical
din 3 minus 1 egal cu 0 această
ecuație se va scrie z la a treia
egal cu 1 plus radical din 3 E46
găsim rădăcinile de ordinul 3 ale
acestui număr complex voi nota
cu numărul complex 1 plus radical
din 3 și mai întâi vom exprima
acest număr sub forma trigonometrică
calculăm modulul numărului complex
un avem radical din 1 la a doua
plus radical din 3 la a doua obține
un radical din 4 egal 2 iar pentru
a găsi argumentul redus recomand
să Reprezentăm mai întâi în plan
punctul de coordonate 1 radical
din 3 Iată observăm că imaginea
geometrică a numărului complex
1 este un punct situat în cadranul
întâi tangentă de te este egal
cu radical din 3 Așadar unghiul
te va fi egal cu pi supra 3 radiani
și atunci numărul complex 1 va
avea formă trigonometrică 2 pe
lângă cosinus de pi supra 3 plus
e sinus de pi supra 3 acum Trebuie
să găsim rădăcinile de ordinul
3 ale acestui număr complex și
vom avea o k egal cu radical de
ordinul 3 din 2 pe lângă cosinus
de pi supra 3 plus 2k supra 3 plus
e sinus de pi supra 3 plus 2k supra
3 pentru ca luni valori de la 0
până la 2:00 prima rădăcină cu
zero va fi radical de ordinul 3
din 2 pe lângă cosinus de pi supra
3 totul supra 3 este pi supra 9
plus e sinus de pi supra 9 următoarea
rădăcină 1 va fi radical de ordinul
3 din 2 pe lângă dacă numărul ca
ia valoarea 1 avem 2pi plus p supra
3 amplificăm cu 3 ne dă 6 plus
pe 7 pi pe 3 totul supra 3 obținem
7 pe 9 plus sinus de 7 pi supra
9 și ultima de de cină cu 2 egal
radical indice 3 din 2 pe lângă
pentru ca luni valoarea doi avem
patru p plus p supra 3 ne dă 13
pi supra 3 și totul supra 3 vine
13 pe supra 9 plus e sinus de 13
pi supra 9 acestea au fost cele
trei rădăcini ale numărului complex
și soluțiile ecuației date și un
ultim exemplu avem ecuația x la
a patra minus 1 plus radical din
3 egal cu Z la a patra pentru început
vom trece numărul 10 la a patra
în primul membru și avem e z la
a patra minus 10 la a patra egal
cu 1 minus radical din 3 de factor
comun și obținem z la a patra pe
lângă a minus 1 egal cu 1 minus
radical din 3 la a patra va fi
egal cu 1 minus radical din 3 supra
minus 1 pe care îl voi scrie minus
1 plus e va trebuie Așadar să găsim
rădăcinile de ordinul patru ale
acestui număr complex pentru a
scrie Acest număr complex sub formă
trigonometrică voi nota cu 1 numărul
complex 1 minus radical din 3 cu
2 numărul complex minus 1 plus
e vom Scrie fiecare număr sub forma
trigonometrică și apoi vom calcula
raportul dintre cele două numere
modulul numărului complex 1 este
radical din 4 egal cu 2 pentru
a găsi argument redus al acestui
număr complex luăm reprezenta în
plan punctul de coordonate 1 și
minus radical din 3 cred că este
foarte util să Reprezentăm un plan
numerele complexe pentru a vedea
exact în ce cadran este situată
imaginea geometrică și astfel nu
vom greși atunci când calculăm
argumentul redus al numărului complex
Așadar să Reprezentăm un plan punctul
de coordonate 1 și minus radical
din 3 observi încă imaginea geometrică
a numărului 1 este situată în cadranul
4 acest unghi pe care o să notezi
cu alfa va fi al tangentă de radical
din 3 să scriem Alfa este arctangenta
de radical din 3 și egal cu pi
supra 3 și atunci argumentul acest
unghi 1 va fi egal cu 2 pi minus
pi supra 3 egal cu 5 supra 3 forma
trigonometrică a numărului complex
1 este 2 pe lângă cosinus de 5
p supra 3 plus e sinus de 5.000
supra 3 mai departe scriem numărul
u2 sub formă trigonometrică modulul
numărului complex u2 va fi radical
din 2 și aici Reprezentăm punctul
de coordonate minus unu unu Iată
imaginea geometrică a numărului
u2 este un punct situat în cadranul
al doilea pe 2 este argumentul
redus acest unghi pe care îl putem
nota cu Betta are măsura egală
cu 45 de grade pentru ca sa format
un triunghi dreptunghic isoscel
este pi supra patru și atunci unghiul
T2 va fi egal cu pi minus pi supra
4 egal cu 3 supra 4 Acum putem
să scriem forma trigonometrică
a numărului complex u2 Roman radical
din 2 pe lângă cosinus de 3 pi
supra 4 plus e sinus de 3pi supra
4 10 la a patra este raportul dintre
numerele 1 și 2 egal aici avem
forma trigonometrică a numărului
1 iar Aici este cu 2 m avea 2 pe
lângă cosinus de 5 p supra 3 plus
e sinus de 5.000 supra 3 totul
supra radical din 2 pe lângă cosinus
de 3 pi supra 4 plus sinus de 3pi
supra 4 2 supra radical 2 este
radical din 2 pe lângă cosinus
argumentele se scade atunci când
împărțim două numere complexe trebuie
să efectuăm scăderea 5pi supra
3 minus 3 pi supra 4 ne dă 20 minus
9 pi totul supra 12 egal cu 11
pi supra 12 avem Așadar cosinus
de 11 pi supra 12 plus e sinus
de 11 pi supra 12 noi trebuie acum
să scriem rădăcinile de ordinul
4 ale acestui număr complex notăm
numărul acesta complex cu un rădăcinii
de ok pa nu fii radical de ordinul
4 din radical din 2 pe lângă cosinus
de 11 pi supra 12 plus 2 capii
totul supra 4 plus e sinus de 11
pi supra 12 plus 2 capii totul
supra 4 pentru ca luni valori de
la 0 la 3:00 putem să notăm și
cu Zed ca aceste rădăcini nu are
importanță voi calcula prima rădăcină
o 0 iar celelalte va rămân temă
cu zero va fi egal cu radical indice
8 din 2 pe lângă cosinus de 11
pi supra 12 ori 4 este 48 plus
e sinus de 11 pi supra 48 celelalte
rădăcini u1 u2 și cu 3 se obțin
pentru ca luni valorile 1 2 respectiv
3

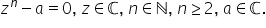
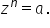
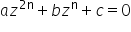
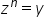 și se rezolvă ecuația
și se rezolvă ecuația 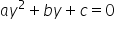 cu soluțiile
cu soluțiile