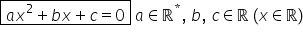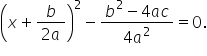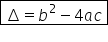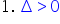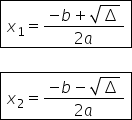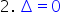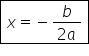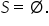Ecuații de gradul al doilea
Tag-uri
Partajeaza in Google Classroom

Transcript
să vorbim acum de ecuația de gradul
al doilea cu o necunoscută o asemenea
ecuație are această formă a ori
x pătrat adunat cu b ori x adunat
cu c egal cu 0 unde a b și c sunt
toate numere reale iar în plus
a este un număr real nenul a diferit
de 0 De ce se numește ecuație cu
o necunoscută foarte simplu pentru
că avem o singura necunoscută la
noi necunoscuta este x De ce se
numește de gradul al doilea pentru
că cea mai mare putere la care
apare necunoscuta este puterea
a doua avem aici x pătrat și x
la întâia Deci x la a doua e cea
mai mare putere la care apare x
și un exemplu este acesta x pătrat
minus 5 ori x este egal cu minus
11 supra 2 acum dacă vrem ca această
ecuație să aibă formă scrisă observăm
că membrul din dreapta în această
parte este 0 atunci îl trecem pe
minus 11 pe doi Peste egal cu semn
schimbat și vom avea x pătrat minus
5 ori x plus 11 supra 2 egal cu
0 aceste Două ecuații sunt ecuații
echivalente Cum rezolvăm o asemenea
ecuație vrem să grupăm termenii
care conțin necunoscuta și să formăm
un pătrat perfect pentru că aici
ne apare x la pătrat și pentru
aceasta vom scrie în felul următor
avem x la a doua minus 5 ori x
îl vom scrie 2 ori 5 supra 2 ori
x și o să înțelegeți imediat De
ce îl scriem așa Iată avem aici
un număr ridicat la pătrat minus
2 ori numărul respectiv înmulțit
cu 5 supra Păi dacă adunăm noi
pătratul lui 5 supra 2 adică 5
supra 2 totul la a doua atunci
ce vom avea aici e o formulă cunoscută
și o să obținem x minus 5 supra
2 totul la pătrat și am obținut
un pătrat perfect în care avem
necunoscuta însă nouă nu ne apare
aici 5 supra 2 totul la pătrat
ce avem 11 supra 2 Cum facem pe
casă nu modificăm cu nimic ecuația
noastră pentru că Iată Nici aici
nu am modificat 2 cu 2 se simplifică
și ne rămâne cinci ori x Exact
aici casă nu modificăm nici aici
atunci am adunat acest termen îl
și scădem Deci minus 5 supra 2
la totul la pătrat și adunăm termenul
nostru adică plus 11 supra 2 egal
0 această diferență ne dă 0 Deci
ne rămâne 11 supra 2 Exact aici
de ce aceste Două ecuații sunt
echivalente Bun Aici am obținut
această pătratul aceste diferențe
și crezi tu copie minus ridicăm
la pătrat avem 25 supra 4 plus
60 de să amplificăm cu doi și vom
avea 22 supra 4 egal 0 și facem
calculul x minus 5 supra 2 totul
la pătrat și aici vom avea minus
3 supra 4 egal cu zero Păi deja
e mult mai ușor să rezolvăm o asemenea
ecuație decât cea de la care am
plecat pentru că Iată acest termen
3 supra 4 Cum îl putem scrie Păi
putem să facem în așa fel încât
să avem o diferență de pătrate
face este un număr pozitiv deci
putem să îl scriem radical din
3 supra 2 totul deci totul la a
doua Haide să se vadă mai bine
ce vom obține avem x minus 5 supra
2 totul la pătrat minus acest termen
egal cu 0 cum a spus diferență
de pătrate desfacem această diferență
avem x minus 5 supra 2 Deci acest
termen minus ce avem aici Deci
minus radical din 3 supra 2 înmulțit
cu suma dintre acest termen x minus
5 supra 2 adunat cu radical din
3 pe 2 de ce Am aplicat formula
diferenței de pătrate nu am făcut
nimic egal cu 0 Deci nu am făcut
nimic nou și acum când un produs
de două numere reale ne dă 0 când
cel puțin unul din numere este
0 Deci fie a avem acest număr egal
zero adică x minus supra 2 minus
radical din 3 pe 2 egal 0 sau putem
să avem această variantă în care
x minus 5 supra 2 plus radical
din 3 supra 2 ne dă 0 alte cuvinte
aici vom avea echivalente cu X
cât ne dă Păi trecem fiecare termen
peste egal cu semi schimbat și
vom avea așa numitorul este doi
și avem 5 plus radical din 3 5
plus radical din 3 pe 2 sau x este
egal cu vom avea aicea 5 minus
radical din 3 supra 2 deci de fapt
Avem două soluții și putem să le
notăm diferit X1 și X2 am obținut
pentru această ecuație două soluții
și notăm soluția este să notăm
aici sub avem cinci plus sau minus
radical din 3 supra 2 deci trecem
linia de fracție 5 plus sau minus
radical din 3 supra 2 Și acum Haideți
să găsim metoda de rezolvare pentru
o ecuație de gradul al doilea scris
în Forma generală iar Forma generală
este aceasta avem ax pătrat plus
bx plus c egal cu 0 ca să construim
mai ușor pătratul din care face
parte necunoscuta mă refer la acest
pătrat ar trebui ca acel coeficient
a lui x pătrat să fie egal cu unu
bun însă noi avem coeficientul
lui x pătrat egal cu a Cum să facem
ca locul lui a să fie 1 foarte
simplu a este diferit de 0 de aceea
putem să împărțim această egalitate
chiar la ei tragem o bară verticală
și împărțim la ei și vom avea Haideți
să facem acesta mai mare se vadă
a împărțit la n de 1 Deci vom avea
x pătrat adunat cu b supra a înmulțit
cu x adunat cu c supra a egal cu
zero și acum haide să construim
pătratul Deci avem x pătrat pe
care îl copiem adunat cu 8 3 cm
aici 2 înmulțit cu pi dacă înmulțim
acest produs cu doi ca el să nu
se modifice trebuie să îl împărțim
tot la 2:00 Deci vom avea b supra
2 ori a înmulțit cu x Iată doi
cu doi se simplifică Deci ne rămâne
b supra a oryx exact ce avem aici
adunat cu acum ca să formăm pătratul
de ce mai avem nevoie Păi avem
x pătrat adunat cu 2 ori x înmulțit
cu b supra 2 ora de ce avem nevoie
de pătratul acestui Factor b supra
2 ori a totul la pătrat ca să nu
se modifice cu nimic ecuația noastră
scădem ce am adăugat b supra 2
ori a totul la pătrat adunat cu
termenul nostru ce aveam aici adică
ce supra a egal cu zero Iată aici
obținem 0 această diferență ne
dă 0 plus c supra adică ce aveam
mai sus Cele Două ecuații scrise
sunt echivalente primii trei termeni
vom folosi formula știută și vom
obține x adunat cu b supra 2-a
totul ridicat la pătrat minus și
aici ai de să facem calculul avem
b pătrat supra 4-a la a doua chiar
putem să amplificăm cu 4-a și vom
avea la numitor 4-a pătrat iar
la numărător 4-a cuțit cu c egal
cu 0 Deci obținem x plus Deci aici
avem plus b supra 2-a totul ridica
la pătrat și aici se restrânge
în calculul Vom avea în minus linie
de fracție 4 la a doua ce avem
la numărător apoi minus b pătrat
minusul de jale am scos în față
aici trebuie să obținem plus pe
sistem trecem aici minus ori minus
ne dă plus Deci om avea de pătrat
minus 4 ac egal cu 0 iar minus
b pătrat minus b pătrat minus ori
minus de de plus acest termen exact
ce avem aici până la acest moment
nu am făcut nimic Decât să parcurgem
pașii așa cum am făcut și la această
ecuație și acum ca să ne fie mai
simplu Haideți să notăm această
diferență cu Delta și notăm aici
Delta egal cu b pătrat minus 4
a c și să se vadă mai clar Voi
păstra doar această ecuație bun
Haideți să păstrăm nu chiar ultima
forma ba chiar să lăsăm doar ultima
formă pentru că vom avea nevoie
de spațiu descriere Delta se numește
discriminantul și vom nota discriminantul
ecuației a x pătrat plus bx plus
c egal 0 adică discriminantul ecuației
date inițial iar acum vom avea
folosind această scriere cu Delta
x plus b supra 2-a totul ridicat
la pătrat minus Delta supra 4-a
pătrat ne dă 0 de ce folosim denumirea
de discriminant pentru că această
diferență exact ce avem aici face
deosebirea între soluțiile ecuației
noastre cu alte cuvinte discriminantul
hotărăște să zicem așa Ce fel de
soluții are această ecuație discriminantul
este un număr real Păi asta înseamnă
că el poate să fie ce ai de să
notăm poate să fie strict mai mic
decât 0 sau poate să fie egal cu
0 sau poate să fie strict mai mare
decât 0 Deci avem una din aceste
trei variante pe care le am și
notat Ce se întâmplă dacă discriminantul
este un număr negativ Păi Haideți
să ne uităm aici Patru a la a doua
este un număr strict pozitiv da
Deci asta înseamnă că toată această
fracție Cum va fi numărătorul e
negativ numitorul e pozitiv Deci
vom obține că Delta supra 4-a este
strict mai mic ca 0 cu minus în
față înseamnă caminos Delta supra
4-a pătrat pardon Aici am scris
doar patru a va fi cam strict mai
mare ca 0 Păi ce soluții vom obține
pentru această ecuație Haideți
să dăm chiar un exemplu concret
ca să înțelegeți mai bine dacă
Delta e de exemplu minus unu Deci
cazul Delta strig negativ vom avea
urmări mic x plus b supra 2-a totul
la pătrat minus acest minus Delta
care ne dă minus 1 supra 4-a pătrat
egal 0 2 minus ori minus ne dă
plus Deci vom avea x plus b supra
2-a totul la pa plus 1 supra 4-a
pătrat ne dă 0 Ce fel de număr
iar sista strict pozitiv ce fel
de număr Acesta e pătratul unui
număr real De ce mai mare sau egal
cu 0 Păi putem noi să adunăm un
număr mai mare sau egal cu 0 cu
1 strict pozitiv iar rezultatul
să fie 0 nu de centru asemenea
situație în care Delta este negativ
strig negativ nu avem soluții de
soluția este mulțimea vidă Haide
să ștergem aici și vom nota rezultă
că soluția este mulțimea vidă Deci
dacă discriminantul e un număr
negativ nu avem soluție pentru
ecuația noastră dacă discriminantul
este 0 vom obține avem aici 0 supra
4-a pătrat Deci ne dă 0 Deci x
plus b supra 2-a la pătrat cât
ne dă 0 Păi asta echivalent cu
a spune că ce avem aici x plus
b supra 2-a ne dă 0 echivalent
cu x egal cu minus b supra 2-a
Deci notăm că soluția este minus
b supra 2-a de ce în situația în
care discriminantul este 0 avem
o singură soluție și anume aceasta
dacă discriminantul este un număr
strict mai mare ca 0 atunci ce
o să rezulte Păi vom avea exact
situația descrisă în exemplul nostru
când am rezolvat prima ecuație
având aici un număr strict pozitiv
pentru că acum Delta supra 4-a
pătrat va fi strict pozitiv putem
să îl scriem ca fiind pătratul
unui număr concret vom avea Deci
rezultă rescriem x plus b supra
2-a totul la pătrat minus radical
din Delta pe care putem să scriem
acum pentru că Delta este strict
pozitiv supra 2-a totul la pătrat
egal cu 0 și acum facem exact ce
am făcut inecuația noastră desfacem
diferența de pătrate de x plus
b supra 2-a minus ce avem aici
radical din Delta supra 2-a totul
un pardon nu totul la pătrat Deci
totul în paranteză înmulțit cu
x plus ce avem aici b supra 2-a
Și acum ce trecem adunat cu acest
radical din Delta supra 2-a ne
dă 0 și ce variante avem Păi fie
obținem aici 0 și obținem aici
0 și vom avea de fapt că x plus
b supra 2-a minus radical din Delta
supra 2-a ne dă 0 sau exact cum
scrie și în ce alt exemplu ce avem
aici adică x plus b supra 2-a plus
radical din deltă supra 2-a ne
dă 0 e deja e simplu aici pentru
că x va fi egal cu trecem numitorul
comun care este 2-a și vom avea
minus b plus radical din deltă
supra 2-a sau avem varianta următoare
tot așa numitorul este 2-a minus
b minus radical din deltă supra
2-a de ceartă că și aici Avem două
soluții X1 și X2 Deci notăm că
în acest caz soluția va fi trecem
numitorul Care este 2-a minus b
plus sau minus radical din deltă
supra 2-a raționamentul pe care
îl am făcut aici nu este unul simplu
nu mai este nici foarte complicat
și îl am făcut pentru că am vrut
să vedeți că ai de se vadă și Delta
am vrut să vedeți de unde apare
necesitatea de a calcula această
diferență de ce numim această diferență
discriminant Și de ce e nevoie
să luăm în calcul la aceste trei
variante pentru Delta pentru că
de fapt iată că Delta decide Ce
fel de soluție are ecuația noastră
acum să facem o scurtă recapitulare
când ni se dă o ecuație de gradul
al doilea Cum procedăm ca să o
rezolvăm mi se dă o ecuație de
gradul al doilea mai întâi calculăm
discriminantul acestei ecuații
și discriminantul este egal cu
trebuie să învățăm această formulă
sau pe de rost avem pătratul coeficientului
lui x adică b pătrat minus 4 înmulțit
cu a înmulțit cu ce Deci minus
patru ace și apoi în funcție de
Delta bun Stabiliți soluțiile avem
trei variante Delta este strict
mai mic ca 0 sau Delta este egal
cu 0 sau ultima variantă Delta
este un număr prim mai mare ca
0 dacă Delta este strig negativ
De ce obținem aici atunci soluția
acestei ecuații este mulțimea vidă
dacă Delta este 0 avem o singură
soluție și ea este dată de elementul
a minus b supra 2-a aceasta este
mulțimea soluțiilor și dacă Delta
este un număr strig mai mare ca
0 atunci vom avea două soluții
pardon și anume trecem linia de
fracție b Deci coeficientul lui
x cu minus în față plus sau minus
radical din deltă Care este un
număr real pentru că Delta este
strict pozitiv totul supra 2 înmulțit
cu coeficientul lui x pătrat adică
doi A deci ca să rezolvăm corect
o ecuație de gradul al doilea trebuie
să urmărim această schemă și evident
Să știm și formulele care apar
în secvența ce urmează chiar o
să rezolvăm câteva ecuații de gradul
al doilea