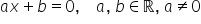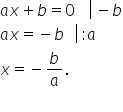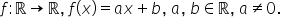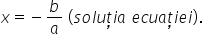Ecuații de gradul I

în această lecție vom face o recapitulare

a ecuațiilor și inecuațiilor de

gradul întâi Sper că Forma generală

a ecuației de gradul întâi este

dată așa cum vă reamintim din clasele

primare de a x plus b egal cu 0

unde a este diferit de 0 și a și

b sunt numere reale plecând de

la ideea teoretică ar trebui să

înțelegeți în practică cumva că

variabilă x poate reprezenta prețul

unui bun pe care îl propune cel

achiziționa numărul are el poate

să reprezinte cantitatea de bunuri

achiziționate numărul b real poate

reprezentat suma de bani cheltuită

pentru achiziționarea acestor astfel

se poate da un exemplu cât se poate

de ușor de simplu și anume bunuri

pe care vă Propuneți îl achiziționați

admitem că este un cantitatea de

bunuri pe care doriți să le achiziționați

este trei Deci În cazul ăsta vă

Propuneți să cumpărați trei tricouri

suma cheltuită pentru aceste tricouri

pentru achiziționarea acestor bună

este 45 chest caz ecuația de gradul

întâi ce ar descrie exemplul prezentat

ieri trei tricouri minus 45 RON

egal cu 0 minus 4 și 5 RON minus

spun deoarece banii au fost cheltuiți

ăsta este motivul pentru care inecuația

apare cu minus 45 de luni 0 RON

rezultat reprezintă suma de bani

pe care o aveți în acest moment

în buzunar după ce evidență ați

făcut achiziționarea de aceste

trei tricouri logic și normal trei

tricouri costă 45 de RON un tricou

va costat 45 de RON pățit la 3

astfel că valoarea unui tricou

este de 15 RON 500 exemplu e cât

se poate de simplu și de logic

în real life modalitatea teoretică

de rezolvare a ecuațiilor de gradul

întâi poate fi descrisă în felul

următor ecuația de gradul întâi

a x plus b egal cu zero va conduce

fără doar și poate la a x egal

cu minus pe prin trecerea lui b

în partea dreaptă cu sens schimbat

în această situație valoarea lui

x x fiind necunoscută variabilă

sau rădăcină a ecuației de gradul

întâi Deci așa cum spunea x va

avea valoarea meanness b supra

a cu Evident condiția de existență

a diferit de 0 vă dați seama că

în momentul în care ar avea valoarea

0 aș avea o fracție care are la

numitor 0 r pentru care b supra

0 b oricare ar fi el Da nu își

va avea semnal valoare cu fără

sens este motivul principal și

corect real pentru care a este

diferit de când de la exemplul

anterior vom avea 3x minus 4 și

5 egal cu 0 3 4 si seminte rar

numărul de tricouri pe care îl

achiziționați x este defapt un

tricou valoarea unui tricou 45

era suma cheltuită astfel că 3X

egal cu 45 minus 45 A trecut în

partea dreaptă cu sens schimbat

De ce a venit cu plus 45 x va fi

de 4 și 5 pe 3 și așa cum am lămurit

x va fi egal cu 5 cm a unei ecuații

de gradul întâi se poate face dacă

ajung la funcții de gradul întâi

astfel că graficul funcției de

gradul întâi f definită pe r cu

valori in R cu f de x egal cu ax

plus b vedeți ecuația de gradul

întâi transpusă repet între o funcție

este o dreaptă care intersectează

axa o x în punctul de abscisă a

minus b supra a Ce înseamnă asta

în primul rând că a minus b supra

este de fapt soluția respectiv

rădăcina ecuației ax plus b egal

cu zero ceea ce am afirmat mai

sus Da Și foarte foarte important

pentru descrierea geometrică pentru

reprezentarea grafică respectiv

interpretarea geometrică a funcției

de gradul întâi este important

să să înțelegeți că în primul rând

se face așa numita intersecție

cu axele de coordonate astfel că

vom considera că a și b sunt pozitive

și foarte important vom realiza

aceste intersecție cu axele de

coordonate pentru x egal cu 0 înțeleg

De fapt că este 0 egal cu a ori

0 plus b d c f de 0 va fi pe pat

de coordonate 0 b pentru alcool

0 ax plus b egal cu zero adică

x egal cu minus b supra a rezolvare

ecuație de gradul întâi se obține

în acest moment un pe mail Pe coordonate

minus pe supra important să înțelegeți

aici că Intersecția cu axele de

coordonate când fac x egal cu 0

de fapt fac Intersecția cu Axa

o y atunci când scriu y literă

cu zero fac de fapt Intersecția

cu Axa o x furca un sistem cartezian

x o y reprezentarea grafică așa

cum spuneam va fi o dreaptă ce

fain târsei axa o x în punctul

de abscisă a minus b supra a mică

dreapta reprezentată de mine cu

verde târcă aul de coordonate 0

și b acum tu la mare de coordonate

0 b este reprezentat aici b de

coordonate minus pe supra așa cum

spuneam există imens pe sufla vrea

și zero de reprezentat aici Astfel

că a apei va fi reprezentarea grafică

a funcției f definită pe r cu valori

in R Unde f de x egal cu ax plus

pe Da Și foarte important abscisa

este minus b supra și întotdeauna

se va reprezenta pe axa o x iar

ordonata este b și Cu siguranță

va fi reprezentată axa o y un exemplu

pentru rezolvarea ecuațiilor de

gradul întâi este dat de următoarea

aplicație să se rezolve ecuația

în x și anume a minus X egal cu

1 minus m pătrat x foarte important

în acest moment este să înțelegeți

că ecuația dacă are drept necunoscută

variabilă x deși apare parametrul

m în descrierea ecuației acesta

nu are efect asupra algoritmului

de rezolvare al ecuației asta înseamnă

că în momentul în care mă uit la

ecuație A minus X egal cu 1 minus

m pătrat ia de vine minus x conține

variabila x și rămâne în partea

stângă și plus m pătrat x iar conține

variabila x pentru care din dreapta

a fost adus în stânga cu semn schimbat

egal cu unu unu la rămas pe locul

lui in dreapta Deci nu sa schimbat

semnul minus m m a venit în partea

dreaptă Deci având plus a venit

cu semn schimbat de pe trebuie

observat faptul că am separat în

stânga termenii ce conțin variabila

x dar așa cum spuneam minus x plus

m pătrat x Da ele ca și termin

conțin variabila x iar în dreapta

restul de termeni 1 respectiv minus

Sami a nu conțin variabila Nica

este cea care contează pentru că

așa cum spuneam ecuația este rezolvată

în x are drept necunoscută x m

e un simplu parametru în de care

se rezolvă ecuația dată astfel

că voi da X factor comun relația

de mai sus și foi obține minus

1 plus m pătrat în paranteză egal

cu unu minus foarte important este

înțelegeți că de fapt x pe lângă

minus 1 plus m poate fi scris ca

minus 1 plus m pătrat torex asta

ca să înțelegeți în mod clar că

paranteză a mea este aul Teoretic

din ecuația din Forma generală

a ecuației de gradul întâi și rezultatul

Adică 1 minus semi este de fapt

minus beiul Teoretic astfel că

x sul va avea valoarea 1 minus

3 supra minus 1 plus m pătrat ceea

ce înseamnă că dacă dau minus în

față scot minus Factor forțat dacă

vreți sus la numărător voi obține

minus A minus 1 supra m pătrat

minus unu în mod egal se pun condiții

de existență al acestui rezultat

și mai clară a fracției obținute

și mai clar că așa cum spuneam

numitorul trebuie să fie diferit

de 0 în acest caz m pătrat minus

unu diferit de 0 de unde fără doar

și poate pricepem pătrat este diferite

unul de unde m este diferit de

plus și minus în rezolvarea clară

a ecuației continuu prin a spune

fina descrie că x paria bila noastră

este minus A minus 1 supra a minus

1 pe lângă n plus 1 acesta fiind

un o diferență de pătrate formulă

de calcul prescurtat aplicat și

atunci în mod Evident A minus unu

cu emisiuni se reduc înțelegând

in aceasta că e xul va avea valoarea

minus 1 supra n plus 1 continuare

vă comentez și este ideal să rețineți

că este important să înțelegeți

că punerea condițiilor distanță

în aceste cazuri este esențial

Sper că în ecuația dată de ecuația

pe care o Descrie a mai sus și

anume minus 1 plus m pătrați de

lângă x egal cu 1 si mie niste

pentru m egal cu 1 aduceți aminte

că mă rog ca și condițiile de existență

îmi trebuia să fie diferit de 1

respectiv admitem însă că nu am

puța chestie condiții de existență

și atunci să vedem ce sar întâmplat

dacă nu aș pune condițiile de existență

reveniți spun dacă m egal cu unu

în relația de mai sus voi avea

minus 1 plus 1 la pătrat eurex

egal cu unu minus unu înlocuind

cu nașa Cum se vede Da înțeleg

din asta ca voi obține 0 ori x

egal cu 0 o relație adevărată oricare

ar fi x real ce se întâmplă însă

în situația în care omul ar avea

valoarea minusul să le avea minus

1 plus minus 1 la puterea a doua

înmulțit cu x egal cu 1 minus minus

Asta înseamnă de fapt minus 1 plus

minus 1 x care egal cu 1 plus 1

Ceea ce va însemna realitate că

am 0 ori x egal cu 2 Asta înseamnă

de fapt o relație ce nu poate fi

verificată pentru nicio valoare

a lui x real adică ceva neadevărat

de pizde 0 egal cu 2 este o relație

falsă de reținut după parcurgerea

acestei direcții este că ecuațiile

de gradul întâi au necunoscuta

x ul la puterea maximă 1 Da Și

foarte important ecuațiile de gradul

întâi au o singură soluție reală