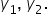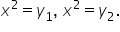Ecuații de gradul II cu soluții complexe
Tag-uri
Partajeaza in Google Classroom

Transcript
în această lecție ne vom opri asupra
rezolvării ecuațiilor de gradul
al doilea mai clar situația în
care aceste Tipuri de ecuații acceptă
soluții complexe pentru o lecție
precedentă am discutat despre rezolvarea
ecuațiilor de gradul al doilea
și nu am referit strict la situația
în care soluțiile acestora erau
reale în cazul în care de ecuații
lor era pozitiv practic mai mare
decât 0 sau mult adică egal cu
0 rezolvarea acestor Tipuri de
ecuații a fost comentat în această
lecție ne vom referi la situația
în care discriminantul este negativ
practic mai mic decât 0 ani care
mini situații pe care la acel moment
nu puteam de scrie pentru că nu
eram familiarizat conceptul de
număr complex mai clar la acel
moment ne rezumam la ideea nu avem
soluții reale în aceste condiții
în măsură să afirmăm că o ecuație
de gradul al doilea are soluții
complexe dacă discriminantul este
negativ așa dar dacă Delta este
mai mic ca 0 rădăcinile ecuației
x pătrat plus bx plus c egal cu
0 cu foarte importanta diferit
de 0 sunt numere complexe mai mult
rădăcinile numere complexe conjugate
vă reamintesc formula era x12 egal
cu minus b plus minus radical din
drepta supra 2-a în aceste condiții
Un ar fi minus 2 plus radical din
Delta supra 2 respectiv 2 arhivă
spre minus radical din Delta supra
2-a vă reamintesc că atunci când
vorbeam de numere complexe conjugate
aveam de forma Zi tu nu cu a plus
b a respectiv conjugat la acestuia
dezdoi era a minus b e aici de
plus respectiv minus deci de aici
și ideea că rădăcinile sunt numere
complexe conjugate atunci când
din calculul discriminantul Uite
tai calcul pe pătrat minus patru
ace se obține o valoare negativă
este necesar să traducem valoarea
obținută utilizând unitate imaginară
e astfel dacă Delta egal minus
o valoare un număr atunci pot scrie
ca minus 1 ori număr Da cam minus
1 este pătrat Delta se va traduce
așa cum spuneam ca fiind e pătrat
înmulțit cu număr în aceste condiții
radical din Delta necesar pentru
calculul rădăcinilor X1 X2 va fi
egal cu radical din x pătrat ori
număr ceea ce înseamnă de fapt
că este egal cu e radical din muma
Deci dacă am Ecuația a x pătrat
0 cu a diferit de 0 și terta calculat
pe pătrat minus 4 AC cu rădăcinile
calculate minus pe plus minus radical
din Deta supra 2-a spuneam secta
este negativ atunci rădăcini X1
X2 se pot traduce ca minus b plus
minus spuneam e radical din acel
număr numărul este de fapt 4-a
c minus pe pătrat întrucât acesta
fiind negativ vă dați seama că
4 a c minus b pătrat este practic
un număr pozitiv Deci X1 va fi
minus pe minus radical din 4 a
c minus b pătrat supra 2-a respectiv
2 va fi minus pe plus e radical
din 4 a si mie niste pătrat supra
2-a înainte de a trece la discutarea
unor exemple vă reamintesc că lecția
aferentă ecuațiilor de gradul al
doilea comentam despre suma rădăcinilor
suma notată cu X mare și de prezenta
X1 și X2 iar formula de calcul
a la minus b supra a produsul rădăcinilor
X1 X2 notat cu p avea ca și formulă
de calcul ce supra și în plus scrierea
trinomului de gradul al doilea
ax pătrat pe explice ca fiind a
pe lângă x minus x 1 pe lângă x
minus toate acestea sunt valabile
Da și se pot aplica și în situația
în care avem rădăcini complexe
exemple primul exemplu x pătrat
plus x plus 1 egal Deltă așa cum
știam de pătrat minus patru ace
Delta calculat și obținut este
minus 3 negativ așa cum se vede
drept pentru care îl putem scrie
ca fiind minus 1 înmulțit cu 3
dar așa cu neam lămurit minus 1
este pătrat Deci Delta va fi de
fapt pătrată radical din Deta va
fi e radical din 3 x 1 x 2 conform
formulei minus plus minus radical
din Deta supra 2-a moment în care
înțeleg că X1 este minus 1 minus
radical din 3 supra 2 respectiv
X2 este minus 1 plus radical din
3 supra 2 încă o dată Observați
că se rădăcini complexe conjugate
În condițiile în care minus 1 pe
2 îl regăsim la X1 și la X2 ca
fiind practic Paul Da iar fiul
da în cazul rădăcini X1 este minus
radical din 3 supra 2 iar în cazul
rădăcinii X2 de unde este Cati
supra 2 una doilea exemplu x pătrat
plus 4 egal cu zero x pătrat egal
cu minus 4 în mod Evident trece
cu semn schimbat momentul în care
iar înțeleg că în mulțimea numerelor
reale ceva ridicat la pătrat nu
putea să dea cu nimeni da deci
pătratul unei valori în garantat
pozitiv astfel acest minus patru
este tradus ca fiind produsul dintre
minus 1 și 4 minus 1 este motiv
pentru care x y 2 va fi plus minus
radical din 4 e pătrat ceea ce
înseamnă fără doar și poate că
X1 și X2 sunt plus minus doi i
rădăcini complexe Iași Acum am
înțeles Ba mai mult pot să înțeleg
că X1 egal cu 0 plus 2 E respectiv
x 2 egal cu 0 minus 2 încă o dată
ceea ce am afirmat mai sus este
dovedit rădăcini complexe conjugate
1 Tim exemplu să se simplifice
fracția x la a treia plus x pătrat
plus x plus 1 supra x la a treia
plus 1 minus x pătrat minus x Observați
că la numitor am o expresie matematică
de gradul al treilea și foarte
important coeficienții acestora
sunt complexe numărătorul x x pătrat
plus x plus 1 se dă între primele
două x pătrat factor comun iar
următoarele două sunt efectiv cuplate
intru paranteză x plus 1 factor
comun și pe lângă x pătrat plus
1 coeficientul pe care în realitate
el are x plus unu în paranteză
RMN de discutat cu x pătrat plus
1 egal cu 0 ca să determine soluțiile
și ca să folosesc acea disc lui
de gradul al 2 astfel x pătrat
egal cu minus 1 x pătrat Praktiker
pătrat ceea ce înseamnă de fapt
îi sunt doi este egal cu plus minus
ce soluții care atrag de la tine
că x pătrat plus 1 se va scrie
ca 1 pe lângă x minus primar rădăcină
pe lângă x minus y rădăcină practic
minus minus adică plus x la a treia
plus x pătrat plus x plus unu se
va scrie ca x plus 1 pe lângă x
minus y pe lângă x plus y dacă
luăm și discutăm numitorul x la
a treia plus 1 minus x pătrat minus
va fi egal cu x factor comun pe
lângă x pătrat plus 1 minus x minus
gradul al doilea mâncat suma x
1 plus x 2 este minus b supra ceea
ce înseamnă de fapt că e minus
1 minus x supra 1 adică e minus
1 minus în fața unei fracții sau
unei paranteze schimbat semne tuturor
termenilor din paranteză respectiv
produsul x 1 x 2 egal cu c supra
a ceea ce înseamnă de fapt sunt
Noni titlul este minus x supra
1 practic minus în aceste condiții
Este evident că X1 este minus 1
x 2 este practic minus 1 ori îmi
dă minus respectiv minus 1 plus
Cine e ministrul astfel x la a
treia plus 1 minus x pătrat minus
x este egal cu x pe lângă x minus
ma rădăcină pe lângă x minus a
doua rădăcini se obține aspect
x pe lângă x minus y pe lângă x
plus Revenim la stația de simplificat
și completăm ceea ce Noi am de
terminat un discuția anterioară
astfel x la a treia plus x pătrat
plus x plus 1 supra x la a treia
plus 1 minus x pătrat minus X egal
cu x plus 1 pe lângă x minus y
pe lângă x plus y supra x pe lângă
x minus pe lângă x plus 1 în mod
Evident x plus unu se reduce cu
x plus 1 x minus se duce cu x i
astfel rezultatul fracției după
simplificare este x plus y supra
x după parcurgerea exemplelor de
mai sus necesară exprimarea ecuațiilor
de gradul al doilea pornind de
la rădăcini astfel ecuația x pătrat
plus bx plus c egal 0 cu a diferit
de 0 se poate scrie printer produsului
rădăcinilor a x pătrat minus x
plus p egal cu 0 formă pe care
deja o cunoșteam în momentul în
care discutăm despre ecuații de
gradul al doilea cu rădăcini real
așa cum știam este excuses 2 pe
1 este x 1 înmulțit cu x 2 Dacă
toate sunt complexe Asta este situația
pe care o comentăm acum admitem
că X1 ar fi m plus n e casă în
care install fără doar și poate
va fi m minus n e conjugatul lui
În condițiile astea îs urcare X1
procesului va fi pentru sanie plus
a minus n e practică in equalizer
obținând rusească suma ca fiind
2 m p este egal cu x 1 x 2 adică
pe lângă mine ce ce ce înseamnă
m pătrat plus pătrat x pătrat minus
x plus b egal cu 0 este ecuația
de gradul al doilea raportată la
sumă și produs moment În care În
condițiile date ecuația de gradul
al doilea va fi x pătrat minus
2 m x plus m pătrat pătrat egal
cu zer practică în cazul în care
o ecuație de gradul al doilea are
soluții complexe vom obține suma
dublul părțile ale soluțiilor iar
produsul va fi constituit din suma
pătratelor părții reale respectiv
părți imagina exemplu X1 egal cu
2 plus 3x 2 egal cu 2 minus 3 suma
sa fie 4 produsul egal cu 2 la
a doua plus 3 la a doua produsul
este 4 plus 9013 ecuația de gradul
al doilea căutată este XP minus
4x plus 13 egal 0

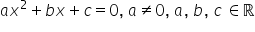
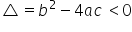
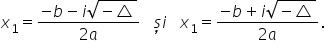
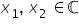 sunt soluțiile complexe ale unei ecuații de gradul doi, atunci ecuația va avea forma:
sunt soluțiile complexe ale unei ecuații de gradul doi, atunci ecuația va avea forma: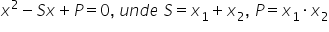
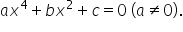
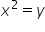 și obținem o ecuație de gradul doi:
și obținem o ecuație de gradul doi: 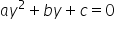 cu soluțiile
cu soluțiile