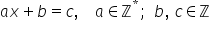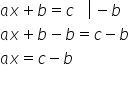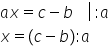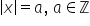Ecuații în Z

A rezolva o ecuație înseamnă găsit

soluția sau mulțimea soluțiilor

sale soluțiile unei ecuații sunt

acele valori ale variabilei pentru

care egalitatea este adevărată

o să încep cu ecuație mai simplă

x plus minus 2 egal cu minus 3

unde x este un număr întreg bristo

separăm necunoscuta x de ceilalți

termeni a ecuației asta avem în

membrul stâng Doamne cunoscuta

x 4 y să adunăm opusul numărului

minus doi deoarece atunci când

adunăm unui număr opusul său Rezultatul

este zero așa dar o să adunăm numărul

2 în ambii membri ai Egalității

și obține x plus minus 2 plus 2

egal cu minus 3 plus 2 minus 2

plus 2 este 0 și obținem x egal

minus trei plus doi este minus

unu soluția acestei ecuații este

numărul întreg minus 1 a doua ecuație

x minus 5 egal cu minus 1 ca să

rămână în membrul stâng necunoscuta

x trebuie să adunăm numărul 5 la

ambii membri ai Egalității și obținem

x minus 5 plus 5 egal cu minus

1 plus 5 minus 5 plus 5 este 0

deoarece sunt numere opuse și obținem

x egal cu 4 soluția acestei ecuații

este numărul întreg 4 a treia ecuație

2x plus 3 egal cu minus 15 mai

întâi să eliminăm numărul 3 din

membru stang iar pentru aceasta

va trebui să scădem numărul 3 din

ambii membri ai ecuației și obținem

2x plus 3 minus 3 nu o să mai scriu

deoarece este 0 egal cu minus 15

minus trei 2x va fi egal cu minus

18 asta eliminăm coeficientul 2

din fața necunoscutei x va trebui

să împărțim această ecuație la

2 între 2 și x fiind înmulțire

operația inversă înmulțirii este

împărțirea și atunci în membrul

stâng rămâne necunoscuta x are

va fi egală cu minus 18 împărțit

la 2 adică x va fi egal cu minus

9 soluția este numărul minus 9

a patra ecuație 5x plus 3x egal

cu minus 16 Un alcan necunoscut

IX apare de două ori în această

ecuație scopul este să reducem

termenii care conțin necunoscuta

x la un singur termen să vedem

cum putem să adunăm 5x cu 3X deoarece

x apare ca Factor în ambii termeni

putem să dăm pe X factor comun

și obținem x pe lângă 5 plus 3

egal cu minus 16 adică x ori 8

egal cu minus 16 înmulțirea este

comutativă și putem scrie 8 x egal

cu minus 16 această etapă se poate

emite în general Și atunci când

trebuie să adunăm doi termeni care

conțin aceiași necunoscută vom

aduna cu eficienți lor același

lucru este valabil și pentru scădere

Așadar 5 x plus 3 x este 8 x asta

eliminăm coeficientul 8 va trebui

să împărțim la 8 ambii membri și

obținem x egal cu minus 16 împărțit

la 8 Adică x egal cu minus 2 soluția

este numărul minus 2 a cincea ecuație

2 pe lângă x plus 4 egal cu minus

12 mai cheama folosind distributivitatea

înmulțirii față de adunare și ca

să desfacem această paranteză trebuie

să înmulțim numărul 2 cu fiecare

număr din paranteza și obținem

2x plus 8 egal cu minus 12 scădem

numărul 8 din fiecare membru și

obținem 2x egal cu minus 12 minus

8 2x va fi egal cu minus 20 împărțim

la doi și obținem x egal cu minus

10 soluția acestei ecuații este

numărul minus 10 așa se ecuație

valoarea absolută a numărului x

este egală cu 3 numerele întregi

care au valoarea absolută egală

cu trei sunt minus trei și trei

vrea amintesc că modulul sau valoarea

absolută a unui număr întreg este

distanța de la origine până la

acel număr pe axa numerelor și

atunci Putem să scriem direct soluția

aceasta va fi formată din numerele

întregi minus trei și trei și ultima

ecuație valoarea absolută a lui

x minus 2 este egală cu 5 numerele

întregi care au valoarea absolută

egală cu cinci sunt minus cinci

și cinci Și atunci aveam două variante

x minus doi poate să fie egal cu

minus cinci sau x minus doi poate

să fie egal cu 5 o să mai scriu

o dată prima ecuație x minus 2

egal cu minus 5 asta eliminăm numărul

minus 2 din membrul stâng va trebui

să adunăm opusul sau și obținem

x egal cu minus 5 plus 2 adică

x egal cu minus 3 această aș fi

o posibilitate să rezolvăm acum

a doua ecuație o să mai scrii o

dată x minus 2 egal cu 5 la fel

adunăm opusul lui 2 și obținem

x egal cu 5 plus 2 x egal cu 7

aceasta ar fi a doua posibilitate

și atunci Putem să scriem soluția

is va fi formată din ținea numerelor

minus 3 și 7