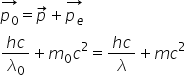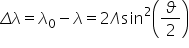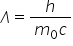Efectul Compton. Calculul variaţiei lungimii de undă.

În ciuda treia lecție de fizică

cuantică vom discuta despre efectul

compton în lecțiile precedente

Am văzut cum efectul fotoelectric

extern a forțat lumea fizicii Să

accepte un nou tip de realitate

un alt tip de model pentru radiația

electromagnetică și anume comportarea

corpusculară aragaz electromagnetice

și a luminii în particular efectul

compton și experimentul contin

a convins savanții oamenii de știință

că această comportare corpusculară

a luminii și a radiației tot mai

mici în general este corect deci

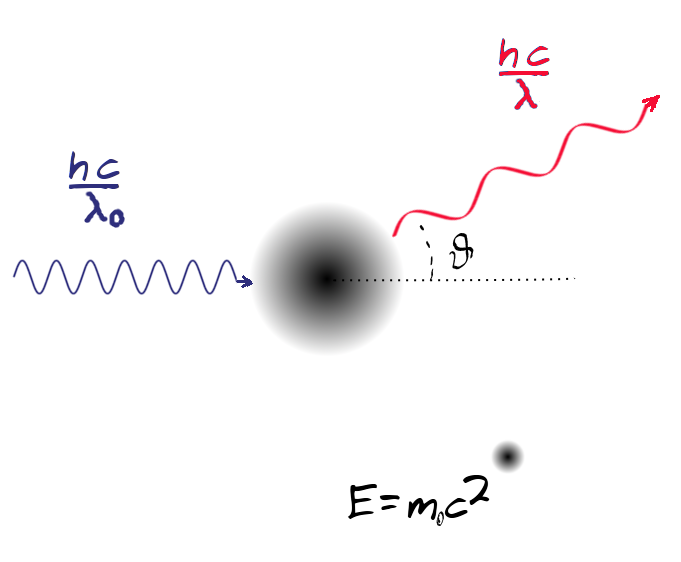
să începem cu descrierea întru

forma simplificata experimentului

contin Deci avem o sursă de radiație

monocromatică cu frecvență mare

adică Oradea ție X sau gama mici

avem o anumită sursă s care emite

această radiație electromagnetică

de tip X sau gama deci de frecvență

mare și acest fascicul îngust de

fotoni va trece prin tu un bloc

de material cu atomii ușor Spre

exemplu grafit și parafină se va

împrăștia în interiorul acestui

material pe atomi materialului

și va rezulta o radiație x sau

gama împrăștiat Deci obținem Toto

radiația electromagnetică împrăștiat

notăm cu Lambda 0 lungimea de undă

a radiației incidente și cu Lambda

lungimea de undă a radiației împrăștiate

De ce se folosesc atomizor e motivul

este simplu electronii atomilor

ușor sunt slab legați de nuclee

lor și pot fi considerați aproximativ

liberi radiația incidentă se va

împrăștia deci pe acest electroni

aproximativ liberi Ce înseamnă

asta pur și simplu că electro Cum

se mișcă în atom în jurul unui

nucleu a cărui sarcină este plus

Și de ce avem un electron în mișcare

în jurul dacă z este mic adică

numărul de protoni care au sarcină

1 și se află nucleu numărul de

protoni este mic atunci forța de

atracție a electronului față de

nucleu este mică și atunci intră

Buna aproximație putem considera

electroni liber pentru că avem

nevoie de o energie mică în caz

acesta pentru a desprinde electronul

din atomul sau dacă este mic și

Deci pentru atomii ușor putem aproxima

electronul ca fiind liber dorim

să măsurăm variația lungimii de

undă între radiația emergentă sau

împrăștiată Lambda și cea incidentă

Lambda 0 Îți dorim să măsurăm acest

Delta la am dat definit calendar

minus la 0 Deci situația schematică

arată în felul următor în starea

inițială avem un Foton Care este

incident pe un electron care se

află în repaus și este liber între

aproximație bună în cazul acestor

tipuri de atun energia fotonului

0 este h10 iar impulsul fotonului

este h10 împărțit la c aceasta

deoarece în cazul unui Foton putem

scriu următoarele ecuații egal

cu MC pătrat aceasta este ecuație

pentru orice tip de particulă dar

în particular pentru foto nu avem

impulse egal cu MC bineînțeles

impulsul în general este m dar

fotonul are întotdeauna viteza

si și Deci impulsul fotonului este

mc de aici rezultă că relația dintre

energie și Impuls pentru foto nu

mai este egal cu pe orice Deci

putem scrie pe 0 egal cu 0 împărțit

la c în starea finală bineînțeles

vom obține un Foton împrăștiat

care va avea o energie e egal cu

H 1 și un Impuls pe egal cu h n

împărțit la c și un electroni și

el împrăștiat nici electronul va

avea o energie a electronului m

c pătrat relația Einstein sau ecuația

niște și un Impuls pe e egal cu

m v nu mai putem scrie energia

electronii împărțită la ce această

relație este adevărată doar pentru

foto și Deci avem aceste relații

între starea inițială și starea

finală a împrăștierii fotonului

pe electron și vom aplica conservarea

impulsului și a energiei în forma

lor relativă stă pentru că atât

furtunul cât și electronul când

se află în mișcare au viteze comparabile

cu viteza luminii pentru a calcula

acest Delta la Deci pornim cu conservare

impus Cum sărim pulsului se scrie

simplu impulsul fotonului în starea

inițială în principiu ar trebui

să scriem plus impulse electronului

Dar el se află în repaus și e De

ce este 0 egal cu impulsul final

Care este suma dintre impulsul

fotonului în starea finală plus

impulsul electronului după împrăștiere

ca să Reprezentăm această vectorială

această ecuație avem ceva de genul

acesta impulsul pe zero al fotonului

starea inițială va fi suma dintre

impulsul fotonului în starea finală

și impulsul electronului în starea

finală notăm cu un cu teta unghiul

dintre direcția fotonului în starea

finală și starea inițială Deci

teta este unghiul de împrăștiere

al fotonului și să notăm cu alfa

unghiul de la Vârful acestui triunghi

este dai imediat de ce putem scrie

imediat relația care leagă mărimi

magnitudine les au mărimile celor

trei impulsuri și anume pe e pătrat

este egal cu psd.ro pătrat plus

b pătrat minus 2 pe înmulțit cu

0 cosinus de tura de aici putem

scrie explicit impulsului putem

înlocui explicit valorile impulsurilor

și anume după cum e sus impulsul

electronul este egal cu m w impulsul

inițial al fotonului pe zero este

h10 împărțit la c și impulsul final

al fotonului este h n împărțit

la c înlocuire obținem următoarea

ecuație m z m pătrat de pătrat

ce pătrat si pătrată apare datorită

faptului că înmulțim ecuația Cu

ce păcat Deci acest si pătrat de

la numitor îl aducem o față și

de ce obține m pătrat de pătrat

c pătrat este egal cu pe 0 la pătrat

rămâne aș pătrat ne 0 pătrat D

pătrat rămâne H pătrat nu pătrat

minus 2 H pătrat minus zero cosinus

de pi și acum trecem la conservarea

energiei conservarea energiei se

scrie în felul următor energia

fotonului în starea inițială în

h10 plus energia electronului în

stare Inițială care se află în

repaus Deci va fiind doar energia

de repaus a electronului și anume

masa de repaus electroni în 0 mulți

Vita cu ce va fi egală cu energia

final după împrăștiere care este

H1 energia fotonului plus Mc pătrat

de data aceasta masa electronului

va fi masa de mișcare pentru că

electronul după împrăștiere se

mișca ca și comentariu dacă atomul

ar fi fost un atom greu și atunci

forța de interacțiune dintre electroni

și nucleu nu mai poate fi neglijată

nu mai putem lucra în aproximație

electronilor liberi atunci această

conservarea energiei ar fi trebuit

să conțină și un lucru mecanic

de extracție Deci mai existe un

termen energetic care este lucrul

mecanic de extracție a electronului

din atomul în care el este legat

dar din nou în cazul atomilor ușori

acest lucru lucru de mecanic de

extracție este foarte mic comparat

cu celelalte energii va reamintesc

din nou că Spre exemplu energia

fotonului este foarte mare ne aflăm

în domeniul radiațiilor X sau gama

nu 0 și nu sunt mari Deci putem

neglija pentru atomii ușor acestea

scriem această ecuație în felul

următor m c pătrat este egal cu

h n 0 minus h n plus m 0 si pătrat

și eu ridicăm la pătrat obținând

următoarea ecuație Deci ridicând

această ecuație la pătrat obținem

m pătrat și la patra apoi suma

pătratelor fiecărui termen Deci

h10 pătrați plus H pătrați scuzați

H pătrați 0 pătrat plus pătrat

nu pătrat plus m0 pătratice la

patra acestea sunt pătratele celor

trei termeni și apoi combinații

de tipul 2 a b Deci Haideți să

scriu undeva mai sus ecuația generală

ar fi a plus sau ide să scriem

Cum este a minus b plus c la pătrat

este egal cu a pătrat plus b pătrat

plus c pătrat minus 2 a b minus

2 b c plus 2-a și în felul acesta

obținem această ecuație Haideți

să le scădem Deci scădem din această

ecuație ecuație obținută din conservare

impulsuri adică aceasta scădem

aceasta această ecuație minus această

ecuație și obținem m pătrați ce

pătrați înmulțit cu ce pătrat minus

V pe frați din partea stângă a

celor Două ecuații din partea dreaptă

observăm că avem câteva simplificări

acesta se simplifice stat chesterman

se simplifică cu acesta obținem

în continuare m0 pătrați c la a

patra apoi din acești doi termeni

putem scrie 2h pătrați Nu nu 0

înmulțit cu 1 minus cosinus de

tot de aici în rămâne 1 Și de aici

rămâne un consens de tratat de

chin aceeași grupe în acest doi

termeni obținem acest termen și

apoi ne mai rămân în sfârșit acești

doi termeni din cele două ecuație

din conservare în Egipt care le

scriem în forma următoare 2 h mulți

cu nu 0 minus nu am 0 c 4 în Următorul

pas vom demonstra că de fapt acești

doi termeni sunt egali acestor

acest termen este egal cu acest

termen și poți Simplificați pentru

aceasta plecăm de la Ecuația relativista

a masei și anume că masa întru

sistem de referință inerțială este

egală cu gama înmulțită cu masa

de repaus sau masa sistemul de

referință Problem zero gama vă

reamintiți era definit ca 1 împărțit

la radical din 1 minute pătrat

pe ce pătrat deci putem Rescrie

km 0 este egal cu m ori radical

din 1 m pătrat pe ce pătrat ridicăm

la pătrat și aducem si pătrat în

față și obține m 0 pătrat înmulțit

cu acest si pătrat va fi egal cu

m pătrat înmulțit cu c pătrat minus

b pătrat pe care ecuație cu mulțimi

Deci ultimul pas este înmulțit

cu c pătrat și atunci observăm

că obținem m0 pătrat c la a patra

adică acest termen este egal cu

m pătrat pătrat mulți cu cel pătrate

pătrate adică acestor în concluzie

putem simplifica acest termen cu

acestea Ce Ce înseamnă putem scrie

mai simplificăm Deci rămânem cu

acești doi termeni aici și putem

simplifica din nou cu 2h avem un

termen comune 2hp simplificăm judeci

obținem că h110 munții cu 1 minus

cosinus de tata este egal cu 1

0 minus nu am 0 c pătrat împărțim

la acest an 0 c pătrat și obținem

h110 împărțit la m 0 c scuzați

împărțit la 0 cm 0 cm 0 si munții

cu 1 minus cosinus de atâta va

fi egal cu unt si care rămâne înmulțit

cu 0 minus 1 Deci aceasta este

ultima ecuație care am de dus om

în pasul următor folosim identitatea

1 minus cosinus de 3 este egal

cu 2 sinus pătrat de tapet 2 și

Deci avem hg10 împărțit la m 0

c munți cu 2 sinus pătrat de tata

pe Doina Aceasta este o identitate

trigonometrică Deci acest factor

este egal cu acest Factor din trigonometrie

egal cu c n 0 minus în ultimul

pas al demonstrației împărțim prin

produsul 0 nu deci Sau dacă vreți

înmulțim cu 1 pe musical.ly cu

ați și atunci obținem 2h împărțit

la 0 5 de se simplifică aici înmulțit

cu sinus pătrat de 3 pe 2 egal

cu c împărțit la minus c împărțit

la newsin această emoție și apoi

folosim definiția lungimii de unde

vor aduc aminte lungimea de undă

era egal cu viteza înmulțită cu

perioada definiția generală În

cazul unui Foton viteza este c

SC ori te adică ce împărțit la

frecvență Deci ce învăț la frecvență

pentru în este lungimea de unt

Ce Ce înseamnă că Lambda minus

Lambda zero este egal cu 2 HP învăț

la în zero ce simt pătrat de tapet

2 aceasta este după o demonstrație

destul de laborioasă ecuația care

o doream și anume pentru Delta

Lunga prin definiția acesta este

Delta lemne de variația de lungime

de undă a fotonului în procesul

de împrăștiere a electronul unui

atom ușor va fi egală cu 2 ori

un factor Lambda sinus pătrat de

tapet doi unu de acest la am Da

bineînțeles este definit ca H împărțit

la m0 Constanța planck împărțită

la masa electronii muncită cu viteza

luminii în vid se numește lungimea

de undă compton în cazul particular

al unui electron m0 este are această

valoare și deci putem calcula direcții

lungimea de undă compton electronului

ca fiind 2 picometri proprietatea

cea mai importantă Ce rezultă din

această ecuație este că Delta Lambda

este mai mare sau egal cu 0 Deci

avem o mărime pozitivă la lungimea

de undă compton este pozitiv definită

mata cu un sincer la pătrat care

este și el pozitiv Deci Delta este

mai mare sau egal cu Z Asta este

acest fapt este este însă efectului

cont și anume variația lungimii

de undă crește continuu de de la

valoarea minimă 0 pentru tata egal

cu 0 la TT egal cu zero Adică împrăștiere

înainte a fotonului sinus de tot

am pățit la 2:00 este sinus de

0 care e 0 judeci obținem Delta

la zero și apoi acrește până la

valoarea maximă care are loc la

pentru un tată egal cu 180 de grade

deja 180 de grade tata pe 2 de

vin 90 de grade când sinus de vine

sinusul acestui unde vine unul

Deci valoarea maximă a lui Delta

la mdam este 2 la electron care

are loc la lungimea de undă compton

electronic care are loc la împrăștierea

înapoi a fotonului deci Delta la

amenda este mai mare sau egal cu

0 egal cu 0 pentru tata egal cu

0 și maxime pentru teta egal cu

180 efectul compton este această

apariție a radiațiilor emergente

cu lungime de unda mai mare decât

a radiațiilor incidente la împrăștierea

razelor x a gama întors Tanța cu

atomi ușori deci de asta am dar

care este la minus lan de zero

este mai mare sau egal cu 0 asta

implică bineînțeles kalenda în

efectul compton este mai mare sau

egal cu lemn de 0 Acesta este un

fapt esențial deoarece în modelul

modelul ondulator al luminii nu

putem avea un astfel de efect întru

model ondulatorul al acestui tip

de interacțiune Lambda trebuie

să fie egal cu 0 indiferent de

valoarea unghiului teta sau a altor

parametri Maxxis se întâmplă între

accent.ro modelare cu ajutorul

modelul ondulatoriu am avea radiația

care ar interacționat cu electronul

lar pune pe acesta pe electron

în mișcare oscilatorie de frecvență

egală cu 1 0 și când energia transferată

de Foton electronului aflat în

această mișcare oscilatorie suficientă

pentru a rupe din atom acest electroni

se va desprinde și va ieși din

material radiația împrăștiată având

și ea tot valoarea nu 0 Deci întru

modelul Andu la toriu Delta laudam

este egal cu 0 sau dacă ținem cont

de faptul că electronul are o interacție

cu nucleul său ar putea adică aceste

obții induse ale electronului induse

de către fotonul incident sunt

amortizate atunci acest Delta lom

dar poate scădea ușor dar nici

un caz întru model ondulatoriu

nu putem avea o creștere substanțială

a lui Lambda după împrăștiere Deci

modelul ondulatoriu eșuează fundamental

în explica rezultatele experimentului

contin pe când după cum vedem din

toată această Demonstrați modelul

corpuscular al radeti electromagnetice

verifică sau Explică foarte ușor

rezultatele experimentale care

sunt în concordanță cu aceste formule