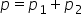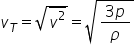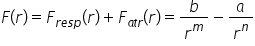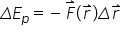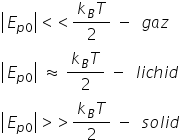Extinderea modelului gazului ideal. Stările de agregare.

încet da șaptea lecție de termodinamică

vom continua și termina discuția

noastră despre teoria cinetico

moleculara să luăm în discuție

o aplicație practică a am dori

cinetică moleculare și anume legea

dalton din termodinamic în particular

Să considerăm două gaze amestecate

care formează un sistem termodinamic

energia cinetică medie a amestecului

de gaze va fi prin definiție Digi

Energy cinetică medie prin definiție

sta întotdeauna suma tuturor energiilor

cinetice ale moleculelor sau atomilor

din substanță unde deci în este

numărul total de molecule din provenind

din cele două gaze mestecat împărțită

la numărul de molecule aceste definiția

valorii medii a oricărei parametrul

în particular în acest caz energia

cinetică a unei molecule dar gazul

nostru este format din amestecul

de două gaze Deci numărul total

de molecule va fi egal cu suma

am numărul de molecule individual

Deci energia cinetică medie va

avea această formulă despărțită

în mele pe negi cinetice ale celor

două gaze ce formează amestecul

în continuare această relație poate

fi scrisă în felul următor unde

am folosit ecuația pentru energia

cinetică a unui atom sau moleculă

energia cinetică este masa ori

viteza la pătrat împărțit la 2

toate moleculele de același tip

au aceeași masă Deci toate moleculele

de tipul 1 vor avea masa m-1 toate

moleculele de tipul 2 va avea masa

im2 dar vitezele lor bineînțeles

vor știi diferite toată molecule

au viteze diferite între ele în

concluzie sub ma se scrie în felul

următor și bineînțeles din definiția

mediei unui parametru din nou De

ce aplicăm aceeași definiție ca

acea pentru mediane cinetice dar

în acest caz pentru viteza la pătrat

și atunci putem scrie că energia

cinetică medie este unul pe an

1 plus 2 înmulțit cu 1 pe 2 iar

această sumă va deveni în 1 înmulțit

cu Vita media vitezei la pătrat

a moleculelor de tipul 1 Deci din

nou am folosit faptul că în acest

caz media viteze la pătrat prin

definiție este 1 supra n sumă din

z pătrați cu e de la 1 la ea și

obținem această ecuație apoi putem

folosim ecuația generală pentru

energia cinetică medie Care este

3 pe 2 Constanța boltzmann ore

temperatura aceasta este valabilă

pentru orice tip de caz această

ecuație poate fi scrisă ca 3 pe

2 Constanța universală a gazelor

mulți tool cu temperatura împărțită

la numărul lui avocatul această

din definiția constantei boltzmann

și mai departe folosind ecuația

generală a gazelor putem scrie

Acest această cantitate ca 3 pe

2 înmulțită cu produsul dintre

presiune și volum împărțită la

numărul de kilomoli înmulțit cu

numărul e avocat din nou această

rezultă din ecuația generală acasă

care spune că pev este egal cu

n u r t și în final putem scrie

ecuația cinetică medie a unei molecule

ca fiind 3 pe 2 pe V împărțit la

numărul total de molecule în numărul

de kilomoli înmulțit cu numărul

lui avogadro prin definiție este

n care este în unu plus în doi

din aceste Două ecuații obținem

că 3 pe 2 TV este egal cu 1 pe

2 înmulțit cu M1 n1 Z1 pătrat medium

plus m2n 2 v-2 pătrat meciul în

singur lucru ca la făcut în acest

pas a fost să simplificăm unul

pe an 1 plus N2 care e prezent

în ambele părți ale egalități rezultă

imediat că TV sau mai exact pe

direct presiunea deci putem simplifica

doar un și obține un 1 pe 3 iar

în paranteză Trebuie doar să mai

împărțim cu volumul iar numărul

n 1 împărțit la Z vada in unul

mic densitatea sau numărul de molecule

pe unitatea de volum de ce avem

in 1 m 1 v-1 pătrat mediu plus

m2 m2 V2 pătrat meci în concluzie

am demonstrat că pe presiunea totală

este egală cu presiunea parțială

a gazului 1 plus presiunea parțială

a gazului 2 acestea sunt 1 pe 3

in 1 m 1 v-1 pătrat mediu este

exact pe 1 din ecuația fundamentală

a teoriei cinetico moleculare în

concluzie am demonstrat legea dalton

care în forma ei din termodinamică

este ca și orice lege de termodinamică

stabilită experimental care spune

că intru în amestec de două case

presiunea totală egală cu suma

presiunilor parțiale exercitate

de fiecare componentă gazoasă în

parte independent de prezenta celorlalte

numai că noi în cadrul teoriei

cinetică moleculare am demonstrat

o matematică aceasta este valabil

cu toate sau pentru toate legile

termodinamicii sunt demonstrat

experimental în termodinamică dar

sunt demonstrat a Teoretic în fizica

statistică teoria cine de comori

fiind un caz de particular al fizicii

statistice alt subiect este legat

de m așa numita viteză termică

a gazului din ecuația fundamentală

a termodinamicii știind că pe este

egal cu 1 pe 3 din înmulțită cu

densitatea gazului înmulțită cu

viteza medie a pătratului viteze

de aici rezultă că radical din

Media pătratului vitezei va fi

radical din de triplul presiunii

împărțit la densitate această cantitate

se numește viteză termică a gazului

iar întradevăr unități de metru

pe secundă și de o estimează de

o cuantificare a gradului de agitație

termică prezentă în casă Interesant

este dacă calculăm această cantitate

această viteză termică pentru un

gaz de hidrogen aflat în condiții

normale Adică o presiune presiunea

egală cu o atmosferă Care este

10 la a cincea Pascal și temperatura

de 273 grade Kelvin adică 0 grade

Celsius putem măsura pentru acest

gaz în aceste condiții de presiune

și temperatură Care este densitatea

și obținem această valoare înlocuind

acești parametri în ecuația vitezei

termice obținem o viteză termică

surprinzător de mare și anume de

1 km pe secundă aceasta este viteza

moleculelor de hidrogen în condiții

normale de temperatură și presiune

aia inițial a fost considerată

greu de crezut și considerată un

test alte oricine Tico moleculare

până când întradevăr în 1920 a

fost măsura experimental și verificată

că între adevăr este atât de mare

în concluzie teoria genetică moleculară

și modelul de la baza a Care este

modelul gazului ideal a fost verificat

destul de extensiv și sa tras concluzia

că este un model bun Întrebarea

este Până la ce punct presupunerile

cele patru presupuneri sau ipoteze

care stau la baza ideal sunt corecte

realitate Deci întrebarea se pune

în ce caz este necesar să extindem

acest model la gazul ideal pentru

al face corect în realitate asta

din moment ce am văzut că în multe

cazuri el întradevăr funcționează

un prim răspuns la în văzut de

așa și anume În cazul în care moleculele

sau atomi au dimensiuni neglijabile

bună din presupunere la că dimensiunile

atomului sau un particulara molecule

pentru că ele sunt mai mari sunt

neglijabile da bineînțeles să avem

în multe situații avem de a face

cu molecule suficient de mari ca

această presupunere să nu mai fie

corectăm și în acest caz prima

extindere a modelului gaz ideal

este considerarea unui număr de

grade de libertate mai mare decât

3 va duc aminte numărul de grade

de libertate e este egal cu 3 dacă

considerat numai coordonatele de

translație ale mișcării x y și

z totuși dacă molecula e suficient

de mare atunci iar și alte mișcări

în interiorul gazului decât translația

Spre exemplu se poate roti in jurul

axei proprii deci putem considera

Spre exemplu rotația moleculelor

iar pentru anumite de rotație și

anume cea cu o axă rigidă cu cu

distanța dintre atomii molecule

lichide e va fi egal cu 5 putem

considera și alte tipuri de mișcări

ale moleculei și atunci trebuie

să creștem acest grad de libertate

acest număr de libertate În consecință

o extensie mai semnificativă a

modelul gazului de el are legătură

cu distanța dintre molecule Dacă

vă duceți aminte un o altă presupunere

din modelul gazului de el era că

distanța dintre molecule este mult

mai mare decât dimensiunea moleculă

Evident în pentru gazele aflate

la presiune joasă aceasta este

adevărat dar odată ce crește presiunea

gazului și cu atât mai mult o dată

și Considerăm lichide sau solide

atunci distanța dintre molecule

de vine comparabilă cu dimensiunea

moleculelor Care este de ordinul

unui nanometru Neciu nanometru

este nanometru este de ordinul

10 la minus 9 metri în acest caz

nu mai putem considera că nu există

interacțiuni între molecule Deci

în acest caz trebuie să introducem

să extindem modelul cazului introducând

forțe de interacție dintre molecule

aceste forțe de interacție au fost

măsurate și calculate ele sunt

destul de complexa vând atât o

componentă repulsivă de respingere

f r cât și o componentă de atractiv

de atracție f a forma lor generală

este invers proporțională cu o

putere a distanței și bineînțeles

semnul forței este dat de tipul

a o forță atractivă este negativă

o forță Eva este pozitiv ca să

Reprezentăm grafic rezultă că Forțele

de interacțiune molecule au această

formă generală Deci forța ca funcție

de distanță distanța intra moleculară

Deci iar un minim și apoi timp

de către 0 Cele două componente

ale ei fiind una repulsiv aceasta

acesta este f r și una atractivă

Care este negativ a câteva comentarii

observăm că la distanțe foarte

mici forța repulsivă domină și

Deci moleculele se resping la distanțe

mari forța atractivă domină și

atunci molecule încep să se tragă

Există o distanță pe care o notăm

cu 0 în care cele două devin comparabile

și forța are un caracter mai complex

acest această forță care este de

natură electromagnetică este o

forță conservativă aceasta dacă

va duceti aminte din lecția de

dinamică în care am discutat forțe

conservativ a înseamnă că variația

energiei potențiale este egală

cu lucrul mecanic de ce este egal

cu produsul dintre Forța F din

intra moleculară și deplasare a

produse de ea aceasta înseamnă

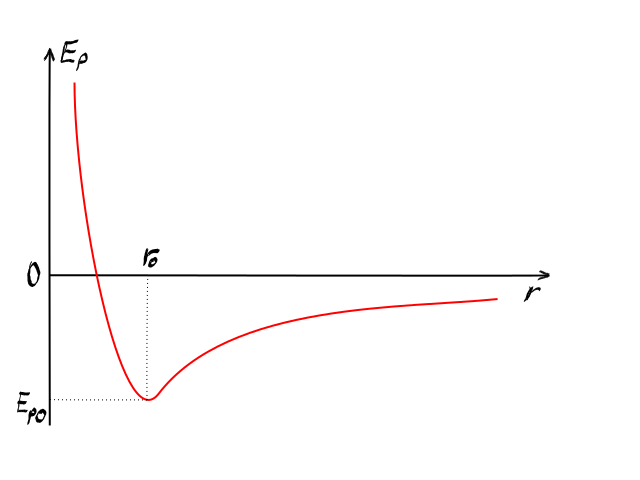
că energia potențială va avea o

formă similară cu forța de ce energia

potențială ca funcție de distanța

intra moleculară va avea și ia

un minim și apoi va tinde către

0 minimul se află la aceeași poziție

0 și îl notăm acest minim cu e

pe 0 Deci e pe 0 este dacă vreți

adâncime aceste gropi faptul că

există o asemenea groapă de potențial

adică energia potențială are această

regiune pe care o înconjoară acum

este foarte semnificativ pentru

că se demonstrează că prezența

unei anumite gropi de potențial

ca aceasta duce la stări legate

asta înseamnă că dacă energia cinetică

a moleculelor este comparabilă

cu mărimea acestei gropi adică

cu e pe 0 atunci moleculele care

se află la distanțe compara 0 nu

mai sunt libere libere ce sunt

legate între ele prin forțe de

aceste forțe de interacție Deci

o groapă de potențial cu anumită

adâncime va duce la stări legate

pentru un recul se se află la distanțe

comparabile cu acest aceasta ne

permitem să devenim mult mai cantitativi

în descrierea noastră a stărilor

de agregare și să putem spune că

dacă energia cinetică a medie a

unei molecule care după cum am

văzut este habite împărțit la 2

dacă această energie cinetică medie

este mult mai mare decât energia

potențială decât minimul energiei

potențiale Dică de mărimea acestei

gropi de potențial atunci mișcarea

cinetică sau agitația termică domină

interacție din sistem moleculele

devin libere lasi lupi din aceste

legături potențiale devin libere

și atunci avem de a face cu un

gaz nici un gaz este dacă vreți

un sistem termodinamic în care

energia cinetică dată de agitația

termică domină interactive date

de Forțele de interacțiune dintre

molecule dacă în această energie

potențială groapa de potențial

adâncime a este comparabilă cu

energia cinetică medie atunci avem

o dacă vreți o luptă pe picior

de egalitate între cele două tipuri

de fenomene obținând lichid lichidul

este substanța în care moleculele

încă se pot mișca pentru că au

suficientă energie cinetică t cu

interacția de cu forța de atracție

dintre ele Deci se pot mișca dar

o pot face numai condiționat sau

constructional mișcarea lor nu

este liberă ca în cazul gazul și

ultimul caz este în care bineînțeles

energia potențială groapa adâncimea

acestei inițiale dintre Roxy este

mult mai mare decât energia cinetică

medie care vine din agitația termică

caz în care avem astfel de stările

moleculele nu se mai mișcă decât

eventual au mișcări de vibrație

dar nu mai au mișcări de translație

iar acesta este după cum știm un

solid intru stare solidă în moleculele

sau atomi se află în poziții fixe

în care ventral pat fibra în jurul

acelor poziții dar nu mai există

mișcare liberă