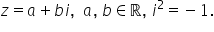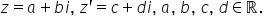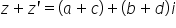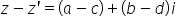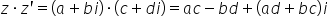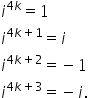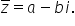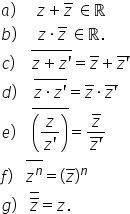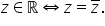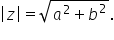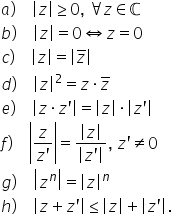Forma algebrică a numerelor complexe

această lecție se constituie ca

o continuare a lecției precedente

și anume lecția de numere complexe

în prima etapă vom comenta despre

forma algebrica numerelor complexe

notația Z egal cu Perechea ab introdusă

pentru numere complexe nu este

întocmai comodă atunci când facem

calcule cu numere complexe de aceea

în general se folosește o altă

scrierea numerelor complexe prin

convenție numărul complex 01 este

notat cu e astăzi 10 egal cu Perechea

ordonată de numere reale AB este

de fapt suma perechilor ordonate

a 0 plus 0 b a 0 b este de fapt

b0 ca perechi ordonată înmulțită

perechea ordonată 01 prin aplicarea

formulei de înmulțire învățate

în lecția precedentă se obține

0 b acest aspect a trage de la

faptul că zic ca și perechi ordonată

abe este de fapt egal cu Perechea

ordonată a 0 Da plus b 0 înmulțit

cu 0 1 Da A 0 este număr real dacă

va aduceti aminte Da amic pe 0

este numărul real d mic și 01 prin

convenție este în aceste condiții

jetul va fi egal cu a plus b e

exemplu dacă avem perechea doi

minus unu se va scrie k20 plus

0 minus unu suma perechilor ordonate

doi zero plus zero astfel doi zero

este 2 numărul real respectiv 0

1 este produsul perechilor ordonate

minus 1 0 cu 0 1 0 1 am stabilit

că este Deci perechea ordonată

doi minus unu sau numărul complex

2 minus 1 se scrie ca 2 minus în

aceeași ordine te310 se scrie ca10

plus 0 0 1 0 0 0 ori 0 110 1 plus

0 0 minus 3 se va scrie ca 0 0

plus 0 minus 3 ca pereș ordonată

zero zero Ricky automată plus 0

minus 3 scrisă ca produs de perechi

ordonate și anului minus trei zero

înmulțit cu 0 1 0 1 este Deci perechea

0 minus 3 se va scrie ca 0 minus

3 adică minus 3 numărul complex

se numește unitate imaginară și

numerele de forma b a cu b număr

real se numesc imaginar dacă numărul

complex z se scrie sub forma a

plus b y atunci a se numește parte

reală și b se numește parte imaginara

numărului complex astfel pentru

ZTE cal cu 2 plus 3 real este 2

imaginar de 10 este 3 în acest

moment operațiile algebrice prezenta

Ce poți relua adunarea z care era

perechea ordonata b este scrisă

acum apăs pe și sat prin care era

perechea ordonată Și de ce scrie

acum ca si plus te e cu evidenta

B C D aparținând lui R Deci în

condițiile acestea zi tools ab

prim va fi scris a plus b plus

c plus d a e setul sat prin va

fi a plus c plus b plus d e Dacă

aș face referire din nou la perechea

ordonată rezultat al adunării a

avea a plus c respectiv b plus

D chestionare c o știam deja în

ceea ce privește înmulțirea Space

a prim Este c plus d a e cu evidenta

b c d numere reale 10 ori prin

va fi egal cu a plus b înmulțit

cu c plus tei Astăzi a c plus a

d e plus bc plus t b i pătrat ceea

ce înseamnă a c plus b d e pătrat

respectiv a d c pe lângă e zeturi

de prin așa cum Știam ca produs

de perechi ordonate este de fapt

ace Speed pe prima poziție respectivă

ad plus BC în aceste condiții inscrierea

ca și perechi produs de perechi

ordonate respectiv ca și produs

de numere complexe scrise de forma

ab plus Ba da trebuiesc să fie

egal astfel a c plus b d e pătrat

trebuie să fie egal cu a c minus

b d respectiv a d plus PC trebuie

să fie egal cu ad plus BC este

200 al rămâne întradevăr să fie

egal ac plus b d e pătrat și a

c minus b d astfel Bet sar de duce

și e pătrat adică unitate imaginară

la pătrat va avea valoarea minusul

înțeleg astfel că puterile lui

i sau puterile numărului complex

sunt necesare în continuare pentru

calculele ce urmează a fi făcute

cu numere complexe astfel am arătat

că e pătrat este egal cu minus

1 la a treia va fi de fapt la a

doua înmulțit cu e cu mila a doua

este minus unu voi avea minciună

McQueen practic e la treia va fi

egal cu minus y la a patra este

la ei sau de ce nu e la a doua

totul la a doua 3 pentru minus

1 la puterea a doua ar fi un Deci

e la 4 egal cu a cincea e la 4:00

ori cu mina apa 301 este rezultatul

lui Ela a cincea pentru ca e la

cincea a șasea fiar minus unu E

la 7:00 e practic e la a treia

Deci minus și așa mai departe înțeleg

la masina RON că dacă n egal cu

4K ca fiind orice număr natural

Da practic 0 4 ori 2 ori 3 12 Dani

Deci 4 0 4 8 12 și așa mai departe

în acest caz va fi egal cu unu

la Deci la puterea a patra egal

cu 1 pentru n egal cu 4 ca plus

1 practic la a cincea ești la puterea

1 la puterea la puterea 5 cu 4

9 și tot așa le va fi egal cu e

în aceeași ordine de idei pentru

n egal cu 4 ca plus 2 practic pentru

e la a doua pentru e la 2:00 cu

pat la 6-a 6 cu 4 la a zecea și

așa mai departe Eli în parte minus

unu pentru egal cu patru ca plus

3 Deci pentru 3 pentru 3 cu 4 7

pentru 7 cu 411 și așa mai departe

eyeliner fie egal cu minus exemple

de aplicații pe care le puteți

întâlni când discutăm despre puterile

numărului complex Să se calculeze

suma e pătrat plus la 3:00 a patra

plus y la puterea 20 Ela a doua

murit că este egal cu a 6-a încă

din 4 în 4 se repetă la egal cu

10 egal cu e la 14:00 a respectiv

b egal cu a la 18 și egal cu minus

unu de ce Pentru că N este 4 ca

plus 2 de forma 4 ca plus 2 la

a treia este egal cu Ela șaptea

respectivii la 11:00 e la 15:00

și la 19 egal cu minus c fiind

pe situația când a nu este 4K plus

3 la 4 egal cu 8-a la 12:00 la

16:00 a luat 20 și gar cu nu suntem

pe situația Ene calcu 4K respectivi

la a cincea e la noi la a 13-a

respectivii la 17-a este e e nu

este 4K plus unu în aceste condiții

suma mea va fi egală cu S1 practic

minus 5 S 2 minus 5 plus s35 plus

s44 ISU în acest moment va fi minus

5 plus 4 minus și minus 5 plus

5 se reduc astfel suma calculată

Sau cerută să fi determinată că

avea valoarea minus în continuare

vom discuta despre numere complexe

conjugate calculați b este un număr

complex atunci numărul A minus

pe e notat cu z barat se numește

conjugatul astfel câteva exemple

ca să realizați exact ce ce vreau

să definesc mai sus practic dacă

se taie Gal cu trei plus doi e

perechea ordonată 3 2 z barat va

fi 3 minus 2 adică perechea ordonată

trei minus doi de a căzut ar fi

minus 5 minus e perechea ordonate

minus 5 minus unu z barat practic

conjugatului sat va fi minus 5

minus minus unu e în aceeași ordine

tennis 5 minus cu minus plus Deci

plus e adică perechea ordonată

minus 5 1 vedeți semn schimbat

doar pentru B la nu și pentru în

aceeași ordine de idei Dacă am

sat egal cu 4-a Praktiker au durată

04 z barat sau de conjugat va fi

minus 4 e adică 0 minus 4 Au se

copiază b își schimbase parte imaginară

schimbă semnul suma și produsul

a doua numere complexe conjugate

sunt numere reale Adică dacă am

un sat egal cu a plus b număr complex

clar Da dacă discuți despre conjugatului

vorbesc despre sat barat egal cu

oameni Îți bei În egală măsură

număr complex suma sat plus separat

sau sat plus de conjugat este a

plus b plus a minus parte reală

cu parte reală parte imaginară

cu parte imaginară adică a plus

a plus b minus pe totul pe lângă

y în acest moment Aqua 2-a minus

pe practic se reduc și interseroh

astfel Z plus z barat egal cu 2-a

dar cu aia era real În egală măsură

2-a va fi un număr când voi face

referire la produs Zetor sat barat

egal cu a plus b înmulțit cu ameninț

baie produs de sumă prin diferență

formulă de calcul prescurtat pe

care vor reamintesc că a minus

pe lângă a plus b este egal cu

a pătrat minus b pătrat astfel

că voi avea a pătrat minus 1 totul

la pătrat a pătrat minus pe pătrat

înmulțit cu e pătrat cam stat stabilit

că e pătrat este minus unu înțeleg

De fapt că se aude barat practice

turzi Conjugați este egal cu apă

3-a minus b pătrat ori minus unu

adică Zetor separat va fi a pătrat

plus b pătrat care mod Evident

aparține lui r în condițiile în

care a și b sunt numere reale determinarea

raportului dintre două numere complexe

se face utilizând conjugatul numărului

complex astăzi dacă am numărul

complex Z egal cu a plus b respectiv

numărul complex 2 egal cu c plus

d a e atunci raportul sat 1 supra

10 doi va fi a plus b supra c plus

D în mod obligatoriu se amplifică

raportul cu conjugatul numărului

complex și mai clar număr complex

de la numitor practic si plus de

e este număr complex de la numitor

conjugatul acestuia va fi c minus

de e și atunci amplifică așa cum

spuneam Cu ce minus de e înțelegând

astfel că voi obține a plus b pe

lângă c minus 3 supra așa cum am

stabilit Ce este înmulțit cu c

minus de i da Va fi si pătrat plus

b pătrat conform înmulțirii numerelor

conjugat a Da înțeleg astfel că

fac înmulțirea de la numărător

obținând astfel ace plus b supra

ce pătrat plus de pătrat practic

aceasta fiind partea reală Da deci

aparține lui ești sau nu îi spunem

real.de set 1 supra Z2 respectiv

bc minus ad supra c pătrat plus

b pătrat pe lângă aceasta fiind

imaginar de exemplu 7 minus y supra

3 plus se amplifică așa cum spuneam

cocoșul ca a ta înțeleg încă voi

amplifica cu 3 inși obținem 7 musai

pe lângă 3 minus 5 supra 3 4 8

plus 1 la pătrat astăzi 7 minus

y supra 3 plus si va fi 20 supra

10 minus 10 supra 10 modulul unui

numar complex modulul număr complex

Z egal cu a plus b se definește

ca fiind numărul real radical din

a pătrat plus b pătrat au reamintesc

partea reală a numărului complex

beul partea imaginara numărului

complex acesta se notează cu modul

de z astfel modul de z este în

realitate radical din a pătrat

plus b pătrat pentru orice sat

aparținând numerelor complexe și

definit ca a plus De exemplu dacă

îmi doresc să calculez modulul

lui unu plus trei am de fabricat

din 1 la pătrat plus 3 la pătrat

radical din 10