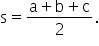Formula lui Heron (teorie)

știind că aria triunghiului se

poate afla calculând semi produsul

dintre o latură și înălțimea corespunzătoare

ei de ce Aria triunghiului este

egală cu a mic ori supra 2 în clasele

mai mici ați mai învățat o formulă

pentru aria triunghiului și anume

Produsul a două laturi ori sinusul

unghiului dintre ele supra 2 deci

aria se mai poate scrie b ori c

ori sinus de a supra 2 Dar există

situații în care nu Putem afla

înălțimea triunghiului și nu cunoaștem

nici unghiurile acestuia în aceste

situații vor folosi formula lui

Heron care ne ajută să calculăm

aria triunghiului Cunoscând lungimile

laturilor acestuia în continuare

vom de duce formula lui Heron pornind

de la această relație care se mai

poate scrie a astfel b ori c supra

2 iar în loc de sinus de a putem

să formula 2 sinus de a supra 2

ori cosinus de ape 2 aici se simplifică

2 și obținem bc ori sinus de a

supra 2 ori cosinus de ape 2 deci

am obținut relația aria este egală

cu b ori c ori sinus de a supra

2 ori cosinus de ape 2 în continuare

vom încerca să exprimăm sinus de

a supra 2 și cosinus de ape 2 în

funcție de laturile triunghiului

ABC Folosind teorema cosinusului

și avem cosinus de a este egal

cu b pătrat plus si pătrat minus

a pătrat supra 2 bc folosim de

asemenea următoarea formulăm cosinus

pătrat de ape 2 este egal cu 1

plus cosinus de a supra 2 acum

în această relație înlocuim cosinus

de a cu expresia a scris mai sus

și avem 1 plus b pătrat plus si

pătrat minus a pătrat supra 2 BC

și totul supra 2 aducem la numitor

comun și obținem 2 b c plus b pătrat

plus c pătrat minus a pătrat supra

4 b c primii trei termeni se pot

restrânge sub formă de plus c totul

la pătrat minus a pătrat supra

4 de ce descompunere expresia de

la numărător după formula a la

a doua minus b la a doua egal cu

a plus b pe lângă a minus b și

obținem b plus c plus a pe lângă

b plus c minus a totul supra 4

b c în continuare vom nota semiperimetrul

triunghiului cu s mic Deci s este

egal cu a plus b plus c supra 2

și atunci a plus b plus c este

egal cu 2 s ne propunem să exprimăm

aceste paranteze în funcție de

semiperimetrul triunghiului prima

paranteză este 2 s și acum să vedem

cum exprimăm cea de a doua paranteză

în funcție de est pentru aceasta

o să scădem din aceasta egalitate

2-a și obținem b plus c minus a

egal cu 2 pe lângă x minus A deci

a doua paranteză va fi 2 pe lângă

x minus a Așadar avem în continuare

egal cu 2 s ori 2 pe lângă x minus

a supra 4 b c egal cu esti pe lângă

x minus a supra b c am obținut

astfel cost pătrat de ape 2 egal

cu s pe lângă x minus a supra b

c prin urmare cosinus de ape doi

va fi egal cu radical din Est pe

lângă x minus a supra b c semnul

radicalului va fi plus deoarece

unghiul a supra 2 este un unghi

din primul cadran am exprimat până

acum cosinus de ape 2 în funcție

de laturile triunghiului ABC și

acum mai trebuie să exprimăm și

sinus de asupra 2 pentru aceasta

folosind formula sinus pătrat de

ape 2 este egal cu 1 minus cosinus

de a supra 2 procedăm ca și mai

sus ia în loc de cosinus de a avem

b pătrat plus certat minus a pătrat

supra 2 BC și totul supra 2 aducem

la numitor comun și avem 2 b c

minus b pătrat minus c pătrat plus

a pătrat supra 4 b c la numărător

Putem să scriem a pătrat minus

pe lângă b pătrat plus si pătrat

minus 2 b c supra 4 b c egal cu

a la a doua minus expresia din

paranteză se restrânge sub forma

b minus c totul la pătrat supra

4 b c descompunem iarăși în factori

și avem a plus b minus c pe lângă

a minus b plus c supra 4 b c în

continuare vrem să exprimăm aceste

paranteze folosind semiperimetrul

triunghiului Dacă a plus b plus

c este 2 atunci a plus b minus

c va fi 2 pe lângă x minus c iar

a minus b plus c va fi 2 pe lângă

x minus b de ce dar în continuare

cu 2 pe lângă x minus c ori 2 pe

lângă x minus b supra 4 bc egal

cu s minus si pe lângă x minus

b supra bc am obținut găsim pătrat

de ape 2 este egal cu x minus c

pe lângă este minus b supra b c

și atunci ținuți de ape doi va

fi egal cu radical din x minus

c pe lângă x minus b supra bc acum

înlocuim aceste două relații pe

care le am obținut în expresia

de mai sus voi continua aici Deci

aria este egală cu bc ori în loc

de sinus de ape doi am obținut

radical din x minus c pe lângă

a minus b supra bc iar în loc de

cosinus de ape 2 avem radical din

x pe lângă x minus a supra b c

egal în continuare cu radical din

esti pe lângă x minus a pe lângă

x minus b pe lângă x minus c unde

cu es am notat semiperimetrul triunghiului

ABC aceasta este formula lui Heron

pentru calculul ariei unui triunghi

atunci când se cunosc lungimile

laturilor acestuia